Flow Matching For Generative Modeling
一、基于流的(Flow based)生成模型
生成模型
我们先回顾一下所谓的生成任务,究竟是想要做什么事情。我们认为,世界上所有的图片,是符合某种分布 p d a t a ( x ) p_{data}(x) pdata(x) 的。当然,这个分布肯定是个极其复杂的分布。而我们有一堆图片 x 1 , x 2 , ... , x m {x_1,x_2,\dots,x_m} x1,x2,...,xm ,则可以认为是从这个分布中采样出来的 m m m 个样本。我们通过训练希望得到一个生成器网络 G G G ,该网络能够做到输入一个从正态分布 π ( z ) \pi(z) π(z) 中采样出来的 z z z ,输出一张看起来像真实世界的图片 x = G ( z ) ∼ p G ( x ) x=G(z)\sim p_G(x) x=G(z)∼pG(x) 。我们希望采样并生成出的数据分布 p G ( x ) p_G(x) pG(x) 与真实的数据分布 p d a t a ( x ) p_{data}(x) pdata(x) 越接近越好。
从概率模型的角度来看,想要做到上面说的这件事情,可以通过最大化对数似然 log p G \log p_G logpG,来优化生成器 G G G 的参数:
G ∗ = arg max G ∑ i = 1 m log p G ( x i ) G^*=\arg\max_{G}\sum_{i=1}^m\log p_G(x_i) G∗=argGmaxi=1∑mlogpG(xi)
可以证明,最大化这个对数似然,就相当于最小化生成器分布 p G ( x ) p_G(x) pG(x) 与目标分布 p d a t a ( x ) p_{data}(x) pdata(x) 的 KL散度,即让这两个分布尽量接近:
G ∗ ≈ arg min G K L ( p d a t a ∣ ∣ p G ) G^*\approx\arg\min_GKL(p_{data}||p_G) G∗≈argGminKL(pdata∣∣pG)
概率密度的变量变换定理
给定一个随机变量 z z z 及其概率密度函数 z ∼ π ( z ) z\sim\pi(z) z∼π(z) ,通过一个一对一的映射函数 f f f 构造一个新的随机变量 x = f ( z ) x=f(z) x=f(z)。如果存在逆函数 f − 1 f^{-1} f−1 满足 z = f − 1 ( x ) z=f^{-1}(x) z=f−1(x),那么新变量 x x x 的概率密度函数 p ( x ) p(x) p(x) 计算如下:
p ( x ) = π ( z ) ∣ d z d x ∣ = π ( f − 1 ( x ) ) ∣ d f − 1 d x ∣ = π ( f − 1 ( x ) ) ∣ ( f ′ − 1 ( x ) ∣ 若 z 为随机变量 p ( x ) = π ( z ) ∣ det ( d z d x ) ∣ = π ( f − 1 ( x ) ) ∣ det ( J f − 1 ) ∣ 若 z 为随机向量 p(x)=\pi(z)|\frac{dz}{dx}|=\pi (f^{-1}(x))|\frac{df^{-1}}{dx}|=\pi(f^{-1}(x))|(f'^{-1}(x)| \ \ \ \ 若z为随机变量 \\ p(\mathbf{x})=\pi(\mathbf{z})|\det(\frac{d\mathbf{z}}{d\mathbf{x}})|=\pi(f^{-1}(\mathbf{x}))|\det(\mathbf{J}_{f^{-1}})| \ \ \ \ \ 若\mathbf{z}为随机向量 p(x)=π(z)∣dxdz∣=π(f−1(x))∣dxdf−1∣=π(f−1(x))∣(f′−1(x)∣ 若z为随机变量p(x)=π(z)∣det(dxdz)∣=π(f−1(x))∣det(Jf−1)∣ 若z为随机向量
其中 det ( ⋅ ) \det(\cdot) det(⋅) 表示行列式, J \mathbf{J} J 表示雅可比矩阵,是向量函数中因变量各维度关于自变量各维度的偏导数组成的矩阵,可类比为单变量函数的导数。
流模型推导
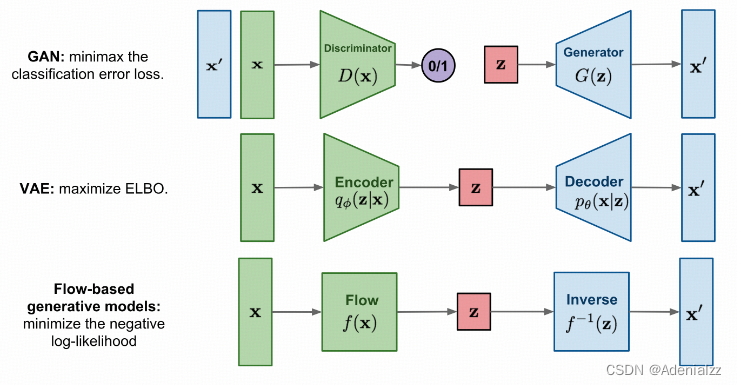
现在流行的生成模型五花八门,各显神通。VAE 优化变分下界 ELBO、GAN 通过对抗训练来隐式地逼近数据分布。流模型则可以直接优化对数似然。
流模型通过最大化对数似然,来优化生成器 G G G:
G ∗ = arg max G ∑ i = 1 m log p G ( x i ) G^*=\arg\max_{G}\sum_{i=1}^m\log p_G(x_i) G∗=argGmaxi=1∑mlogpG(xi)
而根据变量变换定理,有:
p G ( x i ) = π ( z i ) ∣ det ( J G − 1 ) ∣ , z i = G − 1 ( x i ) p_G(x_i)=\pi(z_i)|\det(J_{G^{-1}})|,\ \ \ \ z_i=G^{-1}(x_i) pG(xi)=π(zi)∣det(JG−1)∣, zi=G−1(xi)
则对数似然:
log p G ( x i ) = log π ( G − 1 ( x i ) ) + log ∣ det ( J G − 1 ) ∣ \log p_G(x_i)=\log \pi(G^{-1}(x_i))+\log |\det(J_{G^{-1}})| logpG(xi)=logπ(G−1(xi))+log∣det(JG−1)∣
要训练一个好的生成器 G G G 我们只需要训练一个(或一系列)网络完成从噪声分布 π ( z ) \pi(z) π(z) 到数据分布 p data ( x ) p_\text{data}(x) pdata(x) 的变换就可以了。在采样生成时,求出生成器的逆向网络 G − 1 G^{-1} G−1,再将随机采样的噪声输入,即可生成新的符合数据分布的样本。只要最大化上面这个式子,就可以了。
现在的问题就是怎么把这个式子算出来,具体来说,这个式子计算的关键在以下两点:
- 如何计算行列式 det ( J G ) \det(J_G) det(JG)
- 如何求逆矩阵 G − 1 G^{-1} G−1
我们设计的生成器网络 G G G 需要满足上面这两个条件,这就是流模型生成器数学上的限制。在之前的流模型研究中,研究者们提出了许多设计精巧的网络(如 decoupling layer),可以巧妙地使得网络满足上述两点便利计算的要求。
另外要提一点,流模型的输入输出的尺寸必须是一致的。这是因为如果想要 G G G 可逆,它的输入输出维度一致是一个必要条件(非方阵不可能可逆)。比如要生成 100 × 100 × 3 100\times 100\times 3 100×100×3 的图像,那输入的随机噪声也是 100 × 100 × 3 100\times 100\times 3 100×100×3 的。这与 VAE、GAN 等生成模型很不一样,这些生成模型的输入维度通常远小于输出维度。
堆叠多个网络
在实际中,由于可逆神经网络存在数学上的诸多限制,其单个网络的表达能力有限,我们一般需要堆叠多层网络来得到一个生成器,这也是 "流模型" 这个名称的由来。不过虽然堆叠了很多层,在公式上也没有什么复杂的。无非就是把一堆 G i G_i Gi 连乘起来,通过 log \log log 之后,又变成连加。
比如我们有 K K K 个网络 { f i } i = 1 K \{f_i\}_{{i=1}}^K {fi}i=1K,对噪声分布 π ( z 0 ) \pi(\mathbf{z}_0) π(z0) 进行 K K K 步变换,得到数据 x \mathbf{x} x,即有:
x = z k = f K ( f K − 1 . . . f 1 ( z 0 ) ) \mathbf{x}=\mathbf{z}k=f_K(f{K-1}...f_1(\mathbf{z}_0)) x=zk=fK(fK−1...f1(z0))
对于其中第 i i i 步有:
z i ∼ p i ( z i ) z i = f i ( z i − 1 ) , z i − 1 = f − 1 ( z i ) \mathbf{z}_i\sim p_i(\mathbf{z}i)\\ \mathbf{z}i=f_i(\mathbf{z}{i-1}),\ \ \mathbf{z}{i-1}=f^{-1}(\mathbf{z}_i) zi∼pi(zi)zi=fi(zi−1), zi−1=f−1(zi)
根据变量变换定理,相邻两步之间的隐变量分布的关系为:
p i ( z i ) = p i − 1 ( f i − 1 ( z i ) ) ∣ det J f i − 1 ∣ = p i − 1 ( z i − 1 ) ∣ det J f i ∣ − 1 \begin{align} p_i(\mathbf{z}{i})&=p{i-1}(f_i^{-1}(\mathbf{z}i))|\det\mathbf{J}{f_i^{-1}}|\\ &=p_{i-1}(\mathbf{z}{i-1})|\det\mathbf{J}{f_i}|^{-1} \end{align} pi(zi)=pi−1(fi−1(zi))∣detJfi−1∣=pi−1(zi−1)∣detJfi∣−1
每一步的对数似然为:
log p i ( z i ) = log p i − 1 ( z i − 1 ) − log ( det ( J f i ) ) \log p_i(\mathbf{z}i)=\log p{i-1}(\mathbf{z}{i-1})-\log(\det(\mathbf{J}{f_i})) logpi(zi)=logpi−1(zi−1)−log(det(Jfi))
对于整个 K K K 步的过程,对数似然为:
log p ( x ) = log p K ( z K ) = log p K − 1 ( z K − 1 ) − log ( det ( J f K ) ) = log p K − 2 ( z K − 2 ) − log ( det ( J f K − 1 ) ) − log ( det ( J f K ) ) = . . . = log π ( z 0 ) − ∑ i = 1 K log ( det ( J f i ) ) \begin{align} \log p(\mathbf{x})&=\log p_K(\mathbf{z}K)\\ &=\log p{K-1}(\mathbf{z}{K-1})-\log(\det(\mathbf{J}{f_K})) \\ &=\log p_{K-2}(\mathbf{z}{K-2})-\log(\det(\mathbf{J}{f_{K-1}}))-\log(\det(\mathbf{J}{f_K})) \\ &=\ ... \\ &=\log\pi(\mathbf{z}0)-\sum{i=1}^K\log(\det(\mathbf{J}{f_i})) \end{align} logp(x)=logpK(zK)=logpK−1(zK−1)−log(det(JfK))=logpK−2(zK−2)−log(det(JfK−1))−log(det(JfK))= ...=logπ(z0)−i=1∑Klog(det(Jfi))
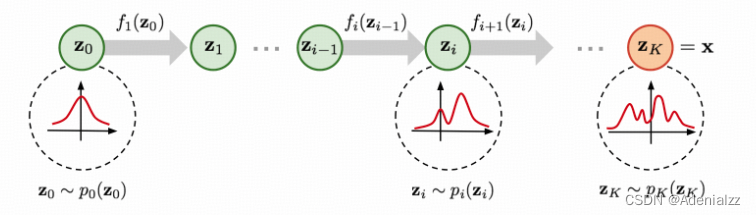
可以看到,流模型的核心思路就是通过多个可逆神经网络,一步步地将噪声分布转换为数据分布。在采样生成时,直接使用逆向网络,将随机采样的噪声样本转换为新的数据样本。
二、连续归一化流
常规流模型是在设定了离散的有限个(比如 K K K 个)可逆神经网络来逐步完成分布变换。而连续归一化流(Continuous Normalizing Flow, CNF),则是将其扩展为连续的情形。
设有 d d d 维空间中的数据 x = ( x 1 , x 2 , ... , x d ) ∈ R d x=(x^1,x^2,\dots,x^d)\in\mathbb{R}^d x=(x1,x2,...,xd)∈Rd 。CNF 有两个核心的研究对象:
- 概率密度路径 (Probability Density Path) p p p : [ 0 , 1 ] × R d → R > 0 [0,1]\times \mathbb{R}^d\rightarrow\mathbb{R}_{>0} [0,1]×Rd→R>0 ,这是一个关于时间的概率密度函数,即有 ∫ p t ( x ) d x = 1 \int p_t(x)dx=1 ∫pt(x)dx=1。
- 关于时间的向量场 (time-dependent vector field) v v v: [ 0 , 1 ] × R d → R d [0,1]\times \mathbb{R}^d\rightarrow\mathbb{R}^d [0,1]×Rd→Rd ,它定义了每一个数据点在状态空间中随时间的变化方向和大小(所以叫向量场),可以理解为描述概率分布随时间变化的速率。
向量场 v t v_t vt 可以用来构建关于时间的微分同胚的映射,称为流 (flow) ϕ \phi ϕ: [ 0 , 1 ] × R d → R d [0,1]\times \mathbb{R}^d\rightarrow\mathbb{R}^d [0,1]×Rd→Rd 。通过常微分方程来定义:
d d t ϕ t ( x ) = v t ( ϕ t ( x ) ) \frac{d}{dt}\phi_t(x)=v_t(\phi_t(x))\\ dtdϕt(x)=vt(ϕt(x))
ϕ 0 ( x ) = x \phi_0(x)=x ϕ0(x)=x
这里的 ϕ t ( x ) \phi_t(x) ϕt(x) 可以理解为 flow ϕ \phi ϕ 在时间 t t t 时的状态,对应于扩散模型中时间步 t t t 的噪声图。 p t ( x ) p_t(x) pt(x) 是概率密度路径 p p p 时的状态,也就是 flow ϕ \phi ϕ 在时间 t t t 的概率分布。
之前,Neural ODE 提出使用一个参数为 θ ∈ R p \theta\in\mathbb{R}^p θ∈Rp 的神经网络 v t ( x ; θ ) v_t(x;\theta) vt(x;θ) 来建模向量场 v t v_t vt ,从而就能够计算出 flow ϕ t \phi_t ϕt,来实现 CNF。
CNF 可以通过 push forward 公式,将一个简单的先验分布 p 0 p_0 p0 (即纯噪声)转化为复杂的分布 p 1 p_1 p1 (即数据分布):
p t = [ ϕ t ] ∗ p 0 p_t=[\phi_t]_*p_0 pt=[ϕt]∗p0
其中 push forward 操作符 ∗ * ∗ 定义为:
ϕ t \] ∗ p 0 ( x ) = p 0 ( ϕ t − 1 ( x ) ) det \[ ∂ ϕ t − 1 ∂ x ( x ) \] \[\\phi_t\]_\*p_0(x)=p_0(\\phi_t\^{-1}(x))\\det\[\\frac{\\partial\\phi_t\^{-1}}{\\partial x}(x)\] \[ϕt\]∗p0(x)=p0(ϕt−1(x))det\[∂x∂ϕt−1(x)
如果满足了上述公式,可以看作是一个向量场 v t v_t vt 生成 了一个概率密度路径 p t p_t pt 。
本文通过连续性方程(Continuity Equation)来测试一个向量场是否能生成一个概率密度路径,这是一个偏微分方程(PDE),给出了概率场生成概率密度路径的充要条件:
d d t p t ( x ) + div ( p t ( x ) v t ( x ) ) = 0 \frac{d}{dt}p_t(x)+\text{div}(p_t(x)v_t(x))=0 dtdpt(x)+div(pt(x)vt(x))=0
其中散度运算符 div \text{div} div 是关于空间变量 x = ( x 1 , ... , x d ) x=(x^1,\dots,x^d) x=(x1,...,xd) 的偏导数: div = ∑ i = 1 d ∂ ∂ x i \text{div}=\sum_{i=1}^d\frac{\partial}{\partial x^i} div=∑i=1d∂xi∂。本文附录 C 还介绍了更多关于 CNF 的前置知识,尤其是如何在空间中任意点 x ∈ R d x\in\mathbb{R}^d x∈Rd 处,计算概率 p 1 ( x ) p_1(x) p1(x)。
为什么说向量场 v t v_t vt "生成" 了概率密度路径 p t p_t pt?为什么要用常微分方程 ODE 来表达?
v t v_t vt 是 ϕ t \phi_t ϕt 的导数(微分)。导数或者说微分,就是一个量随着另一个量极小变化时的变化,其实写成离散形式也好理解了,微分就是变化量: ϕ t ′ = ϕ t + Δ t − ϕ t \phi't=\phi{t+\Delta t}-\phi_t ϕt′=ϕt+Δt−ϕt 。就是从上一个时间点,怎么到下一个时间点,再知道初值 ϕ 0 = x \phi_0=x ϕ0=x 之后,就能从第一个点 "流" 到最后一个点,得到一个路径 p t p_t pt,所以说 "向量场( ϕ t \phi_t ϕt ODE 的解 ϕ t ′ = v t \phi'_t=v_t ϕt′=vt)生成 了一条概率路径"。而 ODE d ϕ t / d t = v ( z t , t ) d\phi_t/dt=v(z_t,t) dϕt/dt=v(zt,t) 定义了一个向量场 v v v 。
三、Flow Matching
在构建生成模型时,我们假设有一个未知的数据分布 q ( x 1 ) q(x_1) q(x1) (注意本文中的符号与扩散模型论文中常用的符号相反,本文中 x 1 x_1 x1 表示真实数据, x 0 x_0 x0 表示随机噪声),我们能从其中采样出大量数据样本,但是不知道该分布的具体函数。
记 p t p_t pt 为概率路径,而 p 0 = p p_0=p p0=p 是一个简单的已知分布(如标准高斯分布 p ( x ) ∼ N ( 0 , I ) p(x)\sim\mathcal{N}(0,\mathbf{I}) p(x)∼N(0,I)),并令 p 1 p_1 p1 在分布上大致与 q q q 相等。Flow Matching 的目标就是去匹配这样一条目标概率路径,从而我们能够从 p 0 p_0 p0 "流动" 到 p 1 p_1 p1,实现生成。如何构造这样一条目标路径,稍后会介绍。
给定一个目标概率密度路径 p t ( x ) p_t(x) pt(x) 以及对应的生成这条路径的向量场 u t ( x ) u_t(x) ut(x),Flow Matching 的目标函数定义为:
L FM ( θ ) = E t , p t ( x ) ∣ ∣ v t ( x ) − u t ( x ) ∣ ∣ 2 \mathcal{L}\text{FM}(\theta)=\mathbb{E}{t,p_t(x)}||v_t(x)-u_t(x)||^2 LFM(θ)=Et,pt(x)∣∣vt(x)−ut(x)∣∣2
其中 θ \theta θ 是 CNF 向量场 v t v_t vt 的参数, t ∼ U ( 0 , 1 ) , x ∼ p t ( x ) t\sim\mathcal{U}(0,1),\ x\sim p_t(x) t∼U(0,1), x∼pt(x) 。简单来说,FM 损失就是通过一个神经网络 v t v_t vt 对向量场 u t u_t ut 进行回归。当损失达到零时,训练好的的 CNF 模型就能够生成各时间 t t t 的 p t ( x ) p_t(x) pt(x),当然就能生成符合数据分布 q ( x 1 ) = p 1 ( x ) q(x_1)=p_1(x) q(x1)=p1(x) 的样本。
Flow Matching 目标函数非常简洁,不过实际中它本身是无法计算的,因为我们并不知道 p t p_t pt 和 u t u_t ut。有许多条概率路径能够实现 p 1 ( x ) ≈ q ( x ) p_1(x)\approx q(x) p1(x)≈q(x),更重要的是,我们无法计算生成目标 p t p_t pt 的 u t u_t ut 的闭式解。
由条件概率路径和条件向量场构建 p t p_t pt 和 u t u_t ut
接下来我们介绍构建目标概率路径 p t p_t pt 和向量场 u t u_t ut 的方法,本方法的思路是通过单个样本构建条件概率路径和条件向量场,再通过积分将条件概率路径/向量场与边缘概率路径/向量场联系起来,从而有一个容易计算的流匹配目标函数。
构建目标概率路径的一个简单方法是通过混合一个更简单的概率路径:给定一个特定的数据样本 x 1 x_1 x1,我们用 p t ( x ∣ x 1 ) p_t(x|x_1) pt(x∣x1) 表示一个条件概率路径,它需要满足:
- 时间 t = 0 t=0 t=0 时 p 0 ( x ∣ x 1 ) = p ( x ) p_0(x|x_1)=p(x) p0(x∣x1)=p(x),也就是说 p 0 ( x ) p_0(x) p0(x) 和样本数据 x 1 x_1 x1 无关,是一个标准噪声分布;
- 在 t = 1 t=1 t=1 时的 p 1 ( x ∣ x 0 ) p_1(x|x_0) p1(x∣x0) 是一个在 x = x 1 x=x_1 x=x1 附近的分布(如一个均值为 x 1 x_1 x1,标准差 σ > 0 \sigma>0 σ>0 足够小的正态分布 p 1 ( x ∣ x 1 ) = N ( x ∣ x 1 , σ 2 I ) p_1(x|x_1)=\mathcal{N}(x|x_1,\sigma^2\mathbf{I}) p1(x∣x1)=N(x∣x1,σ2I))。也就是说 t = 1 t=1 t=1 时要大致符合数据分布,即 p 1 ( x ) ≈ q ( x ) p_1(x)\approx q(x) p1(x)≈q(x) 。
将条件概率路径 p t ( x ∣ x 1 ) p_t(x|x_1) pt(x∣x1) 对所有的 q ( x 1 ) q(x_1) q(x1) 进行积分(相当于遍历数据集中所有的真实数据),就得到了我们想要的边缘概率路径 p t ( x ) p_t(x) pt(x):
p t ( x ) = ∫ p t ( x ∣ x 1 ) q ( x 1 ) d x 1 p_t(x)=\int p_t(x|x_1)q(x_1)d{x_1} pt(x)=∫pt(x∣x1)q(x1)dx1
特别地,当时间 t = 1 t=1 t=1 时,边缘概率 p 1 p_1 p1 是一个混合分布,能够对数据分布 q q q 进行很好的近似:
p 1 ( x ) = ∫ p 1 ( x ∣ x 1 ) q ( x 1 ) d x 1 ≈ q ( x ) p_1(x)=\int p_1(x|x_1)q(x_1)dx_1\approx q(x) p1(x)=∫p1(x∣x1)q(x1)dx1≈q(x)
我们也可以通过对条件向量场进行 "边缘化",来定义一个边缘向量场 (marginal vector field) (假设对所有的 t , x t,x t,x , p t ( x ) > 0 p_t(x)>0 pt(x)>0):
u t ( x ) = ∫ u t ( x ∣ x 1 ) p t ( x ∣ x 1 ) q ( x 1 ) p t ( x ) d x 1 u_t(x)=\int u_t(x|x_1)\frac{p_t(x|x_1)q(x_1)}{p_t(x)}dx_1 ut(x)=∫ut(x∣x1)pt(x)pt(x∣x1)q(x1)dx1
其中 u t ( ⋅ ∣ x 1 ) : R d → R d u_t(\cdot|x_1):\ \mathbb{R}^d\rightarrow\mathbb{R}^d ut(⋅∣x1): Rd→Rd 是生成 p t ( ⋅ ∣ x 1 ) p_t(\cdot|x_1) pt(⋅∣x1) 的条件向量场。
那么,这种对条件向量场积分,来构造的边缘向量场 u t ( x ) u_t(x) ut(x),能否生成对应的边缘概率路径 p t ( x ) p_t(x) pt(x) 呢?作者证明,是可以的。原文中附录 A 给出了完整的证明过程,其实要证明就是上述构造边缘概率路径/向量场的形式,能够满足连续性方程。
这样就将条件向量场(可以生成条件概率路径)和边缘向量场(可以生成边缘概率路径)联系了起来。从而我们就可以将未知且难以计算的边缘概率场转换为更简单的条件概率场。条件概率场定义起来要简单得多,因为它仅依赖于单个数据样本。正式地表述为:
定理1 给定条件概率路径 p ( x ∣ x 1 ) p(x|x_1) p(x∣x1) 以生成该路径的条件向量场 u ( x ∣ x 1 ) u(x|x_1) u(x∣x1),对于任意数据分布 q ( x 1 ) q(x_1) q(x1),边缘向量场 u t u_t ut 和 p t p_t pt 满足连续性方程,即 u t u_t ut 能够生成 p t p_t pt
条件流匹配 Conditional Flow Matching
遗憾的是,由于边缘向量场和边缘概率路径中的积分无法计算,我们还是无法得到 u t u_t ut ,从而也就无法直接计算原始 Flow Matching 目标函数。这里,作者提出了一个更简单的目标函数,它能导出与原目标函数相同的最优解。具体来说,作者提出了 条件流匹配 (Conditional Flow Matching) 目标:
L CFM ( θ ) = E t , q ( x 1 ) , p t ( x ∣ x 1 ) ∣ ∣ v t ( x ) − u t ( x ∣ x 1 ) ∣ ∣ 2 \mathcal{L}\text{CFM}(\theta)=\mathbb{E}{t,q(x_1),p_t(x|x_1)}||v_t(x)-u_t(x|x_1)||^2 LCFM(θ)=Et,q(x1),pt(x∣x1)∣∣vt(x)−ut(x∣x1)∣∣2
其中 t ∼ U ( 0 , 1 ) , x 1 ∼ q ( x 1 ) t\sim\mathcal{U}(0,1),\ x_1\sim q(x_1) t∼U(0,1), x1∼q(x1),而此时 x ∼ p t ( x ∣ x 1 ) x\sim p_t(x|x_1) x∼pt(x∣x1)。也就是说,我们不回归向量场 u t ( x ) u_t(x) ut(x) 了,而是改为回归条件向量场 u t ( x ∣ x 1 ) u_t(x|x_1) ut(x∣x1)。不同于 FM 目标函数,在 CFM 目标函数中,只要我们能从 p t ( x ∣ x 1 ) p_t(x|x_1) pt(x∣x1) 中采样,并计算 u t ( x ∣ x 1 ) u_t(x|x_1) ut(x∣x1),就可以计算出无偏估计。而由于我们是在单个样本上进行的定义,这两点要求都很容易满足。
作者证明了:
定理2 假设对所有的 x ∈ R d x\in\mathbb{R}^d x∈Rd 和 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1],都有 p t ( x ) > 0 p_t(x)>0 pt(x)>0,那么 L CFM \mathcal{L}\text{CFM} LCFM 和 L FM \mathcal{L}\text{FM} LFM 是相等的(至多差一个与 θ \theta θ 无关的常数),即 ∇ θ L CFM ( θ ) = ∇ θ L FM ( θ ) \nabla_\theta\mathcal{L}\text{CFM}(\theta)=\nabla\theta\mathcal{L}_\text{FM}(\theta) ∇θLCFM(θ)=∇θLFM(θ) 。
也就是说,优化 CFM 目标(在期望上)等同于优化 FM 目标。因此,我们可以用 CFM 目标训练一个 CNF 来生成边际概率路径 p t p_t pt,在 t = 1 t=1 t=1 时近似未知数据分布 q q q,而无需已知边缘概率路径或边缘向量场。我们只需要设计合适的条件概率路径和条件向量场。
四、高斯条件概率路径和条件向量场
CFM 目标适用于所有的条件概率路径和条件向量场。本节中,我们重点讨论高斯条件概率路径族的 p t ( x ∣ x 1 ) p_t(x|x_1) pt(x∣x1) 和 u t ( x ∣ x 1 ) u_t(x|x_1) ut(x∣x1)。即,我们考虑如下形式的高斯条件概率路径:
p t ( x ∣ x 1 ) = N ( x ∣ μ t ( x 1 ) , σ t 2 ( x 1 ) I ) p_t(x|x_1)=\mathcal{N}(x|\mu_t(x_1),\sigma_t^2(x_1)\mathbf{I}) pt(x∣x1)=N(x∣μt(x1),σt2(x1)I)
其中 μ : [ 0 , 1 ] × R d → R d \mu:[0,1]\times \mathbb{R}^d\rightarrow\mathbb{R}^d μ:[0,1]×Rd→Rd 和 σ : [ 0 , 1 ] × R → R > 0 \sigma:[0,1]\times\mathbb{R}\rightarrow\mathbb{R}_{>0} σ:[0,1]×R→R>0 分别是关于时间 t t t 的高斯分布的均值和标准差。需要满足:
- 在时间 t = 0 t=0 t=0 时,满足 μ 0 ( x 1 ) = 0 , σ 0 ( x 1 ) = 1 \mu_0(x_1)=0,\sigma_0(x_1)=1 μ0(x1)=0,σ0(x1)=1,从而所有的条件概率路径都收敛到标准高斯分布 p ( x ) = N ( x ∣ 0 , I ) p(x)=\mathcal{N}(x|0,\mathbf{I}) p(x)=N(x∣0,I);
- 在时间 t = 1 t=1 t=1 时,满足 KaTeX parse error: Got function '\min' with no arguments as subscript at position 37: ...1(x_1)=\sigma\̲m̲i̲n̲,其中 KaTeX parse error: Got function '\min' with no arguments as subscript at position 8: \sigma_\̲m̲i̲n̲ 需足够小,使得 p 1 ( x ∣ x 1 ) p_1(x|x_1) p1(x∣x1) 是足够聚集于中心 x 1 x_1 x1 的高斯分布。
存在无限多个向量场可以生成任何特定的概率路径,但这些中的绝大多数是由于存在使底层分布不变的分量(比如像连续性方程中添加一个无散度的分量),导致的不必要的额外计算。作者使用最简单的,对应于高斯分布的标准变换的向量场。具体来说,考虑条件于 x 1 x_1 x1 的流:
ψ t ( x ) = σ t ( x 1 ) x + μ t ( x 1 ) \psi_t(x)=\sigma_t(x_1)x+\mu_t(x_1) ψt(x)=σt(x1)x+μt(x1)
当 x x x 是标准的高斯分布时, ψ t ( x ) \psi_t(x) ψt(x) 是一个仿射变换,映射到均值为 μ t ( x 1 ) \mu_t(x_1) μt(x1)、标准差为 σ t ( x 1 ) \sigma_t(x_1) σt(x1) 的正态分布随机变量。也就是说,根据上式, ψ t \psi_t ψt 的前向过程从噪声分布 p 0 ( x ∣ x 1 ) p_0(x|x_1) p0(x∣x1) 流向 p t ( x ∣ x 1 ) p_t(x|x_1) pt(x∣x1) ,即:
ψ t \] ∗ p ( x ) = p t ( x ∣ x 1 ) \[\\psi_t\]_\*p(x)=p_t(x\|x_1) \[ψt\]∗p(x)=pt(x∣x1) 生成这个条件概率路径 p t ( x ∣ x 1 ) p_t(x\|x_1) pt(x∣x1) 的条件向量场 u t ( x ∣ x 1 ) u_t(x\|x_1) ut(x∣x1) 为: d d t ψ t ( x ) = u t ( ψ t ( x ) ∣ x 1 ) \\frac{d}{dt}\\psi_t(x)=u_t(\\psi_t(x)\|x_1) dtdψt(x)=ut(ψt(x)∣x1) 将 ψ t \\psi_t ψt 重写为仅关于 x 0 x_0 x0,并将上式代入到 CFM 损失中,有: L CFM ( θ ) = E t , q ( x 1 ) , p ( x 0 ) ∣ ∣ v t ( ψ t ( x 0 ) ) − d d t ψ t ( x 0 ) ∣ ∣ 2 \\mathcal{L}_\\text{CFM}(\\theta)=\\mathbb{E}_{t,q(x_1),p(x_0)}\|\|v_t(\\psi_t(x_0))-\\frac{d}{dt}\\psi_t(x_0)\|\|\^2 LCFM(θ)=Et,q(x1),p(x0)∣∣vt(ψt(x0))−dtdψt(x0)∣∣2 由于 ψ t \\psi_t ψt 是可逆的仿射映射,我们可以闭式计算出 u t u_t ut。 记 f ′ f' f′ 表示关于时间的函数 f f f 对时间的微分,即 f ′ = d d t f f'=\\frac{d}{dt}f f′=dtdf。 **定理3 设 p t ( x ∣ x 1 ) p_t(x\|x_1) pt(x∣x1) 是一个高斯概率路径, ψ t \\psi_t ψt 是其对应的 flow map,那么有唯一的向量场 ψ t \\psi_t ψt,其形式为:** u t ( x ∣ x 1 ) = σ t ′ ( x 1 ) σ t ( x 1 ) ( x − μ t ( x 1 ) ) + μ t ′ ( x 1 ) u_t(x\|x_1)=\\frac{\\sigma'_t(x_1)}{\\sigma_t(x_1)}(x-\\mu_t(x_1))+\\mu'_t(x_1) ut(x∣x1)=σt(x1)σt′(x1)(x−μt(x1))+μt′(x1) **该向量场 u t ( x ∣ x 1 ) u_t(x\|x_1) ut(x∣x1) 可以生成高斯路径 p t ( x ∣ x 1 ) p_t(x\|x_1) pt(x∣x1)。** #### 高斯条件概率路径的特殊情形 我们的形式化对于任意函数 μ t ( x 1 ) \\mu_t(x_1) μt(x1) 和 σ t ( x 1 ) \\sigma_t(x_1) σt(x1) 都是完全通用的,我们可以将它们设置为任何满足所需边界条件的可微函数。本节讨论两个实例,首先讨论已有的经典扩散模型(如 VP/VE)在本文形式化下的推导。然后,由于我们直接使用概率路径工作,可以完全不依赖于关于扩散过程的推理。因此,我们可以直接基于 Wasserstein-2 最优传输解来制定一个概率路径,这是第二个实例。 ##### 例子1:Diffusion Conditional VFs 扩散模型对一个真实数据样本逐渐添加噪声,直到其成为纯噪声。扩散模型可以表示为随机过程,其具有一定的要求,从而对任意时间 t t t 有闭式表示。选择不同的均值 μ t ( x 1 ) \\mu_t(x_1) μt(x1) 和标准差 σ t ( x 1 ) \\sigma_t(x_1) σt(x1),就得到特定高斯条件概率路径 p t ( x ∣ x 1 ) p_t(x\|x_1) pt(x∣x1) 。 首先来看 Variance Exploding,其反向(噪声-\>数据)路径为: p t ( x ) = N ( x ∣ x 1 , σ 1 − t 2 I ) p_t(x)=\\mathcal{N}(x\|x_1,\\sigma\^2_{1-t}\\mathbf{I}) pt(x)=N(x∣x1,σ1−t2I) 其中 σ t \\sigma_t σt 是一个单增函数, σ 0 = 0 , σ 1 \> \> 1 \\sigma_0=0,\\sigma_1\>\>1 σ0=0,σ1\>\>1。上式这种 VE 扩散模型,是选择了均值和标准差分别为 μ t ( x 1 ) = x 1 , σ t ( x 1 ) = σ 1 − t \\mu_t(x_1)=x_1,\\sigma_t(x_1)=\\sigma_{1-t} μt(x1)=x1,σt(x1)=σ1−t 。带入到定理 3 的公式中: u t ( x ∣ x 1 ) = − σ 1 − t ′ σ 1 − t ( x − x 1 ) u_t(x\|x_1)=-\\frac{\\sigma'_{1-t}}{\\sigma_{1-t}}(x-x_1) ut(x∣x1)=−σ1−tσ1−t′(x−x1) 另一种经典的扩散模型 Variance Preserving 扩散路径的形式为: p t ( x ∣ x 1 ) = N ( x ∣ α 1 − t x 1 , ( 1 − α 1 − t 2 ) I ) α t = e − 1 2 T ( t ) T ( t ) = ∫ 0 t β ( s ) d s p_t(x\|x_1)=\\mathcal{N}(x\|\\alpha_{1-t}x_1,(1-\\alpha\^2_{1-t})\\mathbf{I})\\\\ \\alpha_t=e\^{-\\frac{1}{2}T(t)}\\\\ T(t)=\\int_0\^t\\beta(s)ds pt(x∣x1)=N(x∣α1−tx1,(1−α1−t2)I)αt=e−21T(t)T(t)=∫0tβ(s)ds 其中 β \\beta β 是关于 t t t 的 noise scale 函数。上式是选择了均值和标准差分别为 μ t ( x 1 ) = α 1 − t x 1 , σ t ( x 1 ) = 1 − α 1 − t 2 \\mu_t(x_1)=\\alpha_{1-t}x_1,\\sigma_t(x_1)=\\sqrt{1-\\alpha_{1-t}\^2} μt(x1)=α1−tx1,σt(x1)=1−α1−t2 。带入到定理 3 的公式中: u t ( x ∣ x 1 ) = α 1 − t ′ 1 − α 1 − t 2 ( α 1 − t x − x 1 ) = − T ′ ( 1 − t ) 2 \[ e − T ( 1 − t ) x − e − 1 2 T ( 1 − t ) x 1 1 − e − T ( 1 − t ) \] u_t(x\|x_1)=\\frac{\\alpha'_{1-t}}{1-\\alpha\^2_{1-t}}(\\alpha_{1-t}x-x_1)=-\\frac{T'(1-t)}{2}\[\\frac{e\^{-T(1-t)}x-e\^{-\\frac{1}{2}T(1-t)}x_1}{1-e\^{-T(1-t)}}\] ut(x∣x1)=1−α1−t2α1−t′(α1−tx−x1)=−2T′(1−t)\[1−e−T(1−t)e−T(1−t)x−e−21T(1−t)x1
实际上,本文在指定特定的条件扩散过程时构建出的条件向量场 u t ( x ∣ x 1 ) u_t(x|x_1) ut(x∣x1) ,与宋飏等人(Diff SDE 论文,公式 12)中给出的确定性概率流模型是相符的。并且,将扩散条件向量场与 FM 训练目标结合起来,能得到另一种训练 score matching 的方法,作者发现该方法训练起来更加稳定。
作者还指出,上述提到的这些概率路径通过扩散过程推导得出,所以他们在最终的时间步并没有达到真正的噪声分布(Zero Terminal SNR 也提出了一样的问题)。实际中, p 0 ( x ) p_0(x) p0(x) 只是通过一个合适的高斯分布近似,来进行采样和似然计算。而本文提出的构造方式,则可以对概率路径有完全的控制,可以直接设置 μ t \mu_t μt 和 σ t \sigma_t σt。接下来,我们就试试这样做。
例子2:Optimal Transport Conditional VFs
一个更自然的选择是将均值和标准差定义为简单的线性变换,即:
KaTeX parse error: Got function '\min' with no arguments as subscript at position 42: ...x)=1-(1-\sigma_\̲m̲i̲n̲)t
根据定理 3,产生上述路径的向量场为:
KaTeX parse error: Got function '\min' with no arguments as subscript at position 33: ...{x_1-(1-\sigma_\̲m̲i̲n̲)x}{1-(1-\sigma...
其中 t ∈ [ 0 , 1 ] t\in[0,1] t∈[0,1]。其对应的 flow 为:
KaTeX parse error: Got function '\min' with no arguments as subscript at position 25: ...)=(1-(1-\sigma_\̲m̲i̲n̲)t)x+tx_1
此时,CFM 损失为:
KaTeX parse error: Got function '\min' with no arguments as subscript at position 95: ...(x_1-(1-\sigma_\̲m̲i̲n̲)x_0)||^2
本文这种线性的均值标准差构造方法,不仅能得到简单直观的路径,实际上在以下意义上也是最优的。条件流 ψ t ( x ) \psi_t(x) ψt(x) 实际上是两个高斯分布 p 0 ( x ∣ x 1 ) p_0(x|x_1) p0(x∣x1) 和 p 1 ( x ∣ x 1 ) p_1(x|x_1) p1(x∣x1) 之间的最优传输映射(Optimal Transport (OT) Displacement Map)。最优传输插值(OT Interpolant),即是一个概率路径,被定义为:
p t = [ ( 1 − t ) id + t ψ ] ∗ p 0 p_t=[(1-t)\text{id}+t\psi]_*p_0 pt=[(1−t)id+tψ]∗p0
其中 ψ : R d → R d \psi:\mathbb{R}^d\rightarrow\mathbb{R}^d ψ:Rd→Rd 是从 p 0 p_0 p0 到 p 1 p_1 p1 的最优传输映射, id \text{id} id 表示恒等映射,即 id ( x ) = x \text{id}(x)=x id(x)=x。 ( 1 − t ) id + t ψ (1-t)\text{id}+t\psi (1−t)id+tψ 即 OT displacement map。之前的研究表明,在这种情况汇总,两个高斯分布(其中第一个是标准高斯)的 OT displacement map 形如式 23。
直观地说,在最优传输位移图下,粒子总是沿着直线轨迹并以恒定速度移动。下图展示了扩散和最优传输条件向量场的采样路径。作者还发现,从扩散路径中采样的轨迹可能会"超出"最终样本,导致不必要的回溯,而最优传输路径则保证保持直线。
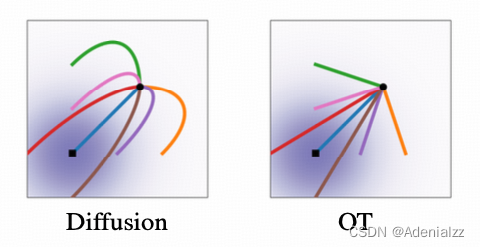
下图比较了扩散条件得分函数(典型扩散方法中的回归目标),即 ∇ log p t ( x ∣ x 1 ) \nabla \log p_t(x|x_1) ∇logpt(x∣x1),与 OT 条件向量场。两个示例中的起始 p_0 和结束 p 1 p_1 p1高斯分布是相同的。一个有趣的观察是,最优传输向量场在时间上具有恒定的方向,这无疑会导致一个更简单的回归任务。这个属性也可以从 OT 的形式中验看出,因为向量场可以写成 u t ( x ∣ x 1 ) = g ( t ) h ( x ∣ x 1 ) u_t(x|x_1) = g(t)h(x|x_1) ut(x∣x1)=g(t)h(x∣x1) 的形式。最后,我们注意到,尽管条件流是最优的,但这并不意味着边际向量场是最优传输解。尽管如此,我们期望边际向量场保持相对简单。
