前言:
线段树:用树来表示一个一个的线段区间。
1、为什么要使用线段树?
题目:给定一个数组nums,我们有两种下面两种操作
1、查询nums数组下标i到下标j的和;
2、将nums数组指定下标的值改为指定的一个新值;
如果上面两种操作频繁交叉进行,如何使整体效率更高。
方案一:更新操作O1
每次查询操作都从i加到j,每次更新直接更新对应下标。
缺点:如果每次查询操作都是查整个数组的和,一下子来了几万个查询操作,则每次都是O(n),几万次O(n),比较浪费时间。
方案二:查询操作O1
新建一个同等大小数组dp,dp【i】用于记录从nums[0]加到nums[i]的值。
缺点:虽然查询操作从O(n),变成O1(dp[j]-dp[i-1])。但是更新操作需要变成了O(n),每次更新都需要维护dp数组,从更新处开始往后面的值都需要重新计算,如果一次性来了大量的更新操作请求,则比较浪费时间。
方案三:线段树(查询Ologn,更新Ologn)
2、线段树为什么开4n空间?
1、假设n刚好是2的整数次阶乘,则n的满二叉树具有下面特征:
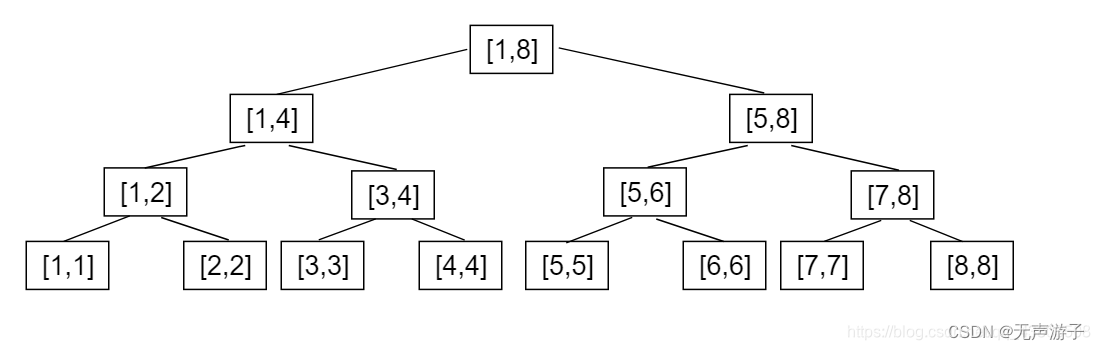
1)树的层高:h=log2^n+1;
2)树的最后一层的节点数:an=2^(h-1);
3)树的节点数总和:sn=2n-1;
那为什么要开4n空间呢?因为如果n=9,呢?即n不是刚好2的某个整数的阶乘,这时候会在满二叉树的基础上多出一层来。
多出来一层的节点数为:an+1=2^h;
那么树的节点数总和就变成了:sn=2n-1+2^h,h=log2^n+1,所以:sn=4n-1。
因为存储的时候下标从1开始,所以我们给4n的空间。
3、构造线段树
1、节点数组下标分配:从上到下,从左到右
2、父子节点间下标关系:
l = fa*2 (左子树下标为父节点下标的两倍)
r = fa*2+1(右子树下标为父节点下标的两倍+1)
3、代码如下:
java
class Tree{
int[] nums;
int[] tree;
public Tree(int[] nums){
this.nums = nums;
int n = nums.length;
tree = new int[4*n];
build(nums,0,0,0);
}
// l = fa*2 (左子树下标为父节点下标的两倍)
// r = fa*2+1(右子树下标为父节点下标的两倍+1)
public void build(int[] nums,int id,int l,int r){
if(l==r){
tree[id] = nums[l];
return;
}
int mid = (l + r)/2;
build(nums,2*id,l,mid);
build(nums,2*id+1,mid,r);
tree[id] = tree[2*id]+tree[2*id+1];
}
}4、线段树区间查询
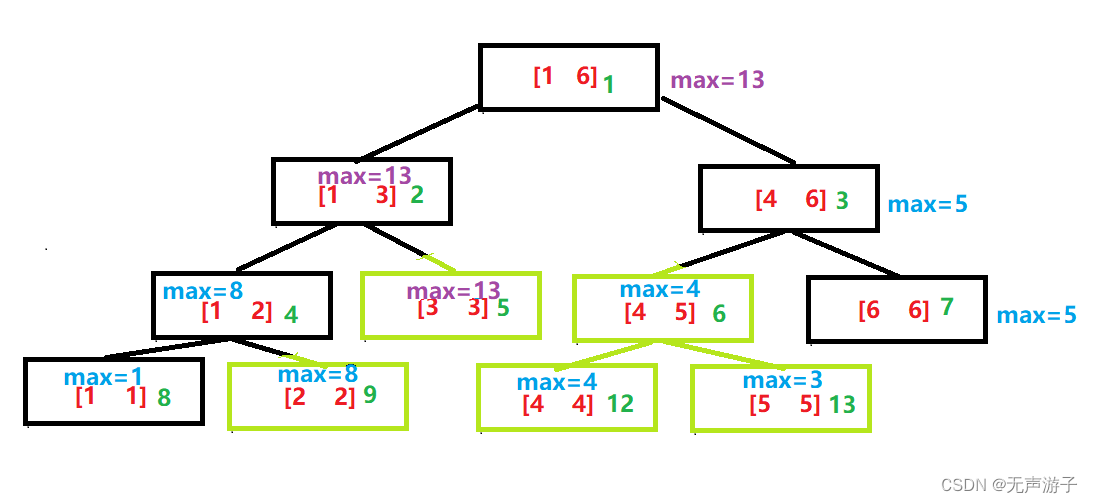
我们知道线段树的每个结点存储的都是一段区间的信息 ,如果我们刚好要查询这个区间,那么则直接返回这个结点的信息即可,比如对于上面线段树,如果我直接查询[1,6]这个区间的最值,那么直接返回根节点信息返回13即可,但是一般我们不会凑巧刚好查询那些区间,比如现在我要查询[2,5]区间的最值,这时候该怎么办呢,我们来看看哪些区间被[2,5]包含了。
一共有5个区间,而且我们可以发现[4,5]这个区间已经包含了两个子树的信息([4,4],[5,5]),所以我们需要查询的区间只有三个,分别是[2,2],[3,3],[4,5],我们从根节点开始往下递归,如果当前结点是被要查询的区间包含了的,则返回这个结点的信息,这样从根节点往下递归,时间复杂度也是O(logN)。
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
原文链接:https://blog.csdn.net/weq2011/article/details/128791426
java
// 查询指定区间内的值的和
public int find(int id,int l,int r,int x,int y){
// 当区间完全在要求查找区间范围内时,就是我们要的值
if(l>=x && r<=y){
return tree[id];
}
int mid = (l + r)/2;
int sum = 0;
// 如果值存在于左子树,则需要进行查找
if(x<=mid){
sum+=find(2*id,l,mid,x,y);
}
// 如果值存在于右子树,则需要进行查找
if(y>mid){
sum+=find(2*id+1,mid+1,r,x,y);
}
return sum;
}5、线段树更新
id:从线段树哪个下标开始检索
l:数值区间左
r:数值区间右
index:需要更新的dp下标
val:更新的值
java
// 更新指定下标的值
// 指定下标
public void update(int id,int l,int r,int index,int val){
tree[id] = tree[id]+val;
if(l == index && r == index){
return;
}
int mid = (l + r)/2;
if(index<=mid){
update(2*id,l,mid,index,val);
}
if(index>mid){
update(2*id+1,mid+1,r,index,val);
}
}6、完整案例及代码
3187. 数组中的峰值
数组 arr 中 大于 前面和后面相邻元素的元素被称为 峰值 元素。
给你一个整数数组 nums 和一个二维整数数组 queries 。
你需要处理以下两种类型的操作:
queries[i] = [1, li, ri],求出子数组nums[li..ri]中 峰值 元素的数目。queries[i] = [2, indexi, vali],将nums[indexi]变为vali。
请你返回一个数组 answer ,它依次包含每一个第一种操作的答案。
注意:
- 子数组中 第一个 和 最后一个 元素都 不是 峰值元素。
示例 1:
**输入:**nums = [3,1,4,2,5], queries = [[2,3,4],[1,0,4]]
输出:[0]
解释:
第一个操作:我们将 nums[3] 变为 4 ,nums 变为 [3,1,4,4,5] 。
第二个操作:[3,1,4,4,5] 中峰值元素的数目为 0 。
示例 2:
**输入:**nums = [4,1,4,2,1,5], queries = [[2,2,4],[1,0,2],[1,0,4]]
输出:[0,1]
解释:
第一个操作:nums[2] 变为 4 ,它已经是 4 了,所以保持不变。
第二个操作:[4,1,4] 中峰值元素的数目为 0 。
第三个操作:第二个 4 是 [4,1,4,2,1] 中的峰值元素。
提示:
3 <= nums.length <= 1051 <= nums[i] <= 1051 <= queries.length <= 105queries[i][0] == 1或者queries[i][0] == 2- 对于所有的
i,都有:queries[i][0] == 1:0 <= queries[i][1] <= queries[i][2] <= nums.length - 1queries[i][0] == 2:0 <= queries[i][1] <= nums.length - 1,1 <= queries[i][2] <= 105
1)线段树求解代码:
java
package algorithm.temp;
import java.util.ArrayList;
import java.util.List;
class Test2 {
static final int COUNT_PEAK = 1, UPDATE = 2;
public static void main(String[] args) {
int[][] queyy = new int[4][3];
queyy[0][0] = 2;
queyy[0][1] = 0;
queyy[0][2] = 2;
queyy[1][0] = 1;
queyy[1][1] = 0;
queyy[1][2] = 3;
// queyy[0][0] = 1;
// queyy[0][1] = 2;
// queyy[0][2] = 4;
// queyy[1][0] = 1;
// queyy[1][1] = 0;
// queyy[1][2] = 1;
queyy[2][0] = 1;
queyy[2][1] = 3;
queyy[2][2] = 3;
queyy[3][0] = 2;
queyy[3][1] = 3;
queyy[3][2] = 5;
System.out.println(countOfPeaks(new int[] {9,7,5,8,9}, queyy));
;
}
public static List<Integer> countOfPeaks(int[] nums, int[][] queries) {
List<Integer> li = new ArrayList<Integer>();
int[] dp = new int[nums.length];
dp[0] = 0;
for(int i=1;i<nums.length;i++){
if(isTopElement(nums,i)){
dp[i]= 1;
dp[++i] = 0;
};
}
Tree tree = new Tree(dp);
for(int i=0;i<queries.length;i++){
int[] temp = queries[i];
if(temp[0] == 1){
int x = temp[1];
int y = temp[2];
li.add(y-x>1?tree.find(1, 0, dp.length-1, x+1, y-1):0);
}else{
int index = temp[1];
int val = temp[2];
nums[index] = val;
for(int k=-1;k<=1;k++){
int num=0;
if(index+k>0 && index+k<nums.length-1){
num=isTopElement(nums,index+k)?1-dp[index+k]:0-dp[index+k];
tree.update(1,0, dp.length-1, index+k, num);
dp[index+k] = dp[index+k]+num;
}
}
}
}
return li;
}
public static boolean isTopElement(int[] nums,int index) {
if(index-1>=0 && index+1<=nums.length-1 && nums[index]>nums[index-1] && nums[index]>nums[index+1]){
return true;
}
return false;
}
}
class Tree{
int[] nums;
int[] tree;
public Tree(int[] nums){
this.nums = nums;
int n = nums.length;
tree = new int[4*n];
build(nums,1,0,n-1);
}
// l = fa*2 (左子树下标为父节点下标的两倍)
// r = fa*2+1(右子树下标为父节点下标的两倍+1)
public void build(int[] nums,int id,int l,int r){
if(l==r){
tree[id] = nums[l];
return;
}
int mid = (l + r)/2;
build(nums,2*id,l,mid);
build(nums,2*id+1,mid+1,r);
tree[id] = tree[2*id]+tree[2*id+1];
}
// 查询指定区间内的值的和
public int find(int id,int l,int r,int x,int y){
// 当区间完全在要求查找区间范围内时,就是我们要的值
if(l>=x && r<=y){
return tree[id];
}
int mid = (l + r)/2;
int sum = 0;
// 如果值存在于左子树,则需要进行查找
if(x<=mid){
sum+=find(2*id,l,mid,x,y);
}
// 如果值存在于右子树,则需要进行查找
if(y>mid){
sum+=find(2*id+1,mid+1,r,x,y);
}
return sum;
}
// 更新指定下标的值
// 指定下标
public void update(int id,int l,int r,int index,int val){
tree[id] = tree[id]+val;
if(l == index && r == index){
return;
}
int mid = (l + r)/2;
if(index<=mid){
update(2*id,l,mid,index,val);
}
if(index>mid){
update(2*id+1,mid+1,r,index,val);
}
}
}2)暴力求解代码
(执行效率低下,本人第一次就是写的这段代码,案例跑超时):
java
class Solution {
public List<Integer> countOfPeaks(int[] nums, int[][] queries) {
List<Integer> li = new ArrayList<Integer>();
int[] dp = new int[nums.length];
dp[0] = 0;
for(int i=1;i<nums.length;i++){
if(isTopElement(nums,i)){
dp[i]= 1;
dp[++i] = 0;
};
}
for(int i=0;i<queries.length;i++){
int[] temp = queries[i];
if(temp[0] == 1){
int sum = 0;
for(int k=temp[1]+1;k<temp[2]&&k<nums.length;k++){
sum+=dp[k];
}
li.add(sum);
}else{
nums[temp[1]] = temp[2];
for(int k=temp[1]-1;k<=temp[1]+1;k++){
if(isTopElement(nums,k)){
dp[k] = 1;
}else if(k>0&&k<nums.length){
dp[k] = 0;
}
}
}
}
return li;
}
public boolean isTopElement(int[] nums,int index) {
if(index-1>=0 && index+1<=nums.length-1 && nums[index]>nums[index-1] && nums[index]>nums[index+1]){
return true;
}
return false;
}
}