一、实验原理
根据幂法,Euler法的相关知识和算法编程完成本实验
二、实验内容
见第7 章PPT :用规范化幂法计算下面矩阵的按模最大特征值及对应的特征向量
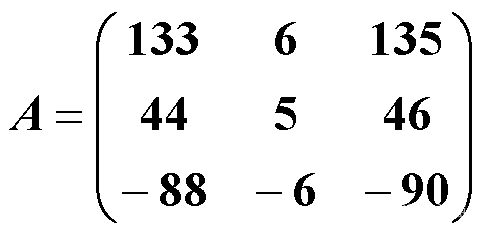
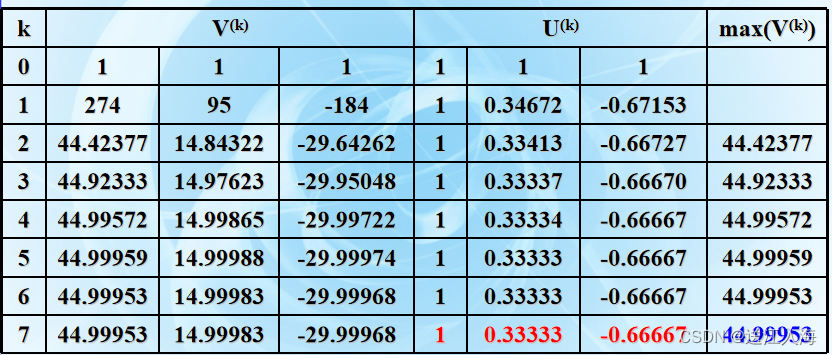
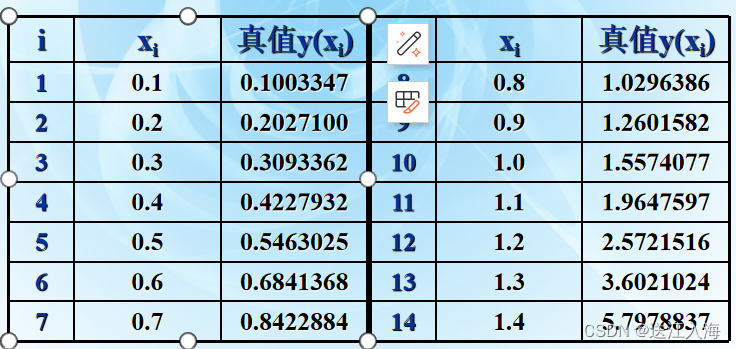
见第8 章PPT :分别用简单欧拉法和改进欧拉法对如下初值问题作验证性计算
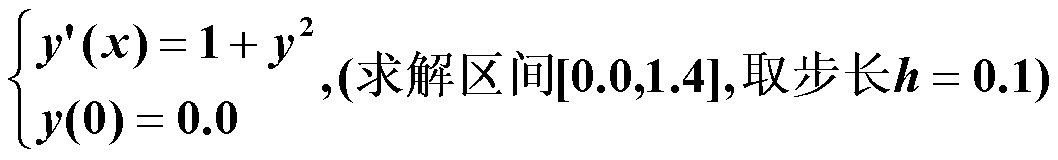
三、实验过程 (可以文字说明 + 运行结果截图)
1 )规范化幂法
实验说明:
数据说明
1.矩阵A:
一个 3×3 的系数矩阵,表示为 array[N][N]。
2.初始向量
一个长度为 3 的初始猜测向量,表示为 a0[N]。
3.迭代次数:
count:迭代次数。
收敛条件:
ϵ=0.000001:绝对误差阈值,当特征值的相对变化小于该值时停止迭代。
代码说明
1.GetMax函数:
获取数组中的最大值。
- matrixMulti函数:
对矩阵 A 和初始向量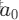
进行矩阵相乘,得到迭代后的向量。
- main函数:
定义矩阵 A 和初始向量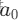
在迭代过程中,对初始向量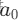
进行规范化,然后进行矩阵相乘,得到迭代后的向量。
计算特征值的相对变化,若小于收敛条件 ϵ,则停止迭代。
输出迭代次数和最大特征值。
算法说明
幂法:用于估计矩阵的最大特征值和对应的特征向量。
在每次迭代中,先对当前向量进行规范化,然后进行矩阵与向量的乘积。
通过计算每次迭代后向量中的最大元素,来估计最大特征值的大小。
当最大特征值的相对变化小于给定的绝对误差阈值时,停止迭代。
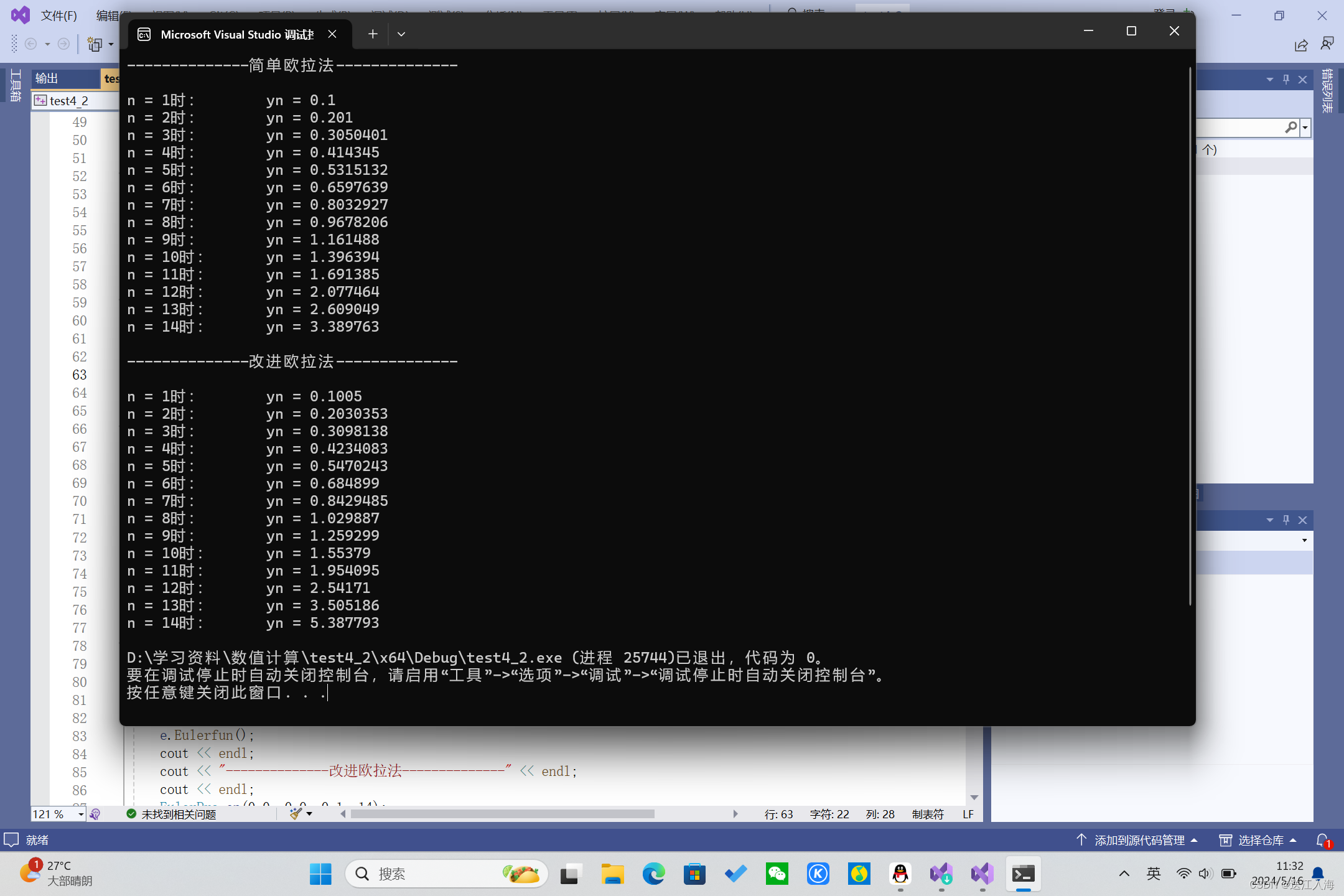
运行截图:
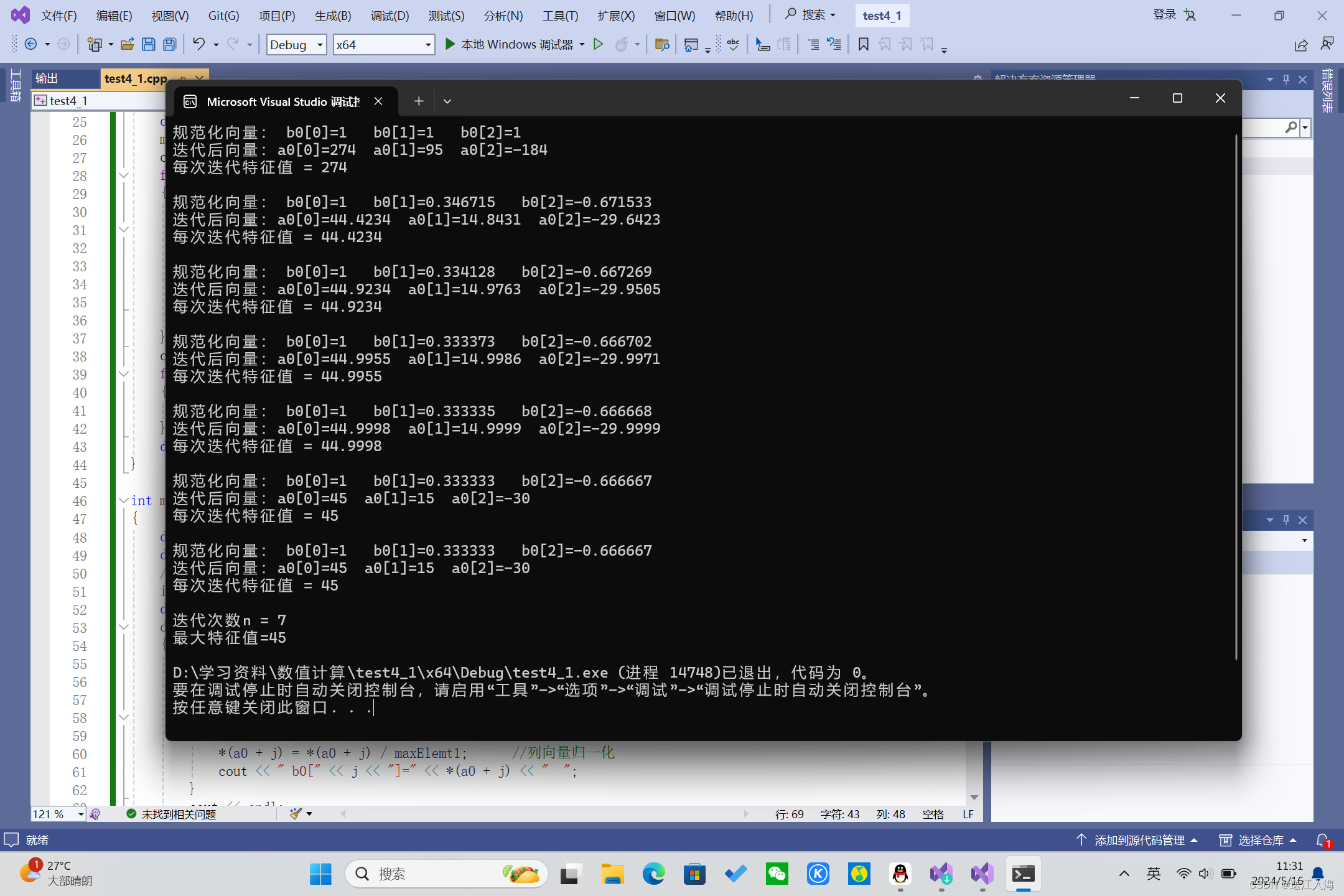
2 )简单欧拉法和改进欧拉法
实验说明:
数据说明
1.初始点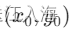
2.步长 h
3.迭代次数 n。
代码说明
- Euler类:
实现了简单欧拉法。
包括成员函数 fun 用于定义微分方程。
成员函数 Eulerfun 执行简单欧拉法迭代计算。
2.EulerPro类继承自 Euler:
实现了改进的欧拉法。
在 EulerProfun 函数中使用了改进的公式进行迭代计算。
- main函数:
创建了简单欧拉法和改进欧拉法的对象,并调用相应的函数进行计算。
打印了计算结果。
算法说明
1.简单欧拉法:
使用简单欧拉法逐步逼近微分方程的数值解。
在每一步中,通过计算当前点的斜率,然后使用步长 h进行线性近似,从而得到下一个点的近似值。
2.改进欧拉法:
改进欧拉法在简单欧拉法的基础上,通过使用改进的公式来提高精度。
在每一步中,不仅仅使用当前点的斜率,还使用了下一个点的斜率,然后取两者平均值作为斜率,从而得到下一个点的近似值。
运行截图: