最长上升子序列模型——AcWing 272. 最长公共上升子序列

最长上升子序列模型

定义

给定一个序列，如整数序列或字符序列，最长上升子序列是指其中最长的子序列，满足子序列中的元素依次递增。最长上升子序列模型是一种在给定序列中寻找最长上升子序列的问题模型。

运用情况

该模型常用于解决与序列相关的优化问题，例如在一个数字序列中找到最长的递增子序列。
它可以应用于各种领域，如计算机科学、数学、生物学等。

注意事项

定义明确的状态表示：确保状态能够准确地描述问题的特征。
正确的状态转移方程：根据问题的逻辑，推导出合理的状态转移方程。
边界情况的处理：考虑序列的起始和结束位置，以及特殊情况的处理。
子序列不要求连续：最长上升子序列中的元素不一定是原始序列中连续的元素。
可能存在多个最长上升子序列：一个序列可能有多个长度相同的最长上升子序列。
算法效率：求解最长上升子序列的算法有多种，不同算法的时间复杂度和空间复杂度可能不同。

解题思路

定义状态：一般使用一个一维或二维数组来表示状态。
建立状态转移方程：根据问题的要求，确定如何从一个状态转移到另一个状态。
初始化状态：设置初始值，通常为边界情况或基本情况。
按照状态转移方程进行计算：通过迭代或递归的方式，根据已知状态计算出其他状态的值。
最终答案的确定：根据问题的要求，从最终的状态中得出答案。
动态规划 ：这是一种常见的解决最长上升子序列问题的方法。通过维护一个辅助数组dp，其中dp[i]表示以第i个元素结尾的最长上升子序列的长度。然后，根据当前元素与之前元素的关系，更新dp数组的值。
二分查找：在一些情况下，可以使用二分查找来优化动态规划的过程，提高算法效率。
其他方法：除了动态规划，还可以使用其他方法来解决最长上升子序列问题，如贪心算法、分治算法等。

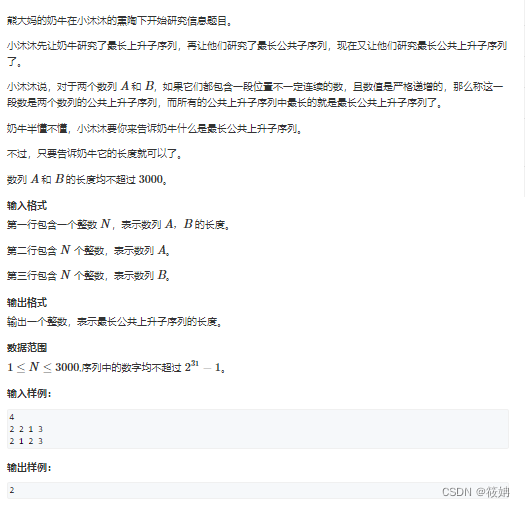
AcWing 272. 最长公共上升子序列

题目描述

AcWing 272. 最长公共上升子序列 - AcWing

运行代码

cpp 复制代码

#include <iostream>
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main()
{
     cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];
    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);

            if (b[j] < a[i])
                maxv = max(maxv, f[i - 1][j] + 1);
        }
    }
    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;
    return 0;
}

代码思路

定义了常量 N 表示序列的最大长度。
输入两个序列 a 和 b 的长度 n 以及它们各自的元素。
f[i][j] 表示以 a 的前 i 个元素和 b 的前 j 个元素中最长公共上升子序列的长度。
外层循环遍历 a 的元素。对于每个 i：
- 先初始化一个变量 maxv 为 1。
- 内层循环遍历 b 的元素。对于每个 j：
  - 首先将 f[i][j] 更新为上一行（即 i-1 行）对应位置的值，这是一种继承。
  - 如果当前 a[i] 等于 b[j]，则更新 f[i][j] 为当前的 maxv，因为找到了一个公共上升元素。
  - 如果 b[j] 小于 a[i]，则更新 maxv 为当前 maxv 和上一行对应位置值加 1 中的较大值，这是在计算以当前 b[j] 结尾的可能的更长的公共上升子序列长度。
最后通过遍历 f[n][i] 找到整个数组中的最大值，即最长公共上升子序列的长度并输出。

改进思路

空间优化 ：可以观察到在计算 f[i][j] 时，实际上只用到了上一行的数据，所以可以考虑使用滚动数组来优化空间，将空间复杂度从 O(n^2) 降低到 O(n)。
利用二分查找 ：在更新 maxv 时，可以考虑使用二分查找来更高效地找到满足条件的位置，而不是简单地线性遍历。
预处理一些信息 ：比如可以预先计算 b 序列中每个元素之前比它小的元素的个数等信息，以便在计算过程中能更快地做出判断和更新。