大家好,今天我们来深入学习《算法导论》第 12 章的内容 ------ 二叉搜索树(Binary Search Tree, BST)。二叉搜索树是一种经典的数据结构,它结合了链表的动态性和有序数组的高效查询能力,在实际开发中有着广泛的应用。
本文将按照《算法导论》的章节结构,详细讲解二叉搜索树的定义、查询、插入、删除等操作,并提供完整可运行的 C++ 代码实现,帮助大家更好地理解和实践。
12.1 什么是二叉搜索树
12.1.1 二叉搜索树的定义
二叉搜索树是一种二叉树,它可以为空,或者满足以下性质:
- 设
x是二叉搜索树中的一个节点。如果y是x左子树中的一个节点,那么y.key <= x.key - 如果
y是x右子树中的一个节点,那么y.key >= x.key
简单来说,就是左子树所有节点的值不大于根节点的值,右子树所有节点的值不小于根节点的值,并且这个性质对树中的每个节点都成立。
12.1.2 二叉搜索树的示例
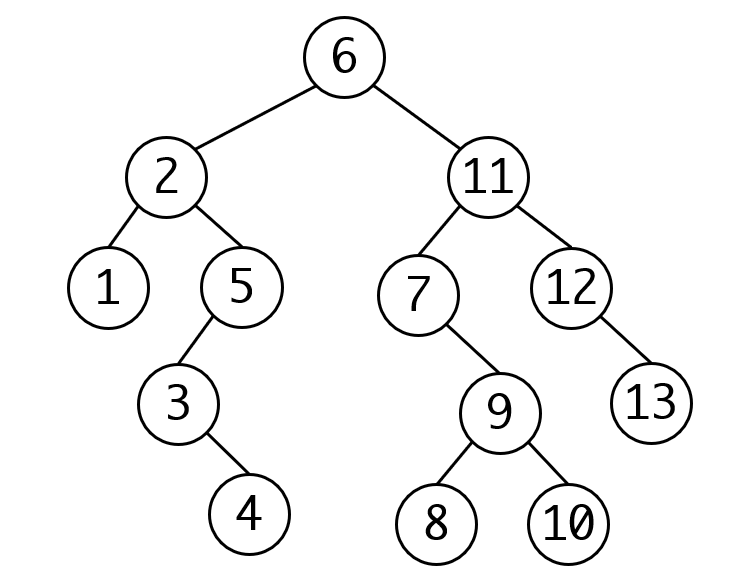
下面是一个二叉搜索树的示例:
15
/ \
6 18
/ \ /
3 7 17
/ \ \
2 4 13
/
9在这个树中,每个节点的左子树都满足所有节点值小于该节点值,右子树所有节点值大于该节点值。
12.1.3 二叉搜索树的特性
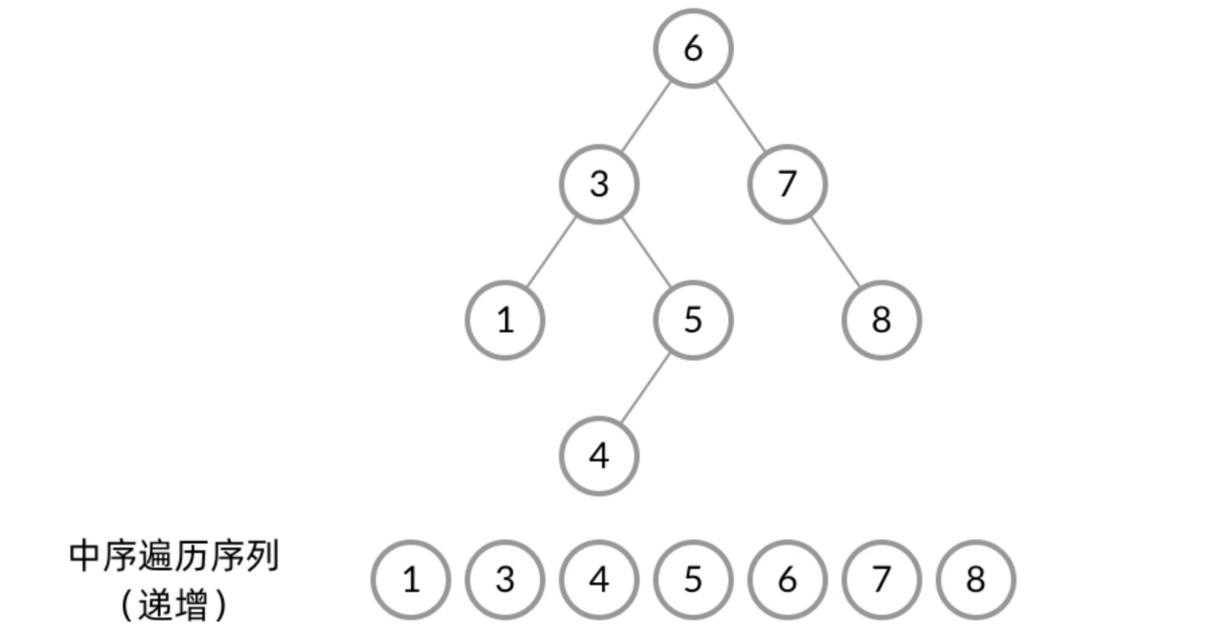
二叉搜索树的最重要特性是中序遍历(左 - 根 - 右)可以得到一个按升序排列的节点序列。
例如,对上面的示例树进行中序遍历,得到的序列是:2, 3, 4, 6, 7, 9, 13, 15, 17, 18,这是一个升序序列。
12.1.4 二叉搜索树的思维导图
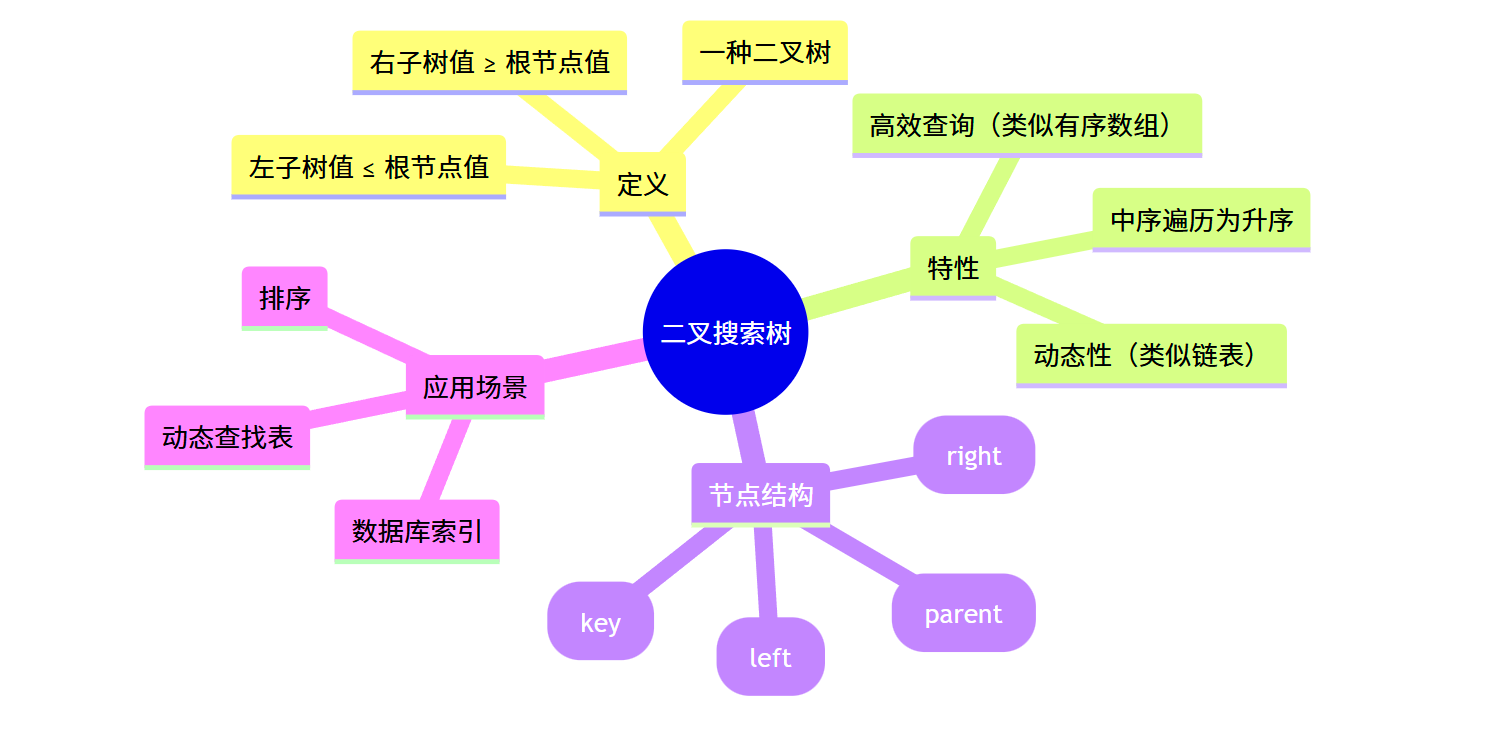
12.2 查询二叉搜索树
二叉搜索树的查询操作是其最基本也最重要的操作之一,主要包括:查找特定值、查找最小值、查找最大值、查找前驱和后继。
12.2.1 查找(Search)
查找操作用于在二叉搜索树中查找一个具有特定关键字的节点。
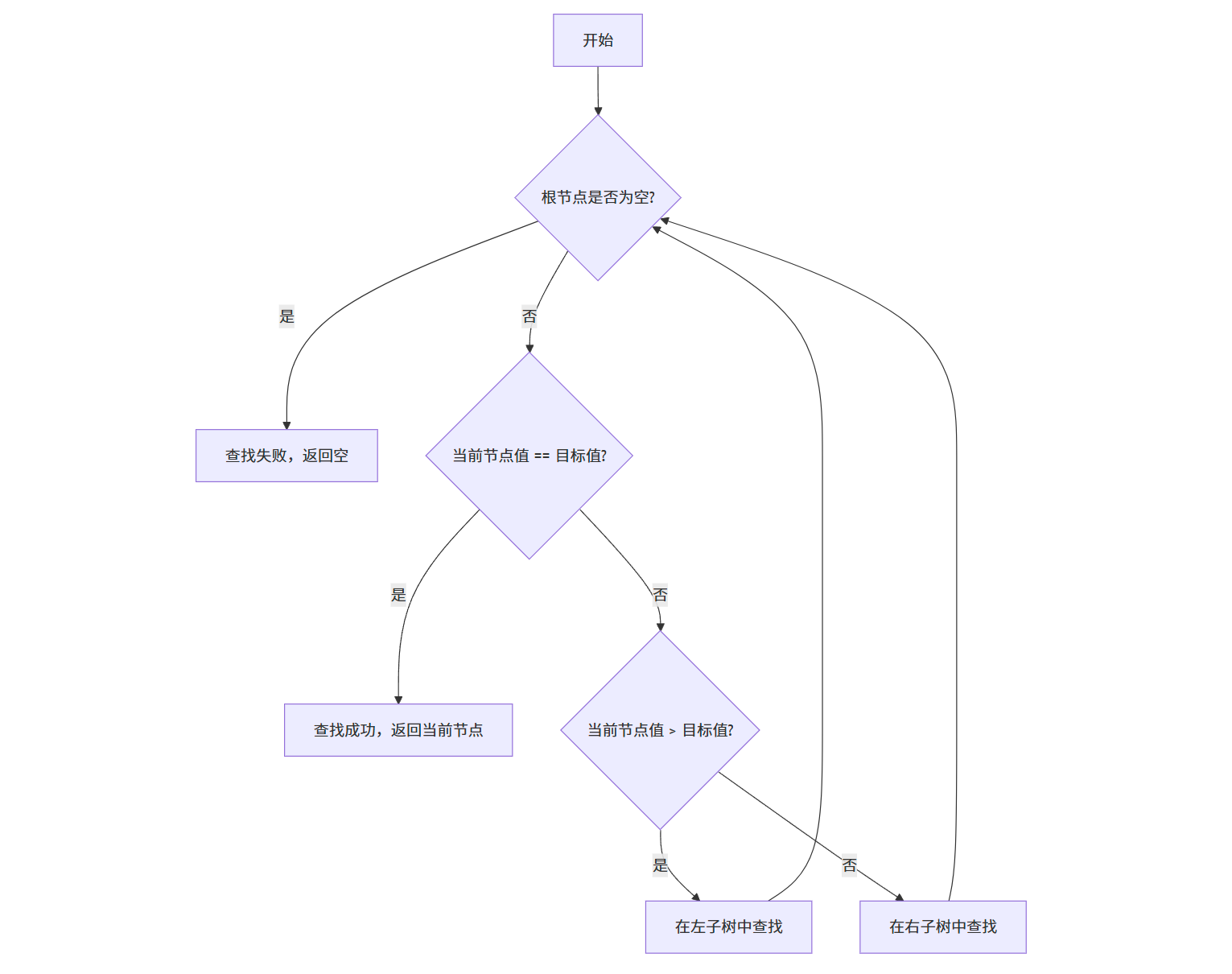
算法思想:
- 从根节点开始
- 如果当前节点为空,说明查找失败
- 如果当前节点的关键字等于目标值,查找成功
- 如果当前节点的关键字大于目标值,在左子树中查找
- 如果当前节点的关键字小于目标值,在右子树中查找
流程图:
12.2.2 查找最小值(Minimum)
最小值节点是二叉搜索树中最左侧的节点(即左子树为空的节点)。
算法思想:
- 从根节点开始
- 沿着左子树指针一直向下
- 直到找到一个左子树为空的节点,该节点即为最小值节点
12.2.3 查找最大值(Maximum)
最大值节点是二叉搜索树中最右侧的节点(即右子树为空的节点)。
算法思想:
- 从根节点开始
- 沿着右子树指针一直向下
- 直到找到一个右子树为空的节点,该节点即为最大值节点
12.2.4 查找前驱(Predecessor)
前驱是指在中序遍历中,位于当前节点之前的节点(即比当前节点小的最大节点)。
算法思想:
- 如果当前节点有左子树,则前驱是左子树中的最大值节点
- 否则,向上查找祖先节点,直到找到一个节点是其父节点的右孩子,该父节点即为前驱
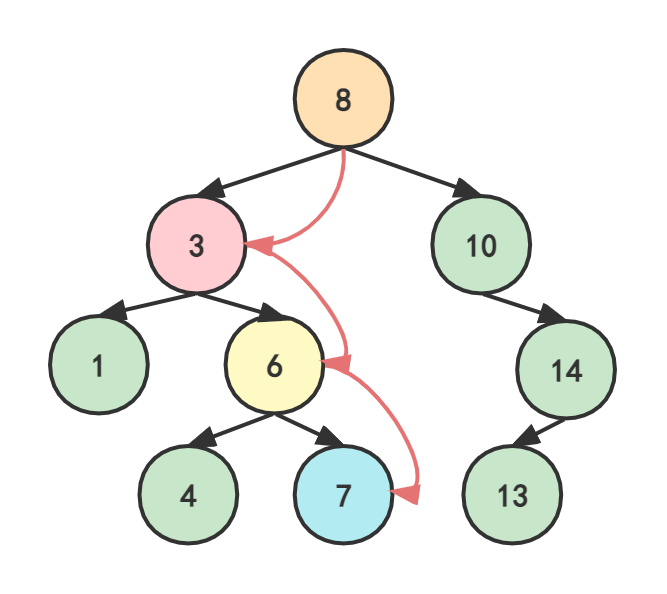
12.2.5 查找后继(Successor)
后继是指在中序遍历中,位于当前节点之后的节点(即比当前节点大的最小节点)。
算法思想:
- 如果当前节点有右子树,则后继是右子树中的最小值节点
- 否则,向上查找祖先节点,直到找到一个节点是其父节点的左孩子,该父节点即为后继
12.2.6 查询操作的代码实现
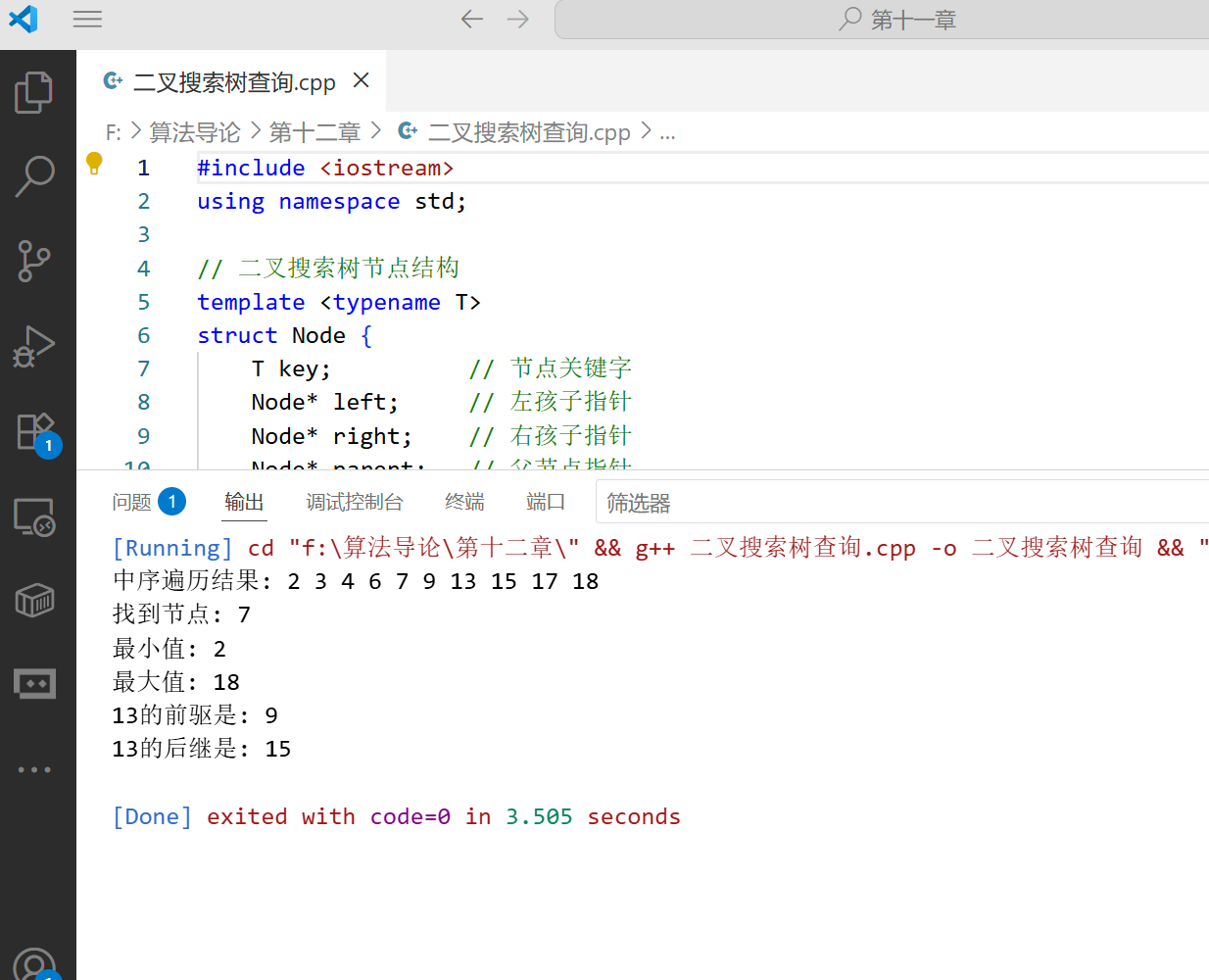
下面是二叉搜索树查询操作的完整 C++ 实现:
cpp
#include <iostream>
using namespace std;
// 二叉搜索树节点结构
template <typename T>
struct Node {
T key; // 节点关键字
Node* left; // 左孩子指针
Node* right; // 右孩子指针
Node* parent; // 父节点指针
// 构造函数
Node(T val) : key(val), left(nullptr), right(nullptr), parent(nullptr) {}
};
// 二叉搜索树类
template <typename T>
class BST {
private:
Node<T>* root; // 根节点指针
// 递归查找
Node<T>* search(Node<T>* x, T val) {
// 如果节点为空或找到目标值,返回该节点
if (x == nullptr || x->key == val) {
return x;
}
// 如果目标值小于当前节点值,在左子树中查找
if (val < x->key) {
return search(x->left, val);
}
// 否则在右子树中查找
else {
return search(x->right, val);
}
}
// 查找最小值
Node<T>* minimum(Node<T>* x) {
// 一直向左查找,直到左子树为空
while (x != nullptr && x->left != nullptr) {
x = x->left;
}
return x;
}
// 查找最大值
Node<T>* maximum(Node<T>* x) {
// 一直向右查找,直到右子树为空
while (x != nullptr && x->right != nullptr) {
x = x->right;
}
return x;
}
// 私有版本的查找前驱
Node<T>* predecessorHelper(Node<T>* x) {
// 如果有左子树,前驱是左子树的最大值
if (x->left != nullptr) {
return maximum(x->left);
}
// 否则向上查找
Node<T>* y = x->parent;
while (y != nullptr && x == y->left) {
x = y;
y = y->parent;
}
return y;
}
// 私有版本的查找后继
Node<T>* successorHelper(Node<T>* x) {
// 如果有右子树,后继是右子树的最小值
if (x->right != nullptr) {
return minimum(x->right);
}
// 否则向上查找
Node<T>* y = x->parent;
while (y != nullptr && x == y->right) {
x = y;
y = y->parent;
}
return y;
}
// 中序遍历
void inorderTraversal(Node<T>* x) {
if (x != nullptr) {
inorderTraversal(x->left); // 遍历左子树
cout << x->key << " "; // 访问当前节点
inorderTraversal(x->right); // 遍历右子树
}
}
public:
// 构造函数
BST() : root(nullptr) {}
// 查找操作
Node<T>* search(T val) {
return search(root, val);
}
// 查找最小值
Node<T>* minimum() {
return minimum(root);
}
// 查找最大值
Node<T>* maximum() {
return maximum(root);
}
// 查找前驱
Node<T>* predecessor(Node<T>* x) {
if (x == nullptr) return nullptr;
return predecessorHelper(x);
}
// 查找后继
Node<T>* successor(Node<T>* x) {
if (x == nullptr) return nullptr;
return successorHelper(x);
}
// 中序遍历
void inorderTraversal() {
inorderTraversal(root);
cout << endl;
}
// 设置根节点(用于测试)
void setRoot(Node<T>* r) {
root = r;
}
};
// 测试代码
int main() {
BST<int> bst;
// 手动构建一个示例树
// 15
// / \
// 6 18
// / \ /
// 3 7 17
// / \ \
// 2 4 13
// /
// 9
Node<int>* node15 = new Node<int>(15);
Node<int>* node6 = new Node<int>(6);
Node<int>* node18 = new Node<int>(18);
Node<int>* node3 = new Node<int>(3);
Node<int>* node7 = new Node<int>(7);
Node<int>* node17 = new Node<int>(17);
Node<int>* node2 = new Node<int>(2);
Node<int>* node4 = new Node<int>(4);
Node<int>* node13 = new Node<int>(13);
Node<int>* node9 = new Node<int>(9);
// 设置根节点
bst.setRoot(node15);
// 构建树结构
node15->left = node6;
node15->right = node18;
node6->parent = node15;
node18->parent = node15;
node6->left = node3;
node6->right = node7;
node3->parent = node6;
node7->parent = node6;
node18->left = node17;
node17->parent = node18;
node3->left = node2;
node3->right = node4;
node2->parent = node3;
node4->parent = node3;
node7->right = node13;
node13->parent = node7;
node13->left = node9;
node9->parent = node13;
// 演示中序遍历(应输出升序序列)
cout << "中序遍历结果: ";
bst.inorderTraversal();
// 演示查找操作
int target = 7;
Node<int>* found = bst.search(target);
if (found != nullptr) {
cout << "找到节点: " << found->key << endl;
} else {
cout << "未找到节点: " << target << endl;
}
// 演示查找最小值和最大值
Node<int>* minNode = bst.minimum();
Node<int>* maxNode = bst.maximum();
cout << "最小值: " << minNode->key << endl;
cout << "最大值: " << maxNode->key << endl;
// 演示查找前驱和后继
Node<int>* x = bst.search(13);
if (x != nullptr) {
Node<int>* pred = bst.predecessor(x);
Node<int>* succ = bst.successor(x);
cout << x->key << "的前驱是: " << (pred ? pred->key : -1) << endl;
cout << x->key << "的后继是: " << (succ ? succ->key : -1) << endl;
}
// 释放内存
delete node2;
delete node3;
delete node4;
delete node6;
delete node7;
delete node9;
delete node13;
delete node15;
delete node17;
delete node18;
return 0;
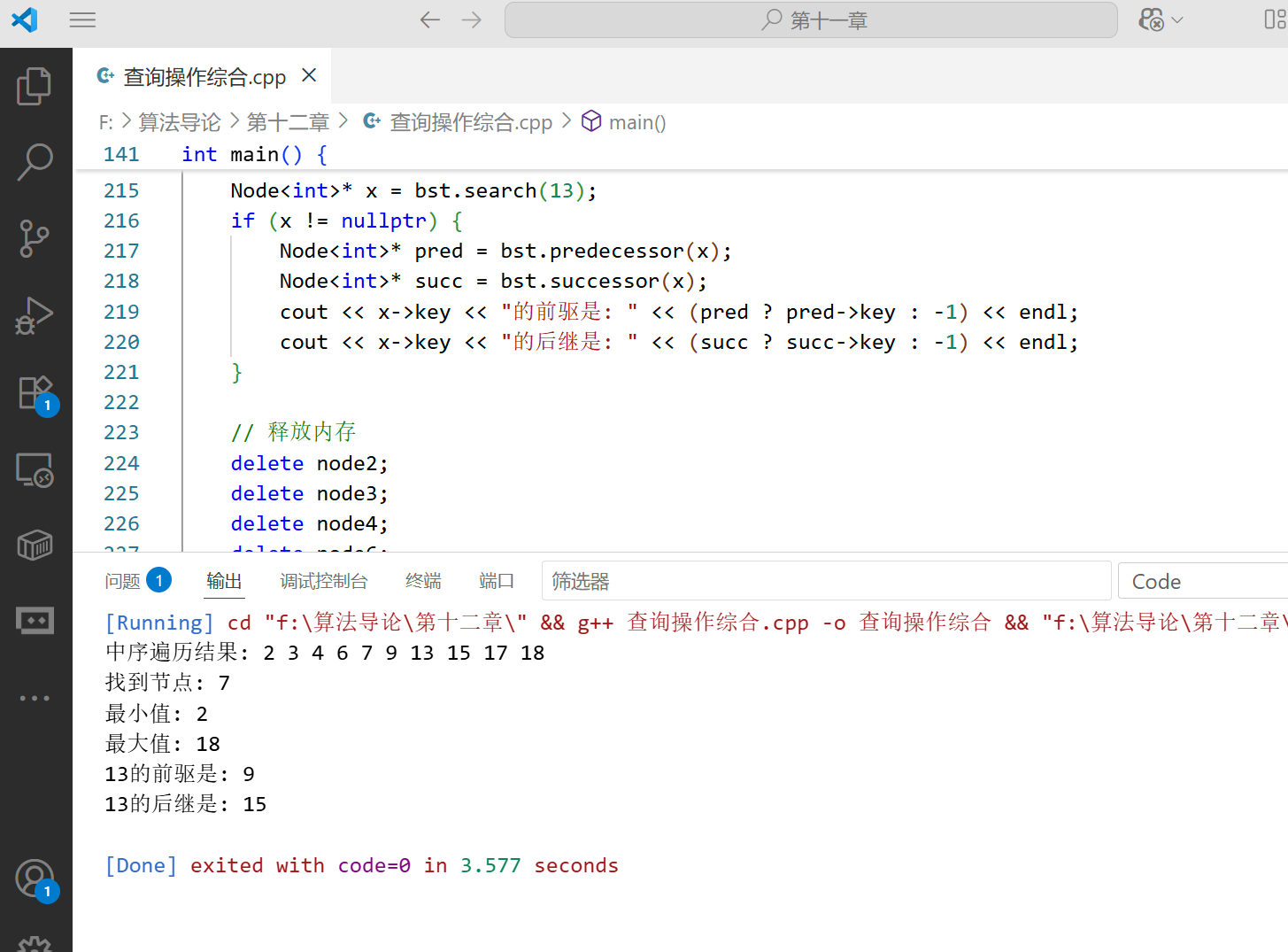
}12.2.7 查询操作的综合案例
下面是一个演示二叉搜索树查询操作的综合案例:
cpp
#include <iostream>
using namespace std;
// 二叉搜索树节点结构
template <typename T>
struct Node {
T key; // 节点关键字
Node* left; // 左孩子指针
Node* right; // 右孩子指针
Node* parent; // 父节点指针
// 构造函数
Node(T val) : key(val), left(nullptr), right(nullptr), parent(nullptr) {}
};
// 二叉搜索树类
template <typename T>
class BST {
private:
Node<T>* root; // 根节点指针
// 递归查找
Node<T>* search(Node<T>* x, T val) {
// 如果节点为空或找到目标值,返回该节点
if (x == nullptr || x->key == val) {
return x;
}
// 如果目标值小于当前节点值,在左子树中查找
if (val < x->key) {
return search(x->left, val);
}
// 否则在右子树中查找
else {
return search(x->right, val);
}
}
// 查找最小值
Node<T>* minimum(Node<T>* x) {
// 一直向左查找,直到左子树为空
while (x != nullptr && x->left != nullptr) {
x = x->left;
}
return x;
}
// 查找最大值
Node<T>* maximum(Node<T>* x) {
// 一直向右查找,直到右子树为空
while (x != nullptr && x->right != nullptr) {
x = x->right;
}
return x;
}
// 私有版本的查找前驱
Node<T>* predecessorHelper(Node<T>* x) {
// 如果有左子树,前驱是左子树的最大值
if (x->left != nullptr) {
return maximum(x->left);
}
// 否则向上查找
Node<T>* y = x->parent;
while (y != nullptr && x == y->left) {
x = y;
y = y->parent;
}
return y;
}
// 私有版本的查找后继
Node<T>* successorHelper(Node<T>* x) {
// 如果有右子树,后继是右子树的最小值
if (x->right != nullptr) {
return minimum(x->right);
}
// 否则向上查找
Node<T>* y = x->parent;
while (y != nullptr && x == y->right) {
x = y;
y = y->parent;
}
return y;
}
// 中序遍历
void inorderTraversal(Node<T>* x) {
if (x != nullptr) {
inorderTraversal(x->left); // 遍历左子树
cout << x->key << " "; // 访问当前节点
inorderTraversal(x->right); // 遍历右子树
}
}
public:
// 构造函数
BST() : root(nullptr) {}
// 查找操作
Node<T>* search(T val) {
return search(root, val);
}
// 查找最小值
Node<T>* minimum() {
return minimum(root);
}
// 查找最大值
Node<T>* maximum() {
return maximum(root);
}
// 查找前驱
Node<T>* predecessor(Node<T>* x) {
if (x == nullptr) return nullptr;
return predecessorHelper(x);
}
// 查找后继
Node<T>* successor(Node<T>* x) {
if (x == nullptr) return nullptr;
return successorHelper(x);
}
// 中序遍历
void inorderTraversal() {
inorderTraversal(root);
cout << endl;
}
// 设置根节点(用于测试)
void setRoot(Node<T>* r) {
root = r;
}
};
// 查询操作综合案例
int main() {
// 创建一个二叉搜索树并手动插入节点
BST<int> bst;
// 手动构建一个示例树
// 15
// / \
// 6 18
// / \ /
// 3 7 17
// / \ \
// 2 4 13
// /
// 9
Node<int>* node15 = new Node<int>(15);
Node<int>* node6 = new Node<int>(6);
Node<int>* node18 = new Node<int>(18);
Node<int>* node3 = new Node<int>(3);
Node<int>* node7 = new Node<int>(7);
Node<int>* node17 = new Node<int>(17);
Node<int>* node2 = new Node<int>(2);
Node<int>* node4 = new Node<int>(4);
Node<int>* node13 = new Node<int>(13);
Node<int>* node9 = new Node<int>(9);
// 设置根节点
bst.setRoot(node15);
// 构建树结构
node15->left = node6;
node15->right = node18;
node6->parent = node15;
node18->parent = node15;
node6->left = node3;
node6->right = node7;
node3->parent = node6;
node7->parent = node6;
node18->left = node17;
node17->parent = node18;
node3->left = node2;
node3->right = node4;
node2->parent = node3;
node4->parent = node3;
node7->right = node13;
node13->parent = node7;
node13->left = node9;
node9->parent = node13;
// 演示中序遍历(应输出升序序列)
cout << "中序遍历结果: ";
bst.inorderTraversal();
// 演示查找操作
int target = 7;
Node<int>* found = bst.search(target);
if (found != nullptr) {
cout << "找到节点: " << found->key << endl;
} else {
cout << "未找到节点: " << target << endl;
}
// 演示查找最小值和最大值
Node<int>* minNode = bst.minimum();
Node<int>* maxNode = bst.maximum();
cout << "最小值: " << minNode->key << endl;
cout << "最大值: " << maxNode->key << endl;
// 演示查找前驱和后继
Node<int>* x = bst.search(13);
if (x != nullptr) {
Node<int>* pred = bst.predecessor(x);
Node<int>* succ = bst.successor(x);
cout << x->key << "的前驱是: " << (pred ? pred->key : -1) << endl;
cout << x->key << "的后继是: " << (succ ? succ->key : -1) << endl;
}
// 释放内存
delete node2;
delete node3;
delete node4;
delete node6;
delete node7;
delete node9;
delete node13;
delete node15;
delete node17;
delete node18;
return 0;
}
注意:为了使上述代码能够运行,需要在 BST 类中添加一个
setRoot方法用于设置根节点,代码如下:
// 在BST类的public部分添加 void setRoot(Node<T>* r) { root = r; }
12.3 插入和删除
除了查询操作,插入和删除也是二叉搜索树的基本操作。
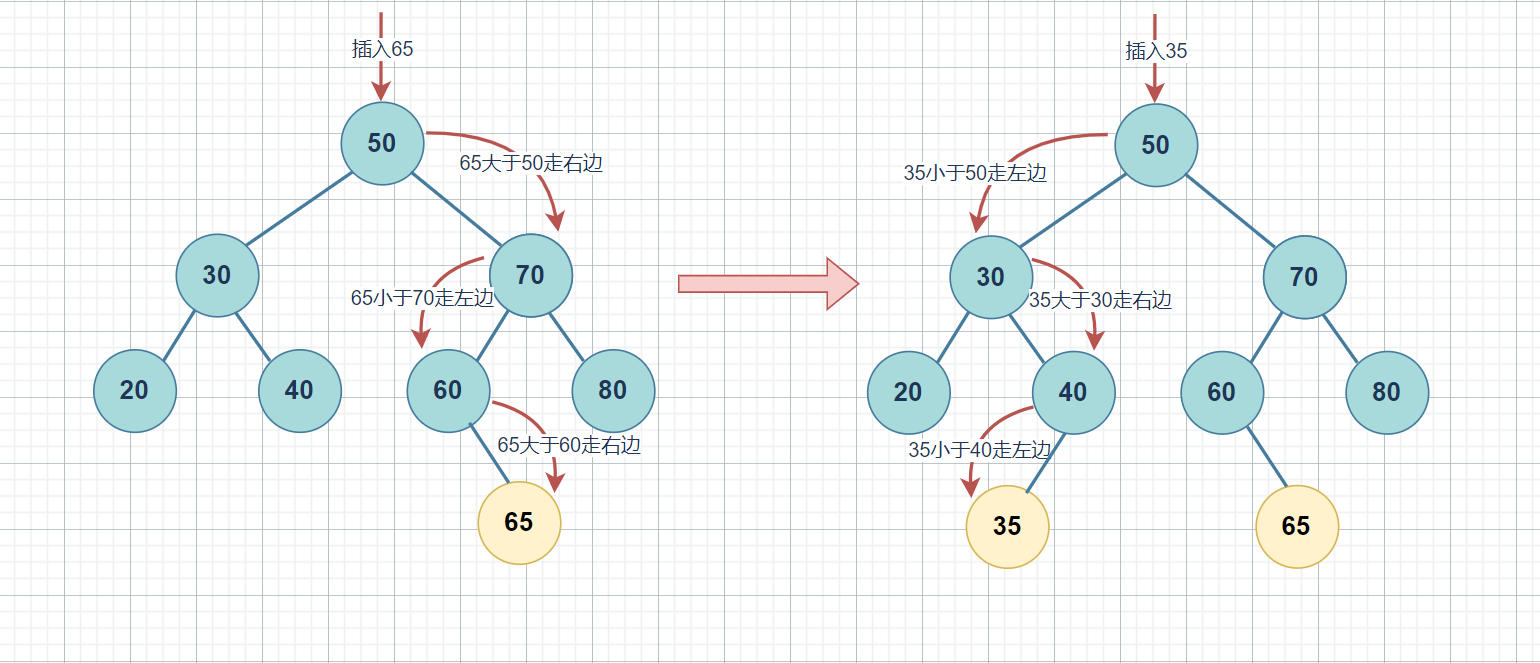
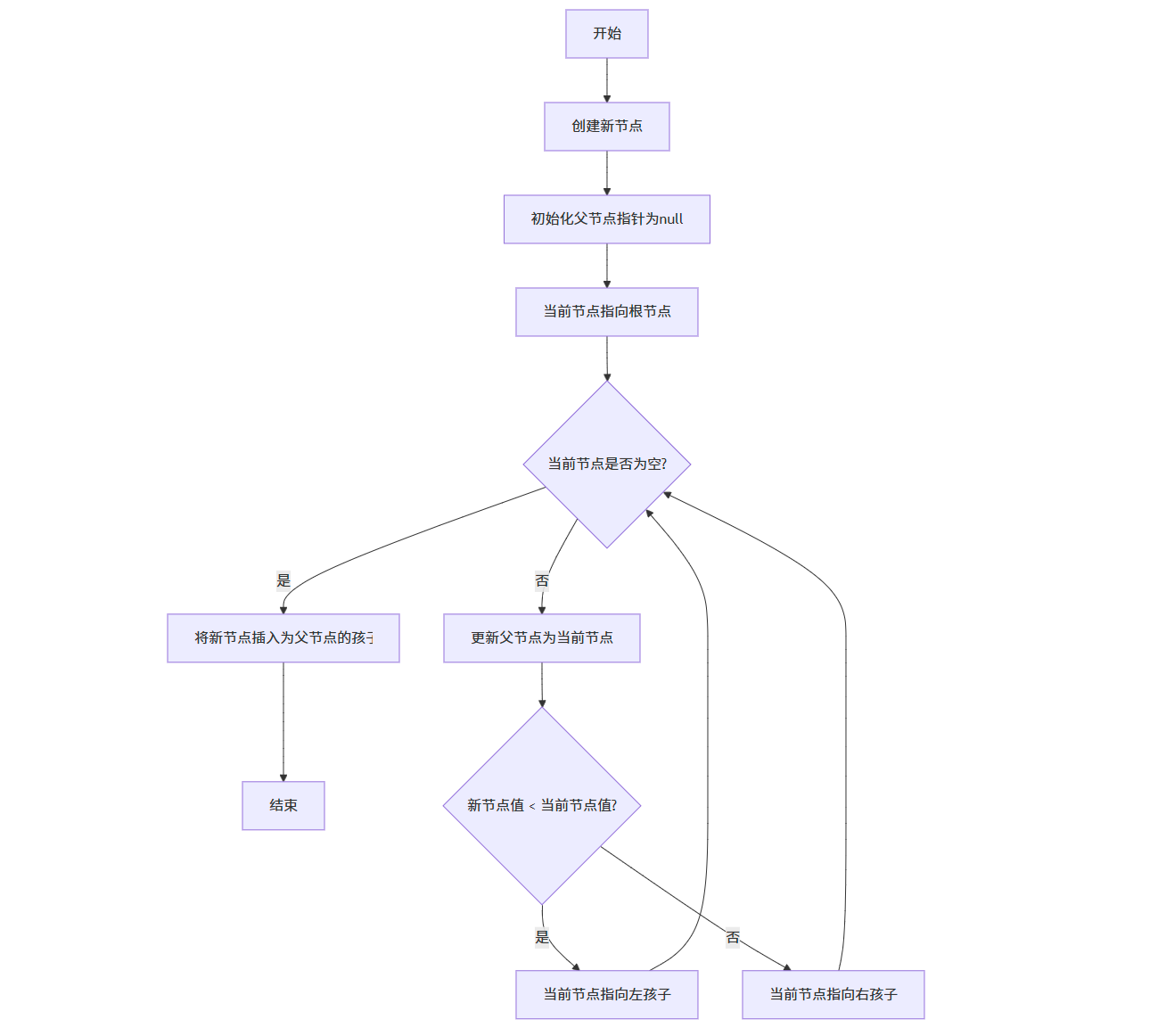
12.3.1 插入(Insert)
插入操作用于在二叉搜索树中插入一个新节点,同时保持二叉搜索树的性质。
算法思想:
- 从根节点开始,找到新节点的合适插入位置
- 新节点总是作为叶子节点插入
- 插入过程与查找过程类似,只是需要记录插入位置的父节点
流程图:
12.3.2 删除(Delete)
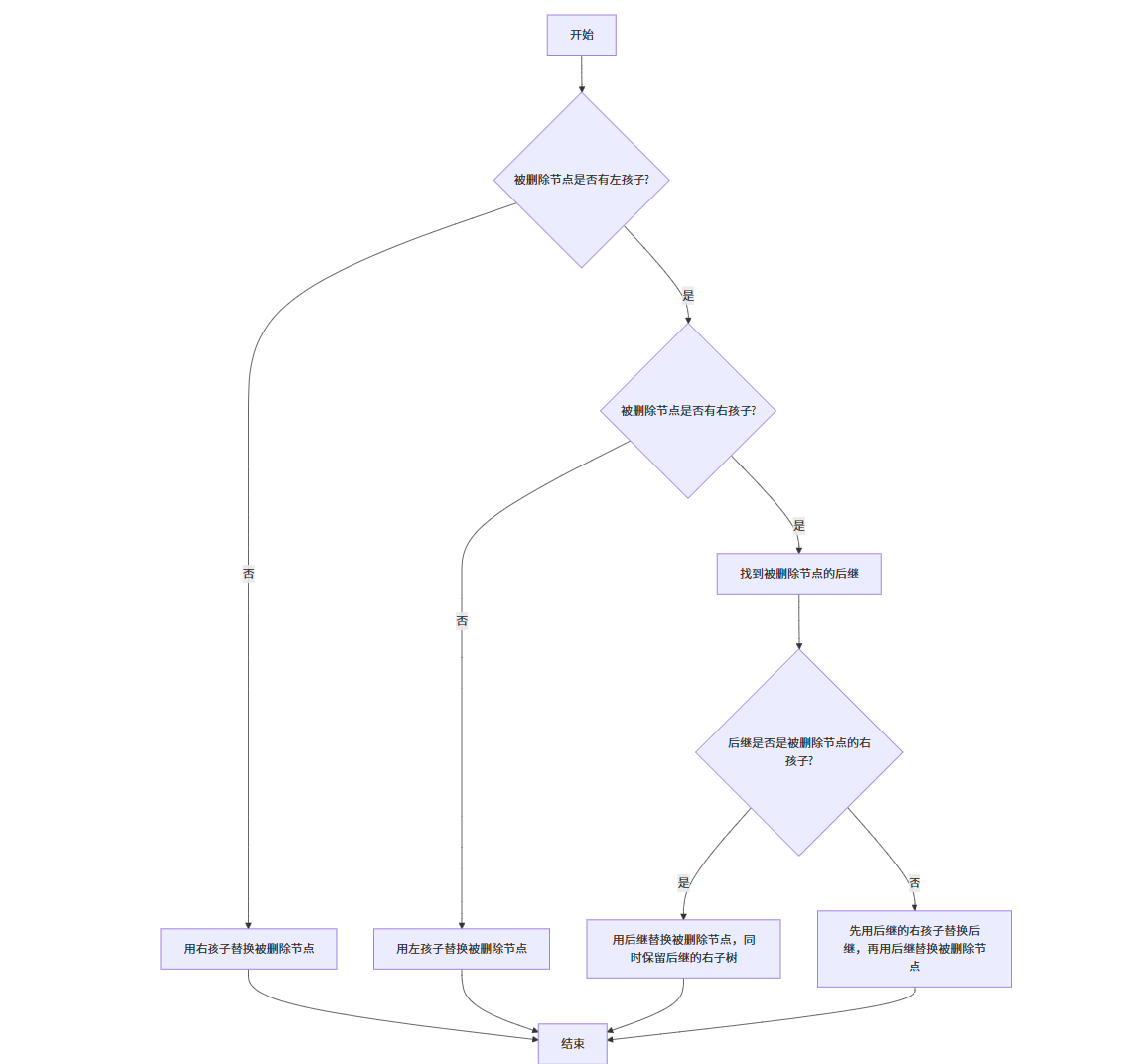
删除操作相对复杂,需要考虑多种情况,同时保持二叉搜索树的性质。
算法思想:
- 如果被删除节点没有孩子,直接删除
- 如果被删除节点只有一个孩子,用孩子替换该节点
- 如果被删除节点有两个孩子,找到该节点的后继(或前驱),用后继替换该节点,然后删除后继
为了简化删除操作,《算法导论》中引入了一个辅助函数transplant,用于将一棵子树替换为另一棵子树。
流程图:
12.3.3 插入和删除操作的代码实现
下面是在 BST 类中添加插入和删除操作的代码:
// 在BST类的public部分添加
// 插入操作
void insert(T val) {
Node<T>* z = new Node<T>(val);
insert(z);
}
// 删除操作
void remove(Node<T>* z) {
if (z == nullptr) return;
// 情况1:没有左孩子
if (z->left == nullptr) {
transplant(z, z->right);
}
// 情况2:有左孩子但没有右孩子
else if (z->right == nullptr) {
transplant(z, z->left);
}
// 情况3:有两个孩子
else {
Node<T>* y = minimum(z->right); // 找到后继
// 如果后继不是直接右孩子
if (y->parent != z) {
transplant(y, y->right); // 用后继的右孩子替换后继
y->right = z->right; // 后继的右指针指向z的右孩子
y->right->parent = y;
}
transplant(z, y); // 用后继替换z
y->left = z->left; // 后继的左指针指向z的左孩子
y->left->parent = y;
}
delete z; // 释放被删除节点的内存
}
// 在BST类的private部分添加
// 插入操作
void insert(Node<T>* z) {
Node<T>* y = nullptr; // 记录x的父节点
Node<T>* x = root; // 从根节点开始
// 找到插入位置
while (x != nullptr) {
y = x; // 更新父节点
if (z->key < x->key) { // 比较关键字,决定向左还是向右
x = x->left;
} else {
x = x->right;
}
}
z->parent = y; // 设置z的父节点
// 如果树为空,z成为根节点
if (y == nullptr) {
root = z;
}
// 否则根据关键字大小插入到左或右
else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
}
// 替换子树辅助函数
void transplant(Node<T>* u, Node<T>* v) {
// 如果u是根节点,v成为新的根节点
if (u->parent == nullptr) {
root = v;
}
// 如果u是左孩子,v成为其父节点的新左孩子
else if (u == u->parent->left) {
u->parent->left = v;
}
// 否则v成为其父节点的新右孩子
else {
u->parent->right = v;
}
// 如果v不为空,更新其父节点指针
if (v != nullptr) {
v->parent = u->parent;
}
}12.3.4 插入和删除操作的综合案例
下面是一个演示二叉搜索树插入和删除操作的综合案例:
// 插入和删除操作综合案例
int main() {
BST<int> bst;
// 插入节点
int values[] = {15, 6, 18, 3, 7, 17, 2, 4, 13, 9};
int n = sizeof(values) / sizeof(values[0]);
cout << "插入顺序: ";
for (int i = 0; i < n; i++) {
cout << values[i] << " ";
bst.insert(values[i]);
}
cout << endl;
cout << "插入后的中序遍历: ";
bst.inorderTraversal();
// 测试删除操作
// 删除叶子节点(4)
Node<int>* node4 = bst.search(4);
if (node4 != nullptr) {
bst.remove(node4);
cout << "删除4后的中序遍历: ";
bst.inorderTraversal();
}
// 删除只有一个孩子的节点(7)
Node<int>* node7 = bst.search(7);
if (node7 != nullptr) {
bst.remove(node7);
cout << "删除7后的中序遍历: ";
bst.inorderTraversal();
}
// 删除有两个孩子的节点(6)
Node<int>* node6 = bst.search(6);
if (node6 != nullptr) {
bst.remove(node6);
cout << "删除6后的中序遍历: ";
bst.inorderTraversal();
}
// 测试插入新节点
bst.insert(8);
cout << "插入8后的中序遍历: ";
bst.inorderTraversal();
return 0;
}12.4 随机构建二叉搜索树
到目前为止,我们讨论的二叉搜索树的性能很大程度上取决于输入数据的顺序。如果输入数据已经排序,那么构建的二叉搜索树将退化为链表,此时各种操作的时间复杂度将变为 O (n)。
为了避免这种情况,我们可以采用随机化方法构建二叉搜索树,即随机排列输入序列,然后再插入到二叉搜索树中。
12.4.1 随机构建二叉搜索树的性质
随机构建的二叉搜索树具有以下重要性质:
- 对于一个包含 n 个不同元素的集合,随机构建的二叉搜索树的期望高度为 O (log n)
- 因此,所有基本操作(查找、插入、删除)的期望时间复杂度均为 O (log n)
12.4.2 随机构建二叉搜索树的代码实现
下面是随机构建二叉搜索树的代码实现:
#include <cstdlib>
#include <ctime>
#include <algorithm>
// 在BST类中添加随机构建函数
public:
// 从数组随机构建二叉搜索树
void buildRandomBST(T arr[], int n) {
// 随机打乱数组
srand(time(nullptr));
random_shuffle(arr, arr + n);
// 清空现有树(简化实现,实际应用中需要完整的删除操作)
root = nullptr;
// 依次插入打乱后的元素
for (int i = 0; i < n; i++) {
insert(arr[i]);
}
}12.4.3 随机构建二叉搜索树的综合案例
下面是一个演示随机构建二叉搜索树的综合案例:
// 随机构建二叉搜索树综合案例
int main() {
BST<int> bst;
// 创建一个有序数组
const int n = 10;
int arr[n];
for (int i = 0; i < n; i++) {
arr[i] = i + 1;
}
cout << "原始有序数组: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
// 随机构建二叉搜索树
bst.buildRandomBST(arr, n);
cout << "随机构建的BST中序遍历: ";
bst.inorderTraversal();
// 查找最大值和最小值
Node<int>* minNode = bst.minimum();
Node<int>* maxNode = bst.maximum();
cout << "最小值: " << minNode->key << endl;
cout << "最大值: " << maxNode->key << endl;
// 查找特定值
int target = 5;
Node<int>* found = bst.search(target);
if (found != nullptr) {
cout << "找到节点: " << found->key << endl;
Node<int>* pred = bst.predecessor(found);
Node<int>* succ = bst.successor(found);
cout << target << "的前驱是: " << (pred ? pred->key : -1) << endl;
cout << target << "的后继是: " << (succ ? succ->key : -1) << endl;
} else {
cout << "未找到节点: " << target << endl;
}
return 0;
}思考题
-
证明:在二叉搜索树中,一个节点的前驱节点的关键字一定小于该节点的关键字,后继节点的关键字一定大于该节点的关键字。
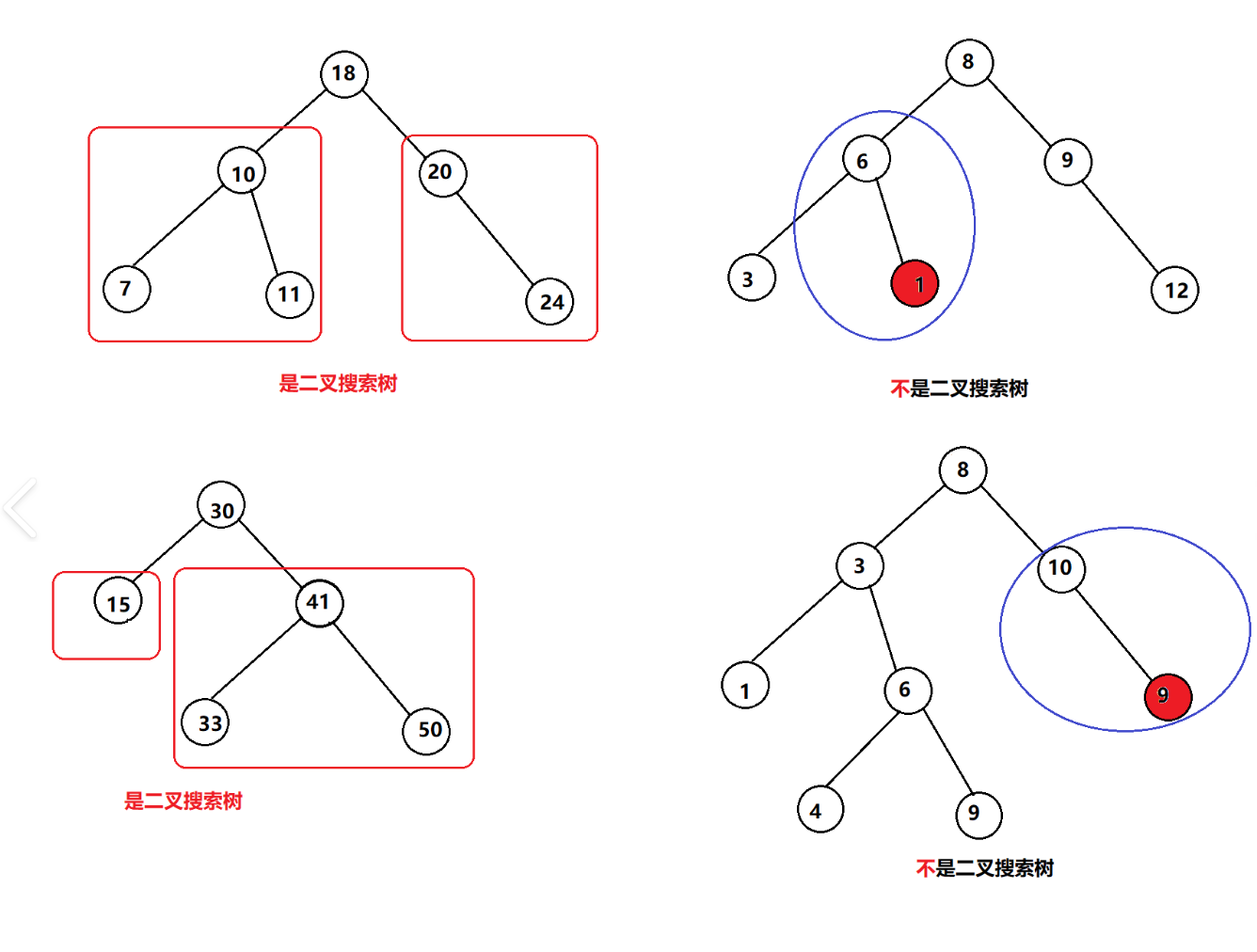
-
设计一个算法,判断一棵二叉树是否为二叉搜索树。
-
对于 n 个关键字,有多少种不同形态的二叉搜索树?
-
设计一个算法,在 O (n) 时间内将一棵二叉搜索树转换为一个有序链表。
-
假设我们有一个包含 n 个元素的二叉搜索树,设计一个算法,找到第 k 小的元素,要求时间复杂度为 O (h),其中 h 是树的高度。
本章注记
二叉搜索树是计算机科学中最基础也最重要的数据结构之一,它首次由 Perliss 在 1960 年提出。二叉搜索树结合了链表的动态性和有序数组的高效查询能力,是许多复杂数据结构的基础,如红黑树、B 树等。

虽然二叉搜索树的最坏情况时间复杂度为 O (n),但在实际应用中表现良好,尤其是当输入数据具有随机性时。对于需要保证最坏情况性能的场景,可以使用平衡二叉搜索树,如 AVL 树、红黑树等,这些数据结构通过各种旋转操作来维持树的平衡性,确保所有操作的时间复杂度为 O (log n)。

二叉搜索树在数据库索引、编译器设计、操作系统等领域有着广泛的应用。理解二叉搜索树的原理和操作是深入学习更复杂数据结构的基础。