SVM的 核函数 和 超参数 介绍:
机器学习------支持向量机(SVM)-CSDN博客![]() https://blog.csdn.net/2302_78022640/article/details/150073569
https://blog.csdn.net/2302_78022640/article/details/150073569
支持向量机(SVM)实战案例:鸢尾花部分数据 二分类与决策边界可视化
支持向量机(Support Vector Machine,SVM)是一种常用的监督学习分类算法,核心思想是找到一个能够最大化类别间隔 的超平面,实现数据的分类。本案例将通过鸢尾花数据集(Iris)构建一个二分类模型,并绘制决策边界和支持向量。
1. 数据准备与选择特征
from sklearn.datasets import load_iris
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
# 加载鸢尾花数据集
iris = load_iris()
data = iris.data
target = iris.target
# 只取前两类(setosa 和 versicolor)以及两个特征:花萼长度(0)和花瓣长度(2)
X = data[0:100, [0, 2]]
y = target[0:100]说明:
-
鸢尾花数据集共有 150 个样本、3 个类别(0、1、2)。
-
为了便于二维可视化,这里取前两类(标签 0 和 1),并且只用两个特征(便于画二维平面)。
2. 构建并训练 SVM 模型
# 线性核函数,C=∞ 相当于硬间隔 SVM
model = SVC(kernel='linear', C=float('inf'), random_state=100)
model.fit(X, y)核心参数解释:
-
kernel='linear':使用线性核函数,适用于线性可分的情况。
-
C=float('inf') :惩罚因子 C 越大,对误分类的容忍度越低,这里取无限大相当于硬间隔最大化。
-
random_state:随机种子,保证结果可复现。
3. 数据可视化
# 绘制两类数据的散点图
plt.scatter(X[0:50, 0], X[0:50, 1], c='r', marker='o', label='类别0')
plt.scatter(X[50:100, 0], X[50:100, 1], c='g', marker='+', label='类别1')-
类别 0(红色圆点)
-
类别 1(绿色加号)
4. 绘制决策边界和间隔线
# 获取超平面参数 w 和 b
w = model.coef_[0]
b = model.intercept_[0]
# 决策边界:w1*x1 + w2*x2 + b = 0
x1 = np.linspace(0, 10, 100)
x2 = -(w[0] * x1 + b) / w[1]
# 间隔边界:w1*x1 + w2*x2 + b = ±1
x3 = (1 - (w[0] * x1 + b)) / w[1]
x4 = (-1 - (w[0] * x1 + b)) / w[1]
# 绘制
plt.plot(x1,x2,c='b',label='决策边界')
plt.plot(x1,x3,c='b',linestyle='--',label='间隔边界')
plt.plot(x1,x4,c='b',linestyle='--',label='间隔边界')-
实线:决策边界
-
虚线:两条间隔边界,支持向量位于这两条线上。
5. 标记支持向量
# 获取支持向量
vets = model.support_vectors_
plt.scatter(vets[:, 0], vets[:, 1], s=100, facecolors='none', edgecolors='b', label='支持向量')支持向量是离决策边界最近的样本点,SVM 的优化目标就是最大化这些点到边界的间隔。
model.support_vectors_ 是一个 numpy.ndarray,形状为 (n_support_vectors, n_features)。
每一行就是一个支持向量在训练时使用的特征空间坐标 (即训练时输入给 SVM 的特征,若训练前做过 StandardScaler/PCA 等变换,则这里是变换后的坐标)。
-
vets[:, 0], vets[:, 1]- 取支持向量矩阵的第 0 列和第 1 列作为 x、y 坐标 ------ 前提是数据确实是二维 。若维度 >2,需要先降维(PCA/t-SNE)再画图。
-
s=100- 标记大小,注意:
s表示点的面积(points^2) ,不是半径。s=100比较显眼;需要更大更明显可以改成s=150或s=300。
- 标记大小,注意:
-
facecolors='none'- 使标记内部不填充(空心),这样可以"圈出"点而不遮挡原来的颜色/形状。常用于突出某些点(比如支持向量)。
-
edgecolors='b'- 标记边缘颜色设为蓝色(
'b')。当facecolors='none'且 marker 是可填充(如'o')时,会画成蓝色空心圆。
- 标记边缘颜色设为蓝色(
-
label='支持向量'- 用于图例显示。
6. 显示结果
plt.legend()
plt.show()运行结果:
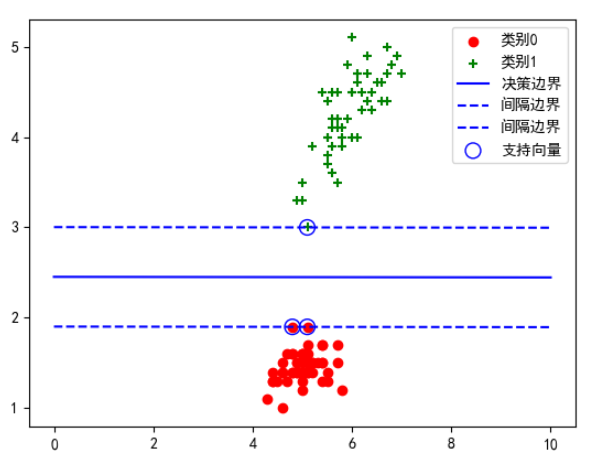
-
红色圆点和绿色加号分别代表两类样本。
-
蓝色实线是决策边界,虚线是最大间隔线。
-
蓝色圈出的点是支持向量。
7. 结果与分析
1. 支持向量(Support Vectors)
-
定义 :支持向量是离分类边界最近的样本点,它们位于最大间隔边界上。
-
作用:
-
唯一决定分类超平面的位置和方向。
-
不是所有样本都会影响分类结果,只有支持向量才会参与优化计算。
-
如果移除非支持向量,模型的分类结果不会变;但如果移除支持向量,边界会发生变化。
-
-
在图中:蓝色圈出来的点,就是支持向量。
2. 决策边界(Decision Boundary)
-
数学形式:
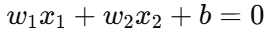
这是模型最终找到的最佳分类超平面,它能最大化两类样本的间隔。
-
作用:
-
处在该线上的点,SVM 判断它们属于哪一类的概率是五五开(分类决策值为 0)。
-
决策边界左侧的点判为一类,右侧的点判为另一类(对于二维空间而言)。
-
-
在图中 :蓝色实线是决策边界。
3. 间隔边界(Margin Boundaries)
-
数学形式:
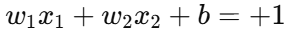
和
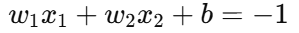
这两条线表示离决策边界等距离的两条平行线。
-
作用:
-
间隔(Margin)是这两条虚线之间的区域,SVM 会努力让这个区域尽可能宽。
-
支持向量正好落在这两条虚线上。
-
-
在图中:
-
蓝色虚线是最大间隔边界。
-
其中一条虚线紧贴类别 0 的支持向量,另一条紧贴类别 1 的支持向量。
-
8. 完整代码
from sklearn.datasets import load_iris
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
iris = load_iris()
data = iris.data
X = data[0:100,[0,2]]
y = iris.target[0:100]
model = SVC(kernel='linear', C=float('inf'), random_state=100)
model.fit(X, y)
plt.scatter(X[0:50,0],X[0:50,1],c='r',marker='o',label='类别0')
plt.scatter(X[50:100,0],X[50:100,1],c='g',marker='+',label='类别1')
w = model.coef_[0]
b = model.intercept_[0]
x1 = np.linspace(0,10,100)
x2 = -(w[0]*x1+b)/w[1]
x3 = (1-(w[0]*x1+b))/w[1]
x4 = (-1-(w[0]*x1+b))/w[1]
plt.plot(x1,x2,c='b',label='决策边界')
plt.plot(x1,x3,c='b',linestyle='--',label='间隔边界')
plt.plot(x1,x4,c='b',linestyle='--',label='间隔边界')
vets = model.support_vectors_
plt.scatter(vets[:,0],vets[:,1],s=100,facecolors='none', edgecolors='b',label='支持向量')
plt.legend()
plt.show()