目录
创作不易,如对您有帮助,还望一键三连,谢谢!
前言
排序在我们日常生活中十分常见,比如:成绩按高低排序,购物网页按价格排序......今天我们就来学习常见的几个排序算法。
学习目标:
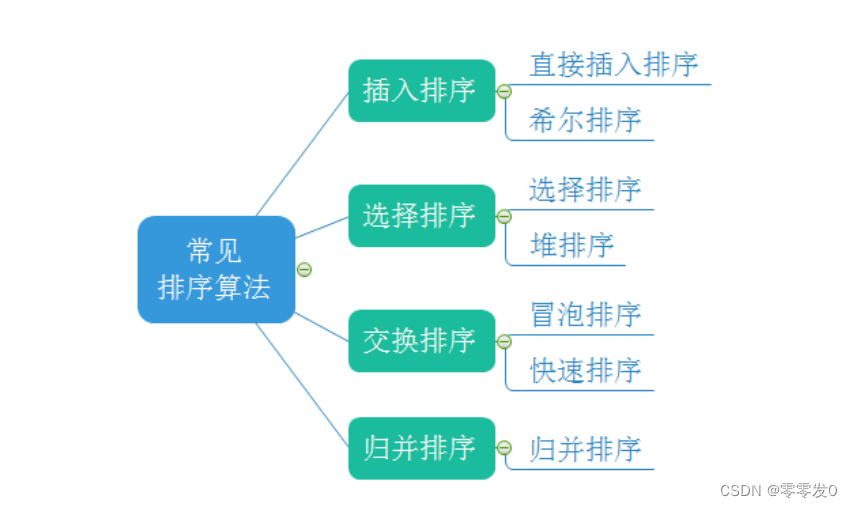
接下来我们一个一个讲解。
直接插入排序
首先,我们先来看动图:
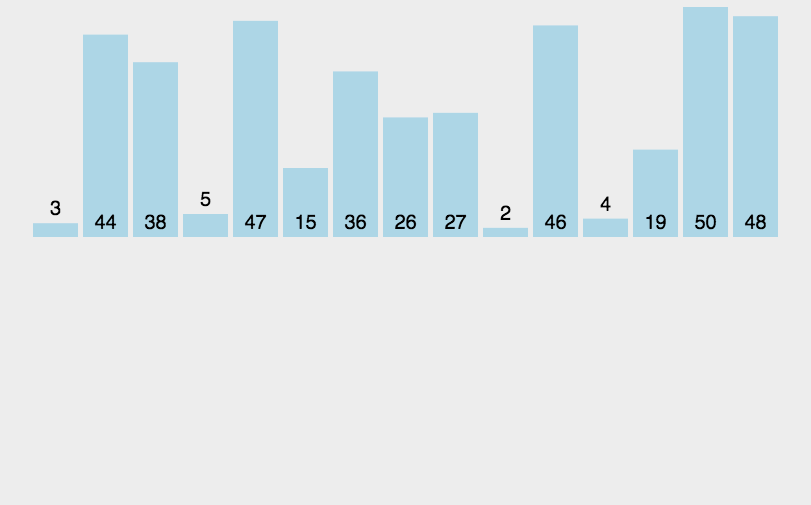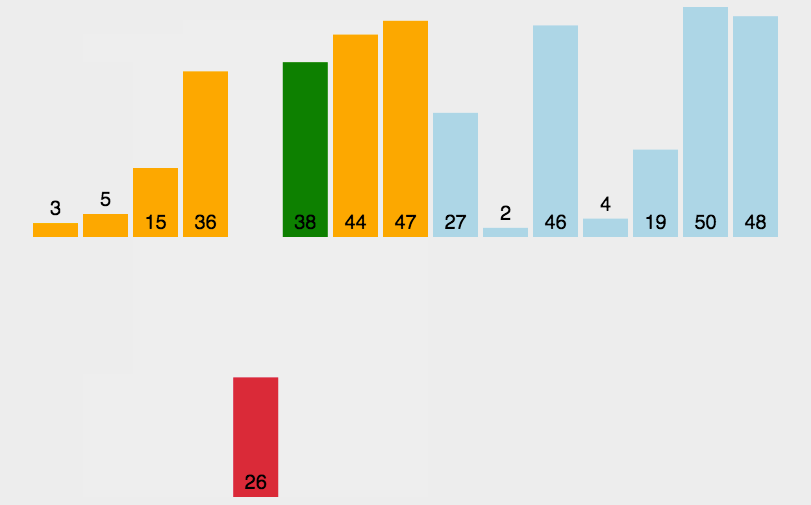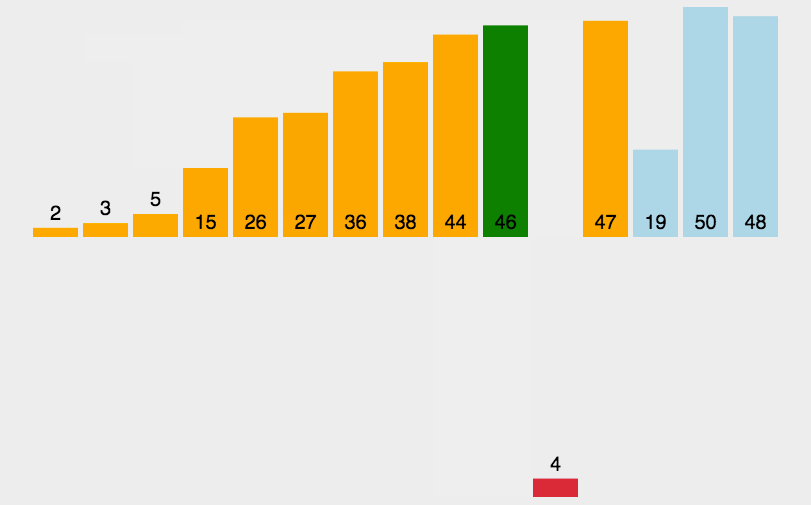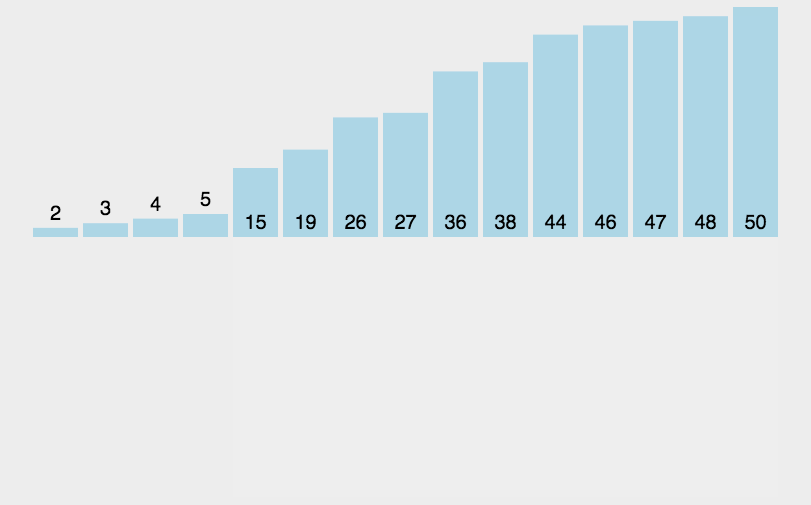
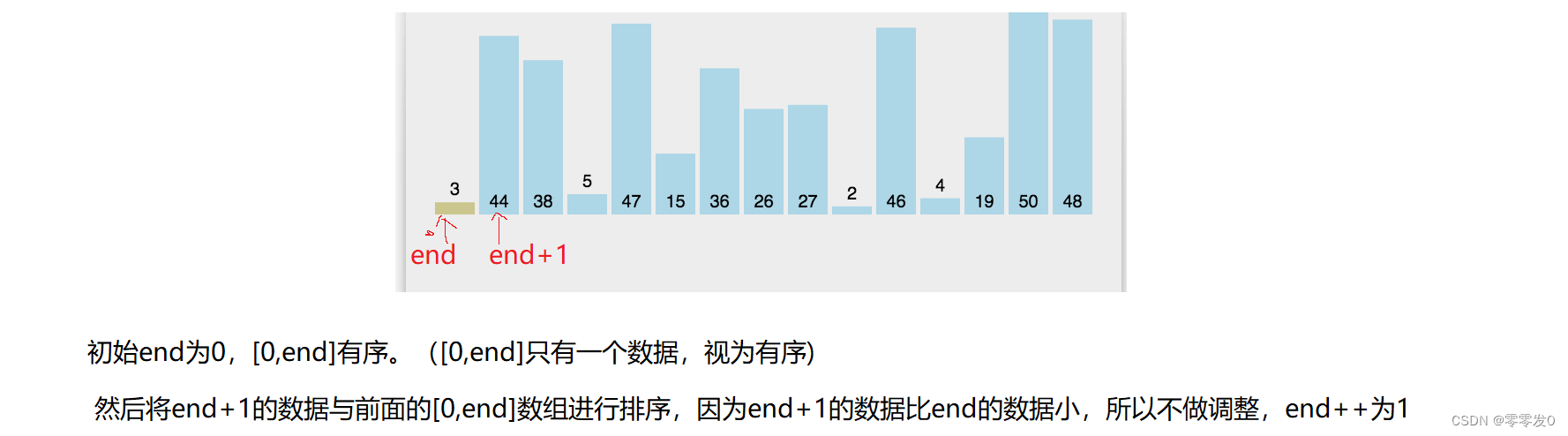
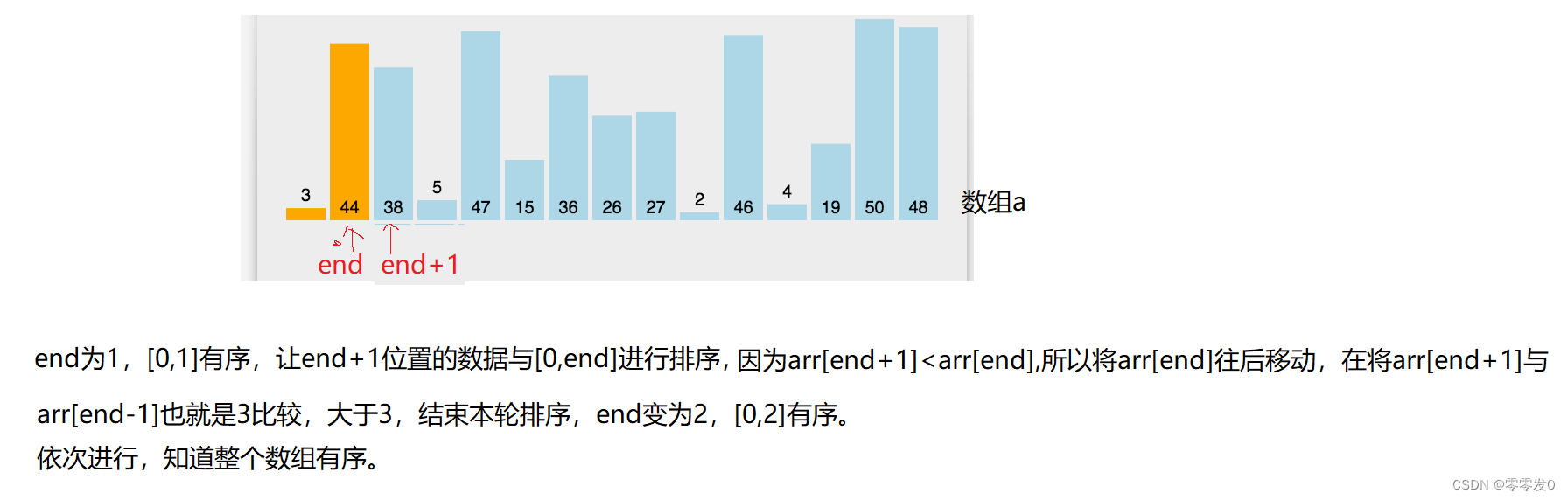
基本思想:
end从0开始,[0,end]视为一个有序的数组,然后每次都让end+1的数据与前面有序数组[0,end]进行对比排序,然后end++,直至遍历完整个数组,此时原数组就有序了。
代码
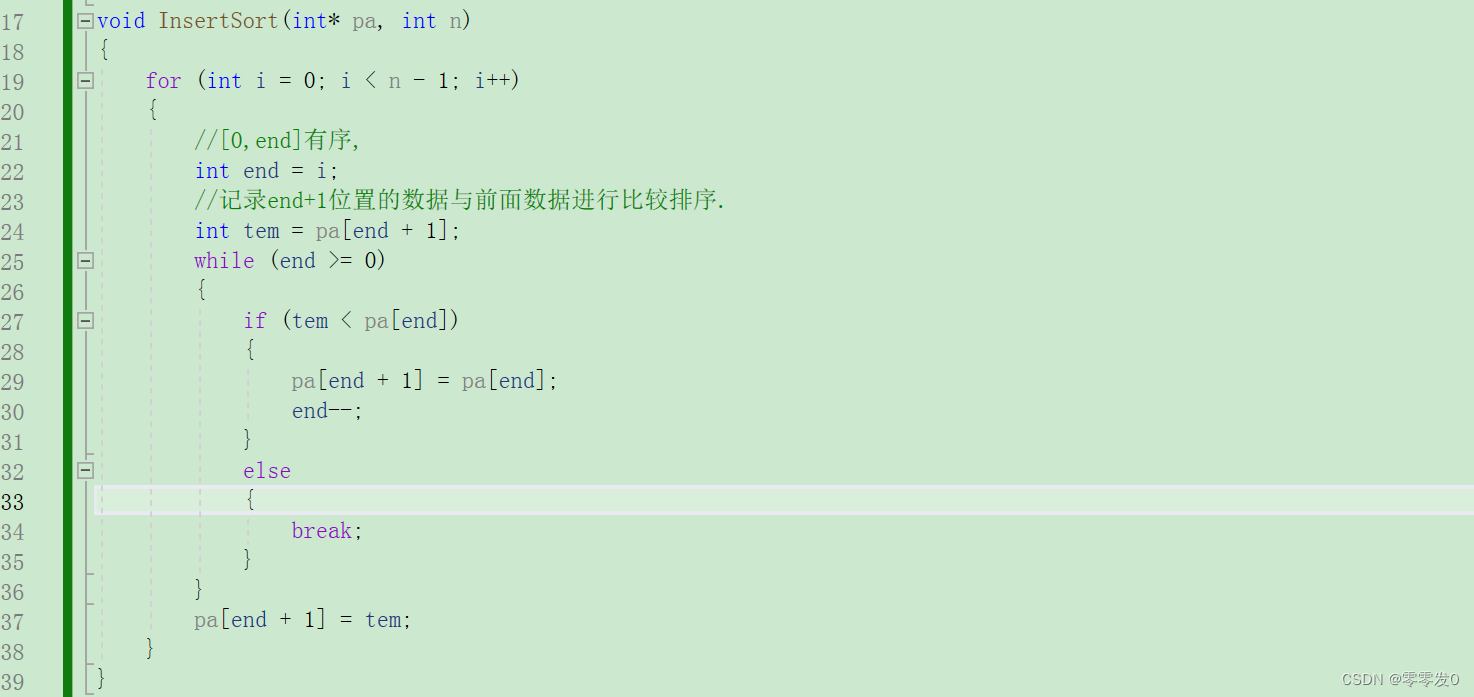
有小伙伴可能会问,为什么最后要pa[end+1]=tem ?且看此图:

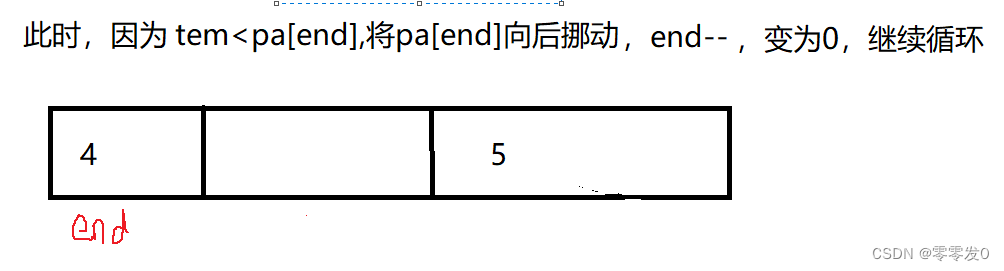
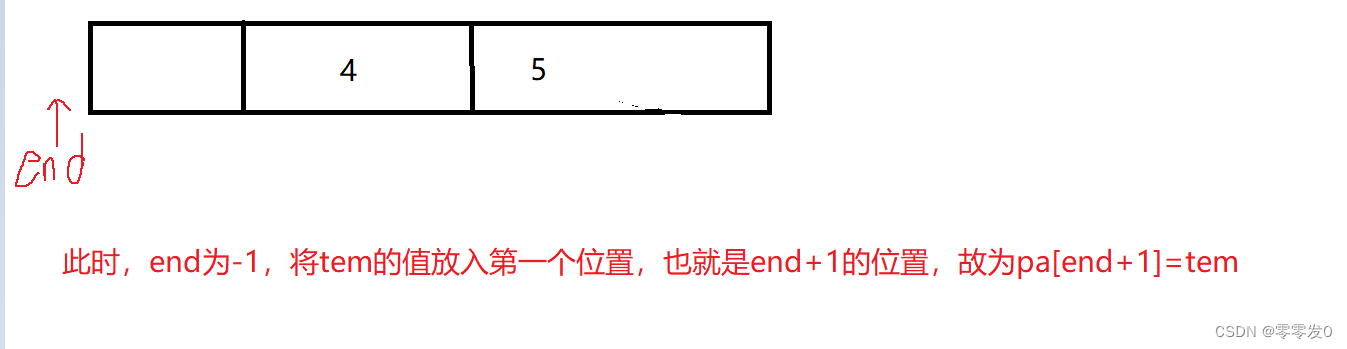
这就是上面问题的原因,其实学习数据结构时,有这种问题究其原因还是因为没有画图,笔者认为学习数据结构一定要多画图,这样才不容易出错,有点跑题了哈哈,我们继续学习下一个排序。
希尔排序:
首先,希尔排序其实就是直接插入排序的变形,所以要理解希尔排序,我们得熟练掌握直接插入排序。我们先来看一下动图:
是不是看的一脸懵?这就对了,这个思路还是有点抽象的,容笔者慢慢讲解:
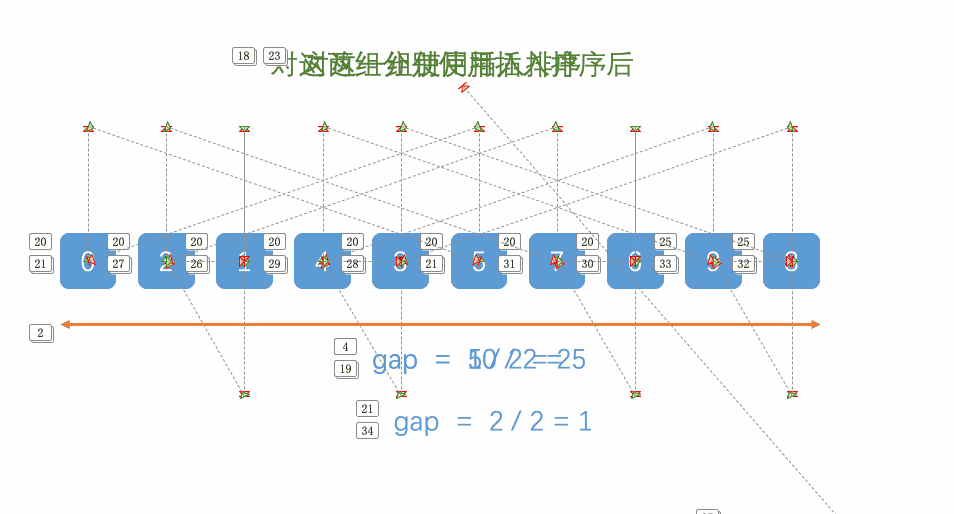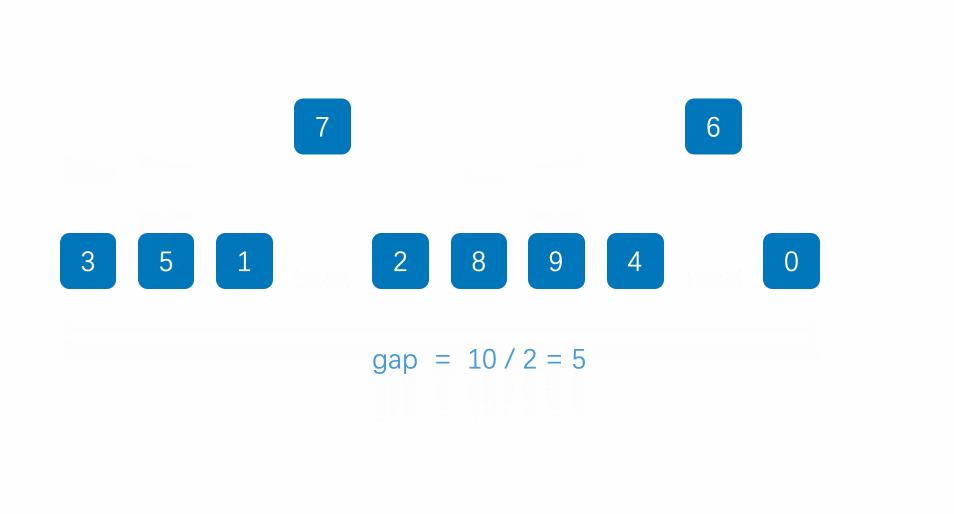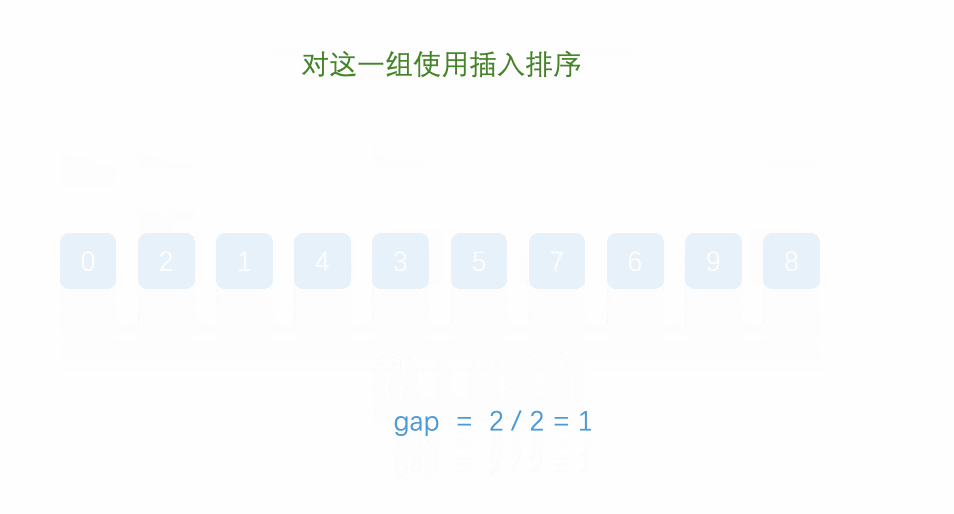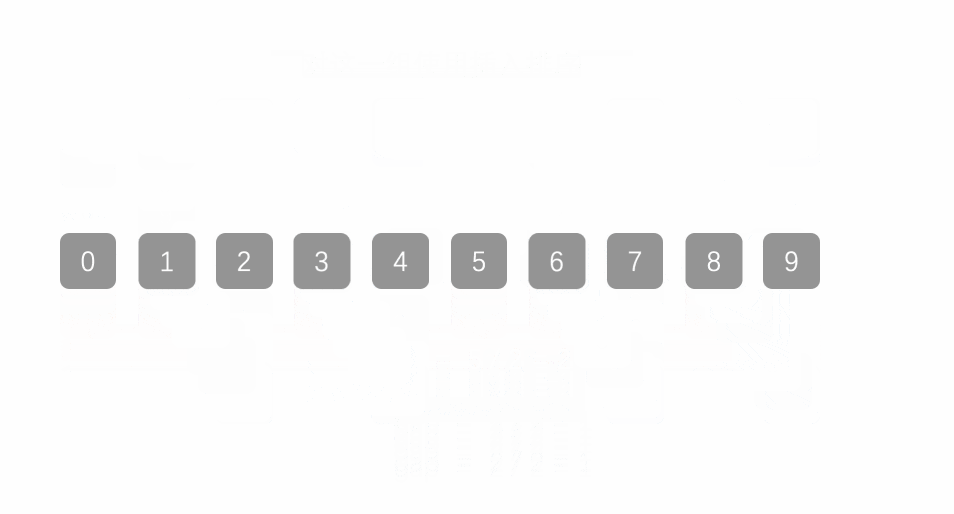
首先,我们要知道希尔排序其实就是直接插入排序的优化,它选取了一个值gap,并把数组分成gap个组,每个组两个元素相隔gap个位置,如下图所示:
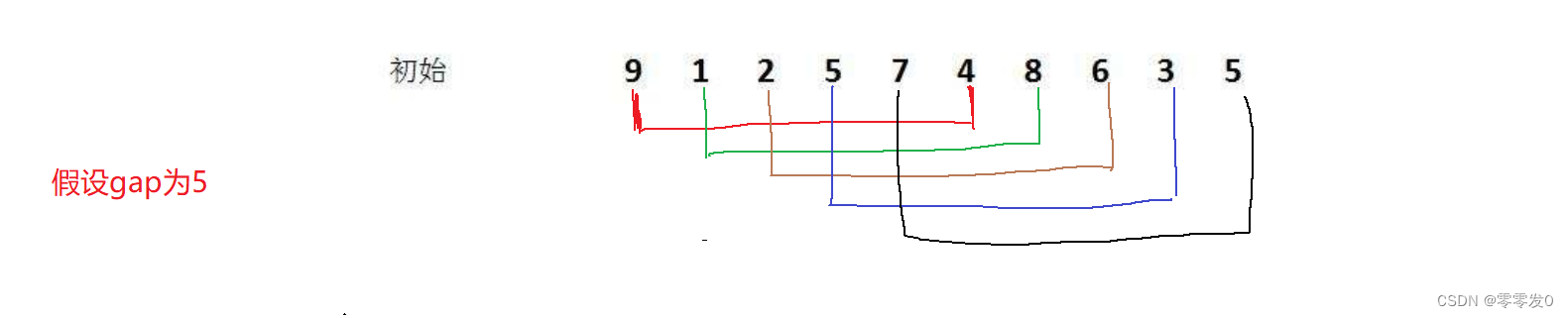
至于gap如何取值,我们一会儿再讲,如上图,我们讲数组分成了gap组(5组),每组两两元素之间相隔gap个位置。
**然后,我们对每一组进行直接插入排序,**结果如下:

然后gap=gap/2,此时gap为2,在把数组分成gap(2)组,每组相邻元素相差gap位置,如下:

在对每组进行直接插入排序,排好后如下:

然后gap为1,将数组分成了1组,有10个元素,对改组进行直接插入排序:

自此,数组有序。
有小伙伴可能发现了,当gap为1时不就是直接插入排序吗?没错所以会说希尔排序就是插入排序的变形,实际上希尔排序就是插入排序的优化,希尔排序可比插入排序快多了。关于各排序的时间复杂度,我们下篇文章在讲解。
gap取值
gap取值的话
一般取法有多种,其中两种常见的是:
-
取 n/2:
- 最初的增量(gap)设定为数组长度的一半,即
gap = n / 2。 - 然后每次将 gap 减半,直到 gap = 1。
- 最初的增量(gap)设定为数组长度的一半,即
-
取 n/3+1:
- 初始增量(gap)设定为
gap = n / 3 + 1。 - 然后每次将 gap 按一定规则缩小,直到 gap = 1。
- 初始增量(gap)设定为
上面我们就是用了第一种方法。
当gap>1时,被称作为预排序;当ga1p=1为插入排序。
代码
代码如下:

果然,当我们了解思路后写代码,发现还是一样难写,哈哈哈。

第一个for循环,是控制所有组,确保每一组都能进行排序,一共有gap组,故为i<gap.

而这段代码,就是控制一组的排序,这个过程其实就是插入排序的变形,当gap=1时,与插入排序一模一样,我们可以画图来进行理解。
需要注意的是j<n-gap:

因为我们进行排序时,有pa[end+gap]=pa[end],所以我们要让j<n-gap,防止越界。
希尔排序还有另外一种写法:
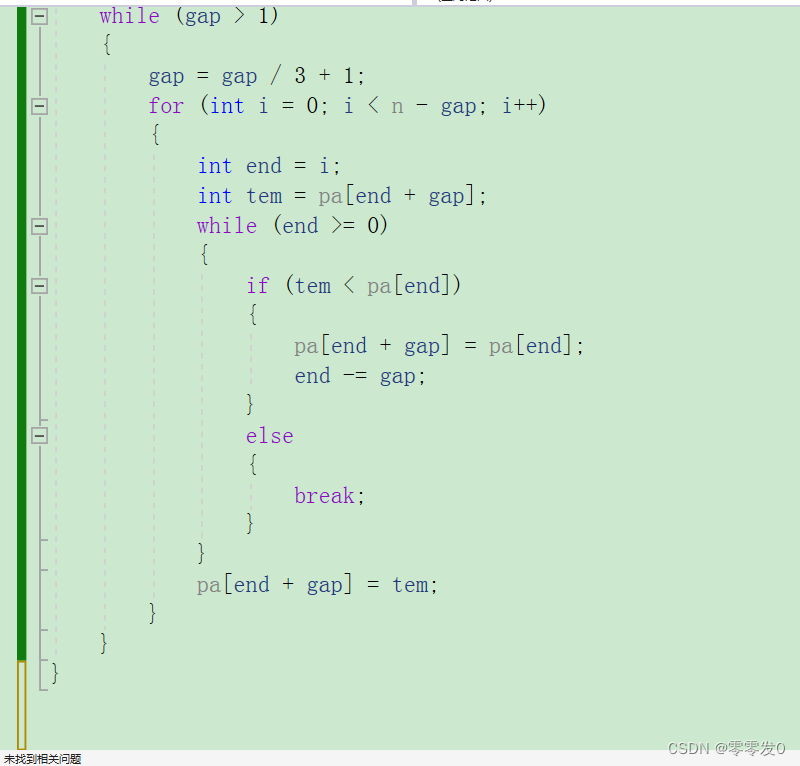
这个写法与第一个不同的是没有按照先排好一个组,然后再排另一个组,它直接是混着排序,小伙伴们可以画图理解一下。两种方法掌握一种即可。
特性总结

选择排序
基本思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的 数据元素排完 。
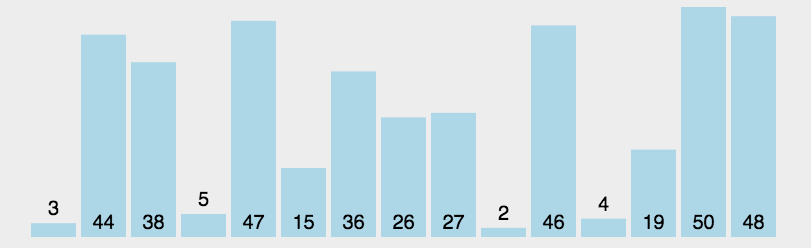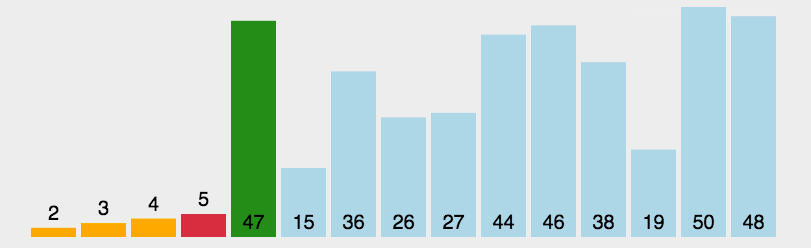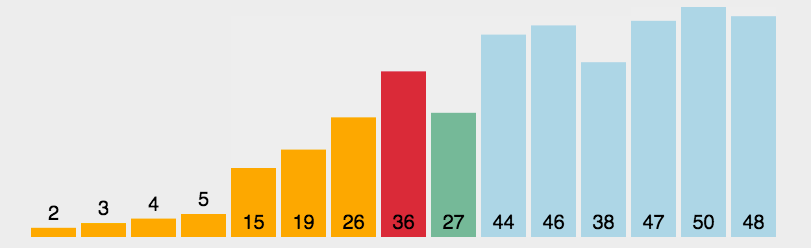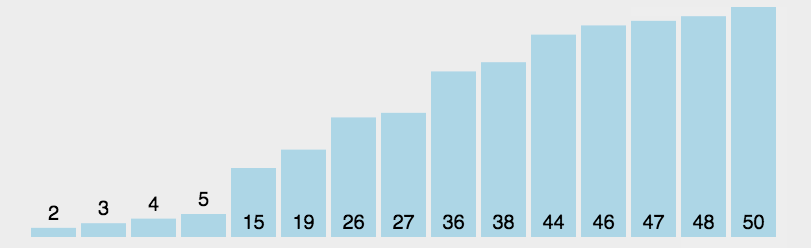
这个排序思路还是比较简单的,
代码
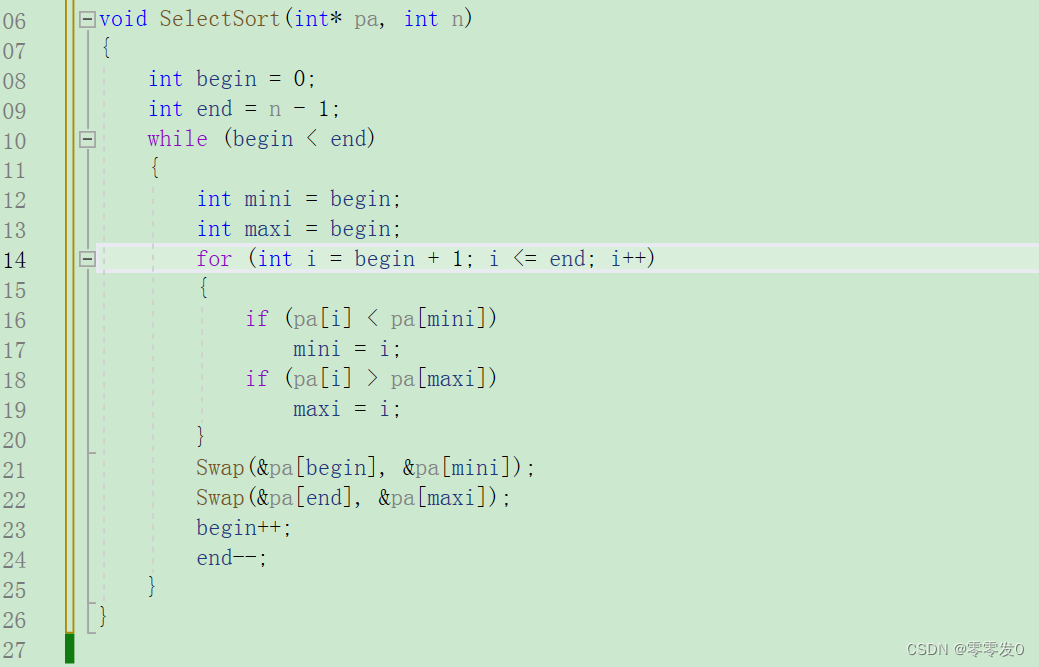
好,我们给个样例运行一下:
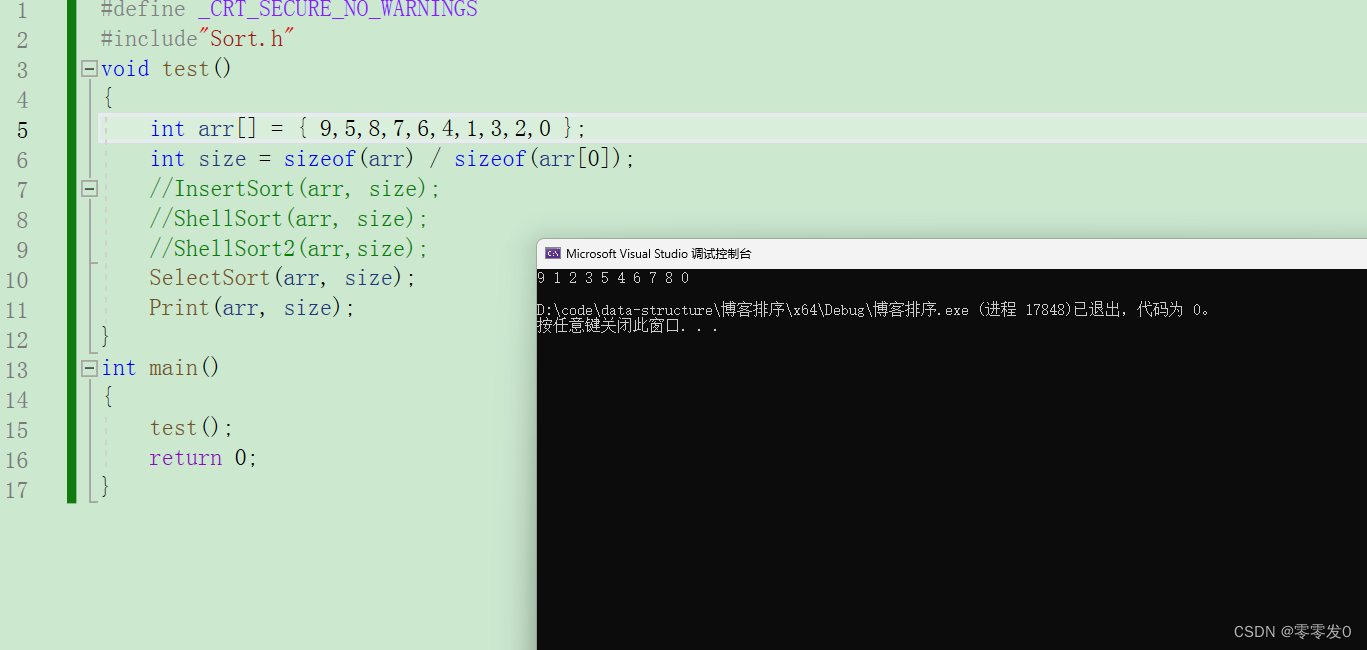
不出意外,错了!
为啥呢?我们来调试一下:
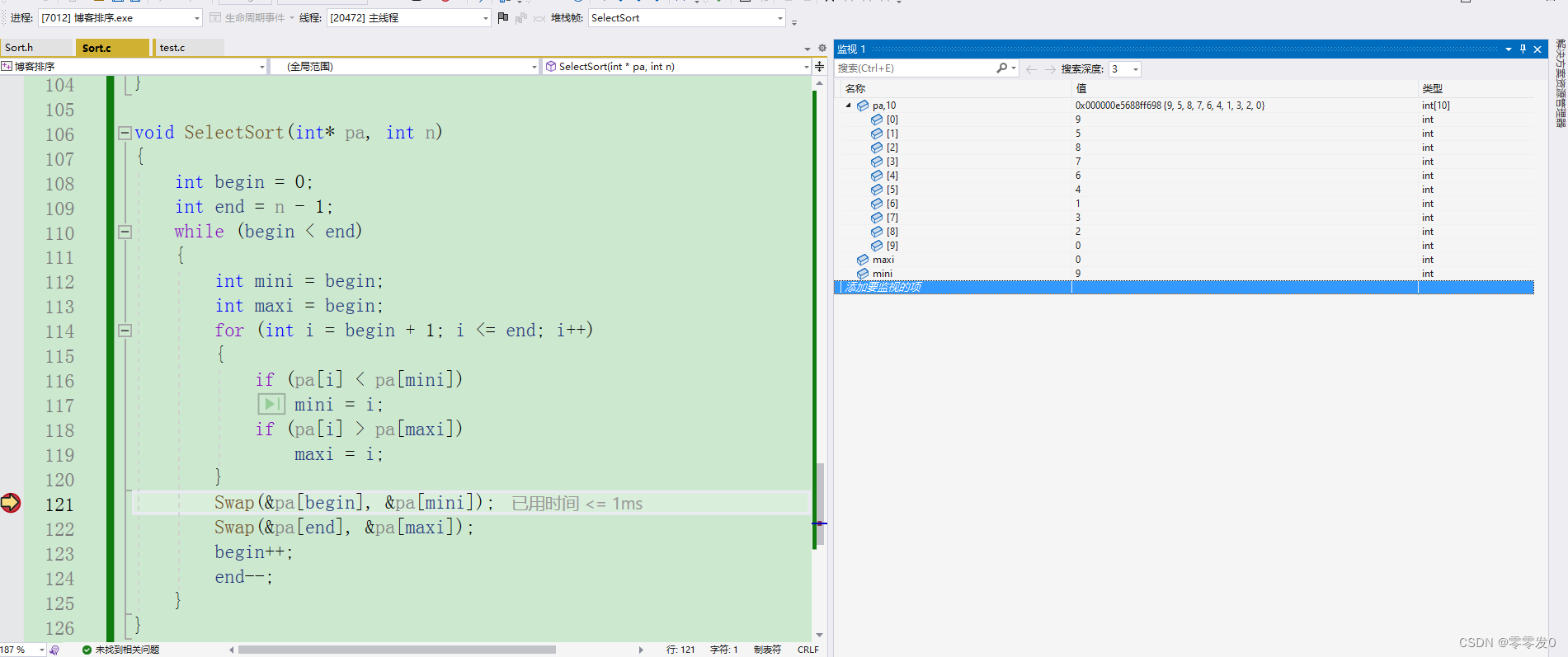
第一轮,maxi为0,mini为9,没有错,我们在进行下面的交换代码。
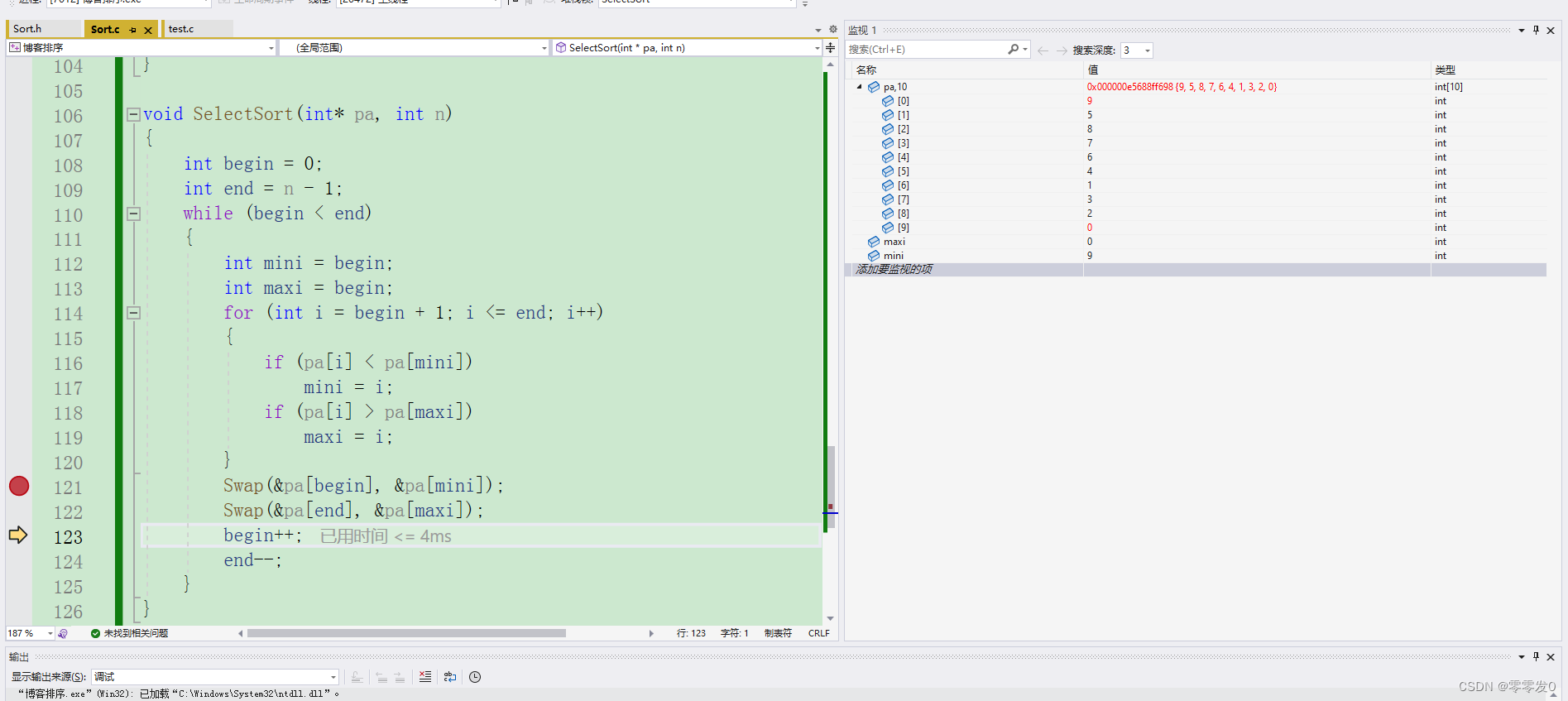
出问题了,当我们把pa[begin]和pa[mini]进行交换时,由于maxi的值与begin相等,所以当交换pa[begin]和pa[mini]后,maxi指向的值就变了,不是最大值了,所以我们要加一个if条件语句:
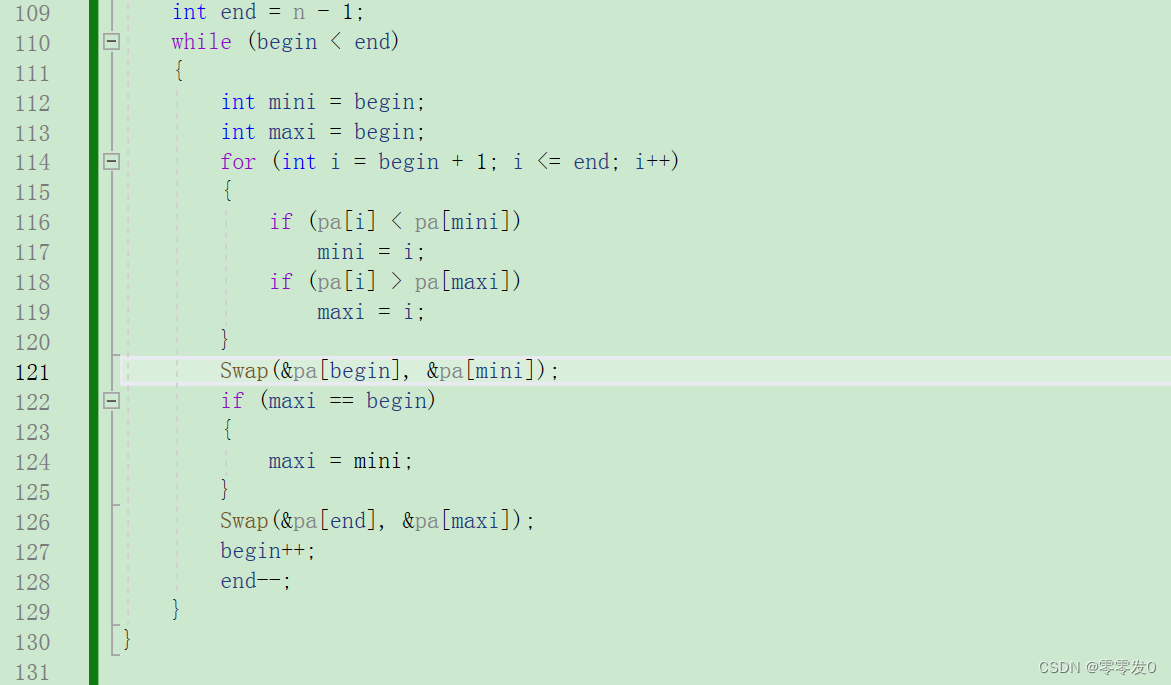
这下就对了。
堆排序
思想
首先建堆,升序建大堆,降序建小堆,建好堆之后另end等于数组长度-1,交换0位置和end位置的数据,向下调整建堆end--,直至end小于0。
 、
、
代码
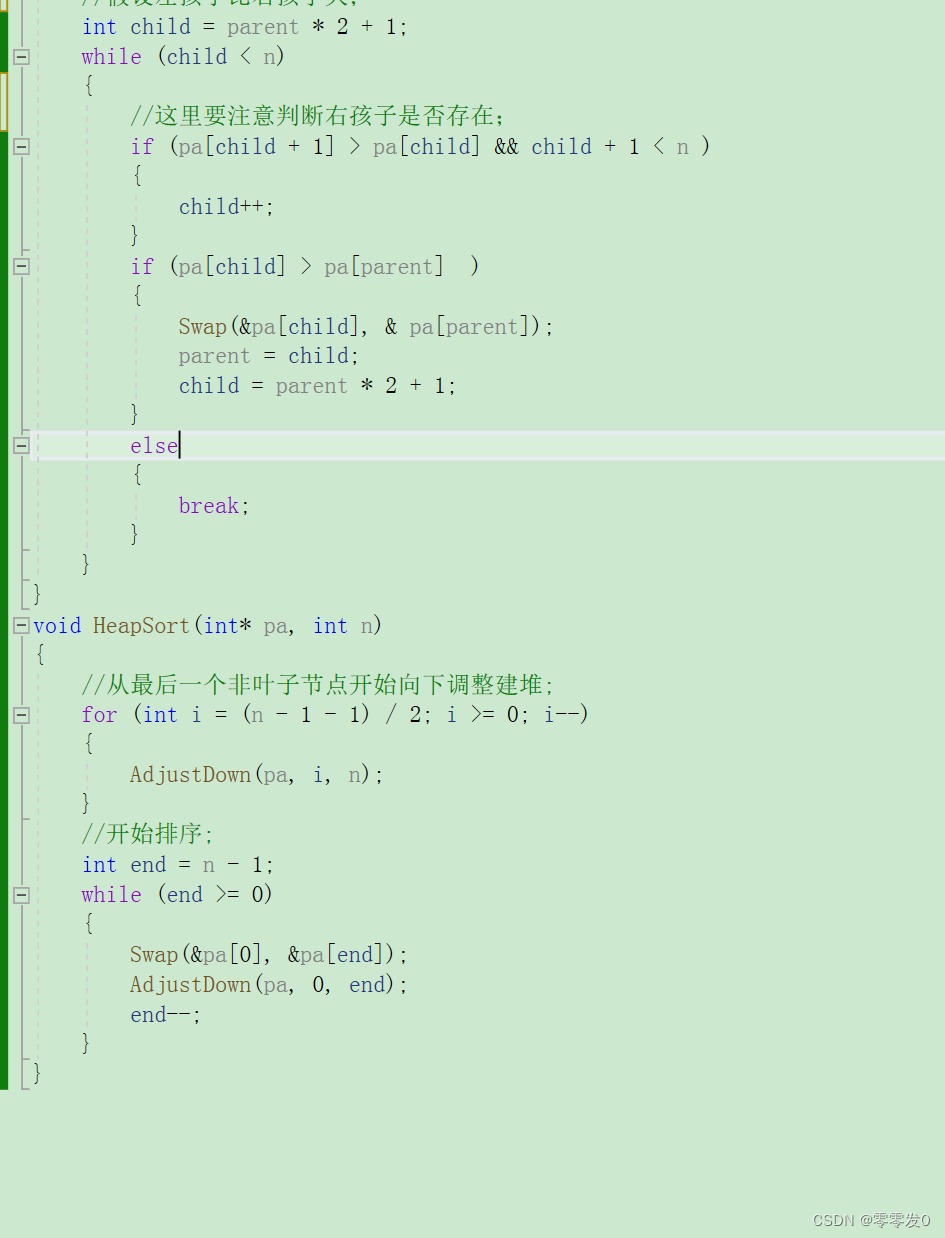
这个堆排序写起来还是有难度的,这里看不懂也没关系,笔者之后专门写一篇堆排序的文章,可以暂时跳过继续往下看。
冒泡排序:
这个就比较简单了,冒泡排序没有什么实践价值,但有一定的教学意义,我们来看一下动图: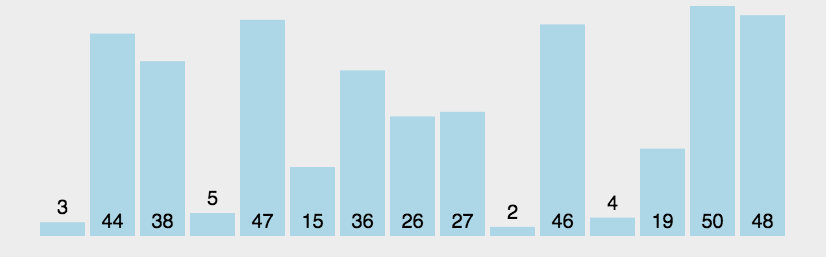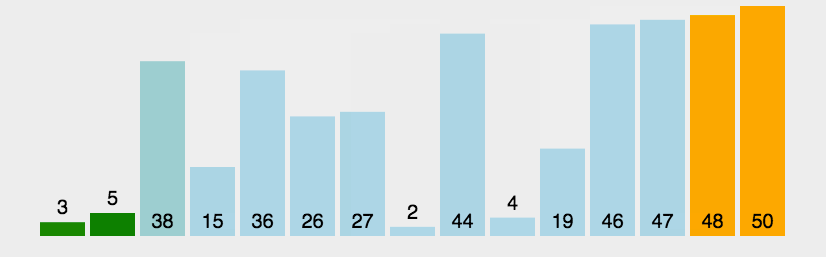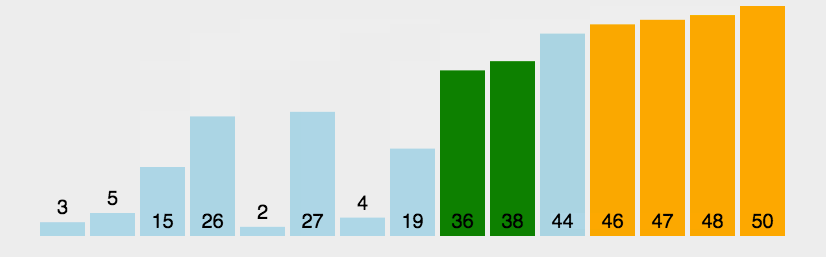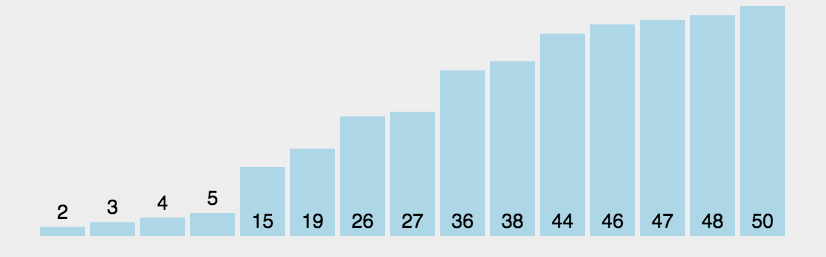
代码如下:

快速排序:
思想
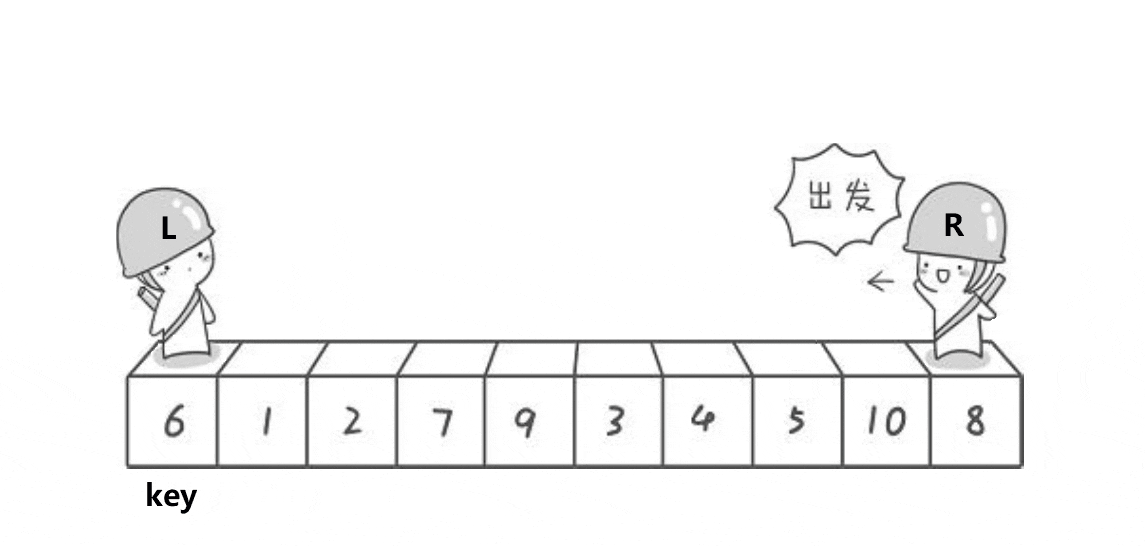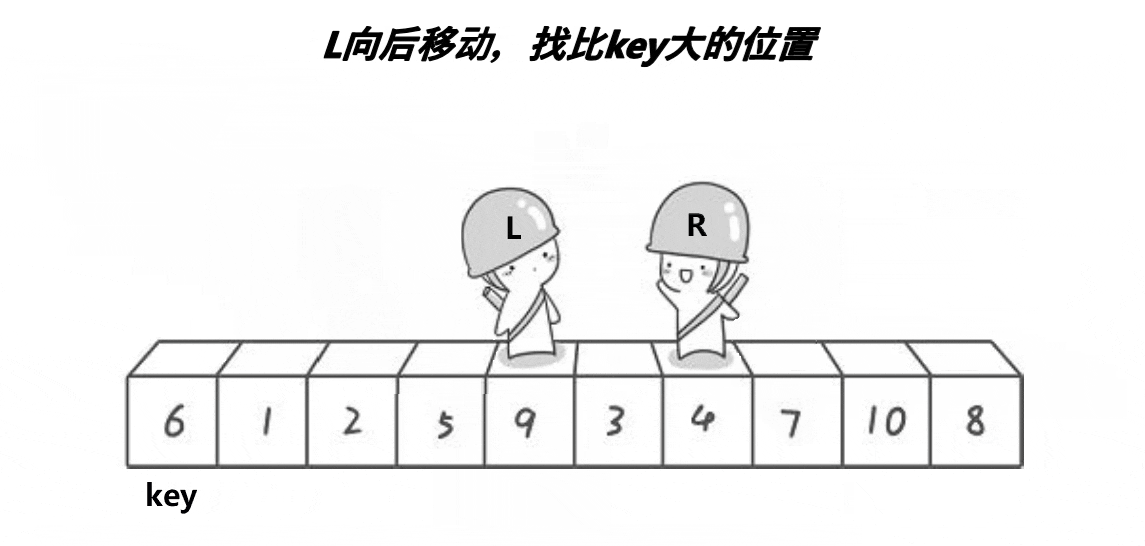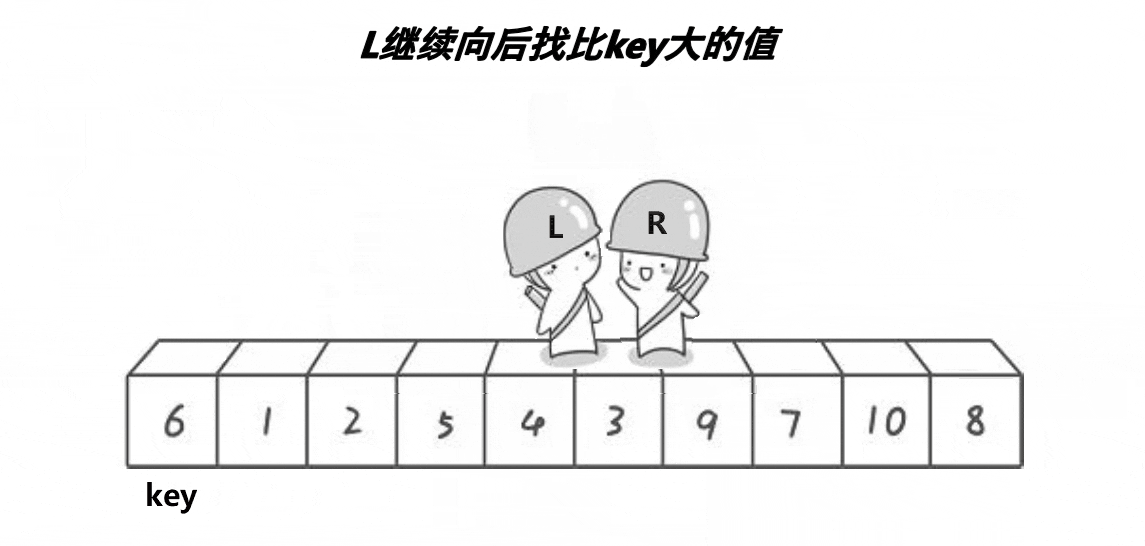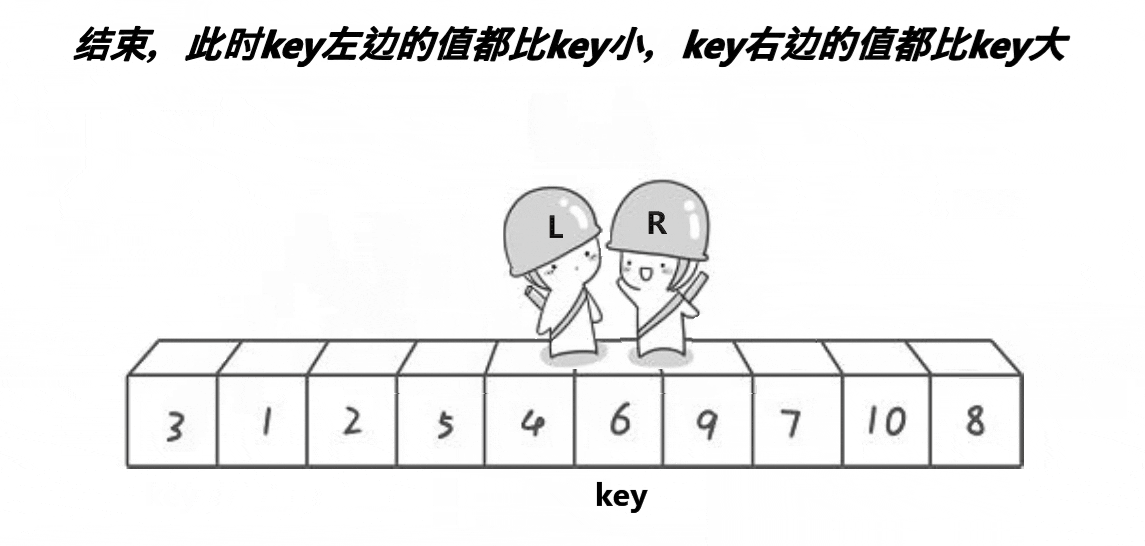
我们找一个参考值,end指向数组尾部,begin指向数组起始位置。
end先走,如果arr[end]大于key,end--直至找到小于key的位置;
同理,当end找到小于key的位置后,begin开始找大于key的位置,然后交换begin和end两位置的值,直至begin=end。
当begin和end相遇时的位置的值一定小于key。(原因我们一会儿讲),然后交换key和两者相遇位置的值,完成第一趟排序。
快排是比较重要的,还是有很大的概率在面试时让你手撕,所以我们一定要熟练掌握,快排实现有递归和非递归两种方法,我们一一讲解。
递归
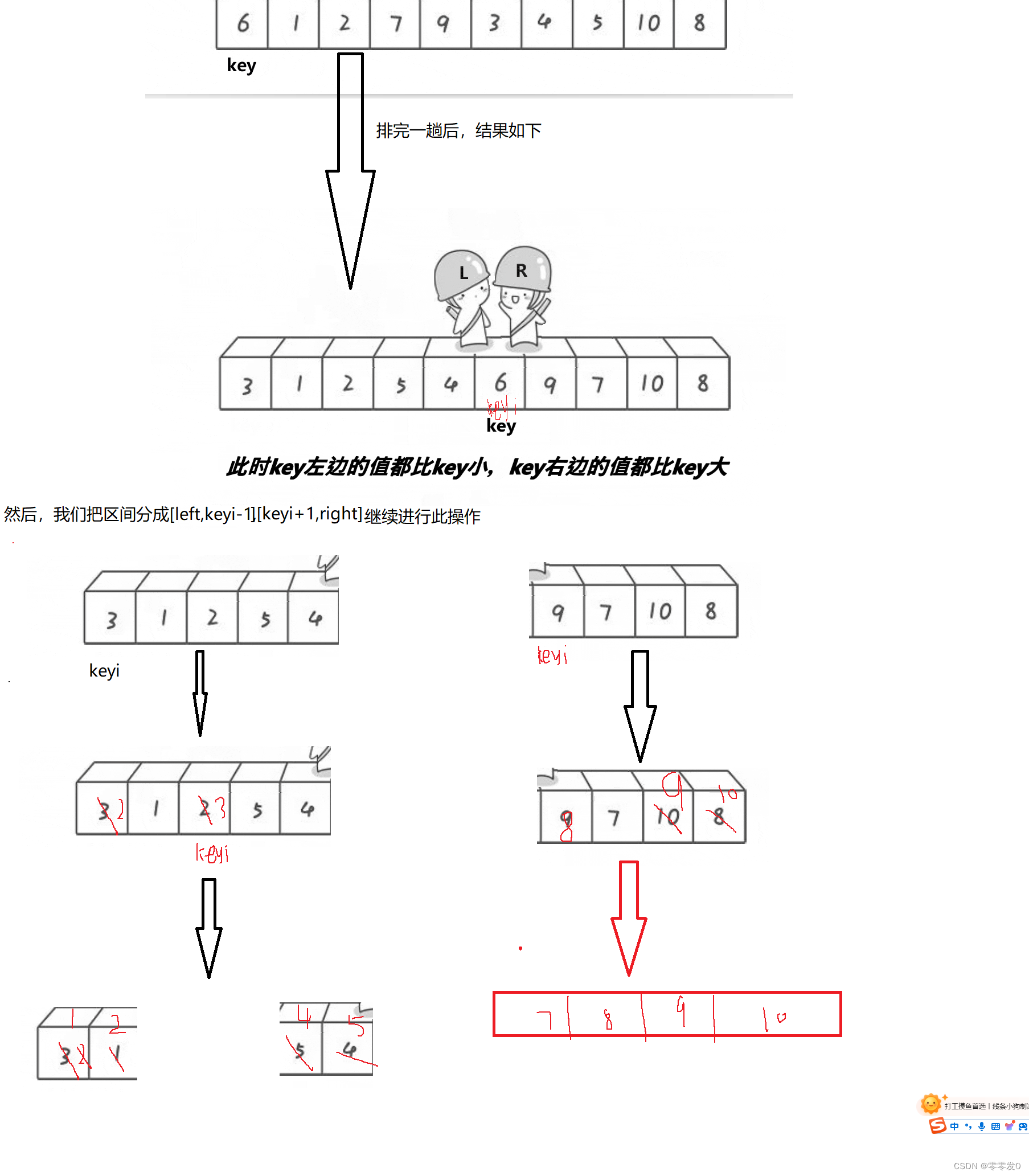
排完一次序后,以keyi为基准分割区间,继续排序.
代码如下:
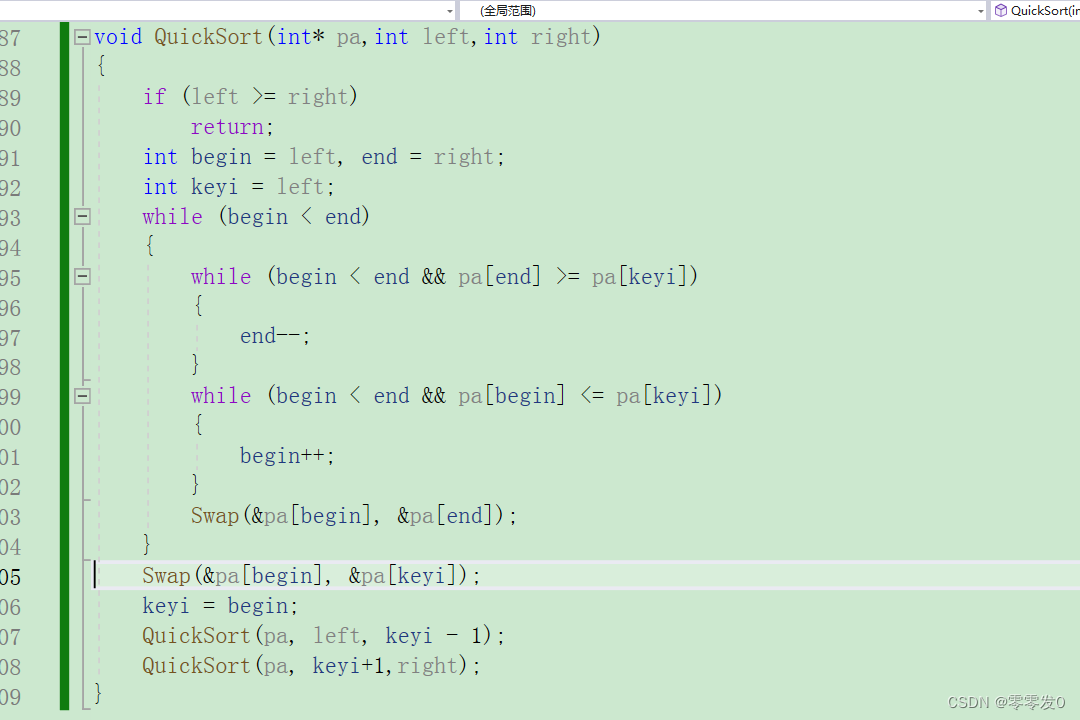
非递归
有小伙伴可能会说:我们都已经会递归版本的快排了,还有必要学这个吗?往年一个面试官是这样问的:同学,你学过数据结构,那你了解快排吗?这位同学非常熟练的讲出来了递归实现的大致思路。面试官听后笑着说:"很好,那你能用非递归实现吗?"哈哈哈,所以还是有必要的。
非递归和递归思路一样,我们也是采用分割区间,不能用递归,我们可以用循环来解决,那么问题来了,我们怎么来存储分割好的区间呢?
想想我们之前讲过一道括号匹配的问题,那个时候我们怎么存储括号的?
答案是:栈。
我们用栈来存储分割后的区间,只要区间满足左边界大于右边界就入栈,然后套一个while循环,当战不为空就继续。
需要注意的是栈是后进先出,千万不要把区间搞反了
代码如下:

归并排序
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
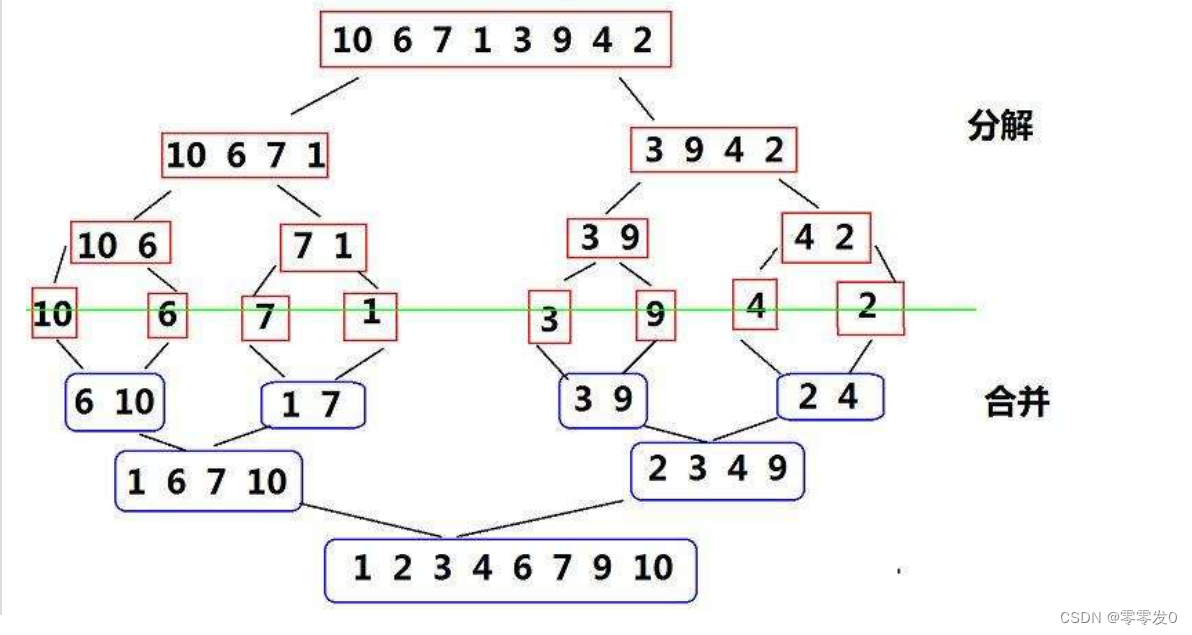
说的通俗易懂点就是把一个数组分解成两个数组pa1,pa2,直到每个数组只有一个元素,然后在依次合并pa1和pa2,从而使原数组有序。
归并排序的思想很像我们之前讲过的合并两个有序数组,不知道小伙伴还记不记得,只能说是一模一样,同样,实现归并排序也有递归和非递归两种方式。
递归实现

需要讲的一点是_MergeSort是MergeSort的子函数,也可以稍作修改,写在一起.还有就是记得释放动态开辟的内存,养成良好的代码风格。
下面是递归大致展开图,可以帮助大家理解一下:
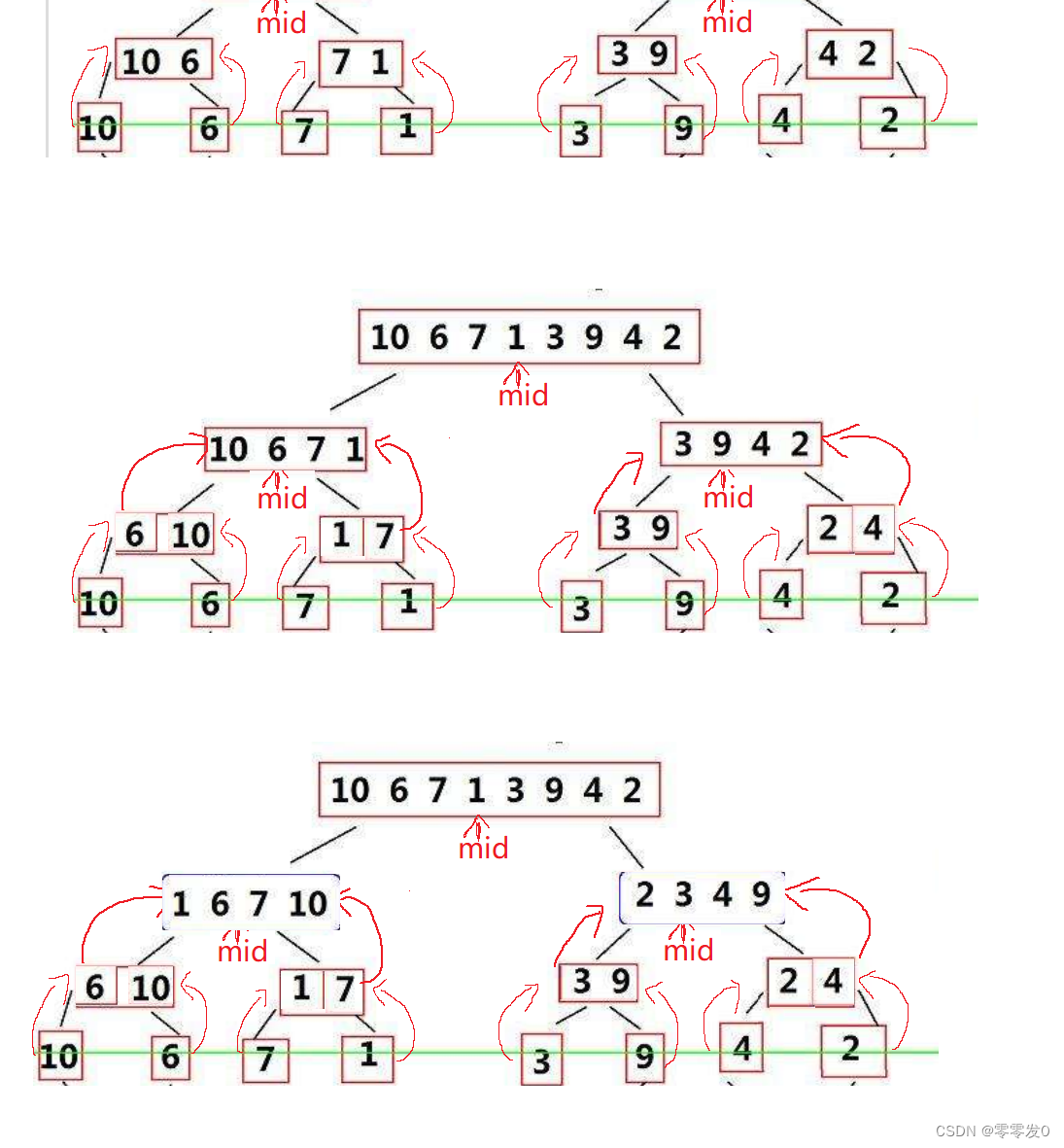
非递归实现
非递归实现,怎么实现呢?我们上面快排的非递归实现运用了栈来解决,那么这里能用栈来解决问题吗?可以,但是这里就比较麻烦,如果我们用栈来解决的话,那么循环的结束条件难以判断,同时此处栈管理起来也比较麻烦。我们这里可以用迭代来实现。

需要注意的是,我们每次要归并的两组数据,end1,begin2,end2有可能会越界,因为for循环的判断条件是i<n-1,此时除了begin1其余三个都可能会越界,所以我们要判断修正。
**当begin2越界时,代表第二组越界,也就是不存在,所以不需要归并;当只有end2越界时,只需把end2修正为最后一个元素继续归并即可。**其余也就没什么好说的了。
时间复杂度与空间复杂度以及稳定性
首先,我们先来了解一下稳定性的概念:
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。

如上图所示,即排完序后,黑6与红6的相对位置不变(黑6还在红6前面),那么这个排序就是稳定的。
知道了这个,我们接下来一个一个分析上面各个排序算法的时间复杂度、空间复杂度以及稳定性
1.直接插入排序
稳定性:稳定
时间复杂度:O(N^2);
空间复杂度:O(1)。
直接插入排序[0,end]有序,让arr[end+1]与[0,end]进行比较交换,当两数相等时,我们可以让其不交换,那么最后拍完序相等元素的相对顺序是不变的,所以说直接插入排序是稳定的。
通过上面的代码,不难分析出直接插入排序的时间复杂度为O(n^2),由于没开辟新的空间,所以说空间复杂度为O(1)。
2.希尔排序
稳定性:不稳定
时间复杂度:O(N*logN)
空间复杂度:O(1)
我们上面讲,希尔排序是插入排序的变形,那么希尔排序稳定吗?答案是不稳定。
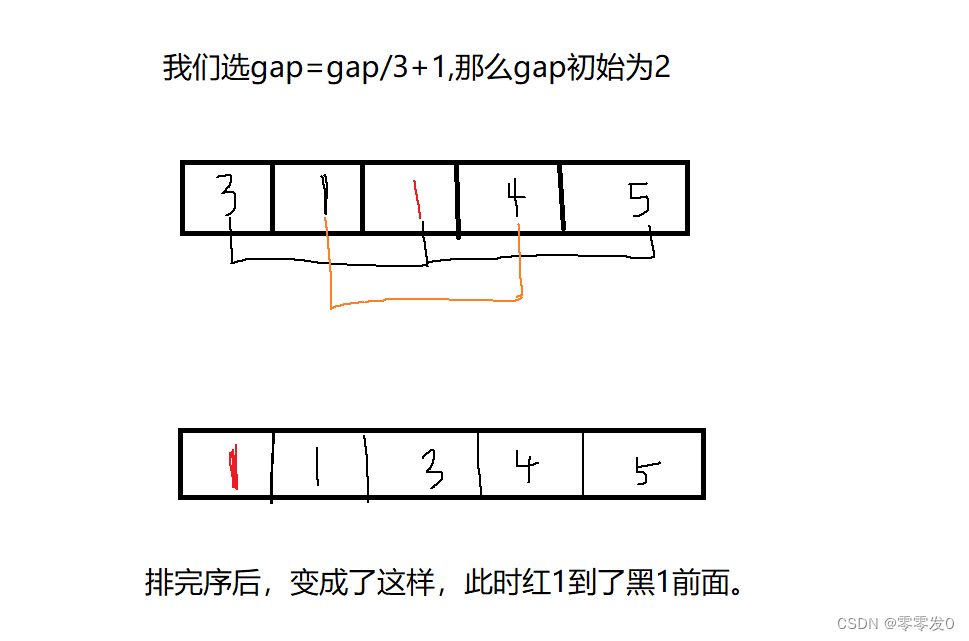
故希尔排序不稳定。那么希尔排序的时间复杂度又为多少呢?
这个就很复杂了,因为希尔排序循环次数与gap的取值有关,而gap又有很多种不同的取值方法,

同时,while循环比较次数和元素移动的次数也难以计算,所以说这需要很强的数学专业知识,笔者不会,但有大佬给出希尔排序的时间复杂度大概为O(N^1.3),记住就行。
那么希尔排序的空间复杂度为多少呢?很显然是O(1)。
3.选择排序
稳定性:不稳定。
时间复杂度:O(N^2);
空间复杂度:O(1)。
选择排序为什么不稳定的,这是个易错点,我们看下图的分析:

这种情况就是不稳定的情况。时间复杂度空间复杂度比较简单,不再赘述.
4.堆排序
稳定性:不稳定。
时间复杂度:O(n*logN)
空间复杂度:O(1)
由于堆我们之前没有讲解,讲起来有一点麻烦,我们先放一下,之后专门讲解堆的相关知识。
5.冒泡排序
稳定性:稳定
时间复杂度:O(N^2);
空间复杂度:O(1);
6.快速排序
稳定性:不稳定。
时间复杂度:O(N*logN);
空间复杂度:O( logn)~O(n)。
快排也无法保证相等元素的相对位置,这个很好想例子,比如下图**:**
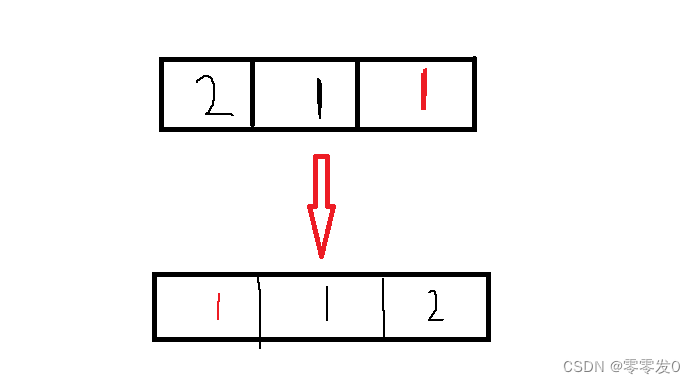
这里的易错点就是空间复杂度不是O(1)!!!
函数递归需要额外开辟空间,我们上面也讲了,快排通常是递归实现的,N个数组成的数组每次被分成两个区间,依次分割,直到left>=right,它一共分了logN次,故需要开辟logN个新的空间
有小伙伴会问,递归递归,它往回归的时候,不是又应该开辟一块新空间吗?好问题,函数递归,回归时用的是已经开辟好了的空间。这涉及到函数栈帧的问题,有兴趣的小伙伴可以去学习学习,增强内力。
7.归并排序
稳定性:稳定
时间复杂度:O(N*logN).
空间复杂度:O(N).
也没什么好说的,比较简单。
总结图: 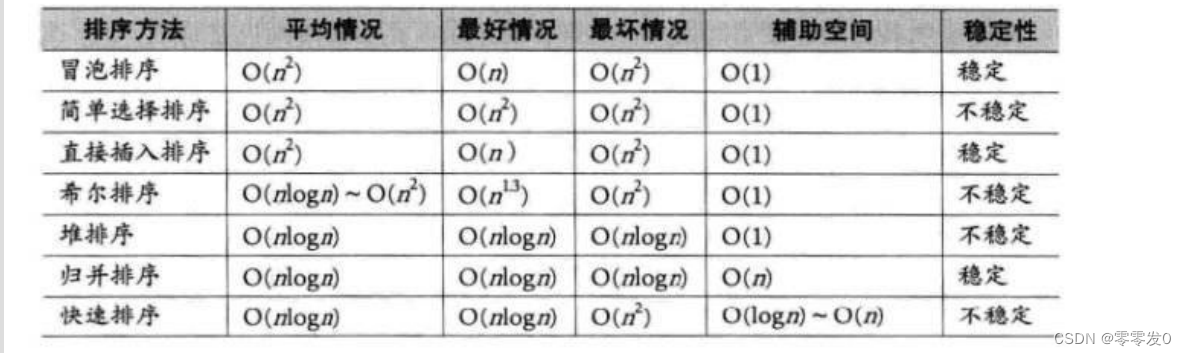
笔者希望大家能够理解性的去记忆这些东西,理解它们的原理,这样记忆起来就事半功倍了。