[深度学习] 卷积神经网络CNN

藓类少女2024-06-30 2:05

卷积神经网络（Convolutional Neural Network, CNN）是一种专门用于处理数据具有类似网格结构的神经网络，最常用于图像数据处理。

一、CNN的详细过程：

1. 输入层

输入层接收原始数据，例如一张图像，它可以被表示为一个三维矩阵（高度、宽度和颜色通道）。

2. 卷积层（Convolutional Layer）

卷积层是CNN的核心组件之一，通过卷积操作提取输入数据中的特征。卷积层的步骤如下：

  • 卷积操作：使用若干个滤波器（也称为卷积核）在输入数据上进行滑动窗口操作。每个滤波器是一个较小的矩阵，它在输入数据的各个位置上进行矩阵乘法和加和运算，生成一个特征图。
  • 激活函数：通常在卷积操作后应用激活函数（如ReLU）引入非线性，使模型能够学习更复杂的特征。

3. 池化层（Pooling Layer）

池化层用于减少特征图的尺寸，从而减少参数和计算量，同时控制过拟合。常见的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。

  • 最大池化：取池化窗口中的最大值。
  • 平均池化：取池化窗口中的平均值。

4. 归一化层（Normalization Layer）

有时在卷积层和池化层之间会插入归一化层（如批量归一化），以加速训练过程并稳定模型性能。

5. 全连接层（Fully Connected Layer）

在经过若干个卷积和池化层后，通常会将特征图展平（flatten）为一个向量，然后输入全连接层。这类似于传统的神经网络，每个节点与前一层的所有节点相连。

6. 输出层

输出层通常是一个全连接层，用于生成最终的分类结果或其他任务的结果。

7. 损失函数（Loss Function）和优化（Optimization）

  • 损失函数：用于评估模型预测与实际标签的差距，如交叉熵损失（Cross-Entropy Loss）用于分类问题。
  • 优化算法：常用的优化算法有随机梯度下降（SGD）及其变种（如Adam），用于调整模型参数以最小化损失函数。

8. 训练过程

  • 前向传播（Forward Propagation）：将输入数据依次通过各层，计算输出。
  • 反向传播（Backward Propagation）：通过链式法则计算损失函数相对于每个参数的梯度，并更新参数。

9. 迭代训练

模型通过多次迭代训练，不断调整参数，使损失函数值逐渐减小，模型性能逐渐提升。

10. 评估和测试

使用独立的验证集和测试集评估模型性能，确保模型对新数据有良好的泛化能力。

卷积神经网络通过卷积层提取特征，池化层降维，全连接层进行分类，损失函数和优化算法进行参数调整，逐步提升模型性能，最终实现对图像等数据的有效处理和分析。

二、cnn模型构建过程举例

假设输入形状为 (5, 5, 1)，并使用一个3x3的卷积核，stride为1，padding为same。

Stride是卷积核在输入图像上移动的步长。Stride定义了卷积核每次移动的像素数。常见的stride值有：

stride=1：卷积核每次移动一个像素。产生的特征图尺寸较大。
stride=2：卷积核每次移动两个像素。产生的特征图尺寸较小，计算量也较少。

Padding是在输入图像的边缘添加额外的像素，以保持输出特征图的尺寸。常见的padding类型有：

valid（无填充）：不进行填充，卷积核只在输入图像内部滑动。特征图尺寸会缩小。
same（相同填充）：进行填充，使得卷积后输出特征图的尺寸与输入图像相同。通常在每一边添加适当数量的零填充。

1. 输入层

假设输入图像为5x5的灰度图，像素值如下：

[
 [0, 1, 2, 1, 0],
 [1, 2, 3, 2, 1],
 [2, 3, 4, 3, 2],
 [1, 2, 3, 2, 1],
 [0, 1, 2, 1, 0]
]

2. 第一个卷积层

使用一个3x3卷积核，stride为1，padding为same。假设卷积核如下：

[
 [1, 0, -1],
 [1, 0, -1],
 [1, 0, -1]
]

先进行填充操作：

填充后的输入图像（周围填充一圈0）：

[
 [0, 0, 0, 0, 0, 0, 0],
 [0, 0, 1, 2, 1, 0, 0],
 [0, 1, 2, 3, 2, 1, 0],
 [0, 2, 3, 4, 3, 2, 0],
 [0, 1, 2, 3, 2, 1, 0],
 [0, 0, 1, 2, 1, 0, 0],
 [0, 0, 0, 0, 0, 0, 0]
]

卷积操作步骤如下：

你是对的，如果使用 padding='same'，在进行卷积操作之前，我们应该先对输入图像进行填充。下面我将详细说明每一步的计算过程，包括填充步骤。

1. 输入层

假设输入图像为5x5的灰度图，像素值如下：

[
 [0, 1, 2, 1, 0],
 [1, 2, 3, 2, 1],
 [2, 3, 4, 3, 2],
 [1, 2, 3, 2, 1],
 [0, 1, 2, 1, 0]
]

2. 填充

在进行卷积操作之前，使用 padding='same'，我们需要在图像周围填充0，以保持输出图像尺寸与输入图像相同。填充后的图像为7x7：

[
 [0, 0, 0, 0, 0, 0, 0],
 [0, 0, 1, 2, 1, 0, 0],
 [0, 1, 2, 3, 2, 1, 0],
 [0, 2, 3, 4, 3, 2, 0],
 [0, 1, 2, 3, 2, 1, 0],
 [0, 0, 1, 2, 1, 0, 0],
 [0, 0, 0, 0, 0, 0, 0]
]

3. 第一个卷积层

使用一个3x3卷积核，stride为1，padding为same。假设垂直边缘检测卷积核如下：

[
 [1, 0, -1],
 [1, 0, -1],
 [1, 0, -1]
]
卷积操作计算

  1. 对位置(0, 0)的3x3区域进行卷积（左上角）：

    (0*1 + 0*0 + 0*(-1)) + (0*1 + 0*0 + 1*(-1)) + (0*1 + 1*0 + 2*(-1))
= 0 + 0 + 0 + 0 + 0 - 1 + 0 + 0 - 2
= -3

  2. 对位置(0, 1)的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (0*1 + 1*0 + 2*(-1)) + (0*1 + 2*0 + 3*(-1))
= 0 + 0 + 0 + 0 + 0 - 2 + 0 + 0 - 3
= -5

  3. 对位置(0, 2)的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (1*1 + 2*0 + 1*(-1)) + (2*1 + 3*0 + 2*(-1))
= 0 + 0 + 0 + 1 + 0 - 1 + 2 + 0 - 2
= 0

  4. 对位置(0, 3)的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (2*1 + 1*0 + 0*(-1)) + (3*1 + 2*0 + 1*(-1))
= 0 + 0 + 0 + 2 + 0 + 0 + 3 + 0 - 1
= 4

  5. 对位置(0, 4)的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (1*1 + 0*0 + 0*(-1)) + (2*1 + 1*0 + 0*(-1))
= 0 + 0 + 0 + 1 + 0 + 0 + 2 + 0 + 0
= 3

  6. 对位置(1, 0)的3x3区域进行卷积：

    (0*1 + 0*0 + 1*(-1)) + (0*1 + 1*0 + 2*(-1)) + (0*1 + 2*0 + 3*(-1))
= 0 + 0 - 1 + 0 + 0 - 2 + 0 + 0 - 3
= -6

  7. 对位置(1, 1)的3x3区域进行卷积：

    (0*1 + 1*0 + 2*(-1)) + (1*1 + 2*0 + 3*(-1)) + (2*1 + 3*0 + 4*(-1))
= 0 + 0 - 2 + 1 + 0 - 3 + 2 + 0 - 4
= -6

  8. 对位置(1, 2)的3x3区域进行卷积：

    (1*1 + 2*0 + 1*(-1)) + (2*1 + 3*0 + 2*(-1)) + (3*1 + 4*0 + 3*(-1))
= 1 + 0 - 1 + 2 + 0 - 2 + 3 + 0 - 3
= 0

  9. 对位置(1, 3)的3x3区域进行卷积：

    (2*1 + 1*0 + 0*(-1)) + (3*1 + 2*0 + 1*(-1)) + (4*1 + 3*0 + 2*(-1))
= 2 + 0 + 0 + 3 + 0 - 1 + 4 + 0 - 2
= 6

  10. 对位置(1, 4)的3x3区域进行卷积：

    (1*1 + 0*0 + 0*(-1)) + (2*1 + 1*0 + 0*(-1)) + (3*1 + 2*0 + 1*(-1))
= 1 + 0 + 0 + 2 + 0 + 0 + 3 + 0 - 1
= 5

  11. 对位置(2, 0)的3x3区域进行卷积：

    (0*1 + 1*0 + 2*(-1)) + (0*1 + 2*0 + 3*(-1)) + (0*1 + 3*0 + 4*(-1))
= 0 + 0 - 2 + 0 + 0 - 3 + 0 + 0 - 4
= -9

  12. 对位置(2, 1)的3x3区域进行卷积：

    (1*1 + 2*0 + 3*(-1)) + (2*1 + 3*0 + 4*(-1)) + (3*1 + 4*0 + 3*(-1))
= 1 + 0 - 3 + 2 + 0 - 4 + 3 + 0 - 3
= -4

  13. 对位置(2, 2)的3x3区域进行卷积：

    (2*1 + 3*0 + 2*(-1)) + (3*1 + 4*0 + 3*(-1)) + (4*1 + 3*0 + 2*(-1))
= 2 + 0 - 2 + 3 + 0 - 3 + 4 + 0 - 2
= 2

  14. 对位置(2, 3)的3x3区域进行卷积：

    (3*1 + 2*0 + 1*(-1)) + (4*1 + 3*0 + 2*(-1)) + (3*1 + 2*0 + 1*(-1))
= 3 + 0 - 1 + 4 + 0 - 2 + 3 + 0 - 1
= 6

  15. 对位置(2, 4)的3x3区域进行卷积：

    (2*1 + 1*0 + 0*(-1)) + (3*1 + 2*0 + 1*(-1)) + (4*1 + 3*0 + 2*(-1))
= 2 + 0 + 0 + 3 + 0 - 1 + 4 + 0 - 2
= 6

  16. 对位置(3, 0)的3x3区域进行卷积

  • 对位置 (0,0) 的3x3区域进行卷积（左上角）：

    (0*1 + 0*0 + 0*(-1)) + (0*1 + 0*0 + 1*(-1)) + (0*1 + 1*0 + 2*(-1))
= -3

  • 对位置 (0,1) 的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (0*1 + 1*0 + 2*(-1)) + (1*1 + 2*0 + 3*(-1))
= -4

  • 对位置 (0,2) 的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (1*1 + 2*0 + 1*(-1)) + (2*1 + 3*0 + 2*(-1))
= 0

  • 对位置 (0,3) 的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (2*1 + 1*0 + 0*(-1)) + (3*1 + 2*0 + 1*(-1))
= 4

  • 对位置 (0,4) 的3x3区域进行卷积：

    (0*1 + 0*0 + 0*(-1)) + (1*1 + 0*0 + 0*(-1)) + (2*1 + 1*0 + 0*(-1))
= 3

  • 对位置 (1,0) 的3x3区域进行卷积：

    (0*1 + 0*0 + 1*(-1)) + (0*1 + 1*0 + 2*(-1)) + (0*1 + 2*0 + 3*(-1))
= -6

  • 对位置 (1,1) 的3x3区域进行卷积：

    (0*1 + 1*0 + 2*(-1)) + (1*1 + 2*0 + 3*(-1)) + (2*1 + 3*0 + 4*(-1))
= -6

  • 对位置 (1,2) 的3x3区域进行卷积：

    (1*1 + 2*0 + 1*(-1)) + (2*1 + 3*0 + 2*(-1)) + (3*1 + 4*0 + 3*(-1))
= 0

以此类推，生成的特征图为：

[
 [-3, -4,  0,  4,  3],
 [-6, -6,  0,  6,  6],
 [-7, -6,  0,  6,  7],
 [-6, -6,  0,  6,  6],
 [-3, -4,  0,  4,  3]
]

激活函数ReLU

应用ReLU激活函数，将负值置为0：

[
 [0, 0,  0,  4,  3],
 [0, 0,  0,  6,  6],
 [0, 0,  0,  6,  7],
 [0, 0,  0,  6,  6],
 [0, 0,  0,  4,  3]
]

3. 第一个池化层

使用2x2最大池化，stride为2，padding为valid

池化操作计算

  1. 窗口覆盖区域 (0,0)到 (1,1)：

    [
    [0, 0],
    [0, 0]
    ]

最大值为0

  1. 窗口覆盖区域 (0,2)到 (1,3):

    [
    [0,4],
    [0,6]
    ]

最大值为6

  1. 窗口覆盖区域 (2,0)到 (3,1)

    [
    [0,0],
    [0,0]
    ]

最大值为0

  1. 窗口覆盖区域 (2,2)到 (3,3)

    [
    [0,6],
    [0,6]
    ]

最大值为6

最大池化结果：

[
 [0, 6],
 [0, 6]
]

4. 第二个卷积层

使用另一个3x3卷积核，stride为1，padding为same。假设水平边缘检测卷积核如下：

[
 [1, 1, 1],
 [0, 0, 0],
 [-1, -1, -1]
]

填充上述池化层输出：

[
[0,0,0,0]
[0,0,6,0]
[0,0,6,0]
[0,0,0,0]
]

卷积操作计算同前，生成新的特征图为：

[
 [-6, -6],
 [6, 6]
]

激活函数ReLU

应用ReLU激活函数，将负值置为0：

[
 [0, 0],
 [6, 6]
]

5. 第二个池化层

使用2x2最大池化，stride为2，padding为valid，输出为：

[
 [6]
]

6. 扁平层

将最后一个池化层的输出展平成一维向量：

[6]

7. 全连接层

假设全连接层有3个神经元，随机初始化权重和偏置，进行计算：

[1.176856*6 + b1, -0.25833628*6 + b2, 1.3403485*6 + b3]  # 假设b1, b2, b3均为0
= [7.0611362, -1.5500176, 8.042091]

8. 输出层

使用softmax函数将全连接层输出转换为概率分布：

softmax([7.0611362, -1.5500176, 8.042091])
= [exp(7.0611362)/sum, exp(-1.5500176)/sum, exp(8.042091)/sum]
= [0.5209936545215091, -0.11436535298620337, 0.5933716984646943]

预测类别为概率最大的类别，即数字2。

具体代码实现

python 复制代码 
import tensorflow as tf
from tensorflow.keras import layers, models
import numpy as np

# 创建一个示例输入
x_train = np.array([[
    [0, 1, 2, 1, 0],
    [1, 2, 3, 2, 1],
    [2, 3, 4, 3, 2],
    [1, 2, 3, 2, 1],
    [0, 1, 2, 1, 0]
]], dtype=np.float32)
x_train = x_train[..., np.newaxis]  # 添加通道维度

# 定义垂直边缘检测卷积核
vertical_kernel = np.array([
    [1,  0, -1],
    [1,  0, -1],
    [1,  0, -1]
], dtype=np.float32)

# 定义水平边缘检测卷积核
horizontal_kernel = np.array([
    [1,  1,  1],
    [0,  0,  0],
    [-1, -1, -1]
], dtype=np.float32)

# 将卷积核转换为4D张量
vertical_kernel = vertical_kernel.reshape((3, 3, 1, 1))
horizontal_kernel = horizontal_kernel.reshape((3, 3, 1, 1))

# 构建CNN模型
model = models.Sequential([
    layers.Conv2D(1, (3, 3), activation='relu', input_shape=(5, 5, 1), padding='same'),  # 没有激活函数
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(1, (3, 3), activation='relu', padding='same'),  # 没有激活函数
    layers.MaxPooling2D((2, 2)),
    layers.Flatten(),
    layers.Dense(3)  # 假设输出层有3个神经元
])

# 设置第一个卷积层的权重为垂直边缘检测卷积核
model.layers[0].set_weights([vertical_kernel, np.zeros(1)])  # np.zeros(1) 是偏置

# 设置第二个卷积层的权重为水平边缘检测卷积核
model.layers[2].set_weights([horizontal_kernel, np.zeros(1)])  # np.zeros(1) 是偏置

# 设置全连接层的权重和偏置
# 获取全连接层的输入大小（展平后的特征图大小）
model_temp = models.Sequential(model.layers[:-1])  # 去掉最后的 Dense 层
flatten_output = model_temp.predict(x_train)
flattened_size = flatten_output.shape[1]

print("Flatten层输出大小:", flattened_size)

# 定义全连接层的权重和偏置
dense_weights = np.random.normal(size=(flattened_size, 3)).astype(np.float32)  # 权重初始化
dense_biases = np.zeros(3, dtype=np.float32)  # 偏置初始化

# 设置全连接层的权重和偏置
model.layers[-1].set_weights([dense_weights, dense_biases])

# 前向传播
outputs = model(x_train)
print("输出层结果:", outputs.numpy())

# 使用softmax转换为概率分布
probabilities = tf.nn.softmax(outputs).numpy()
print("概率分布:", probabilities)

三、CNN模型训练代码实现

python 复制代码 
import tensorflow as tf
from tensorflow.keras import layers, models
import matplotlib.pyplot as plt

# 加载数据集（以CIFAR-10为例）
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0  # 数据归一化

# 构建模型
model = models.Sequential([
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.MaxPooling2D((2, 2)),
    layers.Conv2D(64, (3, 3), activation='relu'),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(10)
])

# 编译模型
model.compile(optimizer='adam',
              loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              metrics=['accuracy'])

# 训练模型
history = model.fit(x_train, y_train, epochs=10, 
                    validation_data=(x_test, y_test))

# 可视化训练结果
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label = 'val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0, 1])
plt.legend(loc='lower right')
plt.show()

# 评估模型
test_loss, test_acc = model.evaluate(x_test,  y_test, verbose=2)
print(f'Test accuracy: {test_acc}')

四、构建CNN模型时，各层的作用和意义

输入层（Input Layer）

  • 意义：定义输入数据的形状。对于图像数据，通常包括高度、宽度和通道数。
  • 示例 ：layers.Input(shape=(28, 28, 1)) 表示输入为 28x28 像素的灰度图像。

卷积层（Convolutional Layer）

  • 意义：应用卷积操作，通过局部连接和共享权重的方式提取局部特征。卷积层通过不同的滤波器（卷积核）对输入数据进行卷积操作，提取不同特征。
  • 示例 ：layers.Conv2D(32, (3, 3), activation='relu', padding='same') 表示使用32个3x3的卷积核进行卷积操作，ReLU作为激活函数，padding='same' 表示输出的大小与输入相同（填充边界以保持大小）。

激活函数层（Activation Layer）

  • 意义：引入非线性，使模型能够学习和表示更复杂的函数。常用的激活函数包括ReLU、Sigmoid、Tanh等。
  • 示例 ：layers.Activation('relu') 表示使用ReLU激活函数。

池化层（Pooling Layer）

  • 意义：通过下采样操作减少数据维度，保留重要特征，同时减少计算量和过拟合。常见的池化操作有最大池化（MaxPooling）和平均池化（AveragePooling）。
  • 示例 ：layers.MaxPooling2D((2, 2), strides=2, padding='valid') 表示使用2x2的池化窗口，步幅为2，padding='valid' 表示不填充边界。

扁平层（Flatten Layer）

  • 意义：将多维特征图展平成一维向量，以便全连接层处理。扁平层通常连接卷积层和全连接层。
  • 示例 ：layers.Flatten() 将多维输入展平成一维。

全连接层（Dense Layer）

  • 意义：连接所有输入和输出神经元，执行线性变换和激活函数。在模型的最后几层，通常使用全连接层来综合卷积层提取的特征。
  • 示例 ：layers.Dense(128, activation='relu') 表示一个有128个神经元的全连接层，使用ReLU激活函数。

Dropout 层（Dropout Layer）

  • 意义：在训练过程中随机丢弃一定比例的神经元，防止过拟合，提高模型的泛化能力。
  • 示例 ：layers.Dropout(0.5) 表示每个神经元有50%的概率被丢弃。

输出层（Output Layer）

  • 意义：提供最终的预测结果。对于分类任务，输出层通常使用Softmax激活函数来输出概率分布。
  • 示例 ：layers.Dense(10, activation='softmax') 表示一个有10个神经元的全连接层，使用Softmax激活函数，用于10分类任务。

五、优化器

卷积神经网络（CNN）的优化器是用于调整网络权重以最小化损失函数的算法。不同的优化器在处理学习率调整和梯度更新方面有所不同。

梯度

在深度学习中，梯度是损失函数相对于模型参数（权重和偏置）的导数。通过计算梯度，优化器可以调整模型的参数，使得损失函数逐步减小，从而提高模型的性能。

具体来说，梯度下降算法（Gradient Descent）是一种迭代优化算法，用于寻找损失函数的最小值。该算法通过以下步骤进行：

1. 计算损失函数的梯度：计算损失函数相对于每个模型参数的导数。
2. 更新模型参数：按照梯度的反方向更新模型参数，更新步长由学习率决定。
3. 迭代上述步骤：不断重复上述步骤，直到损失函数收敛或达到预设的迭代次数。

在深度学习中，梯度通常通过反向传播算法（Backpropagation）进行计算。反向传播算法利用链式法则（Chain Rule），从输出层开始，逐层计算每个参数的梯度。

以下是一些常用的优化器及其作用：

1. 随机梯度下降（SGD）

作用：SGD通过逐步调整网络权重，使得损失函数逐步减少。它在每次迭代中使用一个小批量（mini-batch）数据来计算梯度并更新权重。

python 复制代码 
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)

优点：

  • 简单易理解。
  • 对大规模数据集有效。

缺点：

  • 容易陷入局部最小值。
  • 收敛速度较慢。

2. 动量梯度下降（SGD with Momentum）

作用：在SGD的基础上增加了动量的概念，通过引入一个动量项，来加速收敛，并减少震荡。

python 复制代码 
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.9)

优点：

  • 加快收敛速度。
  • 减少损失函数在局部最小值处的震荡。

缺点：

  • 需要调节动量参数。

3. Nesterov 动量（Nesterov Momentum）

作用：在动量梯度下降的基础上，进行提前梯度计算，进一步提高优化效率。

python 复制代码 
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.9, nesterov=True)

优点：

  • 提前梯度计算，提高优化效率。
  • 更稳定的收敛。

缺点：

  • 需要调节动量参数。

4. 自适应梯度算法（Adagrad）

作用：自适应学习率优化器，根据参数的历史梯度自适应地调整学习率，对稀疏数据表现良好。

python 复制代码 
optimizer = tf.keras.optimizers.Adagrad(learning_rate=0.01)

优点：

  • 自适应调整学习率。
  • 对稀疏数据表现良好。

缺点：

  • 学习率可能会变得过小，导致模型停止训练。

5. RMSProp

作用：对Adagrad进行改进，防止学习率过小，通过指数加权移动平均来调整学习率。

python 复制代码 
optimizer = tf.keras.optimizers.RMSprop(learning_rate=0.001)

优点：

  • 保持学习率的稳定性。
  • 对处理非平稳目标（如RNN）有效。

缺点：

  • 需要调节衰减参数。

6. 自适应矩估计（Adam）

作用：结合了动量梯度下降和RMSProp的优点，自适应调整学习率，同时考虑了一阶矩和二阶矩估计。

python 复制代码 
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)

优点：

  • 收敛速度快。
  • 自适应调整学习率。
  • 默认参数效果良好。

缺点：

  • 对某些问题的泛化性能不如SGD。

7. Adam变体（如Adamax、Nadam）

作用：Adam的变体，针对特定问题做出改进。

python 复制代码 
optimizer = tf.keras.optimizers.Adamax(learning_rate=0.002)
optimizer = tf.keras.optimizers.Nadam(learning_rate=0.001)

优点：

  • 适用于不同的优化需求。
  • 结合了不同优化器的优点。

缺点：

  • 需要根据具体任务选择合适的变体。

选择优化器的建议

  • Adam 是最常用的优化器之一，适合大多数深度学习任务，尤其是初学者。
  • SGD with Momentum 适合需要控制训练过程、对大规模数据集进行训练的情况。
  • RMSProp 和 Adagrad 适合处理稀疏数据或梯度较稀疏的任务。
  • 在特定任务中，可以尝试不同的优化器，结合验证集结果选择最合适的优化器。

六、损失函数

在卷积神经网络（CNN）中，损失函数用于衡量模型预测值与真实值之间的差异。选择适当的损失函数对模型的训练和性能有重要影响。以下是常用的损失函数及其作用：

1. 均方误差（Mean Squared Error, MSE）

作用 ：主要用于回归任务，衡量预测值与真实值之间的平方差。
公式 ：

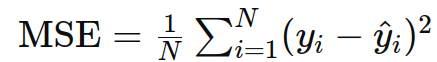
示例：

python 复制代码 
loss = tf.keras.losses.MeanSquaredError()

应用：回归任务，如房价预测、温度预测等。

2. 平均绝对误差（Mean Absolute Error, MAE）

作用 ：用于回归任务，衡量预测值与真实值之间的绝对差异。
公式 ：

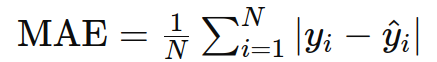
示例：

python 复制代码 
loss = tf.keras.losses.MeanAbsoluteError()

应用：回归任务，特别是对异常值不敏感的情况。

3. 二分类交叉熵（Binary Cross-Entropy）

作用 ：用于二分类任务，衡量预测概率分布与真实分布之间的差异。
公式 ：

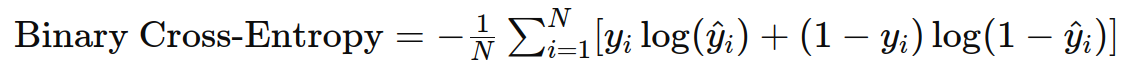
示例：

python 复制代码 
loss = tf.keras.losses.BinaryCrossentropy()

应用：二分类任务，如垃圾邮件分类、图像中的物体检测（是/否）。

4. 类别交叉熵（Categorical Cross-Entropy）

作用 ：用于多分类任务，衡量预测概率分布与真实分布之间的差异。
公式 ：

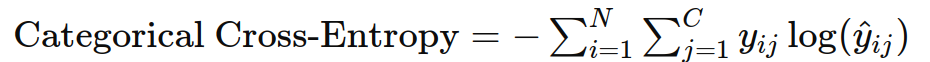
示例：

python 复制代码 
loss = tf.keras.losses.CategoricalCrossentropy()

应用：多分类任务，如手写数字识别（MNIST）、图像分类（CIFAR-10）。

5. 稀疏类别交叉熵（Sparse Categorical Cross-Entropy）

作用 ：类似于类别交叉熵，但标签是整数编码而不是one-hot编码。
公式：同类别交叉熵，但输入为整数标签。

示例：

python 复制代码 
loss = tf.keras.losses.SparseCategoricalCrossentropy()

应用：多分类任务，但标签为整数编码的情况。

6. Hinge 损失

作用 ：用于支持向量机（SVM）和最大边缘分类问题。
公式 ：

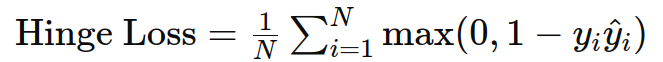
示例：

python 复制代码 
loss = tf.keras.losses.Hinge()

应用：二分类任务，通常用于支持向量机。

7. Kullback-Leibler 散度（Kullback-Leibler Divergence, KL Divergence）

作用 ：衡量两个概率分布之间的差异，常用于变分自编码器（VAE）等生成模型。
公式 ：

![外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fimg-blog.csdnim\[ \text{Contrastive Loss} %3D \frac{1}{2N} \sum_{i%3D1}^{N} (y_i d^2 %2B (1 - y_i\&pos_id=img-1FoRyRIB-1719285797153) \max(0, m - d)^2) ]

g.cn/direct/a8763aca2a7949e8b96773fd84b53ed4.png)
示例：

python 复制代码 
loss = tf.keras.losses.KLDivergence()

应用：概率分布比较，如生成模型中的分布匹配。

8. 对比损失（Contrastive Loss）

作用 ：用于度量学习，衡量成对样本之间的相似性。
公式 ：

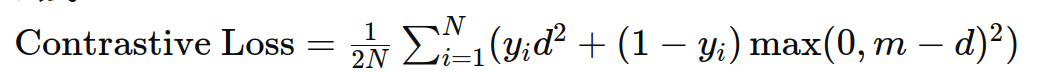
示例：

python 复制代码 
def contrastive_loss(y_true, y_pred):
    margin = 1
    return tf.reduce_mean(y_true * tf.square(y_pred) + (1 - y_true) * tf.square(tf.maximum(margin - y_pred, 0)))

应用：度量学习任务，如人脸识别中的 Siamese 网络。

实际应用中的损失函数选择

在实际应用中，选择损失函数应根据任务类型和数据特点来确定。以下是一些常见场景及其对应的损失函数：

  1. 图像分类：使用类别交叉熵（Categorical Cross-Entropy）或稀疏类别交叉熵（Sparse Categorical Cross-Entropy）。
  2. 图像分割：使用类别交叉熵或 Dice 损失（Dice Loss）。
  3. 物体检测：使用类别交叉熵和边界框回归损失（如 Smooth L1 Loss）的组合。
  4. 生成模型：使用 Kullback-Leibler 散度（KL Divergence）和对抗性损失（如 GAN 的生成器和判别器损失）。
  5. 回归任务：使用均方误差（MSE）或平均绝对误差（MAE）。

步骤5：实验与调优

  1. 调整超参数：改变卷积核大小、池化方式、层数等。
  2. 数据增强：使用图像翻转、旋转、缩放等方法增加训练数据。
  3. 正则化：使用Dropout层防止过拟合。

七、应用场景

卷积神经网络（CNN）在许多计算机视觉和其他领域有广泛的应用。以下是一些主要的应用场景：

1. 图像分类

  • 应用：识别图像中的对象类别。
  • 示例：手写数字识别（如MNIST）、猫狗分类、ImageNet大规模图像分类。
  • 方法：使用带有Softmax输出层的CNN来预测图像所属的类别。

2. 物体检测

  • 应用：在图像中检测并定位多个对象。
  • 示例：自动驾驶中的行人和车辆检测、安防监控中的异常检测。
  • 方法：使用区域卷积神经网络（R-CNN）、YOLO（You Only Look Once）、SSD（Single Shot Multibox Detector）等模型。

3. 图像分割

  • 应用：将图像划分为不同的区域，每个区域对应不同的类别。
  • 示例：医学图像分析中的器官分割、自动驾驶中的道路和车道分割。
  • 方法：使用全卷积网络（FCN）、U-Net、SegNet等模型。

4. 图像生成和图像修复

  • 应用：生成逼真的图像、修复损坏或缺失的图像部分。
  • 示例：生成对抗网络（GANs）用于生成艺术作品、修复老照片。
  • 方法：使用生成对抗网络（GANs）、变分自编码器（VAEs）等模型。

5. 图像风格迁移

  • 应用：将一种图像的风格应用到另一种图像上。
  • 示例：将梵高的画作风格应用到普通照片上。
  • 方法：使用卷积神经网络进行风格迁移，例如使用卷积神经网络进行风格迁移（Neural Style Transfer）。

6. 面部识别

  • 应用：识别和验证人脸。
  • 示例：安全系统中的人脸验证、社交媒体中的人脸标签、智能手机解锁。
  • 方法：使用深度学习模型，如VGG-Face、FaceNet等。

7. 视频分析

  • 应用：分析视频帧序列以识别活动或事件。
  • 示例：监控视频中的行为识别、体育赛事中的动作识别。
  • 方法：结合CNN和循环神经网络（RNN）或长短期记忆网络（LSTM），如使用3D-CNN、C3D等模型。

8. 自然语言处理

  • 应用：文本分类、情感分析、机器翻译。
  • 示例：情感分析中的正负情绪分类、垃圾邮件检测。
  • 方法：使用文本卷积神经网络（Text-CNN）、卷积神经网络与RNN结合的方法。

9. 医疗诊断

  • 应用：分析医学图像以辅助诊断。
  • 示例：X光片中的肺结核检测、MRI中的肿瘤识别。
  • 方法：使用训练有素的CNN模型进行图像分类、分割和检测。

10. 自动驾驶

  • 应用：环境感知，检测和识别道路上的物体。
  • 示例：自动驾驶汽车中的行人、交通标志、车道检测。
  • 方法：使用YOLO、R-CNN、FCN等模型进行实时对象检测和分割。

11. 遥感图像分析

  • 应用：从卫星图像中提取有用的信息。
  • 示例：土地覆盖分类、城市增长监测、灾害评估。
  • 方法：使用CNN进行图像分类和分割。

12. 体育运动分析

  • 应用：分析运动员的动作和比赛情况。
  • 示例：足球比赛中的球员追踪、动作分析。
  • 方法：结合CNN和LSTM进行视频分析和动作识别。

这些应用场景展示了CNN的广泛应用，尤其是在处理图像和视频数据方面。通过不断的发展和优化，CNN在各种实际问题中表现出色，并在许多领域取得了显著的进展。

相关推荐
钰爱&30 分钟前
【操作系统】Linux之线程同步二（头歌作业）
linux·运维·算法
BestSongC34 分钟前
基于YOLOv8模型的安全背心目标检测系统（PyTorch+Pyside6+YOLOv8模型）
人工智能·pytorch·深度学习·yolo·目标检测·计算机视觉
Ws＿34 分钟前
leetcode LCR 068 搜索插入位置
数据结构·python·算法·leetcode
灼华十一36 分钟前
数据结构-布隆过滤器和可逆布隆过滤器
数据结构·算法·golang
adam_life2 小时前
OpenJudge_ 简单英文题_04:0/1 Knapsack
算法·动态规划
龙的爹23333 小时前
论文翻译 | The Capacity for Moral Self-Correction in Large Language Models
人工智能·深度学习·算法·机器学习·语言模型·自然语言处理·prompt
鸣弦artha4 小时前
蓝桥杯——杨辉三角
java·算法·蓝桥杯·eclipse
我是聪明的懒大王懒洋洋4 小时前
力扣力扣力：动态规划入门（1）
算法·leetcode·动态规划
丶Darling.4 小时前
Day44 | 动态规划 ：状态机DP 买卖股票的最佳时机IV&&买卖股票的最佳时机III
算法·动态规划
Hoper.J4 小时前
用两行命令快速搭建深度学习环境（Docker/torch2.5.1+cu118/命令行美化+插件），包含完整的 Docker 安装步骤
人工智能·深度学习·docker
热门推荐
01智能车联网安全发展形势、挑战02Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04玄机平台应急响应—webshell查杀05软件工程从理论到实践客观题汇总(头歌第一章至第八章)06组基轨迹建模 GBTM的介绍与实现（Stata 或 R）07HP惠普星15青春版/惠普小欧笔记本电脑15s-du1008tx原装出厂Win11系统08全面解析：构建基于深度学习的安全帽检测系统（UI界面+YOLO代码+数据集）09基于YOLOv10深度学习的CT扫描图像肾结石智能检测系统【python源码+Pyqt5界面+数据集+训练代码】深度学习实战、目标检测10Python数据分析案例31——中国A股的月份效应研究(方差分析，虚拟变量回归)