文章目录
引言
- 今天应该是舟车劳顿的一天,头一次在机场刷题,不学习新的东西了,就复习一些之前学习的算法了。
复习
二维背包问题------宠物小精灵之收服
以往的分析链接

个人实现
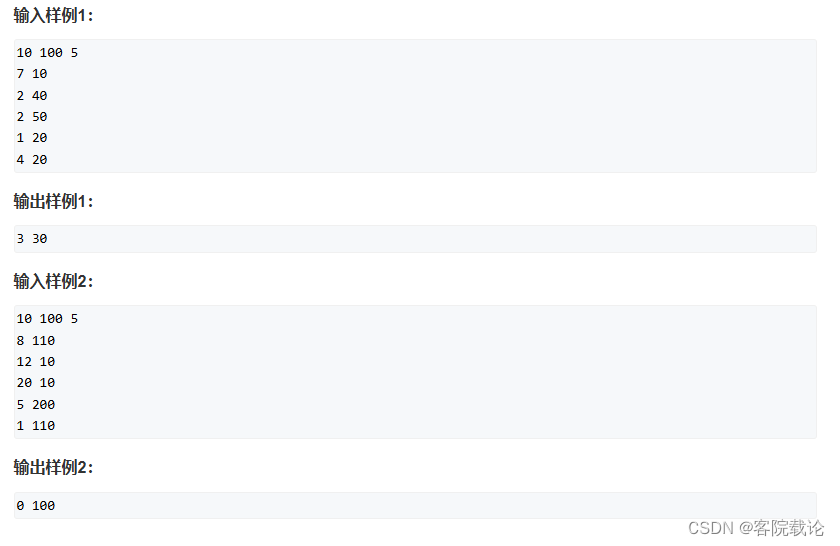
- 这是第二次在做这道题,这是一个单纯的二维背包问题,需要理清楚最后是要你输出什么类型,先给20分钟在开发网站上尝试一下,然后在来具体分析。
c
#include <iostream>
#include <cstring>
#include <limits.h>
using namespace std;
const int N = 1010,M = 550,K = 110;// 其中的N表示的精灵球的数量,M是体力值,K是野生精灵的数量
int nt[K],mt[K];
int f[K][N][M];
int n,m,k;
int main(){
cin>>n>>m>>k;
for(int i = 1;i <= k;i ++){
cin>>nt[i]>>mt[i];
}
// 二维背包问题计算状态转移矩阵变化的
int res = f[k][n][m-1];
for(int i = 1;i <= k;i ++){
// 针对第i个物体,只有判定抓或者不抓两种情况
for(int j = 0;j <= n;j ++){
// 遍历合法情况下的精灵球数量
for(int l = 0 ;l <= m - 1;l ++){
// 遍历合法情况下的体力值,注意上下确界,体力值不能消耗完
// 两种情况,抓或者是不抓,对应需要处理边界值的情况
if (j-nt[i] >= 0 && l-mt[i] >= 0)
f[i][j][l] = max(f[i-1][j][l],f[i-1][j-nt[i]][l-mt[i]] + 1);
else
f[i][j][l] = f[i-1][j][l];
res = max(f[i][j][l],res);
}
}
}
cout<<res<<" ";
// 第二个维度进行判定
for(int i = 1;i <= k;i ++) {
// 针对第i个物体,只有判定抓或者不抓两种情况
for (int j = 1; j <= n; j++) {
// 遍历合法情况下的精灵球数量
for (int l = 1; l <= m - 1; l++) {
if (f[i][j][l] == 2)
cout<<"("<<i<<","<<j<<","<<l<<"): "<<f[i][j][l]<<" "<<endl;
}
}
}
int cost_health = m;
for(int i = 0;i < m;i ++){
if(f[k][n][i] == res)
cost_health = min(cost_health,i);
}
cout<<m - cost_health;
}重大问题
- 这里有一个重要的发现,就是就是如果使用原始的,不加滚动数组优化的,就得保证每一层之间都能够将信息传递下来,不能因为不满足条件,就直接跳过。
- 这个bug看了好久,才发现,中间是断层的,之前的决策信息是没有传递下来的,所以最后一行都是空的。
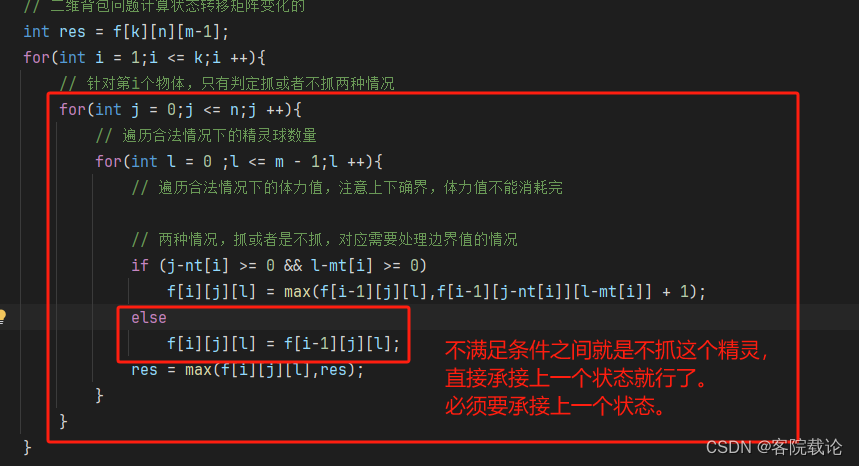
滚动数组优化实现
- 这里可以使用滚动数组进行优化实现,因为每一次都是从前往后遍历,然后用的是之前的数据。如果使用从后往前遍历,就不需要修改上一个数组了,这里讲的有点模糊,有点混乱。这里直接看我之前的分析吧,具体如下
- 背包模板------采药问题
- 设计公式推导,不过不重要,很好记:完全背包问题------买书
- 这个是公式推导的第二部分:完全背包问题------买书2
最终实现代码如下
- 实现起来真简单,不得不说,确实厉害!
c
#include <iostream>
#include <cstring>
#include <limits.h>
using namespace std;
const int N = 1010,M = 550,K = 110;// 其中的N表示的精灵球的数量,M是体力值,K是野生精灵的数量
int nt[K],mt[K];
int f[N][M];
int n,m,k;
int main(){
cin>>n>>m>>k;
for(int i = 1;i <= k;i ++){
cin>>nt[i]>>mt[i];
}
// 二维背包问题计算状态转移矩阵变化的
for(int i = 1;i <= k;i ++){
// 针对第i个物体,只有判定抓或者不抓两种情况
for(int j = n;j >= nt[i];j --){
// 遍历合法情况下的精灵球数量
for(int l = m - 1 ;l >= mt[i];l --){
f[j][l] = max(f[j][l],f[j-nt[i]][l-mt[i]] + 1);
}
}
}
int res = f[n][m-1];
cout<<res<<" ";
int cost_health = m;
for(int i = 0;i < m;i ++){
if(f[n][i] == res)
cost_health = min(cost_health,i);
}
cout<<m - cost_health;
}新作
串联所有单词的字串
- 题目链接


- 这题跳了好几次,后面好几题都做了,终于是他了,两天做这道题。
重点
- words是由若干个子字符串构成的,然后可以按照任意顺序进行拼接,形成n!个字符串,数量很大
- 每一个字符字串进行匹配查找拼接,这又是一个问题的。每个都是n平方的时间复杂度,根本做不了的。n平方 * n!,这个时间复杂度太高了。根本实现不了的!
- 可以在以下几个地方做出精简
- 扫描一次,然后记录所有相同长度,但是起点不同但是长度相同的字符串,然后在按照集合进行比较?这样确实能够缩减时间复杂度。
- 尝试使用不同的字符串进行优化?最长公共字串有用吗?KMP算法?不得行!
- 这样吧,匹配出每一个字符串在源字符串的位置,然后将源字符串标注为不同的序列,直接返回对应的序列即可。但是这里有一个问题的,就是这几个 word之间会出现嵌套的问题吗?如果出现嵌套问题就不好做了。
个人实现
- 字符串s重点长度为x的s.size() - x个子串中,和words中的每一个字符串进行匹配,然后进行标注。判定当前的字符串是相等的,过滤一遍的。记录一下,每一个元素开始的位置,然后再向后进行遍历,保证结果相同?
- 没有办法保证word和word之间是没有重叠的,这种情况肯定会出现,这就不知道怎么处理了。
- 不想做了,今天好烦躁呀,还是直接看解说吧。
参考实现
-
这里参考的y总的代码,基本思路还是很简答的,关键是如何将问题进行拆解,和我的思路比较像,但是有两个地方没有想到
- 字符串的快速匹配可以使用hash实现,这里我并没有考虑到,在我的设想里面只能使用遍历实现
- 两个字符字串的匹配使用两个hash表配合滑动窗口实现的
-
具体思路分析图如下
具体实现代码如下
c
#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
vector<int> findSubstring(string s,vector<string >& words){
vector<int> res;
// 边界条件判定为空
if (words.empty()) return res;
// 定义words的长度和word的长度,以及整个string的长度
int n = s.size(),m = words.size(),w = words[0].size();
// 定义目标子串中的对应的hash表
unordered_map<string,int> tot;
for (auto s:words) tot[s] ++;
// 将待匹配的原始的字符串进行等距分割拼接
for (int i = 0; i < w; ++i) {
// 定义count记录当前起点下的有效的字符子串的个数
int cnt = 0;
// 对每一个起点创建对应的字典字符串
unordered_map<string,int> temp;
for (int j = i; j < n; j += w) {
// 如果长度大于滑动窗口的长度,需要弹出
if (j >= i + m * w){
// 已经超过了长度,需要弹出最初的元素
auto st = s.substr(j - m * w,w);
temp[st] --;
// 判定弹出的元素是否有效
if (temp[st] < tot[st]) cnt--;
}
// 需要往队列中添加元素
auto st = s.substr(j ,w);
temp[st] ++;
// 判定加入的元素是否有效
if (temp[st] <= tot[st]) cnt ++;
if (cnt == m) res.push_back(j - (m - 1)*w );
}
}
return res;
}
int main(){
}总结
-
刚到上海,总是有很多东西需要收拾,本来准备来实习的,结果的主管面还是把我拒了,确实没有准备好呀,难受,现在就是单纯来学习的了。心里怅然若失!不过无所谓了,先做着吧,尽力去做着吧。来了弄了蛮多家务的,昨天的都没有交稿,脱了两天,明天开始进入状态了,调整一下,不能浪费时间!继续卷吧!然后开始继续弄的!
-
今天挫败感还是满足的,感觉坐立不安,怎么都不舒服。
- 换环境了?
- 没找到实习
-
都有吧,好好干吧!