红黑树插入删除流程(流程图)
红黑树性质
- 左根右(二叉树)
- 根叶黑(根节点是黑色的)
- 不红红(不存在相邻两个红色节点)
- 黑路同(对于每个节点,从该节点出发到任一空叶节点所经过的黑节点数目相同);
- 同时认为每个叶节点(NIL节点)是黑色
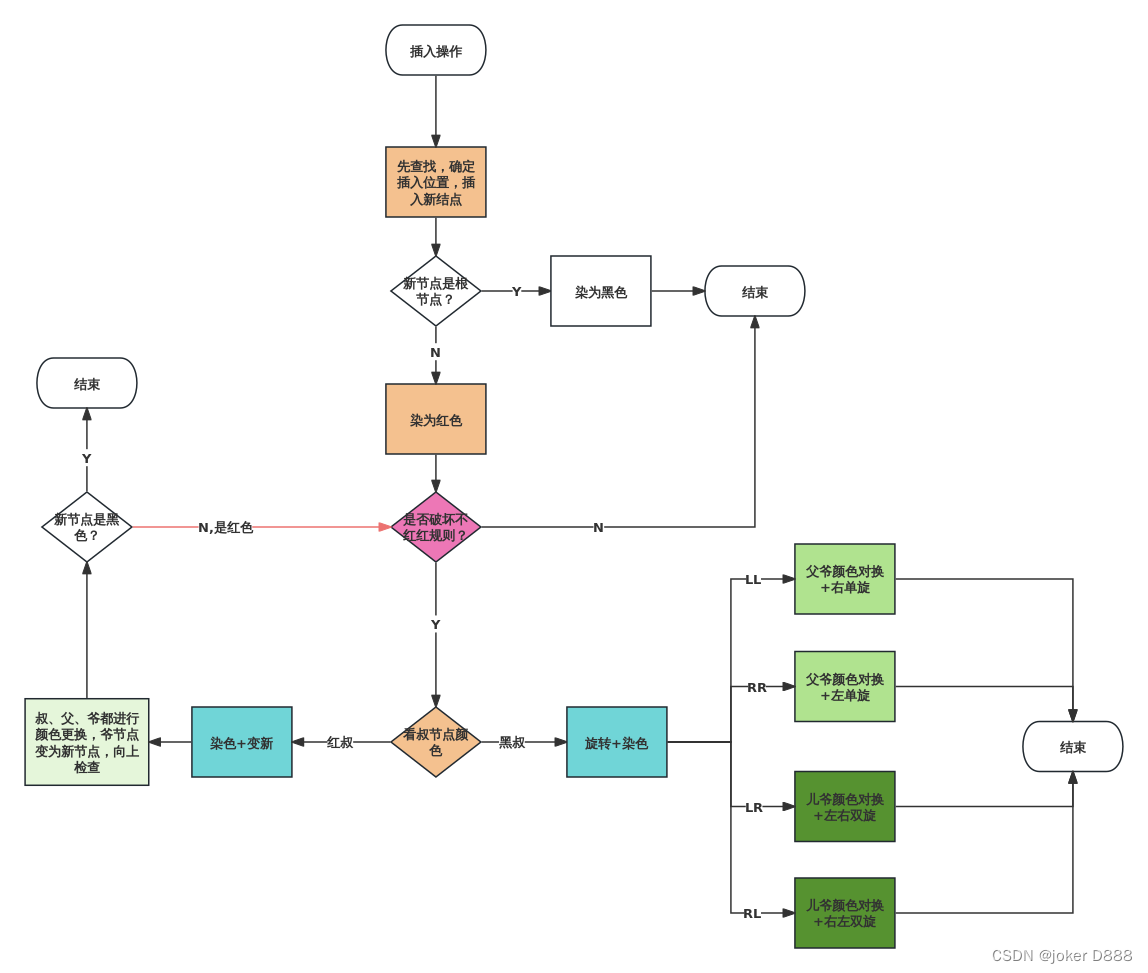
插入流程
- 首先按照二叉树排序树的规则确定要插入的位置(要插的位置一定是叶节点,即假设和二叉排序树一样不做调整,插入后一定是叶节点)
- 若新节点是根节点,染为黑色,结束
- 否则默认先染为红色,这时判断它的父节点是不是红色(是否破坏不红红规则)
- 若没有破坏不红红规则,结束
- 破坏了不红红规则(父节点是红色),接下来看叔叔节点的脸色行事
- 黑叔,旋转+染色:LL/RR型,父爷颜色对换+左/右单旋;LR/RL型,儿爷颜色对换+左右/右左双旋;结束
- 红树,染色+变新:叔、父、爷都进行颜色更换,爷点变为新节点,向上检查(若此时新节点为黑色则结束,若红色则重新开始以新节点的视角进行调整)
补充:当插入一个新节点时,因为新节点是红色的,因此可能会破坏性质3(没有两个相邻的红色节点)或性质2(根节点是黑色的),但不会破坏其他性质。所以除开新节点是根的情况,插入过程中只需要看是否破坏了"不红红"的规则。
删除流程
删除黑色节点的时候会破坏黑路同的规则,为了便于理解调整的过程,引入标记概念(当前是哪个点破坏了红黑树的规则),后面调整的时候的任务就是清除标记。所以说如果删除的是没有孩子的黑色节点,就会出现标记。
同时便于描述,记符号r为兄弟节点的红孩子,s为兄弟节点,p为父节点。此外,LL,RR型的节点情况和上方有些许不同:只要s是p的左孩子,r是s的左孩子,就是LL型(即使s有两个红节点);同样的,只要s是p的右孩子,r是s的右孩子,就是RR型(即使s有两个红节点)
- 先查找,确定要删除的节点,看要删除的节点是否是叶子节点?
- 不是叶子节点
- 左右子树都存在,则进行直接后继/前驱代替值,然后改为删除替换的节点,然后回到上一步看要删除的节点是否是叶子节点。
- 只有左孩子/右孩子,则用孩子代替后变黑,结束。(这里只有单个孩子的情况下,只能是当前节点是黑色,孩子是红色,不会是其他情况,否则就破坏了黑路同或者不红红的规则)
- 是叶子节点,则看节点的颜色?
- 红节点,直接删除,结束
- 黑节点,删除后变空节点,同时附上标记,接下来看兄弟的脸色行事?
- 红兄弟:兄父颜色对换,朝标记点旋转,回到上一步,继续看标记节点的脸色行事
- 黑兄弟,看兄弟有几个红孩子?
- 至少一个红孩子:看r,s,p形状(LL,RR,LR,RL)进行变色+旋转
- LL型:r变s,s变p,p变黑,右旋,清除标记
- RR型:r变s,s变p,p变黑,左旋,清除标记
- LR型:r变p,p变黑,左旋右旋,清除标记
- RL型:r变p,p变黑,右旋左旋,清除标记
- 没有红孩子:兄弟变红,标记向父转移,再看标记现在是否是红节点或根节点?
- 是红节点或根节点,节点直接变黑,清除标记
- 是黑节点,回到上上步,继续看标记节点的脸色行事
- 至少一个红孩子:看r,s,p形状(LL,RR,LR,RL)进行变色+旋转

实践
实践是检验真理的唯一标准。由于部分过程文字描述的不够形象,特别是旋转部分,所以推荐使用可视化红黑树进行对比学习,点这里。
这里给出数据进行学习:
- 插入:20,10,5,30,40,57,3,2,4,35,25,18,22,23,24,19,18
- 删除:先构建出来{15,9,18,6,13,17,27,10,23,34,25,37},再按一下顺序删除{18,25,15,6,13,37,27,17,34,9,10,23}
推荐学习资源: