文章目录
-
- [Model-Based RL](#Model-Based RL)
-
-
- [Basics of Model-based reinforcement learning](#Basics of Model-based reinforcement learning)
- [Uncertainty of Model-based RL](#Uncertainty of Model-based RL)
- [Use uncertainty in Model-based RL](#Use uncertainty in Model-based RL)
- [State space (latent space) models](#State space (latent space) models)
-
Model-Based RL
Basics of Model-based reinforcement learning
Model-based reinforcement learning: If we know f ( s t , a t ) = s t + 1 f(s_t,a_t)=s_{t+1} f(st,at)=st+1 or p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t) p(st+1∣st,at) in the stochastic case, we can plan it better.
So let's learn f ( s t , a t ) f(s_t,a_t) f(st,at) from data, and then plan through it!
Model-based reinforcement learning version 0.5:
- run base policy π 0 ( s t ∣ s t ) \pi_0(s_t|s_t) π0(st∣st) (e.g., random policy) to collect some data D = { ( s , a , s ′ ) i } \mathcal{D}=\{(s,a,s')_i\} D={(s,a,s′)i}
- learn dynamics model f ( s , a ) f(s,a) f(s,a) to minimize ∑ i ∣ ∣ f ( s i , a i ) − s i ′ ∣ ∣ 2 \sum_i||f(s_i,a_i)-s'_i||^2 ∑i∣∣f(si,ai)−si′∣∣2 (监督学习)
- plan through model f ( s , a ) f(s,a) f(s,a) to choose actions
但这个version 0.5并不适应于一些场景:要拟合的模型参数过多的时候,如神经网络这种高容量的模型
Model-based reinforcement learning version 1.0:
- run base policy π 0 ( s t ∣ s t ) \pi_0(s_t|s_t) π0(st∣st) (e.g., random policy) to collect some data D = { ( s , a , s ′ ) i } \mathcal{D}=\{(s,a,s')_i\} D={(s,a,s′)i}
- learn dynamics model f ( s , a ) f(s,a) f(s,a) to minimize ∑ i ∣ ∣ f ( s i , a i ) − s i ′ ∣ ∣ 2 \sum_i||f(s_i,a_i)-s'_i||^2 ∑i∣∣f(si,ai)−si′∣∣2 (监督学习)
- plan through model f ( s , a ) f(s,a) f(s,a) to choose actions
- execute those actions and add the resulting data { ( s , a , s ′ ) i } \{(s,a,s')_i\} {(s,a,s′)i} to D \mathcal{D} D
- 重复2-4
改变的点,就是不断增加新的数据,能够变得可行一些了。
Can we do better?
如果我们的model有一些错误,如在实际上车的方向盘有一点偏左。v 1.0版本的算法能够修改model去纠正这个错误,但是需要过很长时间,因为我们用一个 f ( s , a ) f(s,a) f(s,a)执行了很多步以后才再迭代,我们需要来个更快纠错的算法:当发生错误的时候,立刻replan------先看一下采取action实际导致的state,随后问一下model这样的是不是想要的,而不是继续执行以前的
Model-based reinforcement learning version 1.5:(模型预测控制)
- run base policy π 0 ( s t ∣ s t ) \pi_0(s_t|s_t) π0(st∣st) (e.g., random policy) to collect some data D = { ( s , a , s ′ ) i } \mathcal{D}=\{(s,a,s')_i\} D={(s,a,s′)i}
- learn dynamics model f ( s , a ) f(s,a) f(s,a) to minimize ∑ i ∣ ∣ f ( s i , a i ) − s i ′ ∣ ∣ 2 \sum_i||f(s_i,a_i)-s'_i||^2 ∑i∣∣f(si,ai)−si′∣∣2 (监督学习)
- plan through model f ( s , a ) f(s,a) f(s,a) to choose actions
- execute the fist planned action, observe resulting state s ′ s' s′。只执行第一个动作,看看实际的结果是什么样的
- append ( s , a , s ′ ) (s,a,s') (s,a,s′) to dataset D \mathcal{D} D
- 立刻replan,重复3-5
- 重复2-5
所以整个方法的核心思想就是:我先试运行一部action看看效果怎么样(如果发现了汽车再偏左),那就重新plan得到action。实际上,重新plan的代价非常高,所以在第3步的时候,步伐小一些。
Uncertainty of Model-based RL
想象现在有这样一个场景:你训练一个RL模型在悬崖边行走,如果我们的 f ( s , a ) f(s,a) f(s,a)不对下一个具体状态进行预测而是下一个状态可能的分布,就像你会估计自己还有多远就会掉下悬崖,那么你更有可能到达紧挨着的边缘。如果你保持较小范围的不确定性,对自己的模型有很大的信心,那你会努力靠近;如果你有较大的不确定性,那么就会保持远离悬崖,因为更近的状态不确定。

the model is certain about the data, but we are not certain about the model

我们不去预测 p ( θ ∣ D ) p(\theta|D) p(θ∣D)最大值的 θ \theta θ而是试图直接预测它的分布, p ( θ ∣ D ) p(\theta|D) p(θ∣D)意味着模型的不确定性。随后我们在得到下一个状态的时候,就不是根据最大的 θ \theta θ,而是利用它的分布 去求一个期望。
∫ p ( s t + 1 ∣ s t , a t , θ ) p ( θ ∣ D ) d θ \int p(s_{t+1}|s_t,a_t,\theta)p(\theta|D)d\theta ∫p(st+1∣st,at,θ)p(θ∣D)dθ
举例子:贝叶斯神经网络
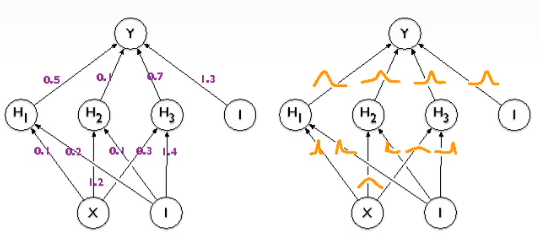
以往情况下,节点之间的连接都是确定的数,但是如果我们将它换成带有不确定性的分布,这个神经网络本身就具有了不确定性 。
当然,我们去得到这个维度很高的整个模型的参数分布的比较困难的,因此进行了一些简化:我们用每条边上的分布参数乘积去拟合,这默认了边上的分布之间是独立的:
p ( θ ∣ D ) = ∏ i p ( θ i ∣ D ) p ( θ i ∣ D ) = N ( μ i , σ i ) \begin{align}p(\theta|D)=\prod_ip(\theta_i|D)\\ p(\theta_i|D)=\mathcal{N}(\mu_i,\sigma_i)\end{align} p(θ∣D)=i∏p(θi∣D)p(θi∣D)=N(μi,σi)
边上的权重参数分布我们用高斯分布去拟合:以往的一个数的权重,现在用两个参数的分布函数来刻画不确定性, μ i \mu_i μi代表确定的参数值, σ i \sigma_i σi代表对这个参数的不确定性。
Bootstrap ensembles

实际上,我们需要这些模型相对独立的训练,SGD这种对数据集的随机采样就能够满足了。让他们投票下一个state是什么,他们之间投票的误差就能够实现一些不确定性估计。
Use uncertainty in Model-based RL
Before: J ( a 1 , ... , a H ) = ∑ t = 1 H r ( s t , a t ) J(a_1,\dots,a_H)=\sum_{t=1}^Hr(s_t,a_t) J(a1,...,aH)=∑t=1Hr(st,at), where s t + 1 = f ( s t , a t ) s_{t+1}=f(s_t,a_t) st+1=f(st,at), a 1 , ... , a H a_1,\dots,a_H a1,...,aH表示一个动作序列
Now: J ( a 1 , ... , a H ) = 1 N ∑ i = 1 N ∑ t = 1 H r ( s t , i , a t ) J(a_1,\dots,a_H)=\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^Hr(s_{t,i},a_t) J(a1,...,aH)=N1∑i=1N∑t=1Hr(st,i,at), where s t + 1 , i = f i ( s t , i , a t ) s_{t+1,i}=f_i(s_{t,i},a_t) st+1,i=fi(st,i,at)
一般情况下,对于候选的动作序列 a 1 , ... , a H a_1,\dots,a_H a1,...,aH:
- 采样模型 θ ∼ p ( θ ∣ D ) \theta\sim p(\theta|D) θ∼p(θ∣D),如果用了上面的Bootstrap 就想到于从N个模型中随机选一个
- 在每一个时间步长t, 采样状态 s t + 1 ∼ p ( s t + 1 ∣ s t , a t , θ ) s_{t+1}\sim p(s_{t+1}|s_t,a_t,\theta) st+1∼p(st+1∣st,at,θ),
- 计算所有时间上的奖励综合 R = ∑ t r ( s t , a t ) R=\sum_tr(s_t,a_t) R=∑tr(st,at)
- 重复1-3计算平均奖励
State space (latent space) models
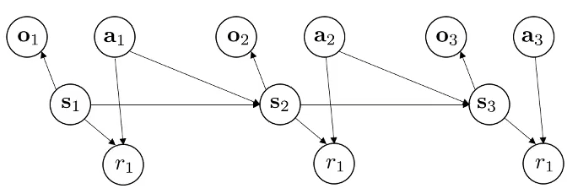
我们需要学: p ( s t ∣ s t ) p(s_t|s_t) p(st∣st)------观测模型 observation model
p ( s t + 1 ∣ s t , a t ) p(s_{t+1}|s_t,a_t) p(st+1∣st,at)------状态转移模型 dynamics model
p ( r t ∣ s t , a t ) p(r_{t}|s_t,a_t) p(rt∣st,at)------奖励模型 reward model
standard (fully oberved) model:
max ϕ 1 N ∑ i = 1 N ∑ t = 1 T log p ϕ ( s t + 1 , i ∣ s t , i , a t , i ) \max_{\phi}\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\log p_{\phi}(s_{t+1,i}|s_{t,i},a_{t,i}) ϕmaxN1i=1∑Nt=1∑Tlogpϕ(st+1,i∣st,i,at,i)
现在我们有了一个潜在空间latent space model:
max ϕ 1 N ∑ i = 1 N ∑ t = 1 T E [ log p ϕ ( s t + 1 , i ∣ s t , i , a t , i ) + log p ϕ ( o t , i ∣ s t , i ) ] \max_{\phi}\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^TE[\log p_{\phi}(s_{t+1,i}|s_{t,i},a_{t,i})+\log p_{\phi}(o_{t,i}|s_{t,i})] ϕmaxN1i=1∑Nt=1∑TE[logpϕ(st+1,i∣st,i,at,i)+logpϕ(ot,i∣st,i)]
如果我们知道状态s_t,上面这个式子会很容易,但问题是我们不知道,因此我们只能用未来状态的期望:expectation w.r.t. ( s t , s t + 1 ) ∼ p ( s t , s t + 1 ∣ o 1 : T , a 1 : T ) (s_t,s_{t+1})\sim p(s_t,s_{t+1}|o_{1:T},a_{1:T}) (st,st+1)∼p(st,st+1∣o1:T,a1:T)
我们想学习后验概率approximate posterior q ψ ( s t ∣ o 1 : t , a 1 : t ) q_{\psi}(s_t|o_{1:t},a_{1:t}) qψ(st∣o1:t,a1:t),这个也是一个神经网络encoder,给我们基于当前观测和动作,下一个状态的分布 ,这个神经网络有很多选择,我们在这里选择最简单的一个 q ψ ( s t ∣ o t ) q_{\psi}(s_t|o_t) qψ(st∣ot),这代表状态几乎可以从观测推断出来,因此它是一个确定编码器deterministic ,expectation w.r.t. s t ∼ q ψ ( s t ∣ o t ) , s t + 1 ∼ q ψ ( s t + 1 ∣ o t + 1 ) s_t\sim q_{\psi}(s_t|o_t),s_{t+1}\sim q_{\psi}(s_{t+1}|o_{t+1}) st∼qψ(st∣ot),st+1∼qψ(st+1∣ot+1)也就是说我们有 q ψ ( s t ∣ o t ) = δ ( s t = q ψ ( o t ) ) ⇒ s t = g ψ ( o t ) q_{\psi}(s_t|o_t)=\delta(s_t=q_{\psi}(o_t))\Rightarrow s_t=g_{\psi}(o_t) qψ(st∣ot)=δ(st=qψ(ot))⇒st=gψ(ot),目标函数变成:
max ϕ 1 N ∑ i = 1 N ∑ t = 1 T log p ϕ ( g ψ ( o t + 1 , i ) ∣ g ψ ( o t , i , a t , i ) + log p ϕ ( o t , i ∣ g ψ ( o t , i ) ) \max_{\phi}\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^T\log p_{\phi}(g_{\psi}(o_{t+1,i})|g_{\psi}(o_{t,i},a_{t,i})+\log p_{\phi}(o_{t,i}|g_{\psi}(o_{t,i})) ϕmaxN1i=1∑Nt=1∑Tlogpϕ(gψ(ot+1,i)∣gψ(ot,i,at,i)+logpϕ(ot,i∣gψ(ot,i))
整个上面的这些东西,都是为了在不知道状态的情况下,实现我们的优化,现在这个式子是可微可以用反向传播求解了。
!NOTE\] 小结 如果要去学习一个基于随机状态的模型,需要取对数期望而不是直接取期望,为了得到后验概率的近似,我们用最简单的,一个直接从观测得到状态的确定编码器,这种情况下,期望实际上不需要了,我们可以直接用编码器来代替状态在 observation model和 dynamics model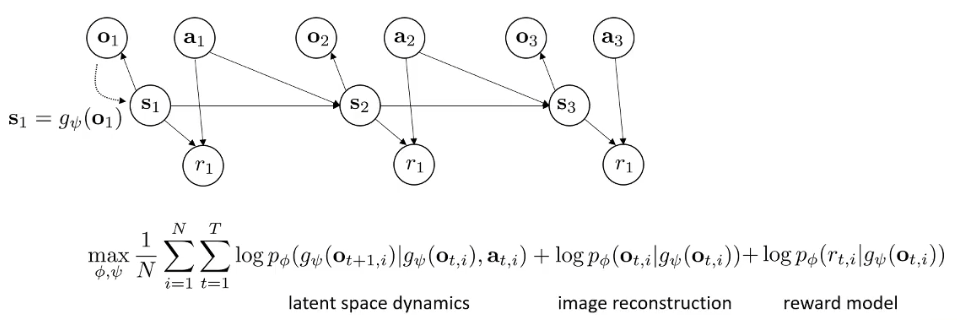
体现在RL算法中就是如下,整个过程中没有出现状态,只有观测:

Key idea: learn embedding g ( o t ) = s t g(o_t)=s_t g(ot)=st,或者直接学习 p ( o t + 1 ∣ o t , a t ) p(o_{t+1}|o_t,a_t) p(ot+1∣ot,at)