回归树:
表达式为T(x)=wq(x),意思为:一个样本x,落到树的哪个叶子结点由q(x)得出,具体叶子结点对应的值由w函数得出
如何构建函数:

运用加法模型构建,由T个基学习器构成,也可表示为前T-1个树的结果再加上第T个树的结果
前向分步算法:一种贪心算法,每次只优化当前树至最优结果
下面写目标函数:
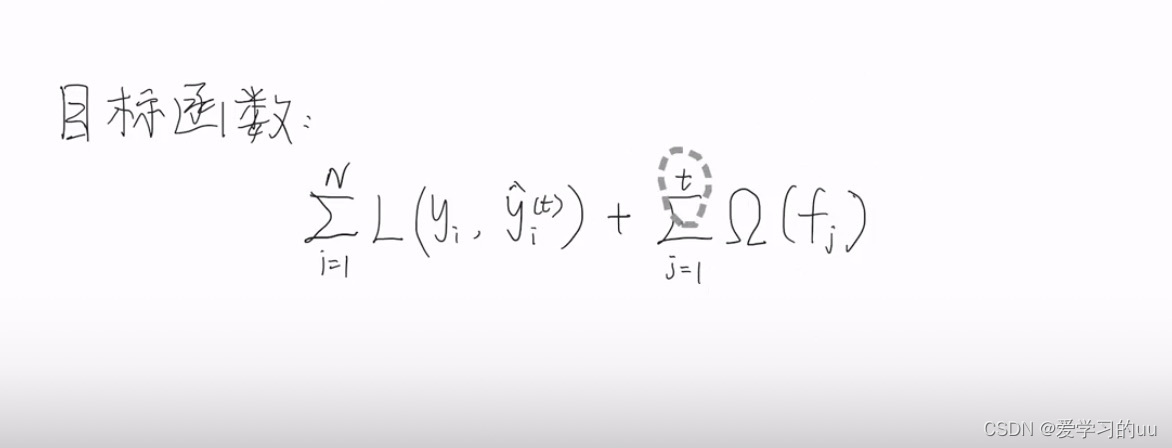
即为N个样本的损失函数总和加上正则项,其中正则项是t个模型复杂度的总和,目标是让这个函数最小
正则项如何展开:
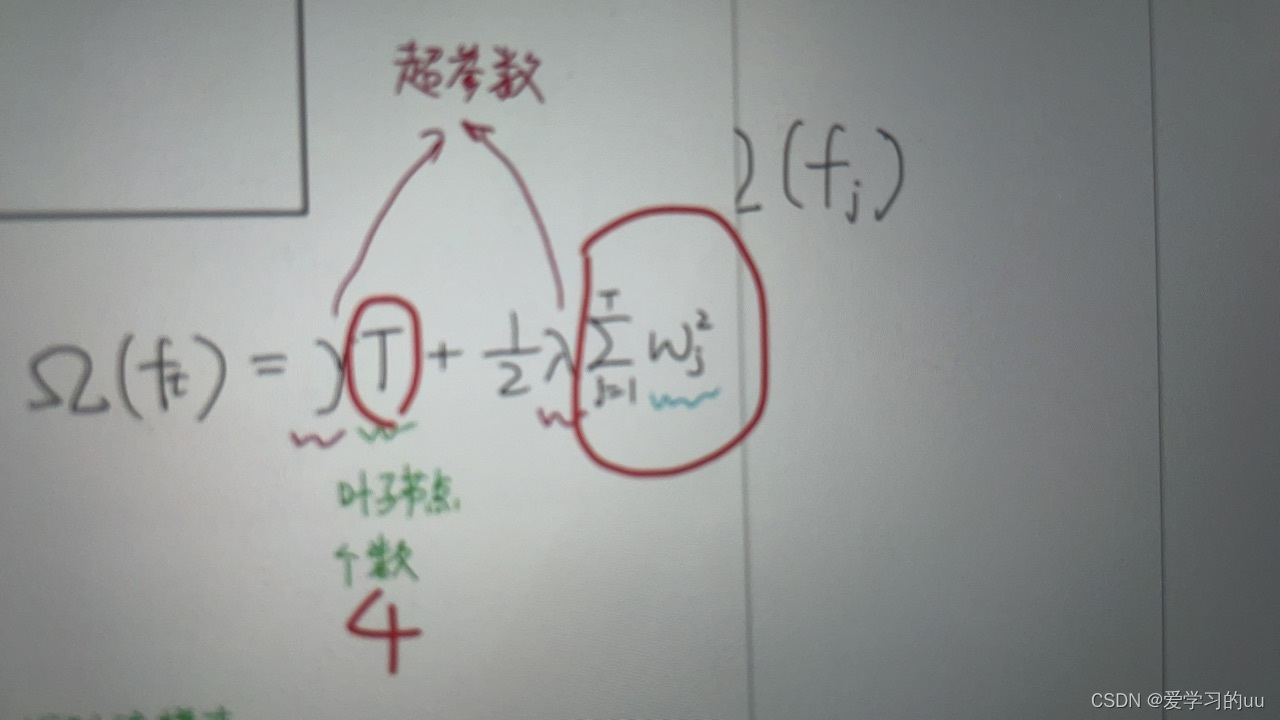
T是所有叶子结点的个数,w是叶子结点值平方和
如果某棵回归树值的占比较大,则容易过拟合。
再讲下第一部分的处理
一般可以用梯度下降来处理第一部分,但树模型是阶跃的(x<0一个值大于0一个值),不能这么搞
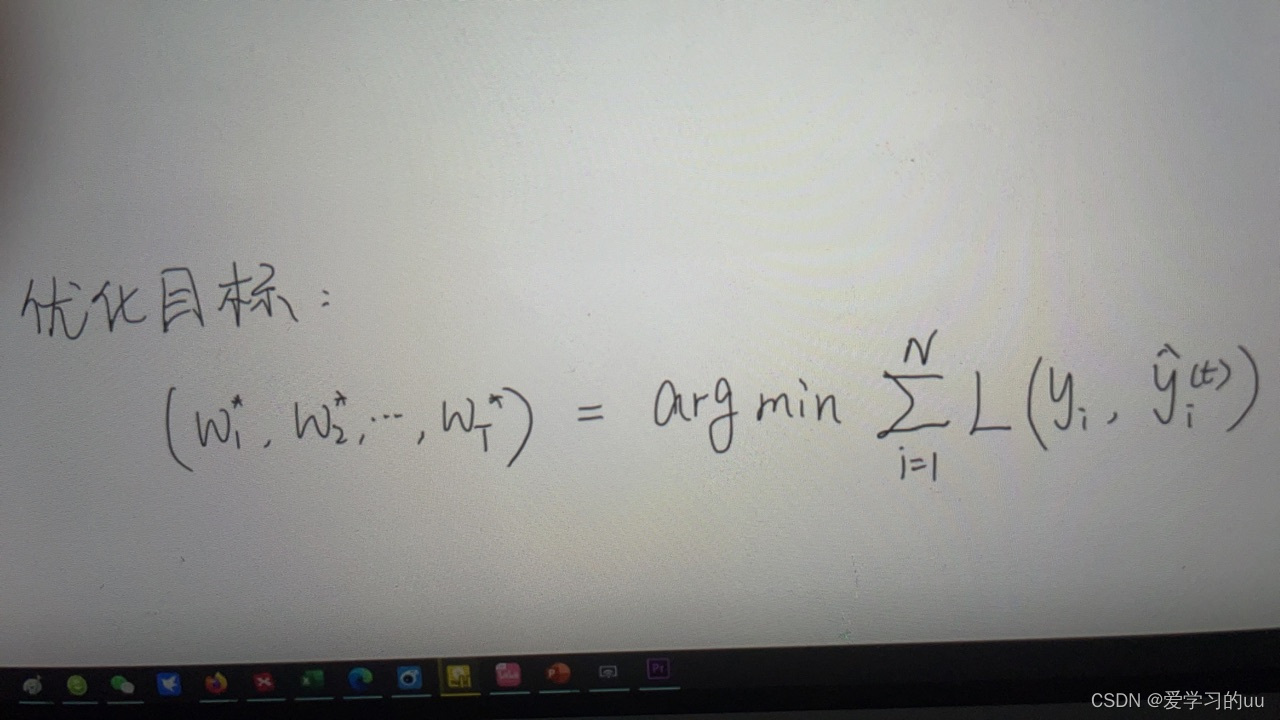
思路:把每一个样本的损失和变换为每个叶子结点的损失和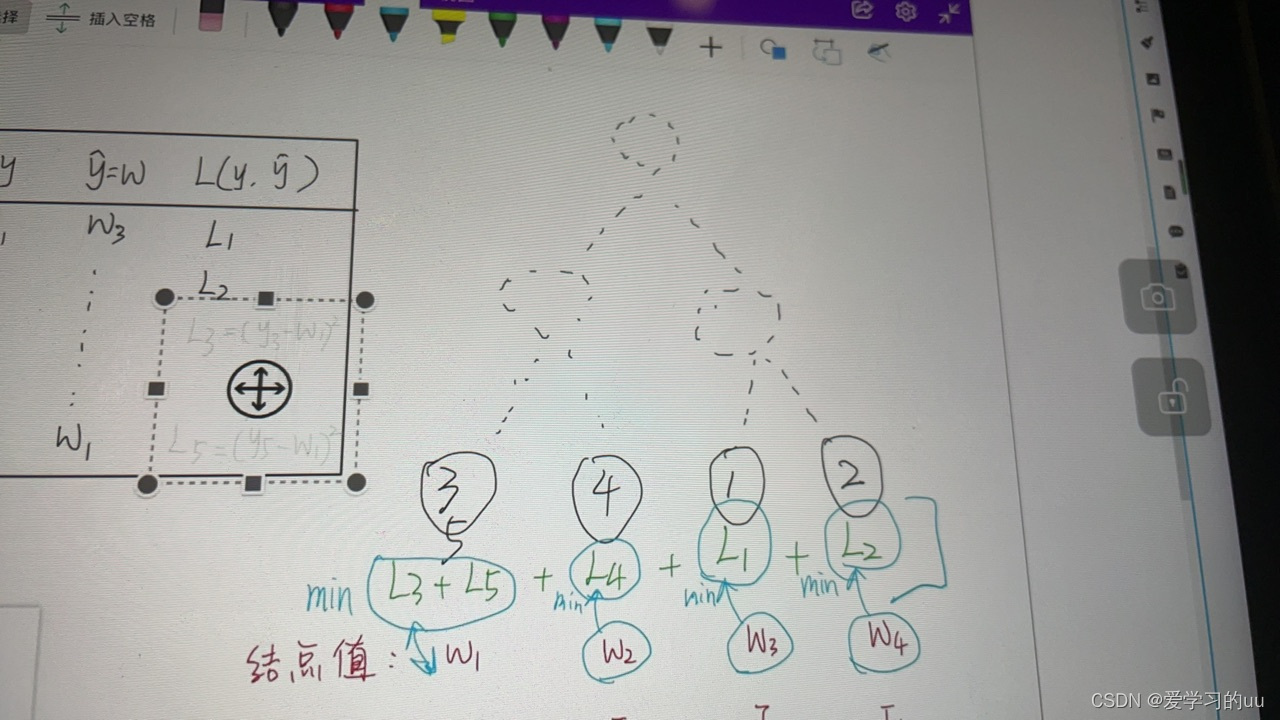
比如L结点1=L3+L5=(y3-w1)2+(y5-w1)2

求解得w=y3+y5时能取最小值
因此可以把公式变形为: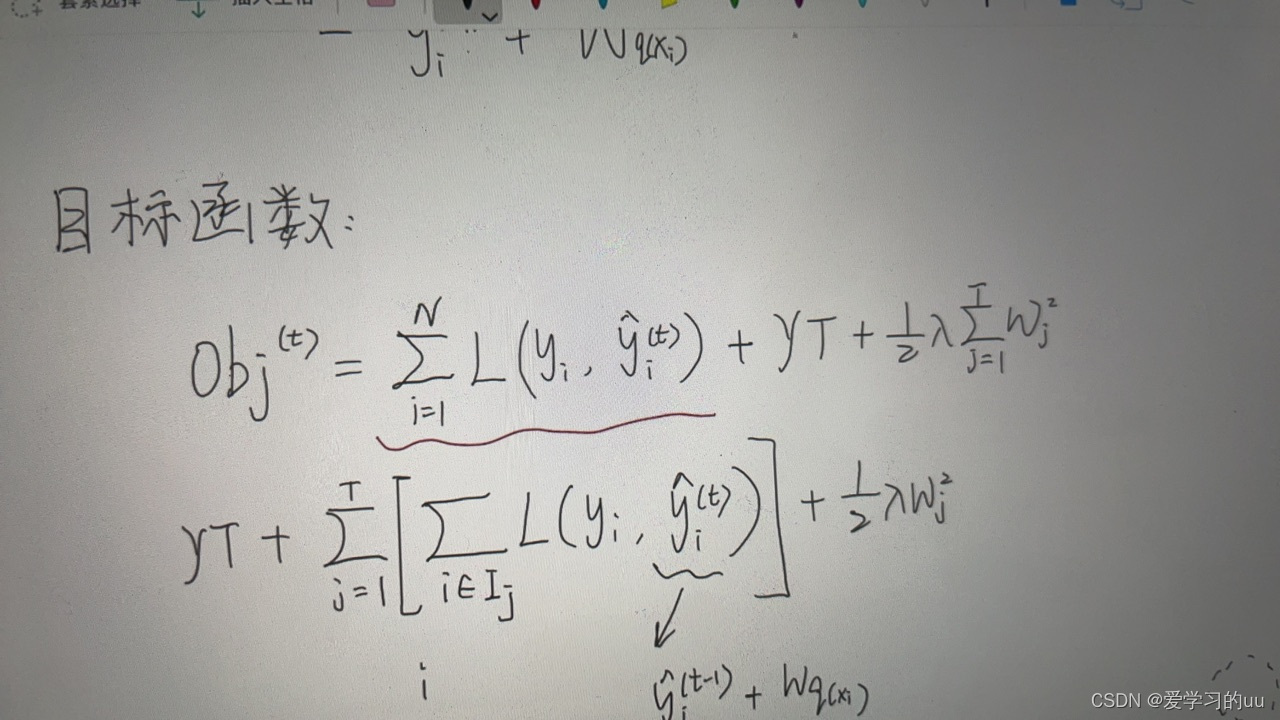
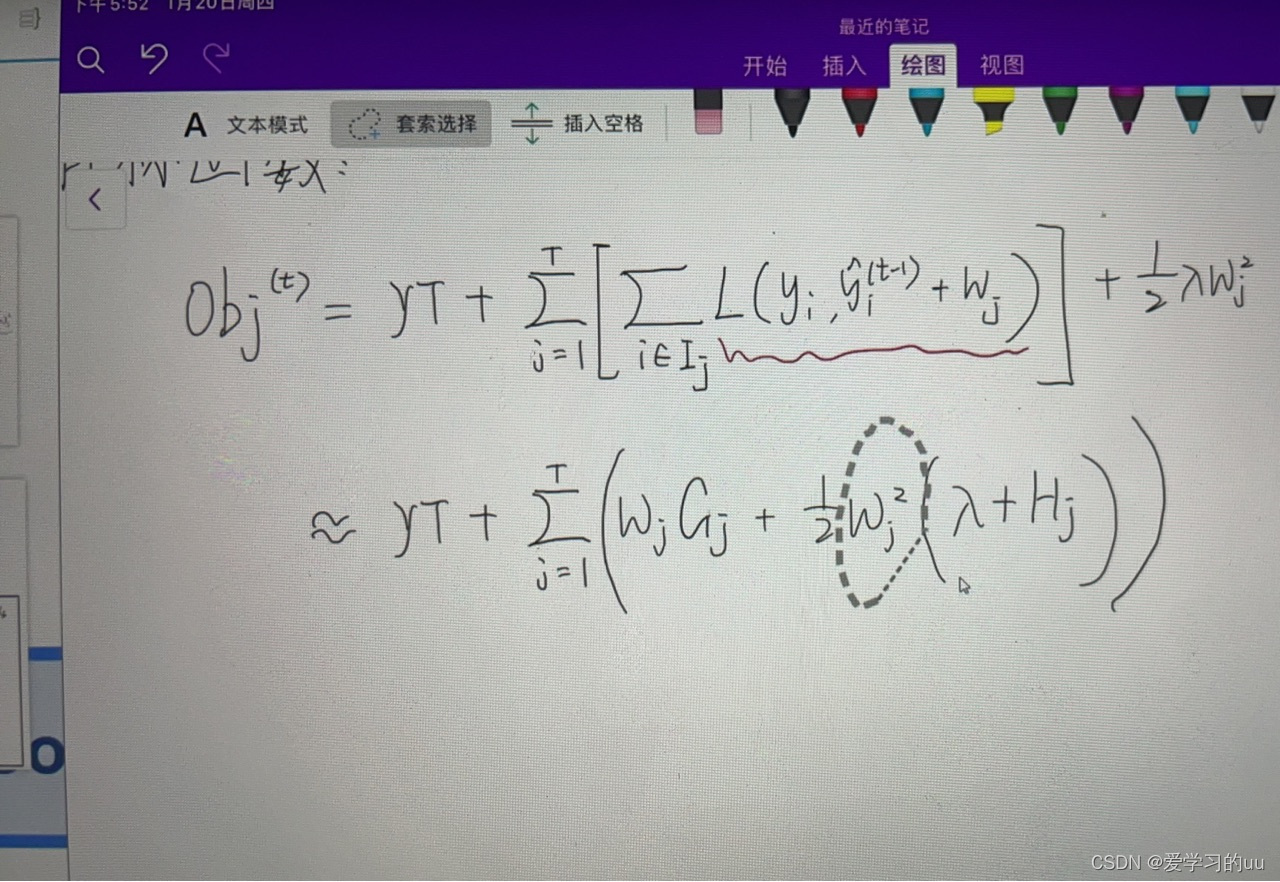
用二阶泰勒展开可得最终需要优化的表达式如上图,由此对每个变量w求最优解

有二次方程公式推出:
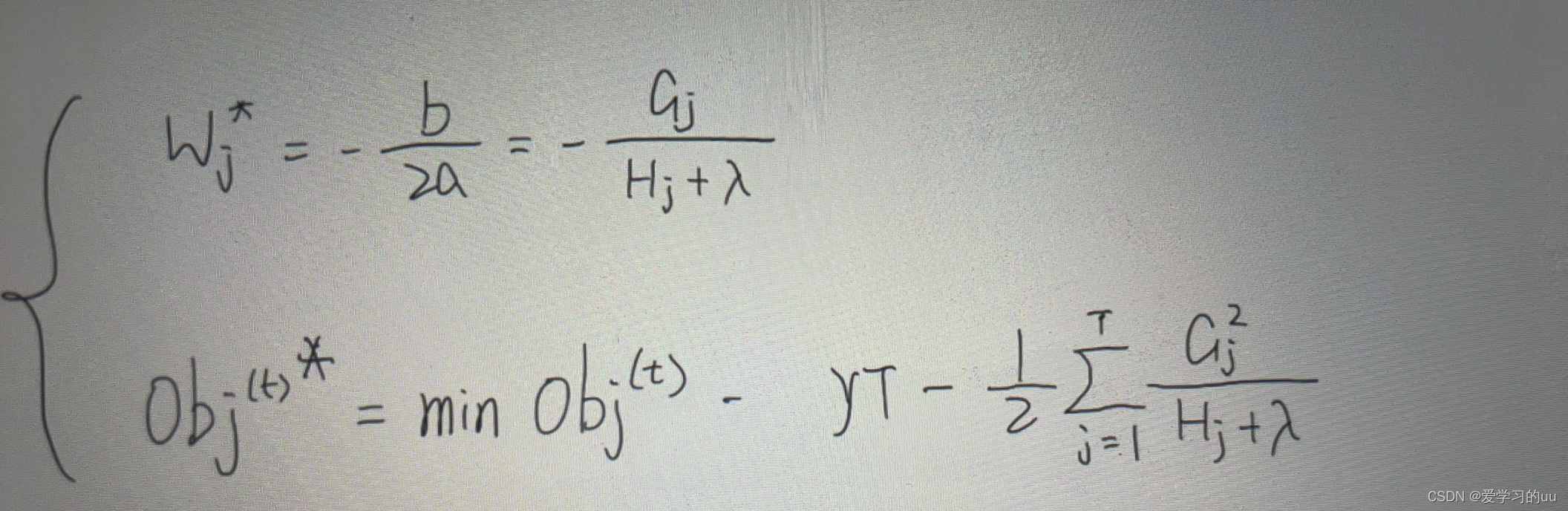
那么就可以得到思路:每次拿到一个数据集,就可以把它的一阶梯度和二阶梯度gh,再得到每个叶子结点的GH,再由上面公式把叶子结点的值都计算出来
那么接下来就是如何确定树的结构能让obj最小
法1:暴力穷举
法2:精确贪心:每次只关注一个节点如何做分裂,计算分裂后增益最大的划分
停止生长:增益均<=0,叶子结点包含样本数小于等于1,层级,叶子结点个数
算法实现:

I:样本集合 d:特征维度 gain:增益
k:遍历树
(注意可以并行计算,所以不会太慢,但是每次要根据不同的特征进行样本的排序,花时间)
优化:1.减少特征数(列采样)-按树/层随机选特征
2.每个特征下能不能减少特征值:分桶,每个桶样本数基本一致。改进方法是根据损失函数找加权分位点
即有hi个这个元素的样本 ,再按分桶方法去均匀分
策略上分为全局策略和局部策略,全局指一开始订好了3.5.7来分桶,则之后所有结点都按这三个值分,这很容易导致划到一定程度就化不下去了
而局部策略则是每个特征划分的特征值都不一样
接下来讲xgboost的缺失值处理:
有些特征不知道,但是样本id、gi、hi这些都能知道。处理方法是将缺失样本全部放到某一支,比较gain,放到最大的那支里
学习率:
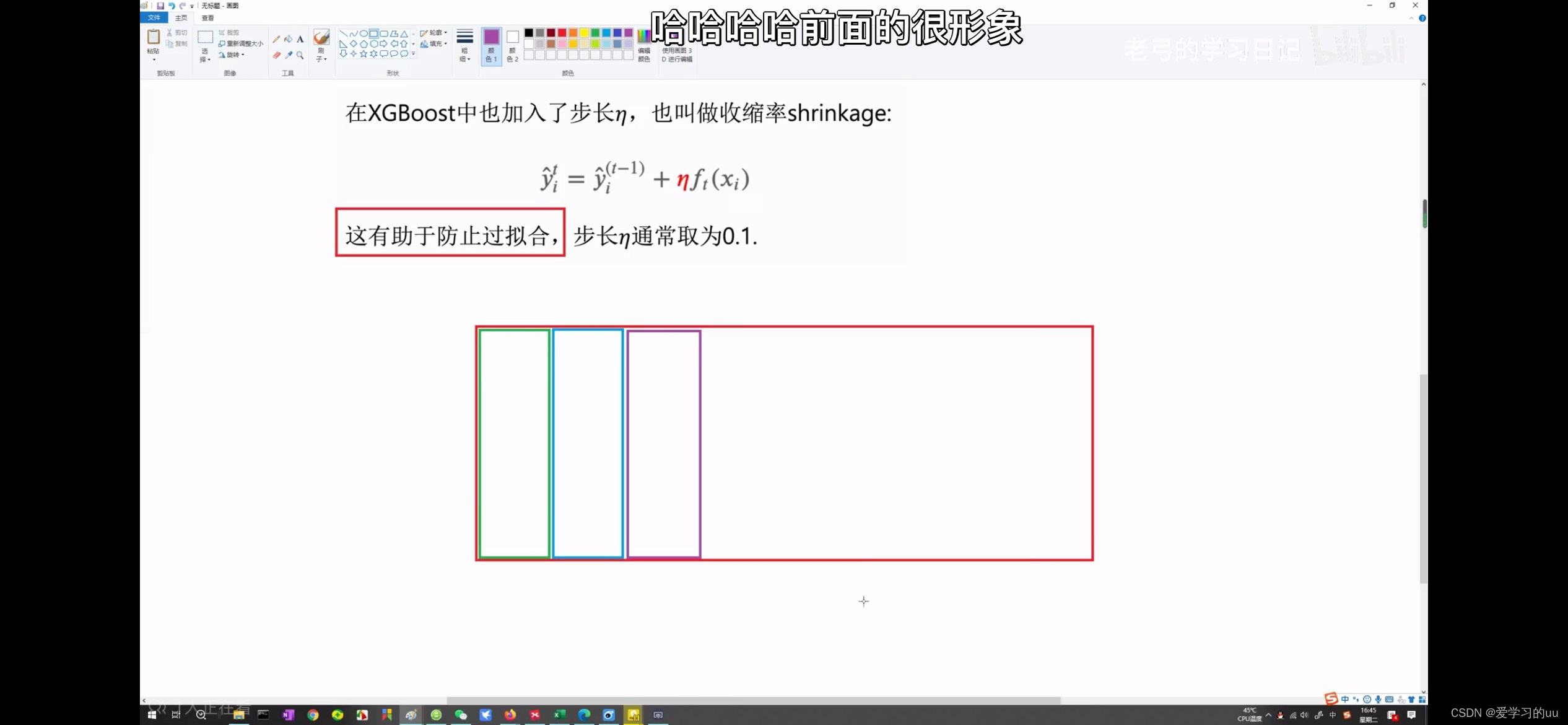
加个学习率让它不要学得太精确,防止过拟合
系统设计
1.核外块运算:
主要有两点,一是把没有一次性读完的数据放在磁盘上,二是单独开个线程,在运算的同时把磁盘的搬到核上,保持运算连贯性
2.分块并行:
解决的问题:
每次树结点分裂都要重新排序
算gain能否并行处理
解决方法:在基学习器学习前就排序,将排序结果保存在block中,按列进行存储。同时保存其索引,通过特征值就可以得到样本值是谁。进而得到gi,hi,得到gain,并把最大的gain筛选出来
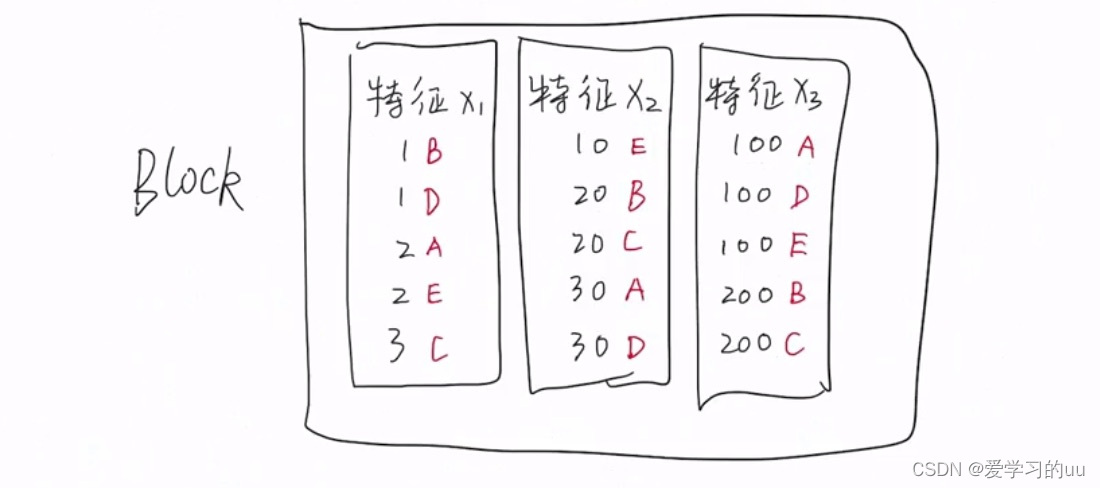
分块计算然后让调度中心判断哪块最大
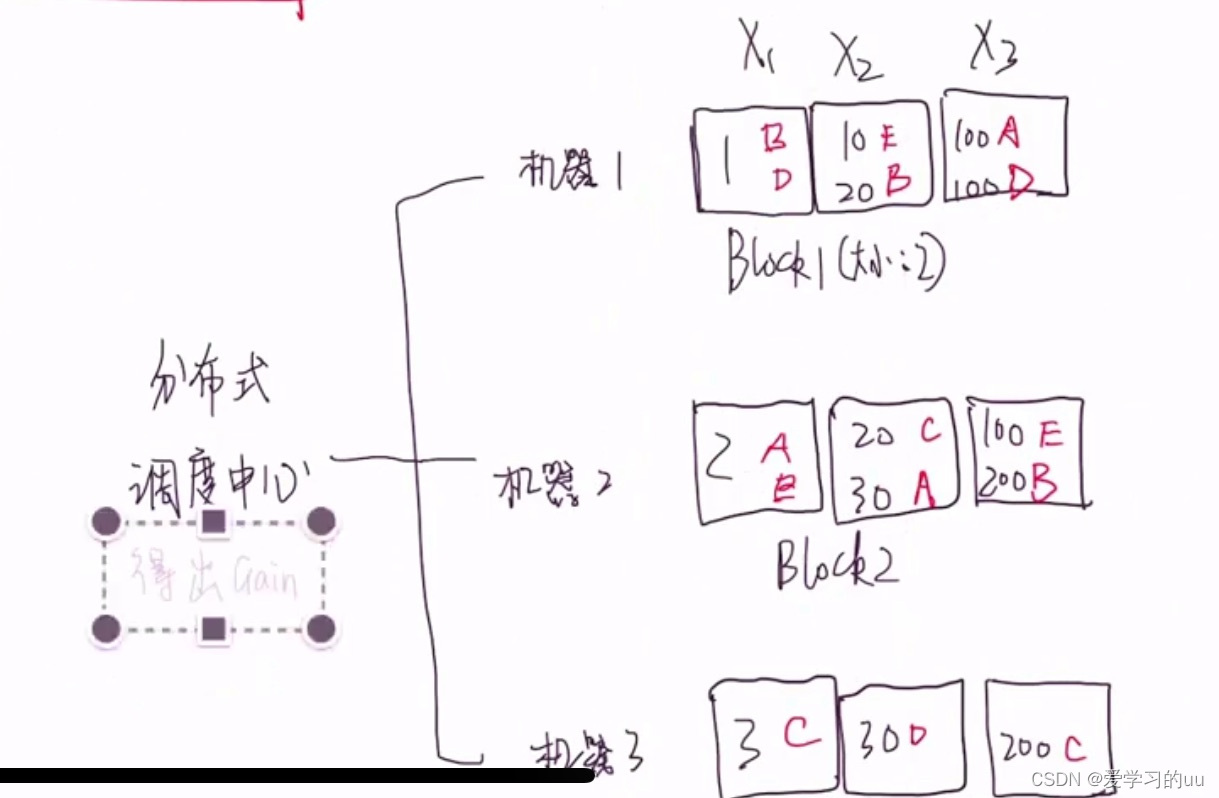
对缓存命中率低这点的优化:
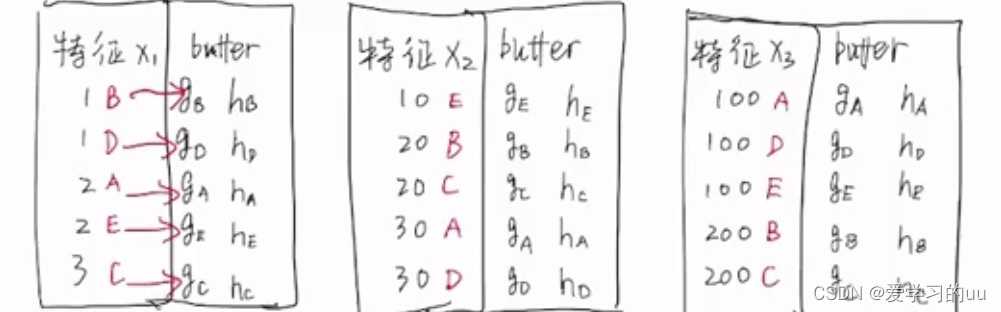
给每个特征值加一个buffer记录记录g和h值