文章目录
- 二项分布
-
- 伯努利试验
- 二项分布
- 泊松近似
- 多项式分布(Multinomial Distribution)
- 负二项分布
- 超几何概率分布
- 矩
- 联合概率密度
-
- 联合概率
- 百度文心一言关于联合概率的解释
- 指数分布概率密度
- 均匀分布
- 高斯混合模型
-
- 正态分布(又名高斯分布)
- 高斯混合分布基本概念
- 百度文心一言关于高斯混合分布的解释:
-
- 定义
- 模型结构
- 参数估计
- 应用领域
- 总结
- 参考文献
二项分布
伯努利试验
- 同样的条件下重复地、相互独立的一种随机试验,只有两种可能结果:发生或者不发生。
- 该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,或称为伯努利概型。
- 事件 Φ \varPhi Φ发生的概率为 p ( 0 < p < 1 ) p(0<p<1) p(0<p<1)
(1) n重伯努利试验中,事件 Φ \varPhi Φ恰好发生 φ \varphi φ 次的概率为:
P n ( φ ) = C n φ p φ ( 1 − p ) n − φ P_n(\varphi)=C_n^{\varphi}p^{\varphi}(1-p)^{n-\varphi} Pn(φ)=Cnφpφ(1−p)n−φ
(2) 事件 Φ \varPhi Φ在第 φ \varphi φ 次试验中才首次发生的概率为:
p ( 1 − p ) φ − 1 p(1-p)^{\varphi-1} p(1−p)φ−1
(3) μ = p , σ 2 = p ( 1 − p ) \mu=p,\sigma^2=p(1-p) μ=p,σ2=p(1−p)
二项分布
- n个独立试验有成功或失败两种结果,单次成功/失败试验又称为伯努利试验,二项分布实质是多次伯努利试验
- 当n=1时,二项分布就是伯努利分布。
- 设每次试验的成功概率 为p。随机变量 Φ \varPhi Φ服从参数为 n 和 p n和p n和p的二项分布。记为: Φ ∽ B ( n , p ) 或 Φ ∽ b ( n , p ) \varPhi\backsim B(n,p)或\varPhi \backsim b(n,p) Φ∽B(n,p)或Φ∽b(n,p)
- μ = n p , σ 2 = n p ( 1 − p ) \mu=np,\sigma^2=np(1-p) μ=np,σ2=np(1−p)
泊松近似
- 当试验的次数趋于无穷大,而乘积np固定时,二项分布收敛于泊松分布。
- 泊松分布属于离散概率分布,适合于描述单位时间内某随机事件发生的次数。
- 某随机事件 Φ \varPhi Φ概率函数为:
p ( Φ = φ ) = λ φ φ ! e − λ p(\varPhi=\varphi)=\frac {\lambda^\varphi} {\varphi!} e ^{-\lambda} p(Φ=φ)=φ!λφe−λ
e 约 为 2.718281828459045 e约为2.718281828459045 e约为2.718281828459045
参数λ是单位时间(或单位面积)内随机事件的平均发生次数。
多项式分布(Multinomial Distribution)
- 多项式分布是二项式分布的推广。
- 具体见二项式分布,百度百科
μ = n p i σ 2 = n p i ( 1 − p i ) \mu=np_i \\\sigma^2=np_i(1-p_i) μ=npiσ2=npi(1−pi)
负二项分布
- 满足以下条件的称为负二项分布:实验包含一系列独立的实验, 每个实验都有成功、失败两种结果,成功的概率是恒定的,实验持续到r次不成功,r为正整数。
- X~NB(r;P)
- 具体见负二项分布,百度百科
μ = r p σ 2 = r q p 2 \mu=\frac r p \\\sigma^2=\frac {rq} {p^2} μ=prσ2=p2rq
超几何概率分布
- 超几何分布是离散概率分布。它描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。
- 超几何分布中的参数是N,n,M,上述超几何分布记作X~H(N,M,n)。
- 具体见超几何分布,百度百科
μ = n M N σ 2 = n ( N − n ) ( N − M ) N 2 ( N − 1 ) \mu=\frac {nM} {N} \\\sigma^2=\frac {n(N-n)(N-M)} {N^2(N-1)} μ=NnMσ2=N2(N−1)n(N−n)(N−M)
矩
- 矩是对变量分布和形态特点的一组度量。
- n阶矩被定义为一变量的n次方与其概率密度函数之积的积分。
- 试图将一个度量μ映射到序列 M n M_n Mn时就产生了矩问题,矩问题指研究概率分布是否被其各阶矩惟一决定的问题。
- n阶矩通常用符号 μ n μ_n μn表示
- 直接使用变量计算的矩被称为原始矩
- 移除均值或期望后计算的矩被称为中心矩
- 变量的一阶原始矩等价于数学期望、二至四阶中心矩被定义为方差、偏度和峰度。
- 原点矩与中心矩
(1)设X是随机变量,若 E ( X k ) ( k = 1 , 2 , . . . ) E(X^k)(k=1,2,...) E(Xk)(k=1,2,...) 存在,则称它为X的k阶原点矩,记作 v k ( X ) v_k(X) vk(X)。
(2)对于正整数k,如果 E ( X ) E(X) E(X)存在,且 E { [ X − E ( X ) ] k } < ∞ E\{[X-E(X)]^k\}<∞ E{[X−E(X)]k}<∞,则称 E { [ X − E ( X ) ] k } E\{[X-E(X)]^k\} E{[X−E(X)]k}为随机变量X的k阶中心矩。 - 具体见矩,百度百科、 矩问题,百度百科,原点矩,百度百科,中心矩,百度百科
联合概率密度
联合概率
-
指在多元的概率分布中多个随机变量分别满足各自条件的概率。
-
假设X和Y都服从正态分布,那么P{X<4,Y<0}就是一个联合概率,表示X<4,Y<0两个条件同时成立的概率。
-
表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P(A∩B)
-
m二项分布的典型例子是扔硬币,硬币正面朝上概率为p, 重复扔n次硬币,k次为正面的概率即为一个二项分布概率。
-
把二项分布公式推广至多种状态,就得到了多项分布。
-
( X 1 = m 1 , X 2 = m 2 , ... , X n = m n ) (X_1=m_1,X_2=m_2,...,X_n=m_n) (X1=m1,X2=m2,...,Xn=mn) 的概率为
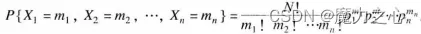
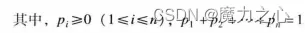
μ i = n p i σ 2 = n p i ( 1 − p i ) \mu_i=np_i \\\sigma^2=np_i(1-p_i) μi=npiσ2=npi(1−pi)
- 更多基础见
联合概率,百度百科
百度文心一言关于联合概率的解释
联合概率密度是描述多个随机变量同时取某一组值的概率的重要工具。以下是关于联合概率密度的详细解释:
-
定义:
- 联合概率密度函数是指多个随机变量同时取某个取值的概率密度函数。假设有两个连续随机变量X和Y,它们的联合概率密度函数为f(x, y)。
-
性质:
- 对于任意的x和y,f(x, y) ≥ 0。
- 对于所有的x和y,联合概率密度函数的积分∫∫f(x, y)dxdy等于1。这符合概率的基本性质。
-
描述随机变量之间的关系:
- 联合概率密度分布可以用来描述多个随机变量之间的依赖关系。
- 如果两个随机变量X和Y是相互独立的,那么它们的联合概率密度函数可以拆分为各自的概率密度函数的乘积,即f(x, y) = f(x) · f(y)。这意味着X和Y之间的取值是相互独立的,一个变量的取值不会对另一个变量的取值产生影响。
- 如果X和Y之间存在依赖关系,那么它们的联合概率密度函数不能拆分为各自的概率密度函数的乘积。
-
计算边际概率密度函数:
- 边际概率密度函数是联合概率密度函数在某个变量上的积分得到的函数。例如,对于随机变量X和Y的联合概率密度函数f(x, y),其边际概率密度函数f(x)表示在给定X的取值下,Y的概率分布。
-
计算条件概率分布:
- 除了边际概率密度函数,我们还可以通过联合概率密度函数计算两个随机变量之间的条件概率分布。条件概率分布描述了在给定某个变量的取值下,另一个变量的概率分布。
- 对于X和Y的联合概率密度函数f(x, y),给定X的取值x,条件概率密度函数f(y|x)表示在已知X的取值为x的条件下,Y的概率密度函数。
-
应用:
- 在实际应用中,联合概率密度分布可以用来对多个随机变量之间的关系进行建模和分析。我们可以根据具体问题选择适当的联合概率密度分布模型,并利用统计方法估计模型参数。
综上所述,联合概率密度是一个强大的工具,可以帮助我们理解和分析多个随机变量之间的复杂关系。
指数分布概率密度
- 连续随机变量X服从参数为λ的指数分布,其中λ>0为常数,记为X~ E(λ),它的概率密度为
f ( x ) = λ e − λ x , x ≥ 0 f ( x ) = 0 , x ≤ 0 f(x)=λe^{-λx},x \ge 0 \\f(x)=0,x \le 0 f(x)=λe−λx,x≥0f(x)=0,x≤0 - 更多见概率统计------4.3 指数分布
均匀分布
- 均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。
- 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为 U ( a , b ) U(a,b) U(a,b)
μ = a + b 2 σ 2 = ( b − a ) 2 12 \mu= \frac {a+b} 2 \\\sigma^2=\frac {(b-a)^2} {12} μ=2a+bσ2=12(b−a)2
- 更多见均匀分布,百度百科
高斯混合模型
正态分布(又名高斯分布)
- 正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,称之为钟形曲线。
- 若随机变量X服从一个数学期望为μ、方差为 σ 2 σ^2 σ2的正态分布,记为 N ∽ ( μ , σ 2 ) N\backsim(μ,σ^2) N∽(μ,σ2)。
- 期望值μ决定了其位置,其标准差σ决定了分布的幅度。
其概率密度函数为
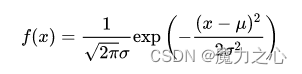
- 标准正态变量
(1) 当μ = 0,σ = 1时的正态分布是标准正态分布。
(2) 数学期望为μ、方差为 σ 2 σ^2 σ2的正态分布通过正态变量标准化公式得到标准正态分布
其公式为
Y = x − μ σ ∽ N ( 0 , 1 ) Y = \frac{x - \mu}{\sigma} \backsim N(0,1) Y=σx−μ∽N(0,1)
其概率密度函数为

- 更多基础见 正态分布,百度百科
高斯混合分布基本概念
- 用高斯概率密度函数(正态分布曲线)精确地量化事物,它是一个将事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。
- 是一种概率分布,它通过将多个高斯分布(正态分布)线性组合来描述一组数据。这种分布模型在机器学习和统计学中非常常见,尤其适用于聚类分析。
- 混合高斯分布的本质在于,它假设数据是由多个子分布(即高斯分布)组成的,每个子分布都有自己的均值和协方差参数,以及一个权重,表示该子分布在整体分布中的贡献程度。
- 混合高斯分布(Gaussian Mixture Model, GMM)在机器学习和统计学中是一种重要的模型,用于描述和模拟数据的分布。
- 更多基础见高斯混合分布,百度百科
百度文心一言关于高斯混合分布的解释:
混合高斯分布(Gaussian Mixture Model, GMM)在机器学习和统计学中是一种重要的模型,用于描述和模拟数据的分布。以下是关于混合高斯分布的详细解释:
定义
混合高斯分布是由多个高斯分布(也称为正态分布)组成的概率分布模型。它假设数据是由这些高斯分布的混合体生成的,其中每个高斯分布被称为一个子模型或组件。混合高斯分布可以表示为这些子模型加权求和的结果。
模型结构
- 子模型:每个子模型都是一个独立的高斯分布,具有自己的均值(mean)、协方差(covariance)和权重(weight)。
- 权重:权重表示每个子模型在混合分布中的重要性或贡献程度,所有子模型的权重之和为1。
参数估计
对于给定的数据集,我们需要通过参数估计的方法来确定混合高斯分布模型中各个子模型的参数。这通常可以通过最大化似然函数或使用期望最大化(Expectation-Maximization, EM)算法来实现。
- 似然函数:似然函数描述了给定数据下模型参数的可能性。在混合高斯分布中,我们需要最大化似然函数以找到最佳的模型参数。
- EM算法:EM算法是一种迭代优化算法,用于在模型参数未知的情况下估计其值。在混合高斯分布中,EM算法通过迭代地估计每个子模型的参数和每个数据点属于各个子模型的概率,从而找到最佳的模型参数。
应用领域
混合高斯分布在多个领域都有广泛的应用,包括但不限于:
- 异常检测:在金融风控和设备状态监测中,混合高斯分布可以用于检测异常数据点。
- 聚类分析:混合高斯分布可以用于将数据点聚类为不同的簇,其中每个簇被视为一个高斯分布的成分。
- 数据分类:通过判断观测数据属于哪个单高斯分布,混合高斯分布可以实现数据的进一步分类。
- 图像分割:在医学图像处理中,混合高斯分布可以用于区分前景和背景,提高图像的识别和区分能力。
- 图像生成:混合高斯分布也可以用于图像生成,通过不同高斯分布的线性组合来拟合任意图像分布。
总结
混合高斯分布是一种强大的概率分布模型,能够描述由多个高斯分布组成的复杂数据。通过合理的参数估计和应用领域的选择,混合高斯分布可以在多个领域发挥重要作用。