强化学习时序差分算法之Q-learning算法——以悬崖漫步环境为例

0.简介

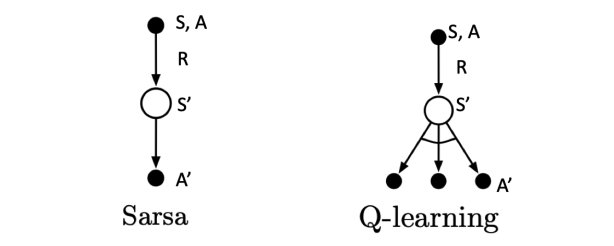
基于时序差分算法的强化学习算法除了Sarsa算法以外还有一种著名算法为Q-learning算法，为离线策略算法，与在线策略算法Sarsa算法相比，其时序差分更新方式变为

Q(St,At)←Q(St,At)+α[Rt+1+γmaxaQ(St+1,a)−Q(St,At)]

对于 Sarsa 来说：

1）在状态 s' 时，就知道了要采取那个动作 a'，并且真的采取了这个动作
2）当前动作 a 和下一个动作 a' 都是根据 ϵ𝜖 -贪婪策略选取的，因此称为on-policy学习

对于 Q-Learning：

1）在状态s'时，只是计算了在 s' 时要采取哪个 a' 可以得到更大的 Q 值，并没有真的采取这个动作 a'。
2）动作 a 的选取是根据当前 Q 网络以及 ϵ𝜖-贪婪策略，即每一步都会根据当前的状况选择一个动作A，目标Q值的计算是根据 Q 值最大的动作 a' 计算得来，因此为 off-policy 学习。

1.导入相关库

python 复制代码

import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm

2.悬崖漫步环境实现环节

python 复制代码

class cliffwalking():
    def __init__(self,colnum,rownum,stepr,cliffr,initx,inity):
        self.colnum=colnum
        self.rownum=rownum
        self.stepr=stepr
        self.cliffr=cliffr
        self.initx=initx
        self.inity=inity
        self.disaster=list(range((self.rownum-1)*self.colnum+1,self.rownum*self.colnum-1))
        self.end=[self.rownum*self.colnum-1]
        self.x=self.initx
        self.y=self.inity
    def step(self,action):
        change=[[0,-1],[0,1],[-1,0],[1,0]]#change[0]上；change[1]下；change[2]左；change[3]右；坐标系原点(0,0)在左上角
        self.x=min(self.colnum-1,max(0,self.x+change[action][0]))
        self.y=min(self.rownum-1,max(0,self.y+change[action][1]))
        nextstate=self.y*self.colnum+self.x
        reward=self.stepr
        done=False
        if nextstate in self.disaster:
            reward=self.cliffr
            done=True
        if nextstate in self.end:
            done=True
        return nextstate,reward,done
    def reset(self):
        self.x=self.initx
        self.y=self.inity
        return self.y*self.colnum+self.x

3.Q-learning算法实现

python 复制代码

class Qlearning():
    """ Qlearning算法 """
    def __init__(self,colnum,rownum,alpha,gamma,epsilon,actionnum=4):
        self.colnum=colnum
        self.rownum=rownum
        self.alpha=alpha#学习率
        self.gamma=gamma#折扣因子
        self.epsilon=epsilon
        self.actionnum=actionnum#动作个数
        self.qtable=np.zeros([self.colnum*self.rownum,self.actionnum])
    def takeaction(self,state):
        if np.random.random()<self.epsilon:
            action=np.random.randint(0,self.actionnum)
        else:
            action=np.argmax(self.qtable[state])
        return action
    def bestaction(self,state):
        qmax=np.max(self.qtable[state])
        a=np.where(self.qtable[state]==qmax)
        return a
    def update(self,s0,a0,r,s1):
        tderror=r+self.gamma*np.max(self.qtable[s1])-self.qtable[s0][a0]
        self.qtable[s0][a0]+=self.alpha*tderror

4.打印目标策略函数

python 复制代码

def printtheagent(agent,env,actionmeaning):
    for i in range(env.rownum):
        for j in range(env.colnum):
            if (i*env.colnum+j) in env.disaster:
                print('****',end=' ')
            elif (i*env.colnum+j) in env.end:
                print('EEEE',end=' ')
            else:
                a=agent.bestaction(i*env.colnum+j)
                b=[0 for _ in range(len(actionmeaning))]
                for m in range(len(actionmeaning)):
                    b[m]=1 if m in a else 0 
                pistr=''
                for k in range(len(actionmeaning)):
                    pistr+=actionmeaning[k] if b[k]>0 else 'o'
                print('%s'%pistr,end=' ')
        print()

5.相关参数设置

python 复制代码

ncol=12#悬崖漫步环境中的网格环境列数
nrow=4#悬崖漫步环境中的网格环境行数
step_reward=-1#每步的即时奖励
cliff_reward=-100#悬崖的即时奖励
init_x=0#智能体在环境中初始位置的横坐标
init_y=nrow-1#智能体在环境中初始位置的纵坐标
alpha=0.1#价值估计更新的步长
epsilon=0.1#epsilon-贪婪算法的探索因子
gamma=0.9#折扣衰减因子
num_episodes=500#智能体在环境中运行的序列总数
tqdm_num=10#进度条的数量
printreturnnum=10#打印回报的数量
actionmeaning=['↑','↓','←','→']#上下左右表示符

6.程序主体部分实现

python 复制代码

np.random.seed(5)
returnlist=[]
env=cliffwalking(colnum=ncol,rownum=nrow,stepr=step_reward,cliffr=cliff_reward,initx=init_x,inity=init_y)
agent=Qlearning(colnum=ncol,rownum=nrow,alpha=alpha,gamma=gamma,epsilon=epsilon,actionnum=4)
for i in range(tqdm_num):
    with tqdm(total=int(num_episodes/tqdm_num)) as pbar:
        for episode in range(int(num_episodes/tqdm_num)):
            episodereturn=0
            state=env.reset()
            done=False
            while not done:
                action=agent.takeaction(state)
                nextstate,reward,done=env.step(action)
                episodereturn+=reward
                agent.update(state,action,reward,nextstate)
                state=nextstate
            returnlist.append(episodereturn)
            if (episode+1)%printreturnnum==0:
                pbar.set_postfix({'episode':'%d'%(num_episodes/tqdm_num*i+episode+1),'return':'%.3f'%(np.mean(returnlist[-printreturnnum:]))})
            pbar.update(1)
episodelist=list(range(len(returnlist)))
plt.plot(episodelist,returnlist)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Qlearning on{}'.format('Cliff Walking'))
plt.show()
print('Qlearning算法最终收敛得到的策略为:')
printtheagent(agent=agent,env=env,actionmeaning=actionmeaning)

7.结果展示

Iteration 0: 100%|████████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 428.50it/s, episode=50, return=-114.000]

Iteration 1: 100%|████████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 895.23it/s, episode=100, return=-72.500]

Iteration 2: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 1222.78it/s, episode=150, return=-66.100]

Iteration 3: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 1519.26it/s, episode=200, return=-40.000]

Iteration 4: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 1533.70it/s, episode=250, return=-26.600]

Iteration 5: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 1925.46it/s, episode=300, return=-38.000]

Iteration 6: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 2387.50it/s, episode=350, return=-47.000]

Iteration 7: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 2949.12it/s, episode=400, return=-25.500]

Iteration 8: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 3133.12it/s, episode=450, return=-34.000]

Iteration 9: 100%|███████████████████████████████████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 3133.44it/s, episode=500, return=-60.400]
Qlearning算法最终收敛得到的策略为:

↑ooo o↓oo ooo→ o↓oo ooo→ ooo→ ooo→ ooo→ o↓oo ooo→ o↓oo o↓oo

o↓oo ooo→ ooo→ ooo→ ooo→ ooo→ o↓oo ooo→ o↓oo ooo→ ooo→ o↓oo

ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ ooo→ o↓oo

↑ooo **** **** **** **** **** **** **** **** **** **** EEEE

8.总结

打印出的回报是行为策略在环境中交互得到的，而不是Q-learning算法在学习的目标策略的真实回报，目标策略打印出来如上所示，发现其更偏向于走在悬崖边上，这与Sarsa算法得到的比较保守的策略相比更优。

比较Sarsa算法与Q-learnig算法在训练中的回报曲线图，可以发现在一个序列中Sarsa算法获得期望回报高于Q-learning算法，原因是训练过程中智能体采取基于当前Q(s,a)函数的-贪婪策略来平衡探索与利用，Q-learning算法由于沿着悬崖边走，会以一定的概率探索"掉入悬崖"这一动作，而Sarsa相对保守的路线使得智能体几乎不可能掉入悬崖。