C++——哈希结构

1.unordered系列关联式容器

本节主要介绍unordered_map和unordered_set两个容器，底层使用哈希实现的

unordered_map

1.unordered_map是储存<key,value>键值对的关联式容器，其允许通过key快速查找到对应的value，和map非常相似，但是底层实现完全不同

2.unoredered_map没有对<key,value>进行排序，而是映射一个对象，其内容与其键相关联，键和映射值的类型可能不同

2.底层结构

unordered系列的关联式容器之所以效率比较高，是因为底层实现了哈希结构

哈希概念

构造一种储存结构，通过某种函数使元素的储存位置与他的关键码建立一一映射的关系，那么在查找该元素的时候很快就能找到

这个顺序表叫做哈希表，但是还有一个问题，如果插入44会出现什么问题？

哈希冲突

不同关键字通过相同的哈希函数计算出相同的哈希地址，这种现象称为哈希冲突

这种情况我们通常用开放定址法和哈希桶解决

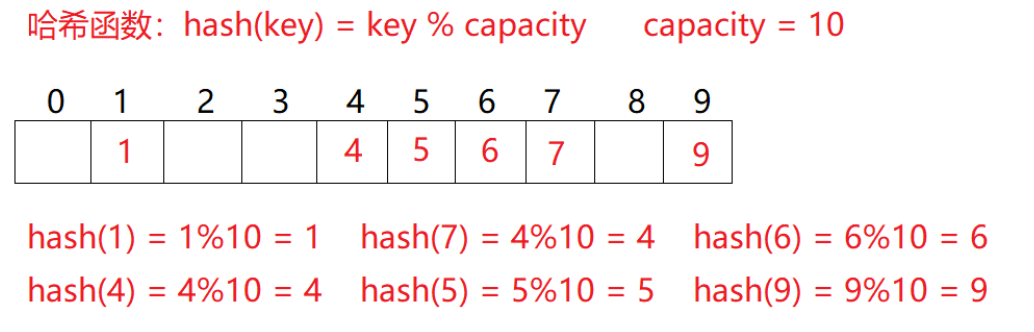
常见哈希函数

常用的除留余数法

就是用我们插入的数据模上哈希表的长度，得出的余数，就是我们得到的插入位置的下标；

哈希表什么时候扩容

开放定址法实现哈希

#pragma once
#include<vector>

template<class K>
struct HashFunc
{
	size_t operator()(const K& key)
	{
		return (size_t)key;
	}
};

//特化
template<>
struct HashFunc<string>
{
	size_t operator()(const string& key)
	{
		size_t hash = 0;
		for (auto ch : key)
		{
			hash *= 131;
			hash += ch;
		}
		return hash;
	}
};

namespace open_address
{
	enum State
	{
		EXIST,
		EMPTY,
		DELETE
	};
	template<class K, class V>
	struct HashData
	{
		pair<K, V> _kv;
		State _state = EMPTY;
	};
	template<class K, class V, class Hash = HashFunc<K>>
	class HashTable
	{
	public:
		HashTable()
		{
			_tables.resize(10);
		}

		bool Insert(const pair<K,V>& kv)
		{
			if (Find(kv.first))
			{
				return false;
			}
			//扩容
			if (_n * 10 / _tables.size() >= 7)
			{
				HashTable<K, V> newHT;
				newHT._tables.resize(_tables.size() * 2);
				for (size_t i = 0; i < _tables.size(); i++)
				{
					if (_tables[i]._state == EXIST)
					{
						newHT.Insert(_tables[i]._kv);
					}
				}
				_tables.swap(newHT._tables);
			}

			Hash hs;
			size_t hashi = hs(kv.first) % _tables.size();

			while (_tables[hashi]._state ==EXIST)
			{
				++hashi;
				hashi %= _tables.size();
			}
			_tables[hashi]._kv = kv;
			_tables[hashi]._state = EXIST;
			++_n;
			return true;
		}
		HashData<K, V>* Find(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();

			while (_tables[hashi]._state != EMPTY)
			{
				if (_tables[hashi]._state == EXIST &&
					_tables[hashi]._kv.first == key)
				{
					return &_tables[hashi];
				}
				++hashi;
				hashi %= _tables.size();
			}
			return nullptr;
		}

		bool Erase(const K& key)
		{
			HashData<K, V>* ret = Find(key);
			if (ret == nullptr)
			{
				return false;
			}
			else
			{
				ret->_state = DELETE;
				--_n;
				return true;
			}
		}

	private:
		vector<HashData<K, V>> _tables;
		size_t _n = 0;
	};