【杂乱笔记】从回溯算法到动态规划

HeaoDng1442024-08-17 11:13

从回溯算法到动态规划

文章目录

回溯

基础定义

回溯（backtracking）被讨论为一种通用的算法技术，用于通过探索所有可能的解决方案来解决问题，并在发现它们无法导致有效的解决方案时立即放弃它们。

具体来说，回溯算法与DFS（深度优先遍历）非常相像

  • 都是通过递归探索所有的解决方案。
  • 时间复杂度均是指数级。

但又有一定的区别：

  • DFS是在遍历【节点】
  • 回溯是在遍历【树枝】

这导致在某些情况下DFS可以转换为回溯，回溯是DFS优化版。

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

解题模板

递归是有解题套路的，可以直接搬到回溯算法里。

1、回溯函数模板返回值以及参数

  • 默认函数名是backtracking ，返回值类型一般先写 void，之后再考虑具体的返回值类型。
  • 再来看一下参数，因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。
cpp 复制代码 
void backtracking(参数)

2、回溯函数的终止条件

  • 一般终止条件是遍历到了【叶子节点】，或是遇到违反题目条件（例如可能会造成cursum>target）一路返回至遍历的起点
cpp 复制代码 
if (终止条件) {
    存放结果;
    return;
}

3、回溯搜索的遍历过程

cpp 复制代码 
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

每一层的递归都有自己需要做的任务，例如力扣第77题. 组合中，每一层递归return之后，我们需要将递归添加进入的path弹出，留给后续递归，这样的好处是每次都由系统帮助我们"擦屁股"。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历 ，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。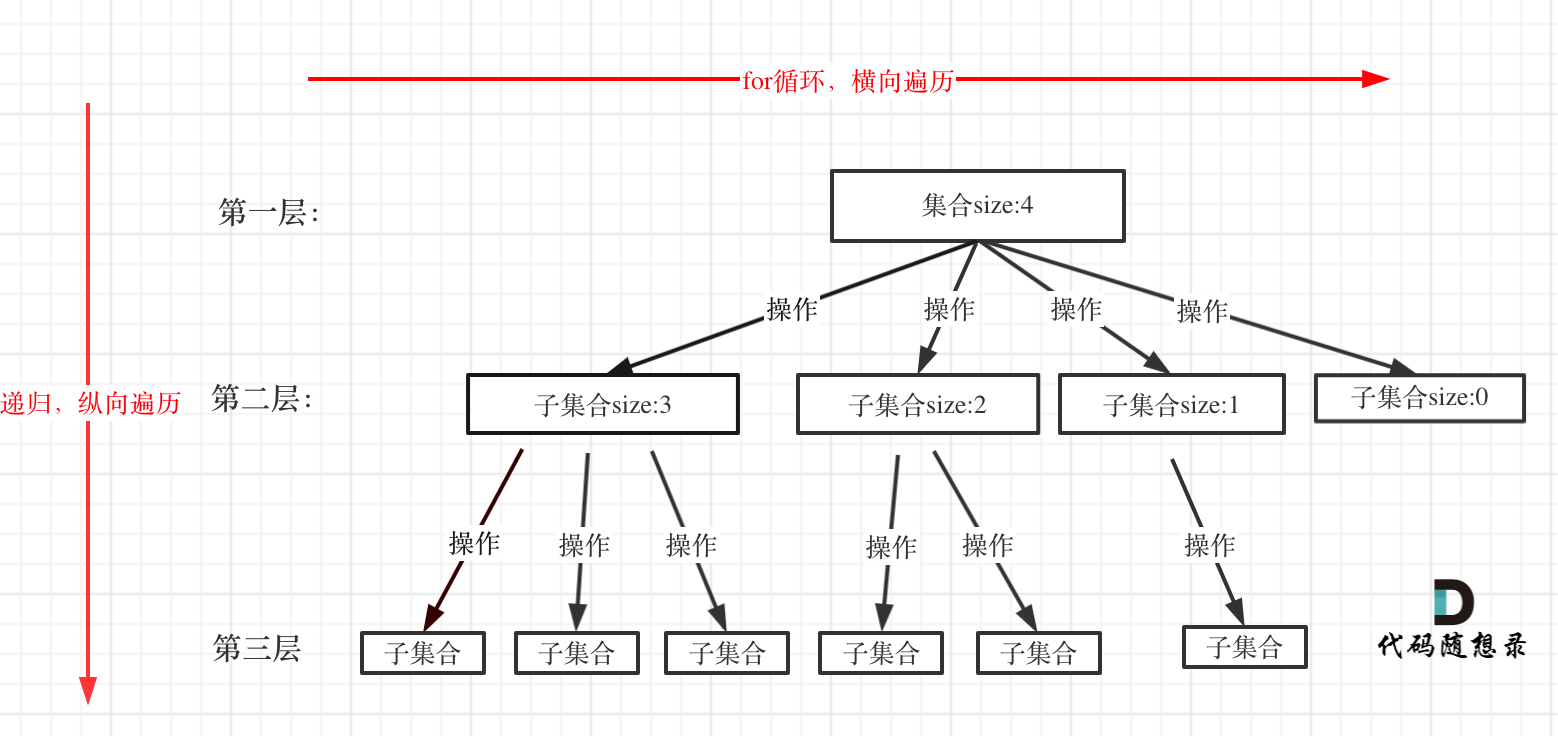

总回溯代码模板如下：

cpp 复制代码 
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

回溯问题分类

一般可以解决如下几种问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

例题分析

组合问题

N个数里面按一定规则找出k个数的集合。

力扣第77题. 组合

代码随想录

cpp 复制代码 
class Solution {
private:
    vector<vector<int>> result; // 存放符合条件结果的集合
    vector<int> path; // 用来存放符合条件结果
    void backtracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= n; i++) {
            path.push_back(i); // 处理节点
            backtracking(n, k, i + 1); // 递归
            path.pop_back(); // 回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear(); // 可以不写
        path.clear();   // 可以不写
        backtracking(n, k, 1);
        return result;
    }
};

[!NOTE]

这里说明了for循环时横向遍历，递归是深度遍历，递归深度就是path的长度。

切割问题

一个字符串按一定规则有几种切割方式

力扣第131题.分割回文串

代码随想录

cpp 复制代码 
class Solution {
private:
    vector<vector<string>> result;
    vector<string> path; // 放已经回文的子串
    void backtracking (const string& s, int startIndex) {
        // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
        if (startIndex >= s.size()) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome(s, startIndex, i)) {   // 是回文子串
                // 获取[startIndex,i]在s中的子串
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {                                // 不是回文，跳过
                continue;
            }
            backtracking(s, i + 1); // 寻找i+1为起始位置的子串
            path.pop_back(); // 回溯过程，弹出本次已经填在的子串
        }
    }
    bool isPalindrome(const string& s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }
};

[!NOTE]

假设输入字符串为 "aab"，我们来看这个算法如何通过回溯找到所有可能的回文分割：

  • Step 1 : 从 startIndex = 0 开始，尝试分割 "a"，判断 "a" 是回文，递归处理剩余部分 "ab"。
  • Step 2 : 在 "ab" 中，尝试分割 "a"，判断 "a" 是回文，继续处理 "b"。
  • Step 3 : 在 "b" 中，判断 "b" 是回文，将其加入路径。此时，路径为 ["a", "a", "b"]，完整分割结束，将其加入 result。
  • Step 4 : 回溯到 "ab" 位置，尝试 "ab"，发现不是回文，跳过。
  • Step 5 : 回溯到初始位置 0，尝试分割 "aa"，判断 "aa" 是回文，递归处理 "b"。
  • Step 6 : 在 "b" 中判断 "b" 是回文，路径为 ["aa", "b"]，将其加入 result。

最后，result 包含两种分割方案：[["a", "a", "b"], ["aa", "b"]]。

子集问题

一个N个数的集合里有多少符合条件的子集

力扣第78题.子集

代码随想录

cpp 复制代码 
class Solution {
public:

    vector<vector<int>> ans;
    vector<int> sub;

    void backtracking(vector<int>& nums,int index)
    {
        ans.push_back(sub);//收集树的所有节点
        for(int i=index;i<nums.size();i++)
        {
            sub.push_back(nums[i]);
            backtracking(nums,i+1);
            sub.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        backtracking(nums,0);
        return ans;
    }
};

[!NOTE]

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

排列问题

N个数按一定规则全排列，有几种排列方式

力扣第46题.全排列

代码随想录

cpp 复制代码 
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;

    void backtracking(vector<int>&nums,vector<bool>&used)
    {
        if(path.size()==nums.size())
        {
            ans.push_back(path);
            return ;
        }

        for (int i = 0; i < nums.size(); i++) {
            if (!used[i]) {
                path.push_back(nums[i]);
                used[i] = true;
                backtracking(nums, used);
                path.pop_back();
                used[i] = false;
            }
        }
    }


    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size()+1,0);
        backtracking(nums,used);
        return ans;
    }
};

[!NOTE]

全排列问题收集的【叶子节点】，并且每次都要从0开始遍历所有元素，所以需要一个used数组来存放是否遍历过这个元素。

棋盘问题

力扣第37题.解数独

代码随想录

cpp 复制代码 
class Solution {
private:
bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {        // 遍历行
        for (int j = 0; j < board[0].size(); j++) { // 遍历列
            if (board[i][j] == '.') {
                for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适
                    if (isValid(i, j, k, board)) {
                        board[i][j] = k;                // 放置k
                        if (backtracking(board)) return true; // 如果找到合适一组立刻返回
                        board[i][j] = '.';              // 回溯，撤销k
                    }
                }
                return false;  // 9个数都试完了，都不行，那么就返回false
            }
        }
    }
    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) { // 判断行里是否重复
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) { // 判断列里是否重复
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

[!NOTE]

解数独独特之处在于它的行列遍历，需要进行两次递归处理。

动态规划

基础定义

回溯算法体现了"决策树"的概念，每个节点代表一个选择点，而路径则代表一个特定的组合。这种结构不仅允许我们系统地探索所有可能性，还通过回溯操作实现了状态的复用，避免了重复的内存分配。更深层次地，每个组合都可以看作是"选择当前元素"和"不选择当前元素"这两个子问题的结果。这种将复杂问题分解为相似但更简单的子问题的方法，不仅是回溯算法的核心，也是许多高效算法的基础思想。

动态规划 （Dynamic Programming，DP）被定义为一种优化技术，它通过将复杂问题分解为一系列更简单的子问题来求解。

区分于回溯算法，动态规划更加注重于强调通过存储和复用子问题的解 来优化问题求解过程，并且某一个状态只能由上一个状态推导出来。（类似于记忆化回溯）

解题模板

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

常见的dp定义及递推公式如下：

动规问题分类

1、背包问题

  • 0-1背包
  • 完全背包
  • 多重背包

2、打家劫舍

3、股票问题

4、子序列问题

  • 连续子序列
  • 不连续子序列
  • 编辑距离
  • 回文

例题分析

背包问题

1、0-1背包

text 复制代码 
每件物品只有一份且具有不同的价值，要放入到一定容量中的背包，请问如何挑选才能保证价值最大。

如果是用回溯算法写出此代码，我们要确保到底是选 还是不选这个物品。

cpp 复制代码 
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Item {
    int weight;
    int value;
};

int maxValue = 0;

void backtrack(vector<Item>& items, int capacity, int currentWeight, int currentValue, int index) {
    // 更新最大价值
    maxValue = max(maxValue, currentValue);

    // 基本情况：如果我们已经考虑了所有物品或背包已满
    if (index == items.size() || currentWeight == capacity) {
        return;
    }

    // 如果还有容量，尝试添加当前物品
    if (currentWeight + items[index].weight <= capacity) {
        backtrack(items, capacity, currentWeight + items[index].weight, 
                  currentValue + items[index].value, index + 1);
    }

    // 不添加当前物品，直接考虑下一个
    backtrack(items, capacity, currentWeight, currentValue, index + 1);
}

int knapsack(vector<Item>& items, int capacity) {
    maxValue = 0;
    backtrack(items, capacity, 0, 0, 0);
    return maxValue;
}

int main() {
    vector<Item> items = {
        {10, 60},
        {20, 100},
        {30, 120}
    };
    int capacity = 50;

    int result = knapsack(items, capacity);
    cout << "背包能够装入的最大价值为: " << result << endl;

    return 0;
}

每次都要考虑是否选择此物品，那么就会最多有2^n个节点（n代表有多少个物品）。树的层数就是背包里物品的数量，且为了找到价值最大的组合，还需要遍历一整棵树才能得到结果。

然而，如果我们仔细观察这个决策树，我们会发现很多子问题是重复的。例如，在不同的决策路径中，我们可能会多次遇到'还剩5kg容量，且还有3个物品可选'这样的情况。

更重要的是，这个问题具有最优子结构的特性。即，如果我们知道了较小容量或较少物品时的最优解，我们就可以利用这些信息来构建更大问题的最优解。

动态规划正是利用了这些特性。它通过将大问题分解为小问题，并存储小问题的解来避免重复计算，从而大大提高了效率。

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, bagweight;// bagweight代表行李箱空间

    cin >> n >> bagweight;

    vector<int> weight(n, 0); // 存储每件物品所占空间
    vector<int> value(n, 0);  // 存储每件物品价值

    for(int i = 0; i < n; ++i) {
        cin >> weight[i];
    }
    for(int j = 0; j < n; ++j) {
        cin >> value[j];
    }
    // dp数组, dp[i][j]代表行李箱空间为j的情况下,从下标为[0, i]的物品里面任意取,能达到的最大价值
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // 初始化, 因为需要用到dp[i - 1]的值
    // j < weight[0]已在上方被初始化为0
    // j >= weight[0]的值就初始化为value[0]
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
        for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
            if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }
    cout << dp[n - 1][bagweight] << endl;

    return 0;
}

空间优化

我们可以看到，dp[i+1] [j+1] 的状态转移只与上一个状态有关，因此我们可以进行空间优化。将二维数组转为一维，相当于数组 dp 滚动存储每一行的值。

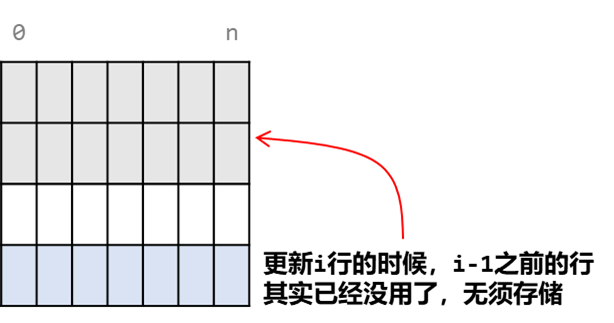
因此我们完全没有必要用一个二维数组存储那么多个状态，而可以使用一个长度为 j + 1 的一维数组重复使用 m 次【m为行数】。

因为我们同时需要左侧，上侧，左上角的数据，势必有数据会被覆盖掉。因此需要一个额外的变量来存储左上角的数据。

cpp 复制代码 
// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;

int main() {
    // 读取 M 和 N
    int M, N;
    cin >> M >> N;

    vector<int> costs(M);
    vector<int> values(M);

    for (int i = 0; i < M; i++) {
        cin >> costs[i];
    }
    for (int j = 0; j < M; j++) {
        cin >> values[j];
    }

    // 创建一个动态规划数组dp，初始值为0
    vector<int> dp(N + 1, 0);

    // 外层循环遍历每个类型的研究材料
    for (int i = 0; i < M; ++i) {
        // 内层循环从 N 空间逐渐减少到当前研究材料所占空间
        for (int j = N; j >= costs[i]; --j) {
            // 考虑当前研究材料选择和不选择的情况，选择最大值
            dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
        }
    }

    // 输出dp[N]，即在给定 N 行李空间可以携带的研究材料最大价值
    cout << dp[N] << endl;

    return 0;
}
2、完全背包

完全背包就是0-1背包的升级版，即物品数量是无限的任取，其实只需要在取的过程中考虑最多能取多少到达最大利润。

回溯算法如下：

cpp 复制代码 
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

struct Item {
    int weight;
    int value;
};

int maxValue = 0;

void backtrack(vector<Item>& items, int capacity, int currentWeight, int currentValue, int index) {
    // 更新最大价值
    maxValue = max(maxValue, currentValue);

    // 基本情况：如果我们已经考虑了所有物品或背包已满
    if (index == items.size() || currentWeight == capacity) {
        return;
    }

    // 尝试添加当前物品多次，直到背包装不下
    for (int count = 0; currentWeight + count * items[index].weight <= capacity; count++) {
        backtrack(items, capacity, 
                  currentWeight + count * items[index].weight, 
                  currentValue + count * items[index].value, 
                  index + 1);
    }
}

int knapsack(vector<Item>& items, int capacity) {
    maxValue = 0;
    backtrack(items, capacity, 0, 0, 0);
    return maxValue;
}

int main() {
    vector<Item> items = {
        {10, 60},
        {20, 100},
        {30, 120}
    };
    int capacity = 50;

    int result = knapsack(items, capacity);
    cout << "背包能够装入的最大价值为: " << result << endl;

    return 0;
}

如果是采用动态规划，时间、空间复杂度会简单很多

cpp 复制代码 
#include <iostream>
#include <vector>
using namespace std;

// 先遍历背包，再遍历物品
void test_CompletePack(vector<int> weight, vector<int> value, int bagWeight) {

    vector<int> dp(bagWeight + 1, 0);

    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        for(int i = 0; i < weight.size(); i++) { // 遍历物品
            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    int N, V;
    cin >> N >> V;
    vector<int> weight;
    vector<int> value;
    for (int i = 0; i < N; i++) {
        int w;
        int v;
        cin >> w >> v;
        weight.push_back(w);
        value.push_back(v);
    }
    test_CompletePack(weight, value, V);
    return 0;
}
3、多重背包

多重背包是在完全背包的基础上多加了个数量限制，多重背包将多余的数量展开成1份也可以视为0-1背包.

cpp 复制代码 
#include<iostream>
#include<vector>
using namespace std;
int main() {
    int bagWeight,n;
    cin >> bagWeight >> n;
    vector<int> weight(n, 0); 
    vector<int> value(n, 0);
    vector<int> nums(n, 0);
    for (int i = 0; i < n; i++) cin >> weight[i];
    for (int i = 0; i < n; i++) cin >> value[i];
    for (int i = 0; i < n; i++) cin >> nums[i];    
    
    for (int i = 0; i < n; i++) {
        while (nums[i] > 1) { // 物品数量不是一的，都展开
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }
 
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品，注意此时的物品数量不是n
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

动态规划：

cpp 复制代码 
#include<iostream>
#include<vector>
using namespace std;
int main() {
    int bagWeight,n;
    cin >> bagWeight >> n;
    vector<int> weight(n, 0);
    vector<int> value(n, 0);
    vector<int> nums(n, 0);
    for (int i = 0; i < n; i++) cin >> weight[i];
    for (int i = 0; i < n; i++) cin >> value[i];
    for (int i = 0; i < n; i++) cin >> nums[i];

    vector<int> dp(bagWeight + 1, 0);

    for(int i = 0; i < n; i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
        }
    }

    cout << dp[bagWeight] << endl;
}

[!CAUTION]

背包问题中的两个for循环至关重要，到底是先遍历物品还是先遍历容量，到底是正序还是逆序，都是需要注意的。

1、0-1背包

  • 0-1背包的滚动数组遍历要求逆序 且先遍历物品后遍历背包容量，因为从状态转移方程中能看到dp[j]中的数据来源于第i-1行的dp[j]和dp[j-W[i]]，正序会导致dp[j-W[i]]提前更新为i行的数据，如果遍历容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。
  • 二维数组dp[i] [j]所需要的数据是左上角，所以是先遍历物品还是先遍历背包均可，但是在先遍历物品后要记得背包的容量应该是从W[i]开始的（非必须但能提高效率）。

2、完全背包

  • 在完全背包的滚动数组中，只要求先遍历物品后遍历背包容量，没有要求逆序。因为在遍历过程中正序会导致同一物体多次放入背包，正好符合完全背包的要求。
打家劫舍

打家劫舍问题也是一个经典的动态规划问题，对比于0-1背包的选或不选，打家劫舍变为了偷或不偷 ，并且约束条件也变为了不能选择相邻元素 ，并且也从价值和容量两个维度变味了房屋序列一维维度。

cpp 复制代码 
#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if (n == 0) return 0;
        if (n == 1) return nums[0];
        
        vector<int> dp(n, 0);
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        
        for (int i = 2; i < n; i++) {
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }
        
        return dp[n-1];
    }
};

int main() {
    Solution solution;
    vector<int> houses = {1, 2, 3, 1};
    cout << "Maximum amount that can be robbed: " << solution.rob(houses) << endl;
    return 0;
}
股票问题

股票问题更像是一种序列决策问题，每一天都需要根据当前状态和未来可能的状态做出决策。

1. 一维状态：maxprofit[i]

  • 状态定义：
    MP[i]：第i天的最大利润，取值[0, n)

  • 状态递推：

    对于股票无非就两种操作，买入和卖出

    • 买入：MP[i] = MP[i - 1] + (-p[i])
    • 卖出：MP[i] = MP[i - 1] + (p[i])

  • 最终状态：
    MP[n - 1]：第n天的最大利润

  • 问题：

    因为只能持有一股，所以买入和卖出的前提分别是未持有和持有，但是只用这一位 i，根本就没法知道是否持有，所以无法正确进行状态递推，所以只用一维不太行...

2. 二维状态：maxprofit[i] [j]

  • 状态定义：
    MP[i][j]：第 i 天未持有股票(j=0)或持有股票(j=1)的最大利润

    • i表示第i天，取值[0, n)
    • j表示当前天是否持有股票，取值为 0或1

  • 状态递推：

    因为是二维状态，所以照理说 i、j 是嵌套循环关系，但由于 j 只有01两种情况，所以直接枚举出来了：

    1. MP[i][0]：我第 i 天没有股票。

      • MP[i][0] = max(MP[i-1][0], MP[i - 1][1] + p[i])
        • MP[i][0] = MP[i-1][0]：我前一天没股票且今天不操作
        • MP[i][0] = MP[i - 1][1] + p[i]：我前一天有股票然后卖出了

    2. MP[i][1]：我第 i 天有股股票。

      • MP[i][1] = max(MP[i-1][1], MP[i - 1][0] - p[i])
        • MP[i][1] = MP[i-1][1]：我前一天持有股票但今天我不操作
        • MP[i][1] = MP[i - 1][0] - p[i]：我前一天没有股票今天买入了

  • 最终状态：
    MP[n-1][0]：i=n-1没什么说的，j=0是因为市场都熄火了，你还持有着股票(j=1)肯定是不值的，就算亏了也要卖掉回点老本

  • 问题一：

    上面说的是交易无限次（122题），那如果是限制只能交易1次（121题）怎么搞？

  • 答：

    可以这么想，如果是允许交易无数次，那么我们在买入股票时的最大利润受前面交易结果的影响，即maxprofit=MP[i-1][0]-p[i]；但如果只能交易一次，我买入了股票就是只用减去花的钱，不考虑之前的状态（MP[i-1][0]），即maxprofit=-p[i]。

    所以，只能交易一次的状态定义不用变，只是在递推时MP[i][1] = max(MP[i-1][1], - p[i])。

3、最多交易k次的情况

  1. 状态定义 :
    • dp[i][j] 表示到第i天结束时，在不同状态j下的最大利润。
    • j的取值范围是 [0, 2k]，其中：
      • 偶数j (0, 2, 4, ...) 表示不持有股票的状态
      • 奇数j (1, 3, 5, ...) 表示持有股票的状态
  2. 初始化 :
    • 对于第0天，所有持有股票的状态（奇数j）初始化为 -prices[0]
    • 不持有股票的状态（偶数j）初始化为0
  3. 状态转移 :
    • 对于持有股票的状态 (j为奇数): dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i])
    • 对于不持有股票的状态 (j为偶数): dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + prices[i])
  4. 最终结果 : 最大利润为 dp[prices.size()-1][2k]，即最后一天完成k次交易后不持有股票的状态。
子序列问题
1、连续子序列

**连续子序列（子数组）问题 **

连续子序列问题通常更简单，因为我们只需要考虑当前元素和前一个元素的关系。

  • 典型问题：最大子数组和

    • 状态定义： dp[i] 表示以第 i 个元素结尾的最大子数组和

    • 状态转移方程： dp[i] = max(nums[i], dp[i-1] + nums[i])

    cpp 复制代码 
    int maxSubArray(vector<int>& nums) {
    int n = nums.size();
    vector<int> dp(n);
    dp[0] = nums[0];
    int maxSum = dp[0];
    
    for (int i = 1; i < n; i++) {
        dp[i] = max(nums[i], dp[i-1] + nums[i]);
        maxSum = max(maxSum, dp[i]);
    }
    
    return maxSum;
}

2、不连续子序列

不连续子序列问题通常更复杂，因为我们需要考虑包含或不包含当前元素的情况。

  • 典型问题：最长递增子序列（LIS）

    • 状态定义： dp[i] 表示以第 i 个元素结尾的最长递增子序列的长度

    • 状态转移方程： dp[i] = max(dp[j] + 1) for j in [0, i) if nums[j] < nums[i]

    cpp 复制代码 
    int lengthOfLIS(vector<int>& nums) {
    int n = nums.size();
    vector<int> dp(n, 1);
    int maxLen = 1;
    
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
        maxLen = max(maxLen, dp[i]);
    }
    
    return maxLen;
}
连续子序列与非连续子序列关键区别
  1. 状态定义 ：
    • 连续：通常只需考虑以当前元素结尾的情况
    • 不连续：可能需要考虑更多的前置状态
  2. 状态转移 ：
    • 连续：通常只与前一个状态有关
    • 不连续：可能需要考虑之前的所有状态
  3. 复杂度 ：
    • 连续：通常可以在 O(n) 时间内解决
    • 不连续：通常需要 O(n^2) 或更高的时间复杂度
3、编辑距离

编辑距离问题是一个经典的动态规划问题，用于计算将一个字符串转换成另一个字符串所需的最少操作次数。

  • 状态定义： dp[i][j] 表示将 word1 的前 i 个字符转换成 word2 的前 j 个字符所需的最少操作次数。

  • 状态转移方程：

    • 如果 word1[i-1] == word2[j-1]： dp[i][j] = dp[i-1][j-1]

    • 否则：

      dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
      • dp[i-1] [j] + 1：删除操作
      • dp[i] [j-1] + 1：插入操作
      • dp[i-1] [j-1] + 1：替换操作

  • cpp

    cpp 复制代码 
    class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.length(), n = word2.length();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        
        for (int i = 0; i <= m; i++) dp[i][0] = i;
        for (int j = 0; j <= n; j++) dp[0][j] = j;
        
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1[i-1] == word2[j-1]) {
                    dp[i][j] = dp[i-1][j-1];
                } else {
                    dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;
                }
            }
        }
        
        return dp[m][n];
    }
};
4、回文

1. 最长回文子序列

最长回文子序列（Longest Palindromic Subsequence, LPS）

这个问题要求在给定字符串中找出最长的回文子序列（可以不连续）。

  • 状态定义： dp[i][j] 表示字符串从索引 i 到 j 的子串中，最长回文子序列的长度。

  • 状态转移方程：

    • 如果 s[i] == s[j]： dp[i][j] = dp[i+1][j-1] + 2
    • 否则： dp[i][j] = max(dp[i+1][j], dp[i][j-1])

  • cpp

    cpp 复制代码 
    class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.length();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        
        // 初始化长度为1的回文子序列
        for (int i = 0; i < n; i++) {
            dp[i][i] = 1;
        }
        
        // 填充dp表
        for (int len = 2; len <= n; len++) {
            for (int i = 0; i < n - len + 1; i++) {
                int j = i + len - 1;
                if (s[i] == s[j] && len == 2) {
                    dp[i][j] = 2;
                } else if (s[i] == s[j]) {
                    dp[i][j] = dp[i+1][j-1] + 2;
                } else {
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        
        return dp[0][n-1];
    }
};

2. 最长回文子串

最长回文子串（Longest Palindromic Substring）

这个问题要求在给定字符串中找出最长的回文子串（必须连续）。

  • 状态定义： dp[i][j] 表示字符串从索引 i 到 j 的子串是否为回文串。

  • 状态转移方程：

    • 如果 s[i] == s[j]： dp[i][j] = dp[i+1][j-1]（当 j - i > 2 时）
    • 否则： dp[i][j] = false

  • cpp

    cpp 复制代码 
    class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.length();
        vector<vector<bool>> dp(n, vector<bool>(n, false));
        int start = 0, maxLen = 1;
        
        // 所有长度为1的子串都是回文
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        
        // 检查长度为2的子串
        for (int i = 0; i < n - 1; i++) {
            if (s[i] == s[i+1]) {
                dp[i][i+1] = true;
                start = i;
                maxLen = 2;
            }
        }
        
        // 检查长度大于2的子串
        for (int len = 3; len <= n; len++) {
            for (int i = 0; i < n - len + 1; i++) {
                int j = i + len - 1;
                if (s[i] == s[j] && dp[i+1][j-1]) {
                    dp[i][j] = true;
                    if (len > maxLen) {
                        start = i;
                        maxLen = len;
                    }
                }
            }
        }
        
        return s.substr(start, maxLen);
    }
};
相关推荐
დ旧言~6 分钟前
专题八：背包问题
算法·leetcode·动态规划·推荐算法
_WndProc24 分钟前
C++ 日志输出
开发语言·c++·算法
努力学习编程的伍大侠37 分钟前
基础排序算法
数据结构·c++·算法
车轮滚滚__37 分钟前
uniapp对接unipush 1.0 ios/android
笔记
林辞忧39 分钟前
动态规划＜四＞ 回文串问题(含对应LeetcodeOJ题)
动态规划
XiaoLeisj1 小时前
【递归，搜索与回溯算法 & 综合练习】深入理解暴搜决策树：递归，搜索与回溯算法综合小专题（二）
数据结构·算法·leetcode·决策树·深度优先·剪枝
Jasmine_llq1 小时前
《 火星人 》
算法·青少年编程·c#
闻缺陷则喜何志丹2 小时前
【C++动态规划 图论】3243. 新增道路查询后的最短距离 I|1567
c++·算法·动态规划·力扣·图论·最短路·路径
Lenyiin2 小时前
01.02、判定是否互为字符重排
算法·leetcode
热门推荐
01〔AI 绘画〕Stable Diffusion 之 解决绘制多人或面部很小的人物时面部崩坏问题 篇02ARM学习（31）编译器对overlay方式的支持03玄机平台应急响应—webshell查杀04DisplayPort AltMode On Type-c协议_Ver2.0(学习笔记)05校验 GPT-4 真实性的三个经典问题：快速区分 GPT-3.5 与 GPT-4，并提供免费测试网站06Docker 夺命连环 15 问076个主流的工业3D管道设计软件08基于大语言模型（LLM）的合成数据生成、策展和评估的综述09(欧拉)openEuler系统添加网卡文件配置流程、(欧拉)openEuler系统手动配置ipv6地址流程、(欧拉)openEuler系统网络管理说明10红米手机使用google play