目录
tags
组合数 二叉搜索树
中文题面
定义一棵二叉搜索树满足,点有点权,左儿子的点权 ≤ \leq ≤ 根节点的点权,右儿子的点权 ≥ \geq ≥ 根节点的点权。
现在给定一棵 n n n 个点二叉搜索树的形态与一些点的权值;问有多少种填剩余点的点权的方法,使得所有点的点权都 ∈ [ 1 , C ] \in[1,C] ∈[1,C]。
输入格式
每个测试由多个测试用例组成。第一行包含一个整数 t t t ( 1 ≤ t ≤ 1 0 5 1 \le t \le 10^5 1≤t≤105 )------测试用例的数量。下面是测试用例的描述。
每个测试用例的第一行包含两个整数 n n n 和 C C C ( 2 ≤ n ≤ 5 ⋅ 1 0 5 2 \leq n \leq 5 \cdot 10^5 2≤n≤5⋅105 , 1 ≤ C ≤ 1 0 9 1 \leq C \leq 10^9 1≤C≤109 )------树中的顶点数和顶点上允许的最大值。
接下来的 n n n 行描述了树的顶点。 i i i 行包含三个整数 L i , R i L_i, R_i Li,Ri 和 v a l i val_i vali ( − 1 ≤ L i , R i ≤ n -1 \le L_i, R_i \le n −1≤Li,Ri≤n , − 1 ≤ v a l i ≤ C -1 \le val_i \le C −1≤vali≤C , L i , R i , v a l i ≠ 0 L_i, R_i, val_i \ne 0 Li,Ri,vali=0 )------分别是左子节点的个数、右子节点的个数和 i i i 顶点处的值。如果是 L i = − 1 L_i = -1 Li=−1,那么 i i i 顶点没有左子顶点。如果是 R i = − 1 R_i = -1 Ri=−1,那么 i 顶点没有右子。如果是 v a l i = − 1 val_i = -1 vali=−1,那么第 i i i 顶点处的值是未知的。
保证至少存在一棵合适的二叉搜索树。
可以保证所有测试用例 n n n 的总和不超过 5 ⋅ 1 0 5 5 \cdot 10^5 5⋅105。
输出格式
对于每个测试用例,输出一个整数------合适的二叉搜索树的个数对 998244353 998244353 998244353 取模。
样例输入
3
5 5
2 3 -1
-1 -1 2
4 -1 3
-1 5 -1
-1 -1 -1
3 69
2 3 47
-1 -1 13
-1 -1 69
3 3
2 3 -1
-1 -1 -1
-1 -1 -1样例输出
4
1
10说明
在第一个测试用例中,二叉搜索树具有以下形式:
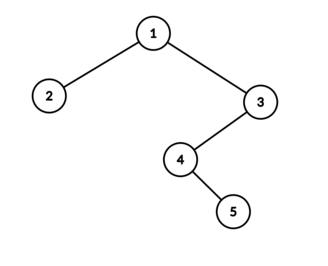
那么在顶点的可能值是: [ 2 , 2 , 3 , 2 , 2 ] [2,2,3,2,2] [2,2,3,2,2], [ 2 , 2 , 3 , 2 , 3 ] [2,2,3,2,3] [2,2,3,2,3], [ 2 , 2 , 3 , 3 , 3 ] [2,2,3,3,3] [2,2,3,3,3], [ 3 , 2 , 2 , 3 , 3 ] [3,2,2,3,3] [3,2,2,3,3], [ 3 , 2 , 2 , 3 , 3 ] [3,2,2,3,3] [3,2,2,3,3], [ 3 , 2 , 2 , 3 , 3 ] [3,2,2,3,3] [3,2,2,3,3]。
在第二个测试用例中,所有顶点的值都是已知的,因此只有一个合适的二叉搜索树。
思路
首先我们可以想到二叉搜索树的性质:中序遍历整个二叉搜索树得到它的序列,这个序列是不减的,即对于 1 ≤ i ≤ j ≤ n 1\le i \le j \le n 1≤i≤j≤n 有 a i ≤ a j a_i\le a_j ai≤aj,接下来我们只需要填充无值的点(即 v a l = − 1 val=-1 val=−1)即可。
举个例子,比如在样例一中中序遍历得到 [ 2 , − 1 , − 1 , − 1 , 3 ] [2,-1,-1,-1,3] [2,−1,−1,−1,3],那么 a 2 , a 3 , a 4 a_2,a_3,a_4 a2,a3,a4 需要填值,值域为 [ m a x ( 1 , a 1 ) , m i n ( C , a 5 ) ] = [ 2 , 3 ] [max(1, a_1), min(C,a_5)]=[2,3] [max(1,a1),min(C,a5)]=[2,3]。
事实上这是个经典组合数问题,设值域为 [ l , r ] [l, r] [l,r],待填位置有 x x x 个,那么 填数方案数 = C ( r − l + x , x ) \text{填数方案数}=C(r-l+x, x) 填数方案数=C(r−l+x,x),用暴力算组合数即可解决,因为
- C ( n , x ) = n ! ( n − x ) ! x ! = ∏ n − x + 1 n i x ! C(n, x)=\frac{n!}{(n-x)!x!}=\frac{∏_{n-x+1}^ni}{x!} C(n,x)=(n−x)!x!n!=x!∏n−x+1ni
发现实际上暴力算组合数能够在 O ( x ) O(x) O(x) 的时间复杂度内解决,而本题限制了 ∑ n ≤ 5 × 1 0 5 ∑ n \le 5\times10^5 ∑n≤5×105, x x x 最多取到 n n n,不会超时。
代码
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N (int)5e5 + 5
#define pdd pair<double, double>
#define pii pair<int, int>
#define l first
#define r second
int a, b, c, d, x, y, n, m, t, k, q, z, h;
int v[N], rd[N];
int p[N];
pii g[N];
const int mod = 998244353;
const int mmd = 114514;
vector<int> G;
string s;
map<int, int> mp;
void dfs(int now) {
if (g[now].l!=-1) dfs(g[now].l);
G.push_back(v[now]);
if (g[now].r!=-1) dfs(g[now].r);
}
int qpow(int a, int b) {
a %= mod;
int ans = 1;
for (; b; b>>=1) {
if (b & 1) ans *= a, ans%=mod;
a *= a, a%=mod;
}
return ans;
}
int C(int n, int m) {
// n!/(n-m)!m!
int zi = 1;
for (int i = n; i > n - m; i--) zi *= i, zi %= mod;
return zi * qpow(p[m], mod-2) % mod;
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
p[0] = p[1] = 1;
for (int i = 2; i <= 5e5; i++) p[i] = p[i - 1] * i, p[i] %= mod;
cin >> t;
while (t--) {
cin >> n >> c;
G.clear();
for (int i = 1; i <= n; i++) rd[i] = 0, g[i].l = g[i].r = -1, v[i] = -1;
for (int i = 1; i <= n; i++) {
cin >> g[i].l >> g[i].r >> v[i];
if (g[i].l!=-1) rd[g[i].l]++;
if (g[i].r!=-1) rd[g[i].r]++;
}
for (int i = 1; i <= n; i++) {
if (rd[i]==0) {
dfs(i);
break;
}
}
int res = 1;
for (int i = 0; i < G.size(); i++) {
if (G[i] == -1) {
int ll = i;
int rr = 0;
int kua = -1;
for (int j = i + 1; j < G.size(); j++) {
if (G[j] != -1) {
kua = G[j] - (i - 1 >= 0 ? G[i - 1] : 1);
rr = j;
i = j;
break;
}
}
if (kua == -1) {
rr = G.size();
kua = c - (i - 1 >= 0 ? G[i - 1] : 1);
i = G.size();
}
res *= C(rr-ll+kua, rr-ll);
res %= mod;
}
}
cout << res << '\n';
}
return 0;
}