力扣第六十一题——旋转链表

内容介绍

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k个位置。

示例 1：
复制代码
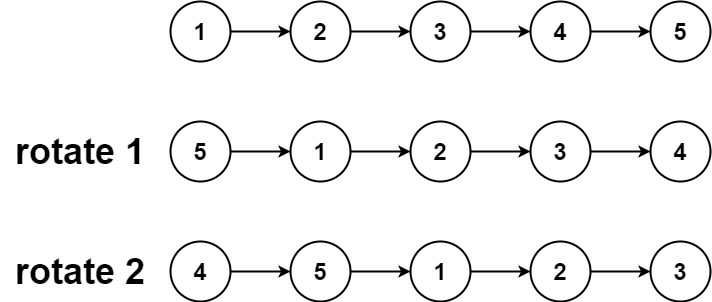
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]
示例 2：
复制代码
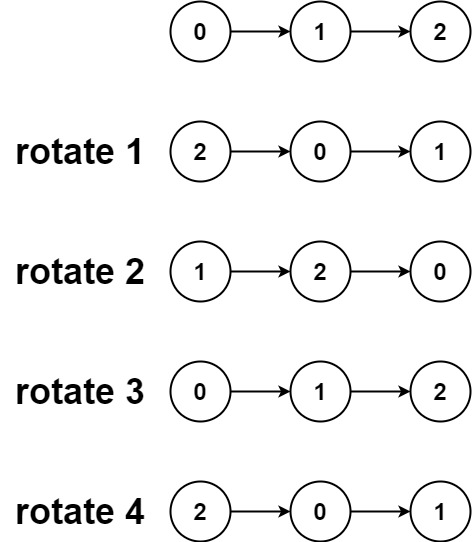
输入：head = [0,1,2], k = 4
输出：[2,0,1]
提示：

链表中节点的数目在范围 [0, 500] 内

-100 <= Node.val <= 100

0 <= k <= 2 * 109

完整代码

 struct ListNode* rotateRight(struct ListNode* head, int k) {
    if (k == 0 || head == NULL || head->next == NULL) {
        return head;
    }
    int n = 1;
    struct ListNode* iter = head;
    while (iter->next != NULL) {
        iter = iter->next;
        n++;
    }
    int add = n - k % n;
    if (add == n) {
        return head;
    }
    iter->next = head;
    while (add--) {
        iter = iter->next;
    }
    struct ListNode* ret = iter->next;
    iter->next = NULL;
    return ret;
}

思路详解

代码功能

这段代码定义了一个名为rotateRight的函数，它接受一个链表的头节点head和一个整数k，然后执行链表的右旋转操作。右旋转意味着将链表的每个元素向右移动k个位置，链表的末尾元素将移动到链表的头部。

思路详解

边界条件检查
- 如果k等于0，或者链表为空head == NULL，或者链表只有一个节点head->next == NULL，则不需要旋转，直接返回head。
计算链表长度
- 使用变量n来计算链表的长度。通过遍历整个链表，每访问一个节点，n的值增加1。
确定旋转次数
- 由于旋转n次链表会回到原状，所以使用k % n来计算实际需要旋转的次数。
- 计算需要移动到链表尾部的节点数add，即n - k % n。
连接链表首尾
- 将链表的最后一个节点（iter）的next指针指向链表的头节点head，形成一个环。
找到新的链表尾部
- 通过遍历add次，找到新的链表尾部。这个位置将是新的头节点的前一个节点。
断开链表
- 将新的尾部节点的next指针设置为NULL，从而断开环，形成新的链表。
返回新的头节点
- ret指向新的头节点，即原链表的第add + 1个节点，返回ret作为旋转后的链表头。

总结

这段代码通过以下步骤实现了链表的右旋转：

计算链表长度。
计算实际旋转次数。
将链表首尾相连形成环。
找到新的链表尾部，并断开环。
返回新的头节点。

知识点精炼

链表基础

链表是一种常见的数据结构，由节点组成，每个节点包含数据和指向下一个节点的指针。

2. 旋转操作

链表旋转是指将链表中的节点按照指定的次数向右或向左移动。

3. 边界条件

检查链表是否为空、链表长度是否为1或旋转次数是否为0，以确定是否需要执行旋转。

4. 计算链表长度

通过遍历链表来计算其长度，为后续旋转操作做准备。

5. 实际旋转次数

使用取模运算k % n来确定实际需要旋转的次数，以避免不必要的完整旋转。

6. 形成环

将链表的最后一个节点的next指针指向头节点，形成环状结构。

7. 寻找新的尾部

通过遍历确定新的尾部位置，以便断开环。

8. 断开环

将新的尾部节点的next指针设置为NULL，完成旋转操作。

9. 返回新头节点

返回旋转后的新头节点，完成链表的右旋转。

10. 算法效率

时间复杂度：O(n)，空间复杂度：O(1)，实现高效链表旋转。

拓展：下次旋转的次数

旋转次数的计算

假设链表长度为 n，给定的旋转次数为 k。旋转链表 k 次意味着每个节点向右移动 k 个位置。

由于链表是一个循环结构，旋转 n 次实际上会使链表回到原始状态。因此，如果 k 大于或等于 n，我们只需要旋转 k % n 次，因为额外的旋转不会改变链表的结构。

计算过程

计算链表长度 n：

int n = 1;
struct ListNode* iter = head;
while (iter->next != NULL) {
    iter = iter->next;
    n++;
}

这段代码通过遍历链表来计算链表的长度 n。

计算实际旋转次数：
```
int add = n - k % n;
```
这行代码计算了实际需要旋转的次数。这里 k % n 是 k 除以 n 的余数，表示 k 相对于 n 的额外旋转次数。由于我们是从链表尾部开始旋转，所以实际需要向右移动的次数是 n - (k % n)。

示例

假设链表长度 n 为 5，旋转次数 k 为 7：

k % n = 7 % 5 = 2
实际旋转次数 add = n - k % n = 5 - 2 = 3

这意味着我们需要将链表向右旋转 3 次。

结论

通过计算 n - k % n，我们得到了实际需要旋转的次数，这个值告诉我们在哪里断开链表，以形成新的头节点。如果 add 等于 n，则不需要旋转，链表保持不变。如果不是，我们就知道需要旋转 add 次，并且新的头节点将是原链表的第 add + 1 个节点。