Unity Shader实现简单的各向异性渲染（采用各向异性形式的GGX分布）

最近刚结束GAMES202的学习，准备慢慢过渡到GAMES103。GAMES103的作业框架为Unity，并没有接触过，因此准备先学一点Unity的使用。刚好101和202都是渲染相关的，因此先学习使用Unity的Shader。

Unity的Shader采用了HLSL，与GLSL不同的地方挺多（写过202的作业，对GLSL印象不怎么好）。最喜欢的地方就是对于材质，它有一个面板，新建一个材质属性，可以自己方便地调节参数，不用在代码里修改。而GLSL想要使用和调节新的参数，还需要在Shader外部作修改。

在101的作业7中，有一个附加项是自己实现Mircofacet模型，但是当时是刚接触PBR渲染不久，仅仅使用了简单的各向同性的微表面。因此这次写一次各向异性的材质来填一填前面的坑，同时适应以下Unity的Shader部分与通常操作。

准备工作

要实现这个效果，需要先确定BRDF部分。

BRDF部分

以下为通常我们所见到的Mircofacet模型的BRDF

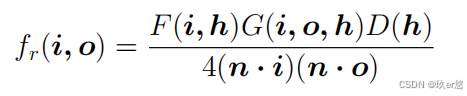
BRDF的效果取决于位于分子的三个部分。采用各向异性的形式，上面的三个部分该如何变化呢？

菲涅尔项F，取决于材质本身的属性，不受到表面状态的变化。比如一块铁，无论如何加工其表面，其菲涅尔项都不会发生变化。这里的我的实现采用了Schlick近似的方法来获取菲涅先项。很显然在公式中，菲涅尔项仅和折射率有关，和表面粗糙度无关。

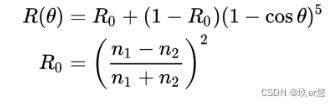
法线分布函数D，这里采用各向异性形式的GGX分布函数。

下图为GGX分布函数的各向同性形式和各向异性形式

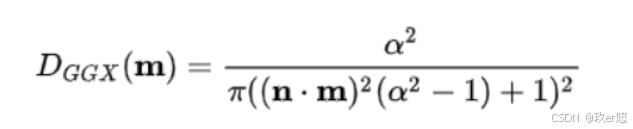
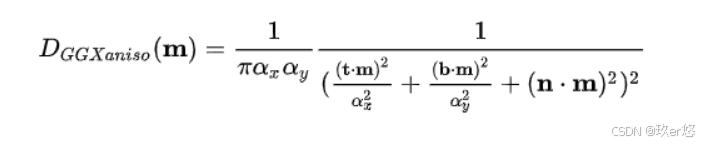
其中，t是切线，b是副切线，n是宏观法线，m是微观法线。αx是切线方向粗糙度，αy是副切线方向粗糙度。

几何遮蔽函数G，这里采用了GGX模型对应的Smith遮蔽项。采用了各项异性的形式。

Smith遮蔽项的通常形式。对于具有形状不变性的NDF，可以求出其Λ函数的解析式。因此得到Λ解析式后，代入该式子就可以求出一个方向的几何遮蔽。对于出射光和入射光分别求一次并将结果相乘就是最后的几何遮蔽项。

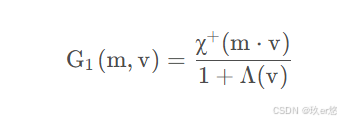
下面是各向同性的GGX对应的Smith遮蔽的Λ解析式

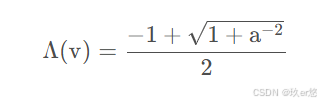
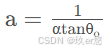
在各向异性的情况下，α使用如下的α0。具体的推导过程，可以看文章最后的参考。

这里的θ和Φ都是将入射光方向转为球面坐标后的角度。再将其代入推到成向量的形式，可以得到最后的G1式子

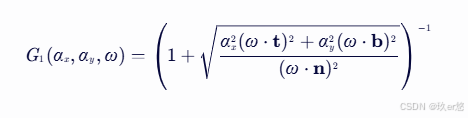
Unity部分

通过了上面的分析，对于着色点的着色需要以下步骤

1.获取法线，切线，副切线

2.获取视线方向和光线方向

3.通过视线方向与光线方向，求得半程向量来代替微观法线方向

4.通过上面的数据，求得F,G,D项

5.在贴图上获取着色点的原始色

6.代入渲染方程完成颜色的计算

对于切线的获取，Unity已经帮我们封装好了功能，不需要再通过uv坐标和点坐标来获取切线了。而副切线只需要法向量叉乘以下切线就可以得到。

代码

cpp 复制代码

Shader "Unlit/My test Shader"
{
    Properties
    {
        _MainTex ("Texture", 2D) = "white" {}
        _RoughnessX ("RoughnessX" , Range (0.0 , 1.0)) = 0.5
        _RoughnessY ("RoughnessY" , Range (0.0 , 1.0)) = 0.5
        _IOR ("IOR" , Range (1.0,30.0)) = 1.5
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        LOD 100

        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag
            // make fog work
            #pragma multi_compile_fog

            #define PI 3.14159265358979323846f

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
                float4 normal : NORMAL;
                float4 tangent : TANGENT;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float3 worldNormal : TEXCOORD1;
                float3 worldPos : TEXCOORD2;
                float3 worldTangent : TEXCOORD3;
                float3 worldBiTangent : TEXCOORD4;
                UNITY_FOG_COORDS(1)
                float4 vertex : SV_POSITION;
            };

            sampler2D _MainTex;
            float4 _MainTex_ST;
            float _IOR;
            float _RoughnessX;
            float _RoughnessY;

            //菲涅尔项
            float fresnel(float3 I,float3 N,float IOR1,float IOR2){
                float R0 = pow( (IOR1-IOR2) / (IOR1 + IOR2) , 2 );
                float cos_theta = dot(I,N);
                return R0 + (1-R0)*pow(1-cos_theta,5);
            }

            //各向异性的GGX函数，这里直接搬了UE4的代码实现
            float DistributionGGX_Aniso( float ax, float ay, float NoH, float3 H, float3 X, float3 Y )
            {
                float XoH = dot( X, H );
                float YoH = dot( Y, H );
                float d = XoH*XoH / (ax*ax) + YoH*YoH / (ay*ay) + NoH*NoH;
                return 1 / ( PI * ax*ay * d*d );
            }
            //G1
            float smithG_GGX_aniso(float dotVN, float dotVX, float dotVY, float ax, float ay)
            {
                return 1.0 / (1.0 + sqrt( (pow(dotVX * ax, 2.0) + pow(dotVY * ay, 2.0)) / pow(dotVN, 2.0)));
            }
            //G2
            float GeometrySmith_aniso(float3 N, float3 V, float3 L, float roughnessX,float roughnessY,float3 X,float3 Y)
            {
                float dotVN = dot(N,V);
                float dotVX = dot(V,X);
                float dotVY = dot(V,Y);
                float dotLN = dot(L,N);
                float dotLX = dot(L,X);
                float dotLY = dot(L,Y);
                float ggx2 = smithG_GGX_aniso(dotVN,dotVX,dotVY,roughnessX,roughnessY);
                float ggx1 = smithG_GGX_aniso(dotLN,dotLX,dotLY,roughnessX,roughnessY);
                if(dotVN <0.0 || dotLN <0.0)return 0.0;
                return ggx1 * ggx2;
            }

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = TRANSFORM_TEX(v.uv, _MainTex);
                o.worldNormal = normalize(UnityObjectToWorldNormal(v.normal));
                o.worldPos = mul(unity_ObjectToWorld, v.vertex).xyz;
                o.worldTangent = normalize(UnityObjectToWorldDir(v.tangent));
                o.worldBiTangent = normalize(cross(o.worldNormal , o.worldTangent));
                UNITY_TRANSFER_FOG(o,o.vertex);
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                float3 normal = normalize(i.worldNormal);
                float3 lightDir = normalize(_WorldSpaceLightPos0);
                float3 cameraDir = normalize(_WorldSpaceCameraPos - i.worldPos);
                float3 tangent = normalize(i.worldTangent);
                float3 bitangent = normalize(i.worldBiTangent);

                float NdotL = dot(normal,lightDir);
                float NdotV = dot(normal,cameraDir);
                
                float3 H = normalize(lightDir+cameraDir);

                float F = fresnel(lightDir,normal,1.0,_IOR);
                float G = GeometrySmith_aniso(normal,cameraDir,lightDir,_RoughnessX,_RoughnessY,tangent,bitangent);
                float D = DistributionGGX_Aniso(_RoughnessX,_RoughnessY,dot(normal,H),H,tangent,bitangent);

                float f = F * G * D / (4 * NdotL * NdotV);

                //还没熟悉Unity的光源，先用这个了
                float3 lightRadiance = (1.0,1.0,1.0);

                float3 texColor = tex2D(_MainTex,i.uv);
                float3 color = f * NdotL * lightRadiance *texColor;

                if(NdotL<0.0)color = float3(0.0,0.0,0.0);

                //因为只有单次光线弹射，物体的背面是黑色的，为了美观加了一个环境光
                float3 ambient = float3(0.1,0.1,0.1) * texColor;
                color += ambient;

                return float4(color,1.0);
            }
            ENDCG
        }
    }
}

实现的效果

使用了Unity默认的球模型，参数如下图所示，这是对球进行上下打磨后产生的高光作用效果

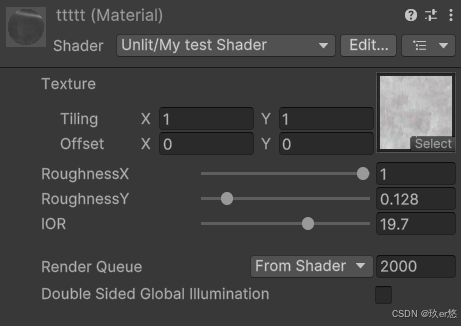
对球左右打磨后的高光作用效果，参数如下图所示

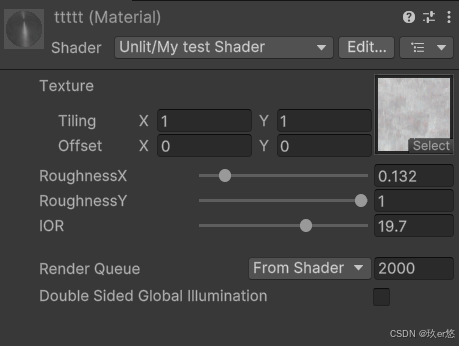
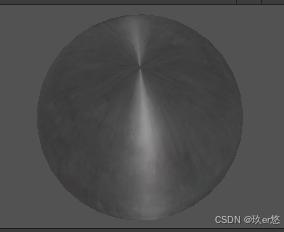
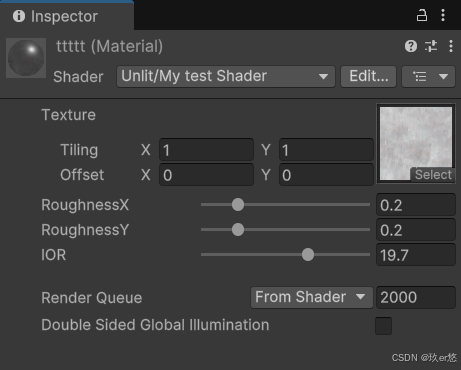
将两个方向的粗糙度设置为一样，重新回到了各向同性的高光效果，参数如下图所示

参考

1\][【PBR系列五】镜面反射BRDF模型(Specular BRDF)及实现效果](https://blog.csdn.net/qq_35312463/article/details/108123270 "【PBR系列五】镜面反射BRDF模型(Specular BRDF)及实现效果") \[2\] [PBR 四 法线分布函数](https://blog.csdn.net/haozi2008/article/details/111225017 "PBR 四 法线分布函数") \[3\] [PBR 五 几何遮蔽函数](https://blog.csdn.net/haozi2008/article/details/112284028 "PBR 五 几何遮蔽函数")