引言
还是基于Sentence-BERT架构,或者说Bi-Encoder架构,但是本文使用的是苏神提出的CoSENT损失函数[1](#1)。
点击来都是缘分,之前过时的方法可以不细看,别的文章可以不收藏,现在是最流行的方法,这篇文章建议收藏!
架构
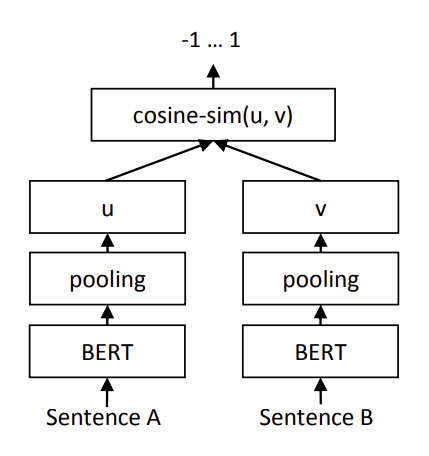
正如苏神所说的,参考了Circle Loss[2](#2)理论,这里尝试详细展开一下。
绝大多数损失函数,都在拉近相似的句子对,推远不相似的句子对,即最大化类内相似性( s p s_p sp)同时最小化类间相似性( s n s_n sn)。综合起来,实际上在减少 s n − s p s_n -s_p sn−sp,增加 s p s_p sp等同于减少 s n s_n sn。
这里我们还是用余弦相似度来衡量这个相似性,记 Ω p o s \Omega_{pos} Ωpos为所有正样本对(标签为1的样本对)集合, Ω n e g \Omega_{neg} Ωneg为所有负样本对(标签为0的样本对)的集合,所以我们希望任意的第 i i i个正样本对 i ∈ Ω p o s i \in \Omega_{pos} i∈Ωpos和任意的第 j j j个负样本对 j ∈ Ω n e g j \in \Omega_{neg} j∈Ωneg都有:
cos ( u i , v i ) > cos ( u j , v j ) (1) \cos(\pmb u_i,\pmb v_i) > \cos(\pmb u_j, \pmb v_j) \tag 1 cos(ui,vi)>cos(uj,vj)(1)
其中 u , v \pmb u,\pmb v u,v都是句向量。这里我们只希望正样本对的相似性要大于负样本对的相似性,具体大多少由模型自己决定,即这里只是判断一个相对顺序而不是具体的值。
这里我们希望减少下式:
cos ( u j , v j ) − cos ( u i , v i ) (2) \cos(\pmb u_j, \pmb v_j) - \cos(\pmb u_i,\pmb v_i) \tag 2 cos(uj,vj)−cos(ui,vi)(2)
记住这种表达形式。我们再来看交叉熵损失。

上图是Softmax CrossEntropy Loss的图示,它应用于单标签分类中, s s s是logits。
我们来回顾下这个损失函数的公式(假设 y i = 1 y j = 0 ∀ j ≠ i y_i=1 \,\, y_j = 0 \,\, \forall j \neq i yi=1yj=0∀j=i):
L = − y i log p i = − log ( e s i ∑ j e s j ) = − log ( e s i ⋅ e − s i e − s i ⋅ ∑ j e s j ) = − log ( 1 ∑ j e s j − s i ) = log ( ∑ j e s j − s i ) = log ( 1 + ∑ j , j ≠ i e s j − s i ) (3) \begin{aligned} \mathcal L &= - y_i \log p_i \\ &= -\log \left( \frac{e^{s_i}}{\sum_j e^{s_j}}\right) \\ &= -\log \left( \frac{e^{s_i} \cdot e^{ -s_i}}{e^{ -s_i} \cdot \sum_j e^{s_j}}\right) \\ &= -\log \left( \frac{1}{\sum_j e^{s_j - s_i}}\right) \\ &= \log \left( \sum_j e^{s_j - s_i}\right) \\ &= \log \left(1 + \sum_{j, j\neq i} e^{s_j - s_i}\right) \end{aligned} \tag 3 L=−yilogpi=−log(∑jesjesi)=−log(e−si⋅∑jesjesi⋅e−si)=−log(∑jesj−si1)=log(j∑esj−si)=log 1+j,j=i∑esj−si (3)
最后一步将 e s i − s i e^{s_i - s_i} esi−si拿到求和符号外面来了,表达了希望减小 s j − s i s_j -s_i sj−si的意思。
用于多分类任务时,假设有很多个类别,但只有一个类别取值为1,其他取值为0。多分类任务时这里的 s s s为logits。注意我们这里希望 s i s_i si越大越好,要比其他的 s j s_j sj要大。
同时,假如我们用 s s s表示一个句子对之间的相似度,即 s = cos ( u , v ) s = \cos(\pmb u, \pmb v) s=cos(u,v)。
结合式子(2)我们可以得到一个损失:
log ( 1 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e s j − s i ) = log ( 1 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e cos ( u j , v j ) − cos ( u i , v i ) ) (4) \log \left(1 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{s_j - s_i}\right) = \log \left(1 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{\cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i)}\right) \tag 4 log 1+i∈Ωpos,j∈Ωneg∑esj−si =log 1+i∈Ωpos,j∈Ωneg∑ecos(uj,vj)−cos(ui,vi) (4)
然后类似Circle Loss,增加一个超参数 λ > 0 \lambda >0 λ>0,就得到了最终的CoSENT Loss表达式:
log ( 1 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e λ ( cos ( u j , v j ) − cos ( u i , v i ) ) ) (5) \log \left(1 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{\lambda (\cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i))}\right) \tag 5 log 1+i∈Ωpos,j∈Ωneg∑eλ(cos(uj,vj)−cos(ui,vi)) (5)
这里 λ \lambda λ默认等于 20 20 20,相当于除以温度系数 0.05 0.05 0.05。
理论部分完毕,现在来看实现。
实现
实现采用类似Huggingface的形式,每个文件夹下面有一种模型。分为modeling、arguments、trainer等不同的文件。不同的架构放置在不同的文件夹内。
modeling.py:
py
from dataclasses import dataclass
import torch
from torch import Tensor, nn
from transformers.file_utils import ModelOutput
from transformers import (
AutoModel,
AutoTokenizer,
)
import numpy as np
from tqdm.autonotebook import trange
from typing import Optional
import torch.nn.functional as F
@dataclass
class BiOutput(ModelOutput):
loss: Optional[Tensor] = None
scores: Optional[Tensor] = None
class SentenceBert(nn.Module):
def __init__(
self,
model_name: str,
trust_remote_code: bool = True,
max_length: int = None,
scale: float = 20.0,
pooling_mode: str = "mean",
normalize_embeddings: bool = False,
) -> None:
super().__init__()
self.model_name = model_name
self.normalize_embeddings = normalize_embeddings
self.device = "cuda" if torch.cuda.is_available() else "cpu"
self.tokenizer = AutoTokenizer.from_pretrained(
model_name, trust_remote_code=trust_remote_code
)
self.model = AutoModel.from_pretrained(
model_name, trust_remote_code=trust_remote_code
).to(self.device)
self.max_length = max_length
self.pooling_mode = pooling_mode
self.scale = scale
def sentence_embedding(self, last_hidden_state, attention_mask):
if self.pooling_mode == "mean":
attention_mask = attention_mask.unsqueeze(-1).float()
return torch.sum(last_hidden_state * attention_mask, dim=1) / torch.clamp(
attention_mask.sum(1), min=1e-9
)
else:
# cls
return last_hidden_state[:, 0]
def encode(
self,
sentences: str | list[str],
batch_size: int = 64,
convert_to_tensor: bool = True,
show_progress_bar: bool = False,
):
if isinstance(sentences, str):
sentences = [sentences]
all_embeddings = []
for start_index in trange(
0, len(sentences), batch_size, desc="Batches", disable=not show_progress_bar
):
batch = sentences[start_index : start_index + batch_size]
features = self.tokenizer(
batch,
padding=True,
truncation=True,
return_tensors="pt",
return_attention_mask=True,
max_length=self.max_length,
).to(self.device)
out_features = self.model(**features, return_dict=True)
embeddings = self.sentence_embedding(
out_features.last_hidden_state, features["attention_mask"]
)
if not self.training:
embeddings = embeddings.detach()
if self.normalize_embeddings:
embeddings = torch.nn.functional.normalize(embeddings, p=2, dim=1)
if not convert_to_tensor:
embeddings = embeddings.cpu()
all_embeddings.extend(embeddings)
if convert_to_tensor:
all_embeddings = torch.stack(all_embeddings)
else:
all_embeddings = np.asarray([emb.numpy() for emb in all_embeddings])
return all_embeddings
def compute_loss(self, scores, labels):
"""
Args:
scores : (batch_size)
labels : (labels)
"""
labels = torch.tensor(labels).to(self.device)
scores = scores * self.scale
# (batch_size, 1) - (1, batch_size)
# scores (batch_size, batch_size)
scores = scores[:, None] - scores[None, :]
# labels (batch_size, batch_size)
labels = labels[:, None] < labels[None, :]
labels = labels.float()
# mask out irrelevant pairs so they are negligible after exp()
scores = scores - (1 - labels) * 1e12
# append a zero as e^0 = 1
scores = torch.cat((torch.zeros(1).to(self.device), scores.view(-1)), dim=0)
loss = torch.logsumexp(scores, dim=0)
return loss
def forward(self, source, target, labels) -> BiOutput:
"""
Args:
source :
target :
"""
# source_embed (batch_size, embed_dim)
source_embed = self.encode(source)
# target_embed (batch_size, embed_dim)
target_embed = self.encode(target)
# scores (batch_size)
scores = F.cosine_similarity(source_embed, target_embed)
loss = self.compute_loss(scores, labels)
return BiOutput(loss, scores)
def save_pretrained(self, output_dir: str):
state_dict = self.model.state_dict()
state_dict = type(state_dict)(
{k: v.clone().cpu().contiguous() for k, v in state_dict.items()}
)
self.model.save_pretrained(output_dir, state_dict=state_dict)整个模型的实现放到modeling.py文件中。
py
def compute_loss(self, scores, labels):
"""
Args:
scores : (batch_size)
labels : (labels)
"""
labels = torch.tensor(labels).to(self.device)
scores = scores * self.scale
# (batch_size, 1) - (1, batch_size)
# scores (batch_size, batch_size)
scores = scores[:, None] - scores[None, :]
# labels (batch_size, batch_size)
labels = labels[:, None] < labels[None, :]
labels = labels.float()
# mask out irrelevant pairs so they are negligible after exp()
scores = scores - (1 - labels) * 1e12
# append a zero as e^0 = 1
scores = torch.cat((torch.zeros(1).to(self.device), scores.view(-1)), dim=0)
loss = torch.logsumexp(scores, dim=0)
return loss由于compute_loss这部分还有点复杂,这里也展开分析一下。首先我们回顾一下公式(5):
log ( 1 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e λ ( cos ( u j , v j ) − cos ( u i , v i ) ) ) = log ( e 0 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e λ ( cos ( u j , v j ) − cos ( u i , v i ) ) ) \log \left(1 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{\lambda (\cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i))}\right) = \log \left( e^0 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{\lambda (\cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i))} \right ) log 1+i∈Ωpos,j∈Ωneg∑eλ(cos(uj,vj)−cos(ui,vi)) =log e0+i∈Ωpos,j∈Ωneg∑eλ(cos(uj,vj)−cos(ui,vi))
以一个例子来分析这个函数:
py
import torch
from torch import Tensor
import torch.nn.functional as F
from transformers import set_seed
set_seed(0)
batch_size = 6
embedding_dim = 64
# 随机初始化
source, target = torch.randn((batch_size, embedding_dim)), torch.randn((batch_size, embedding_dim))
# 定义标签, 1表示相似, 0表示不相似
labels = torch.tensor([0, 1, 1, 0, 1, 0])这里假设批次内有6对样本,设置了每对样本的标签。
py
scores = F.cosine_similarity(source, target)
print(scores)
python
tensor([-0.0816, -0.1727, -0.2052, 0.0240, 0.2252, 0.0084])计算对内的余弦相似度得分。
py
scores = scores * 20
scores
python
tensor([-1.6312, -3.4543, -4.1032, 0.4800, 4.5039, 0.1671])乘上缩放因子 λ \lambda λ。
py
# (batch_size, 1) - (1, batch_size)
# scores (batch_size, batch_size)
# 负例减正例的差值
scores = scores[:, None] - scores[None, :]
scores
py
tensor([[ 0.0000, 1.8231, 2.4720, -2.1113, -6.1351, -1.7984],
[-1.8231, 0.0000, 0.6489, -3.9343, -7.9582, -3.6214],
[-2.4720, -0.6489, 0.0000, -4.5832, -8.6071, -4.2703],
[ 2.1113, 3.9343, 4.5832, 0.0000, -4.0238, 0.3129],
[ 6.1351, 7.9582, 8.6071, 4.0238, 0.0000, 4.3367],
[ 1.7984, 3.6214, 4.2703, -0.3129, -4.3367, 0.0000]])scores[:, None]结果是一个(batch_size, 1)的张量,经过广播(按列广播)会变成(batch_size, batch_size):
py
tensor([[-1.6312, -1.6312, -1.6312, -1.6312, -1.6312, -1.6312],
[-3.4543, -3.4543, -3.4543, -3.4543, -3.4543, -3.4543],
[-4.1032, -4.1032, -4.1032, -4.1032, -4.1032, -4.1032],
[ 0.4800, 0.4800, 0.4800, 0.4800, 0.4800, 0.4800],
[ 4.5039, 4.5039, 4.5039, 4.5039, 4.5039, 4.5039],
[ 0.1671, 0.1671, 0.1671, 0.1671, 0.1671, 0.1671]])scores[None, :]结果是一个(1, batch_size)的张量,经过广播(按行广播)会变成(batch_size, batch_size):
py
tensor([[ 0.0000, 1.8231, 2.4720, -2.1113, -6.1351, -1.7984],
[-1.8231, 0.0000, 0.6489, -3.9343, -7.9582, -3.6214],
[-2.4720, -0.6489, 0.0000, -4.5832, -8.6071, -4.2703],
[ 2.1113, 3.9343, 4.5832, 0.0000, -4.0238, 0.3129],
[ 6.1351, 7.9582, 8.6071, 4.0238, 0.0000, 4.3367],
[ 1.7984, 3.6214, 4.2703, -0.3129, -4.3367, 0.0000]])第一个减去第二个刚好也得:
py
tensor([[ 0.0000, 1.8231, 2.4720, -2.1113, -6.1351, -1.7984],
[-1.8231, 0.0000, 0.6489, -3.9343, -7.9582, -3.6214],
[-2.4720, -0.6489, 0.0000, -4.5832, -8.6071, -4.2703],
[ 2.1113, 3.9343, 4.5832, 0.0000, -4.0238, 0.3129],
[ 6.1351, 7.9582, 8.6071, 4.0238, 0.0000, 4.3367],
[ 1.7984, 3.6214, 4.2703, -0.3129, -4.3367, 0.0000]])实际上是计算原scores列表第j个元素(语句对的相似度)减去第i个元素(语句对的相似度)的差值,对应上面矩阵的[j,i]处,即 cos ( u j , v j ) − cos ( u i , v i ) \cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i) cos(uj,vj)−cos(ui,vi)。
我们可以画图感受一下:
py
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
scores_np = scores.numpy()
# 使用 seaborn 绘制热力图
plt.figure(figsize=(8, 6))
sns.heatmap(scores_np, annot=True, cmap='coolwarm', fmt='.2f', linecolor='white', linewidth=0.1)
plt.title('Scores Matrix')
plt.show()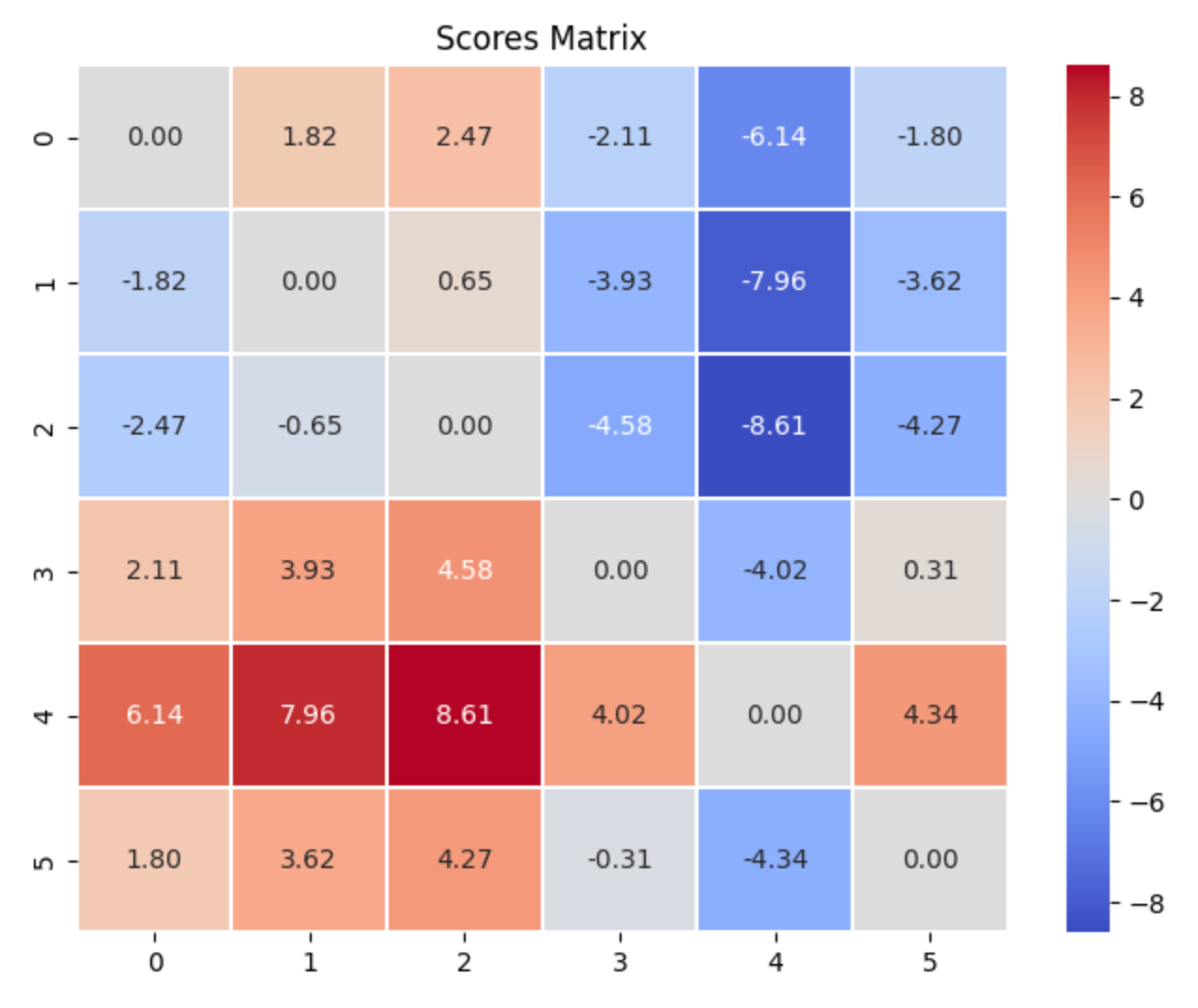
下面我们关心的是 j ∈ Ω n e g ∧ i ∈ Ω p o s j \in \Omega_{neg} ∧ i \in \Omega_{pos} j∈Ωneg∧i∈Ωpos的情形。
py
scores.shape
python
torch.Size([6, 6])先确认下形状为(batch_size, batch_size)。
py
labels = labels[:, None] < labels[None, :]
labels = labels.float()
# labels[j][i] 表示是否第j个语句对的标签 是否 小于 第 i 个
labels
python
# j 0 1 2 3 4 5 i
tensor([[0., 1., 1., 0., 1., 0.],# 0
[0., 0., 0., 0., 0., 0.],# 1
[0., 0., 0., 0., 0., 0.],# 2
[0., 1., 1., 0., 1., 0.],# 3
[0., 0., 0., 0., 0., 0.],# 4
[0., 1., 1., 0., 1., 0.]])#5第j个语句对的标签小于 第 i 个满足我们的要求: j ∈ Ω n e g ∧ i ∈ Ω p o s j \in \Omega_{neg} ∧ i \in \Omega_{pos} j∈Ωneg∧i∈Ωpos,也就是说下面矩阵取值为 1 1 1的元素是我们关心的。
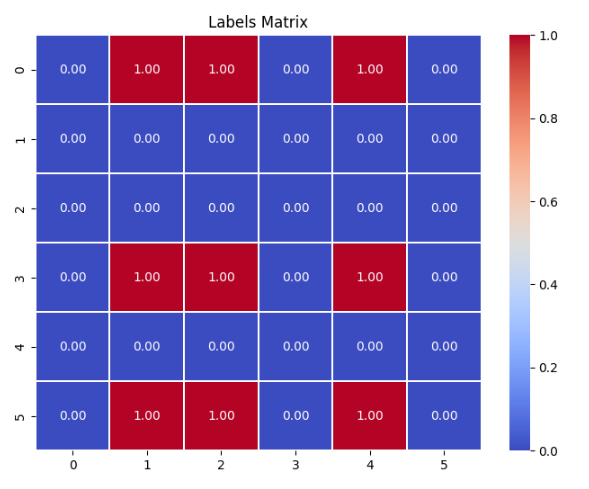
我们也画出这个labels矩阵。
py
scores = scores - (1 - labels) * 1e12把新矩阵labels=0处的元素减去一个负的比较大的数,负的大的数计算指数后变成0,即我们不关心labels取 0 0 0对应的元素。只关心 j ∈ Ω n e g ∧ i ∈ Ω p o s j \in \Omega_{neg} ∧ i \in \Omega_{pos} j∈Ωneg∧i∈Ωpos的。
现在scores都是我们关心的值,然后还缺一个 e 0 e^0 e0:
py
scores = torch.cat((torch.zeros(1).to(self.device), scores.view(-1)), dim=0)log ( e 0 + ∑ i ∈ Ω p o s , j ∈ Ω n e g e λ ( cos ( u j , v j ) − cos ( u i , v i ) ) ) \log \left( e^0 + \sum_{i \in \Omega_{pos}, j \in \Omega_{neg}} e^{\lambda (\cos(\pmb u_j,\pmb v_j)- \cos(\pmb u_i,\pmb v_i))} \right ) log e0+i∈Ωpos,j∈Ωneg∑eλ(cos(uj,vj)−cos(ui,vi))
如上公式所示。
最后加一个logsumexp:
py
loss = torch.logsumexp(scores, dim=0)得到最终的损失。
完毕。
arguments.py:
python
from dataclasses import dataclass, field
from typing import Optional
import os
@dataclass
class ModelArguments:
model_name_or_path: str = field(
metadata={
"help": "Path to pretrained model"
}
)
config_name: Optional[str] = field(
default=None,
metadata={
"help": "Pretrained config name or path if not the same as model_name"
},
)
tokenizer_name: Optional[str] = field(
default=None,
metadata={
"help": "Pretrained tokenizer name or path if not the same as model_name"
},
)
@dataclass
class DataArguments:
train_data_path: str = field(
default=None, metadata={"help": "Path to train corpus"}
)
eval_data_path: str = field(default=None, metadata={"help": "Path to eval corpus"})
max_length: int = field(
default=512,
metadata={
"help": "The maximum total input sequence length after tokenization for input text."
},
)
def __post_init__(self):
if not os.path.exists(self.train_data_path):
raise FileNotFoundError(
f"cannot find file: {self.train_data_path}, please set a true path"
)
if not os.path.exists(self.eval_data_path):
raise FileNotFoundError(
f"cannot find file: {self.eval_data_path}, please set a true path"
)定义了模型和数据相关参数。
dataset.py:
python
from torch.utils.data import Dataset
from datasets import Dataset as dt
import pandas as pd
from utils import build_dataframe_from_csv
class PairDataset(Dataset):
def __init__(self, data_path: str) -> None:
df = build_dataframe_from_csv(data_path)
self.dataset = dt.from_pandas(df, split="train")
self.total_len = len(self.dataset)
def __len__(self):
return self.total_len
def __getitem__(self, index) -> dict[str, str]:
query1 = self.dataset[index]["query1"]
query2 = self.dataset[index]["query2"]
label = self.dataset[index]["label"]
return {"query1": query1, "query2": query2, "label": label}
class PairCollator:
def __call__(self, features) -> dict[str, list[str]]:
queries1 = []
queries2 = []
labels = []
for feature in features:
queries1.append(feature["query1"])
queries2.append(feature["query2"])
labels.append(feature["label"])
return {"source": queries1, "target": queries2, "labels": labels}数据集类考虑了LCQMC数据集的格式,即成对的语句和一个数值标签。类似:
Hello. Hi. 1
Nice to see you. Nice 0trainer.py:
py
import torch
from transformers.trainer import Trainer
from typing import Optional
import os
import logging
from modeling import SentenceBert
TRAINING_ARGS_NAME = "training_args.bin"
logger = logging.getLogger(__name__)
class BiTrainer(Trainer):
def compute_loss(self, model: SentenceBert, inputs, return_outputs=False):
outputs = model(**inputs)
loss = outputs.loss
return (loss, outputs) if return_outputs else loss
def _save(self, output_dir: Optional[str] = None, state_dict=None):
# If we are executing this function, we are the process zero, so we don't check for that.
output_dir = output_dir if output_dir is not None else self.args.output_dir
os.makedirs(output_dir, exist_ok=True)
logger.info(f"Saving model checkpoint to {output_dir}")
self.model.save_pretrained(output_dir)
if self.tokenizer is not None:
self.tokenizer.save_pretrained(output_dir)
# Good practice: save your training arguments together with the trained model
torch.save(self.args, os.path.join(output_dir, TRAINING_ARGS_NAME))继承🤗 Transformers的Trainer类,重写了compute_loss和_save方法。
这样我们就可以利用🤗 Transformers来训练我们的模型了。
utils.py:
python
import torch
import pandas as pd
from scipy.stats import pearsonr, spearmanr
from typing import Tuple
def build_dataframe_from_csv(dataset_csv: str) -> pd.DataFrame:
df = pd.read_csv(
dataset_csv,
sep="\t",
header=None,
names=["query1", "query2", "label"],
)
return df
def compute_spearmanr(x, y):
return spearmanr(x, y).correlation
def compute_pearsonr(x, y):
return pearsonr(x, y)[0]
def find_best_acc_and_threshold(scores, labels, high_score_more_similar: bool):
"""Copied from https://github.com/UKPLab/sentence-transformers/tree/master"""
assert len(scores) == len(labels)
rows = list(zip(scores, labels))
rows = sorted(rows, key=lambda x: x[0], reverse=high_score_more_similar)
print(rows)
max_acc = 0
best_threshold = -1
# positive examples number so far
positive_so_far = 0
# remain negative examples
remaining_negatives = sum(labels == 0)
for i in range(len(rows) - 1):
score, label = rows[i]
if label == 1:
positive_so_far += 1
else:
remaining_negatives -= 1
acc = (positive_so_far + remaining_negatives) / len(labels)
if acc > max_acc:
max_acc = acc
best_threshold = (rows[i][0] + rows[i + 1][0]) / 2
return max_acc, best_threshold
def metrics(y: torch.Tensor, y_pred: torch.Tensor) -> Tuple[float, float, float, float]:
TP = ((y_pred == 1) & (y == 1)).sum().float() # True Positive
TN = ((y_pred == 0) & (y == 0)).sum().float() # True Negative
FN = ((y_pred == 0) & (y == 1)).sum().float() # False Negatvie
FP = ((y_pred == 1) & (y == 0)).sum().float() # False Positive
p = TP / (TP + FP).clamp(min=1e-8) # Precision
r = TP / (TP + FN).clamp(min=1e-8) # Recall
F1 = 2 * r * p / (r + p).clamp(min=1e-8) # F1 score
acc = (TP + TN) / (TP + TN + FP + FN).clamp(min=1e-8) # Accurary
return acc, p, r, F1
def compute_metrics(predicts, labels):
return metrics(labels, predicts)定义了一些帮助函数,从sentence-transformers库中拷贝了寻找最佳准确率阈值的实现find_best_acc_and_threshold。
除了准确率,还计算了句嵌入的余弦相似度与真实标签之间的斯皮尔曼等级相关系数指标。
最后定义训练和测试脚本。
train.py:
python
from transformers import set_seed, HfArgumentParser, TrainingArguments
import logging
from pathlib import Path
from datetime import datetime
from modeling import SentenceBert
from trainer import BiTrainer
from arguments import DataArguments, ModelArguments
from dataset import PairCollator, PairDataset
logger = logging.getLogger(__name__)
logging.basicConfig(
format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
datefmt="%m/%d/%Y %H:%M:%S",
level=logging.INFO,
)
def main():
parser = HfArgumentParser((TrainingArguments, DataArguments, ModelArguments))
training_args, data_args, model_args = parser.parse_args_into_dataclasses()
# 根据当前时间生成输出目录
output_dir = f"{training_args.output_dir}/{model_args.model_name_or_path.replace('/', '-')}-{datetime.now().strftime('%Y-%m-%d_%H-%M-%S')}"
training_args.output_dir = output_dir
logger.info(f"Training parameters {training_args}")
logger.info(f"Data parameters {data_args}")
logger.info(f"Model parameters {model_args}")
# 设置随机种子
set_seed(training_args.seed)
# 加载预训练模型
model = SentenceBert(
model_args.model_name_or_path,
trust_remote_code=True,
max_length=data_args.max_length,
)
tokenizer = model.tokenizer
# 构建训练和测试集
train_dataset = PairDataset(data_args.train_data_path)
eval_dataset = PairDataset(data_args.eval_data_path)
# 传入参数
trainer = BiTrainer(
model=model,
args=training_args,
train_dataset=train_dataset,
eval_dataset=eval_dataset,
data_collator=PairCollator(),
tokenizer=tokenizer,
)
Path(training_args.output_dir).mkdir(parents=True, exist_ok=True)
# 开始训练
trainer.train()
trainer.save_model()
if __name__ == "__main__":
main()训练
基于train.py定义了train.sh传入相关参数:
sh
timestamp=$(date +%Y%m%d%H%M)
logfile="train_${timestamp}.log"
# change CUDA_VISIBLE_DEVICES
CUDA_VISIBLE_DEVICES=3 nohup python train.py \
--model_name_or_path=hfl/chinese-macbert-large \
--output_dir=output \
--train_data_path=data/train.txt \
--eval_data_path=data/dev.txt \
--num_train_epochs=3 \
--save_total_limit=5 \
--learning_rate=2e-5 \
--weight_decay=0.01 \
--warmup_ratio=0.01 \
--bf16=True \
--eval_strategy=epoch \
--save_strategy=epoch \
--per_device_train_batch_size=64 \
--report_to="none" \
--remove_unused_columns=False \
--max_length=128 \
> "$logfile" 2>&1 &以上参数根据个人环境修改,这里使用的是哈工大的chinese-macbert-large预训练模型。
注意:
-
--remove_unused_columns是必须的。 -
通过
bf16=True可以加速训练同时不影响效果。 -
其他参数可以自己调整。
100%|██████████| 11193/11193 [46:54<00:00, 4.35it/s]
100%|██████████| 11193/11193 [46:54<00:00, 3.98it/s]
09/05/2024 17:35:20 - INFO - trainer - Saving model checkpoint to output/hfl-chinese-macbert-large-2024-09-05_18-48-21
{'eval_loss': 0.9763002395629883, 'eval_runtime': 56.9409, 'eval_samples_per_second': 154.581, 'eval_steps_per_second': 19.336, 'epoch': 3.0}
{'train_runtime': 2814.5056, 'train_samples_per_second': 254.502, 'train_steps_per_second': 3.977, 'train_loss': 4.296681343023402, 'epoch': 3.0}
这里仅训练了3轮,我们拿最后保存的模型output/hfl-chinese-macbert-large-2024-09-05_18-48-21进行测试。
测试
test.py: 测试脚本见后文的完整代码。
test.sh:
sh
# change CUDA_VISIBLE_DEVICES
CUDA_VISIBLE_DEVICES=0 python test.py \
--model_name_or_path=output/hfl-chinese-macbert-large-2024-09-05_18-48-21 \
--test_data_path=data/test.txt
输出:
TestArguments(model_name_or_path='output/hfl-chinese-macbert-large-2024-09-05_18-48-21/checkpoint-11193', test_data_path='data/test.txt', max_length=64, batch_size=128)
Batches: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 98/98 [00:11<00:00, 8.78it/s]
Batches: 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 98/98 [00:11<00:00, 8.86it/s]
max_acc: 0.8940, best_threshold: 0.839080
spearman corr: 0.7989 | pearson_corr corr: 0.7703 | compute time: 22.26s
accuracy=0.894 precision=0.911 recal=0.874 f1 score=0.8918测试集上的准确率达到89.4%,spearman系数达到了目前本系列文章的SOTA结果。
该方法计算出来的分类阈值0.839080看起来也比之前的更合理。
完整代码
完整代码: →点此←