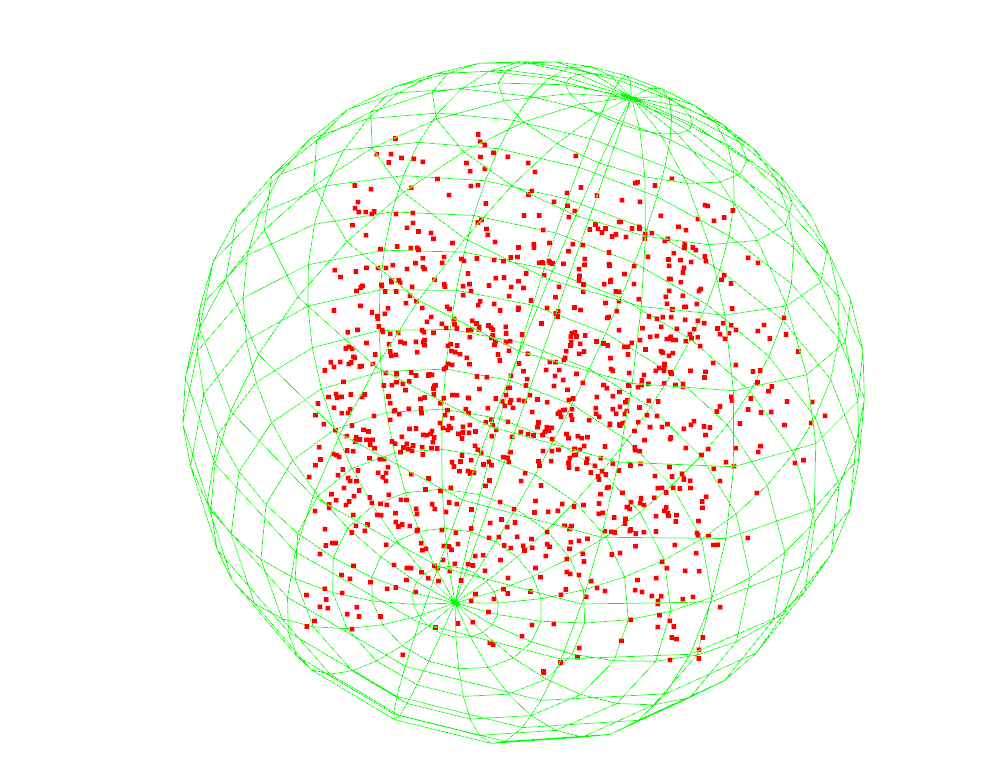
- 定义:通过一个球体包围所有点云点,该球体的球心和半径由点云的分布决定,并且球体的半径尽可能小。
- 优点:计算简单,通常用于快速粗略估计物体的范围。
- 缺点:对于不规则形状的物体,包围不紧密,容易留下较多空白区域。
下面将介绍一种常用的算法------Welzl算法,并提供Python实现的具体步骤和代码示例。
Welzl算法简介
Welzl算法是一种递归算法,用于在期望线性时间内找到一组点的最小包围球。其基本思想是随机化点的顺序,然后递归地处理每个点,决定是否需要将其包含在当前的边界集(即确定球体)的情况下更新最小包围球。
算法的核心思想是:我们逐个考虑每个点,看是否需要将它包含在球面上。如果一个点已经在当前的最小球内,我们就不需要改变球;如果不在,我们就需要重新计算球,使得这个点在新球的表面上。
实现步骤
这个实现使用了Welzl算法来计算最小包围球。以下是算法的主要步骤:
welzl_algorithm函数是算法的入口点,它调用递归函数welzl。welzl函数是算法的核心,它递归地构建包围球:- 如果没有剩余点或者已经有4个点在球面上,就直接构造球。
- 否则,它会检查当前点是否在之前构造的球内。
- 如果不在,就将该点添加到球面点集中,并重新计算球。
make_sphere函数用于从给定的点集构造球。它计算点集的中心作为球心,最远点到中心的距离作为半径。is_point_in_sphere函数检查一个点是否在给定的球内。
python
import numpy as np
def welzl_algorithm(points):
def welzl(P, R, n):
if n == 0 or len(R) == 4:
return make_sphere(R)
p = P[n-1]
sphere = welzl(P, R, n-1)
if sphere is None or not is_point_in_sphere(p, sphere):
R.append(p)
sphere = welzl(P, R, n-1)
R.pop()
return sphere
return welzl(points, [], len(points))
def make_sphere(points):
if len(points) == 0:
return None
elif len(points) == 1:
return (points[0], 0)
# 计算点集的中心和半径
center = np.mean(points, axis=0)
radius = max(np.linalg.norm(p - center) for p in points)
return (center, radius)
def is_point_in_sphere(point, sphere):
if sphere is None:
return False
center, radius = sphere
return np.linalg.norm(point - center) <= radius * (1 + 1e-6) # 添加一个小的容差
# 示例使用
if __name__ == "__main__":
# 生成一些随机的3D点
np.random.seed(0)
points = np.random.rand(20, 3) * 10
# 计算包围球
sphere = welzl_algorithm(points)
print("包围球的中心:", sphere[0])
print("包围球的半径:", sphere[1])
# 验证所有点是否都在球内
all_points_inside = all(is_point_in_sphere(p, sphere) for p in points)
print("所有点都在球内:", all_points_inside)利用open3d实现
这里使用的open3d中AABB方法得到圆的半径和直径,最后得到球形边界框
python
import open3d as o3d
import numpy as np
def compute_bounding_sphere(points):
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)
aabb = pcd.get_axis_aligned_bounding_box()
center = aabb.get_center()
radius = np.max(np.linalg.norm(points - center, axis=1))
return center, radius
def create_sphere_wireframe(center, radius, resolution=20):
theta = np.linspace(0, 2*np.pi, resolution)
phi = np.linspace(0, np.pi, resolution)
# 创建经线
meridians = []
for t in theta:
x = radius * np.cos(t) * np.sin(phi) + center[0]
y = radius * np.sin(t) * np.sin(phi) + center[1]
z = radius * np.cos(phi) + center[2]
meridian = np.column_stack((x, y, z))
meridians.append(meridian)
# 创建纬线
parallels = []
for p in phi:
x = radius * np.cos(theta) * np.sin(p) + center[0]
y = radius * np.sin(theta) * np.sin(p) + center[1]
z = radius * np.cos(p) * np.ones_like(theta) + center[2]
parallel = np.column_stack((x, y, z))
parallels.append(parallel)
# 创建线集合
line_set = o3d.geometry.LineSet()
points = np.vstack(meridians + parallels)
lines = []
for i in range(len(meridians)):
lines.extend([(i*resolution+j, i*resolution+(j+1)%resolution) for j in range(resolution)])
for i in range(len(parallels)):
lines.extend([(len(meridians)*resolution+i*resolution+j, len(meridians)*resolution+i*resolution+(j+1)%resolution) for j in range(resolution)])
line_set.points = o3d.utility.Vector3dVector(points)
line_set.lines = o3d.utility.Vector2iVector(lines)
line_set.paint_uniform_color([0, 1, 0]) # 绿色线框
return line_set
def visualize_bounding_sphere_wireframe(points, center, radius):
pcd = o3d.geometry.PointCloud()
pcd.points = o3d.utility.Vector3dVector(points)
pcd.paint_uniform_color([1, 0, 0]) # 红色点
sphere_wireframe = create_sphere_wireframe(center, radius)
# 可视化
o3d.visualization.draw_geometries([pcd, sphere_wireframe])
# 示例使用
np.random.seed(0)
points = np.random.rand(1000, 3) * 10
center, radius = compute_bounding_sphere(points)
print("包围球的中心:", center)
print("包围球的半径:", radius)
visualize_bounding_sphere_wireframe(points, center, radius)