如何理解矩阵的复数特征值和特征向量？

实数特征值的直观含义非常好理解，它就是在对应的特征向量方向上的纯拉伸/压缩。

而复数特征值，我们可以把它放在复数域中理解。但是这里给出一个不那么简洁、但是更加直观的理解方式：把它放在实空间中。那么复数特征值表现的就是旋转+等比放大/缩小。我们不妨从一个二维空间说起：

对二维空间的一个线性变换：

A=(a11a12a12a22)

假设它有两个复数特征值：

λ=a±bi=r(cos⁡θ±isin⁡θ)

以及相对应的两个特征向量：

v=(x1x2)±i(y1y2)

也就是说，虽然每个特征值都有一个实部和一个虚部（两个自由度），但是由于特征值必然是共轭成对出现的，那么两个特征值仍然只对应着一个实部和一个虚部（两个自由度）。对特征向量而言同理。

也就是说，一对复特征值给我们两个自由度，一个模，一个幅角。一对特征向量也给我们两个向量，一个是实部向量，一个是虚部向量。

于是乎，如下两个向量：

，(x1x2)， (y1y2)

就可以构成一个二维空间的一组基。

那么可以证明，当我们选取这两个向量为基时，原线性变换的表述就变成了：

B=r(cos⁡(θ)−sin⁡(θ)sin⁡(θ)cos⁡(θ))

这是一个旋转矩阵乘以一个数字。也就是说，在特征向量的实部和虚部构成的基底下，这个线性变换就是一个纯粹的旋转 θ 外加一个等比放大倍数 r 。

比如说，我们令（简化起见，选取行列式为1的矩阵）

A=(0.7−0.50.61)

这个矩阵把下图中蓝色的空间变换成红色的空间：

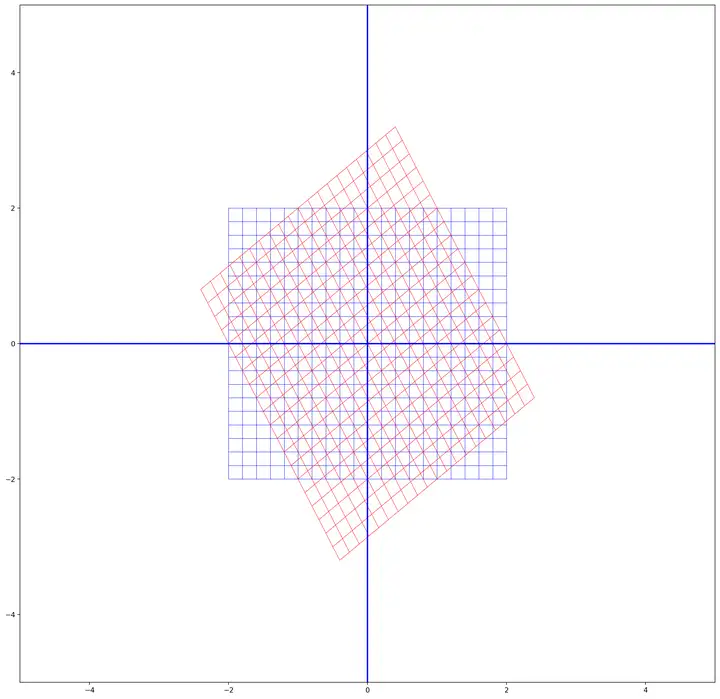
我们可以按照上述的原则进行坐标变换，变换的结果就是这样的：

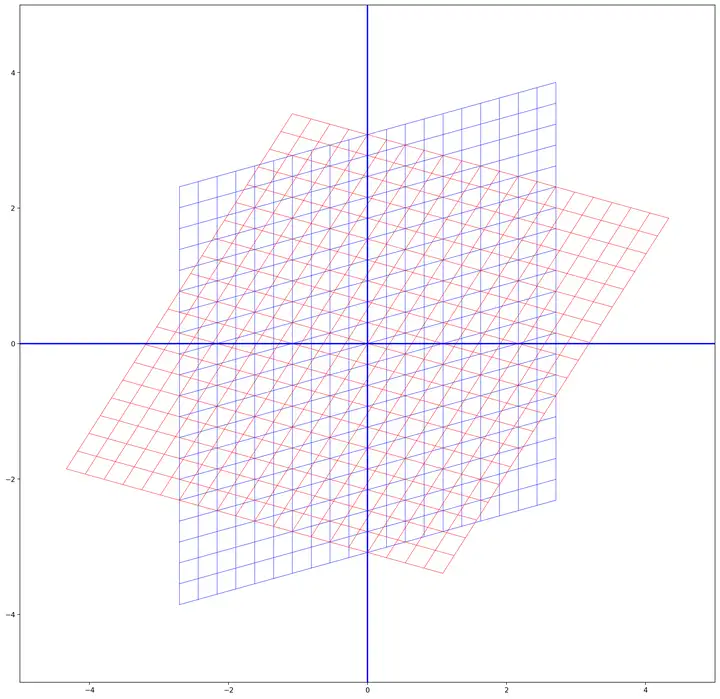
我们可以看到，经过坐标变换后，蓝色空间变为红色空间就是一个纯粹的旋转过程了。这里，复数特征值和特征向量的含义就是：

我们可以很容易推广到三维空间的变换，对一个三维矩阵：

A=(a11a12a13a21a22a23a31a32a33)

我们假设这个矩阵有三个不重叠的特征值，其中两个为共轭复数：

λ1/2=a±bi,λ3=c

那么，可以证明这个矩阵和下面这样一个分块矩阵相似，也就是说，我们可以通过选取某一个坐标系，把这个线性变换写成如下形式：

B=(ab0−ba000c)

我们令：

r=a2+b2, a=rcos⁡(θ), b=rsin⁡(θ)

那么，可以看到：

B=(cos⁡(θ)−sin⁡(θ)0sin⁡(θ)cos⁡(θ)0001)(r000r000c)

我们可以看到，这个变换就可以被分解成两个单独的变换 ，一个是纯旋转 ：在x-y平面中的旋转，另一个纯伸缩：在x-y平面上的均匀拉伸r倍，以及在z方向上单向拉伸c倍。

实现这种变换的基就是复特征向量的实部向量、虚部向量、以及实特征值的特征向量。具体讲，假定矩阵A的特征向量为：

v1/2=(x1x2x3)±i(y1y2y3), v3=(z1z2z3)

那么，这三个基底就是：

(x1x2x3), (y1y2y3), (z1z2z3)

也就是说，当我们拿到任意一个三维矩阵（注意，这里不考虑特征值重根的情况）：

如果我们继续推广到高维空间，一个线形变换可以通过上述基底的选择表示成：

{(cos⁡θ1−sin⁡θ1sinθ1cos⁡θ1)0⋯001⋯0⋮⋮⋱⋮00⋯(cos⁡θi−sin⁡θisinθicos⁡θi)}{r100⋯000r10⋯0000λ3⋯00⋮⋮⋮⋱⋮⋮00⋯ri000⋯0ri}

也是纯旋转+纯伸缩的两种变换的组合。