3. 基于协同学习机制的 CNN 肺肿瘤图像融合
3.1 网络架构
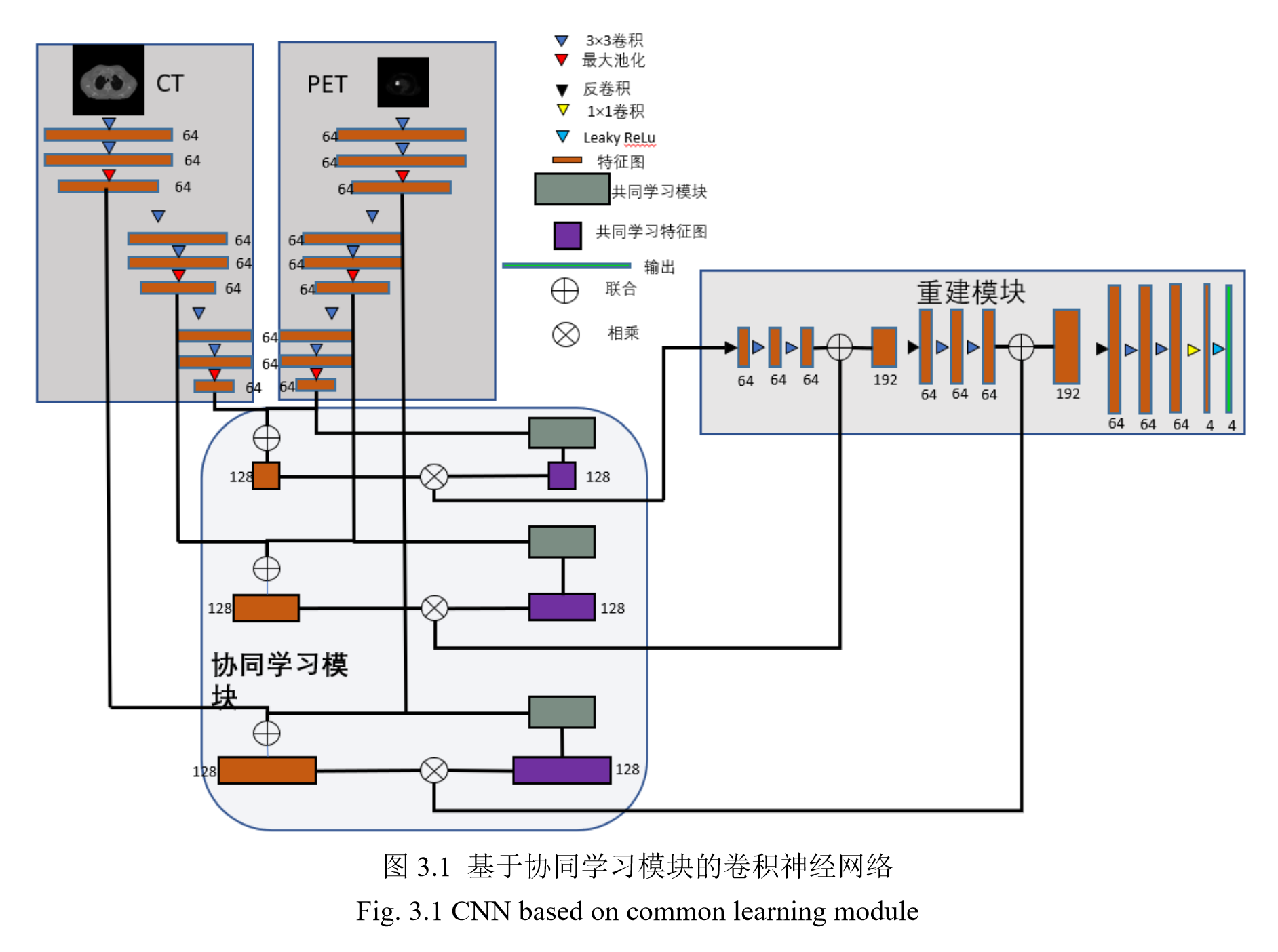
三部分:
- 两个独立的编码器
- 协同学习与融合模块
- 图像重建部分
3.1.1 特定模态编码器
编码器:
(卷积层×2+最大池化层)×3
每一 次卷积后都进行以 0 为均值,单位方差分布的归一化。
归一化之后再使用 LeakyReLU 函数进行激活。
卷积层输出:
F = L e a k y R e L U ( W ∗ X + b ) F = LeakyReLU(W*X+b) F=LeakyReLU(W∗X+b)
3.1.2 协同学习CNN激活函数
ReLU
LeakyReLU
3.1.3 协同学习CNN损失函数
交叉熵损失函数
e = − [ y l o g ( p ) + ( 1 − y ) l o g ( 1 − p ) ] e = -[ylog(p)+(1-y)log(1-p)] e=−[ylog(p)+(1−y)log(1−p)]
3.1.4 多模态特征协同学习和融合模块
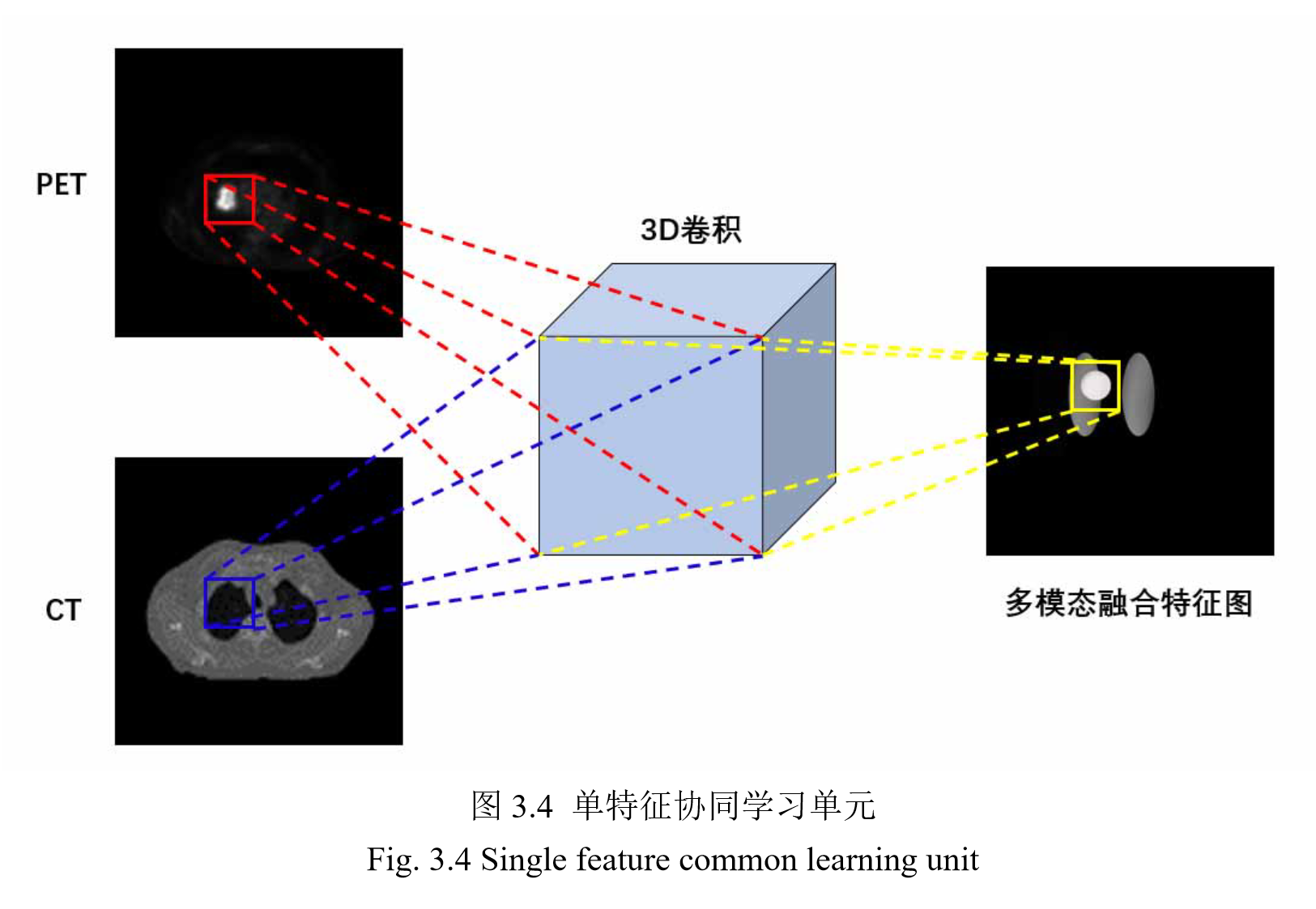
(1)协同学习
两部分:
协同学习单元
融合操作
F C T : w ∗ h ∗ c F_{CT}: w*h*c FCT:w∗h∗c
F P E T : w ∗ h ∗ c F_{PET}: w*h*c FPET:w∗h∗c
穿插堆叠: X m u l t i : w ∗ h ∗ 2 c X_{multi}: w*h*2c Xmulti:w∗h∗2c
卷积核: j ∗ j ∗ m j*j*m j∗j∗m,m是模态数=2
融合图计算公式:
F f u s i o n = L e a k y R e L U ( W m u l t i ∗ X m u l t i + b m u l t i ) F_{fusion} = LeakyReLU(W_{multi}*X_{multi}+b_{multi}) Ffusion=LeakyReLU(Wmulti∗Xmulti+bmulti)
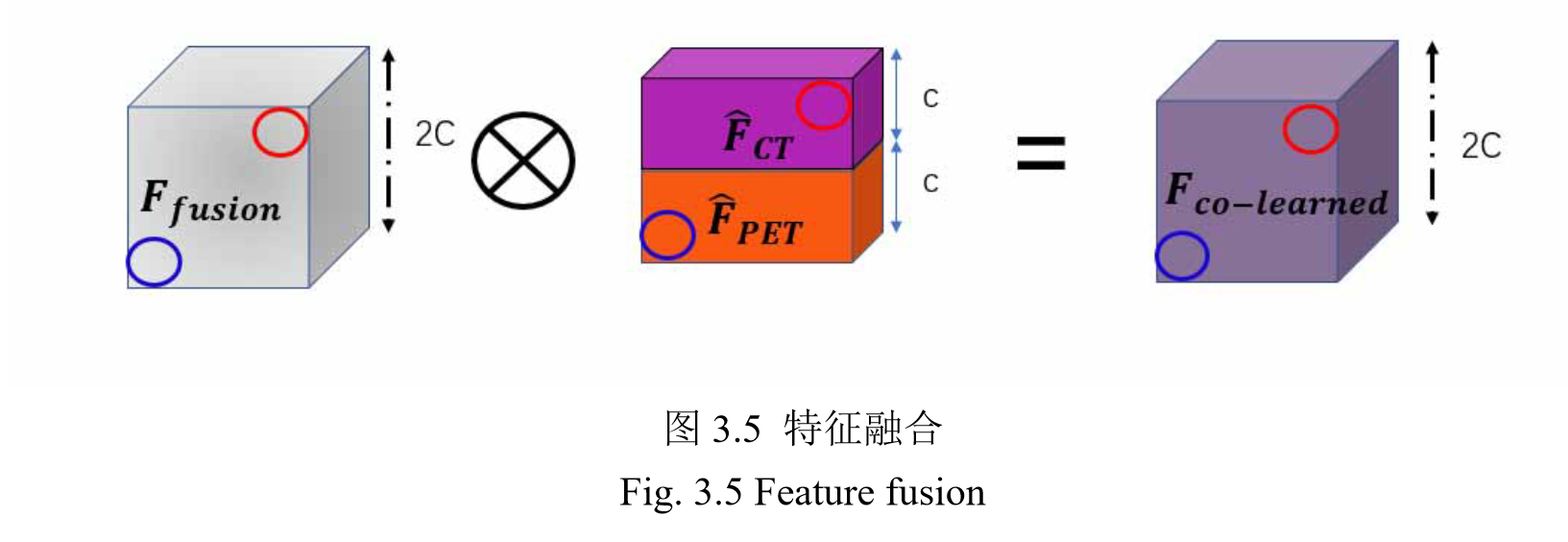
(2)融合
融合计算公式:
F c o − l e a r n e d = F f u s i o n ⊗ ( F C T ⊕ F P E T ) F_{co-learned} = F_{fusion} \otimes (F_{CT}\oplus F_{PET}) Fco−learned=Ffusion⊗(FCT⊕FPET)
像素级相乘,利用 F f u s i o n F_{fusion} Ffusion加权。
3.1.5 重建
最高一级 F f u s i o n F_{fusion} Ffusion进行一次 上采样和两次卷积,然后与比其低一级的 F f u s i o n F_{fusion} Ffusion进行堆叠,之后再次进行上述操作, 重复至所有尺度 F f u s i o n F_{fusion} Ffusion均完成以上操作。
反卷积部分 使用批量标准化和 LeakyReLU 函数进行激活。
3.2 肺肿瘤图像融合实验
PET 图像的分辨率 为 168×168,CT 图像的分辨率为 512×512。
CT 图像去除轮廓外目标。
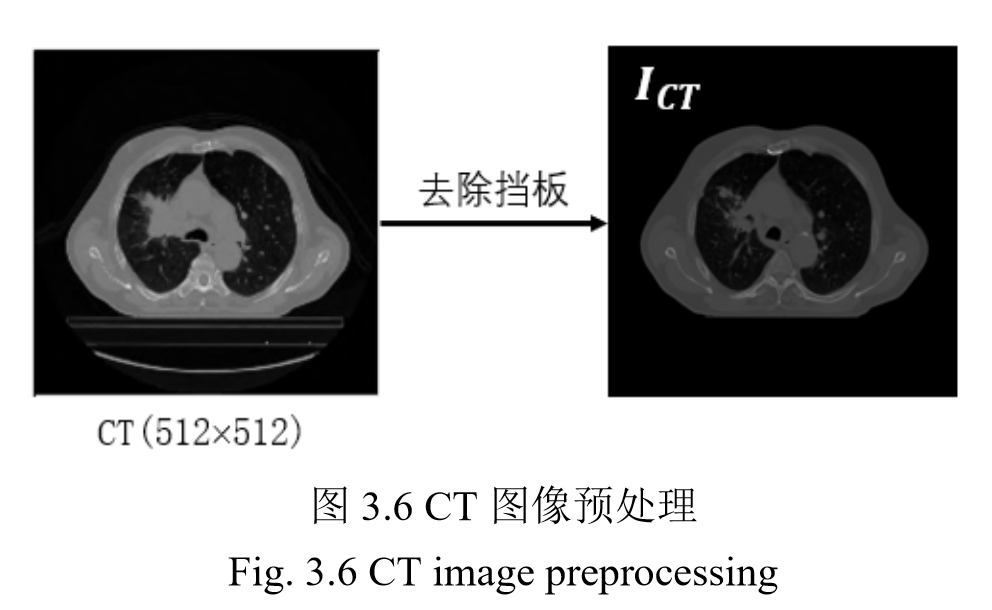
PET 图像先上采样,再配准。
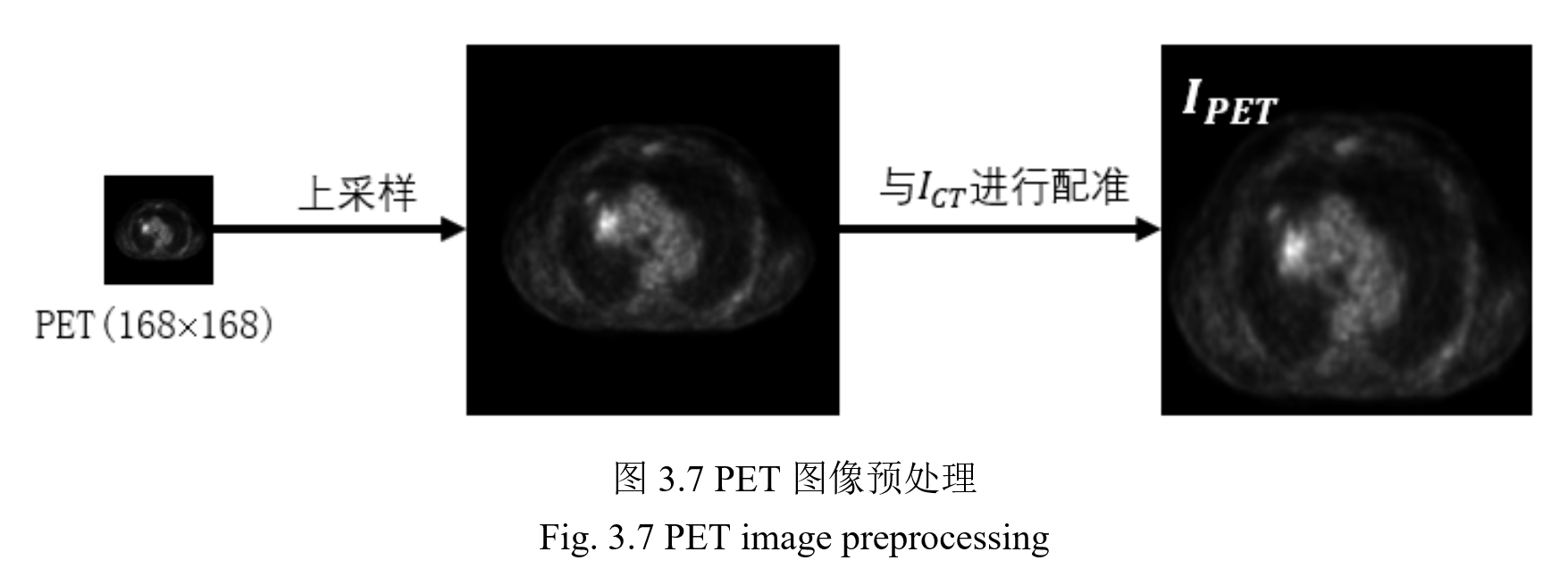
整理后共有 800 对多模态 PET/CT 肺肿瘤图片用于图像融合,经过尺度变换、裁剪等数据增强方法,将训练集扩大到 2500 对多模态图片。其中 80%用于训练,20%用于测试。
3.3 实验结果与分析
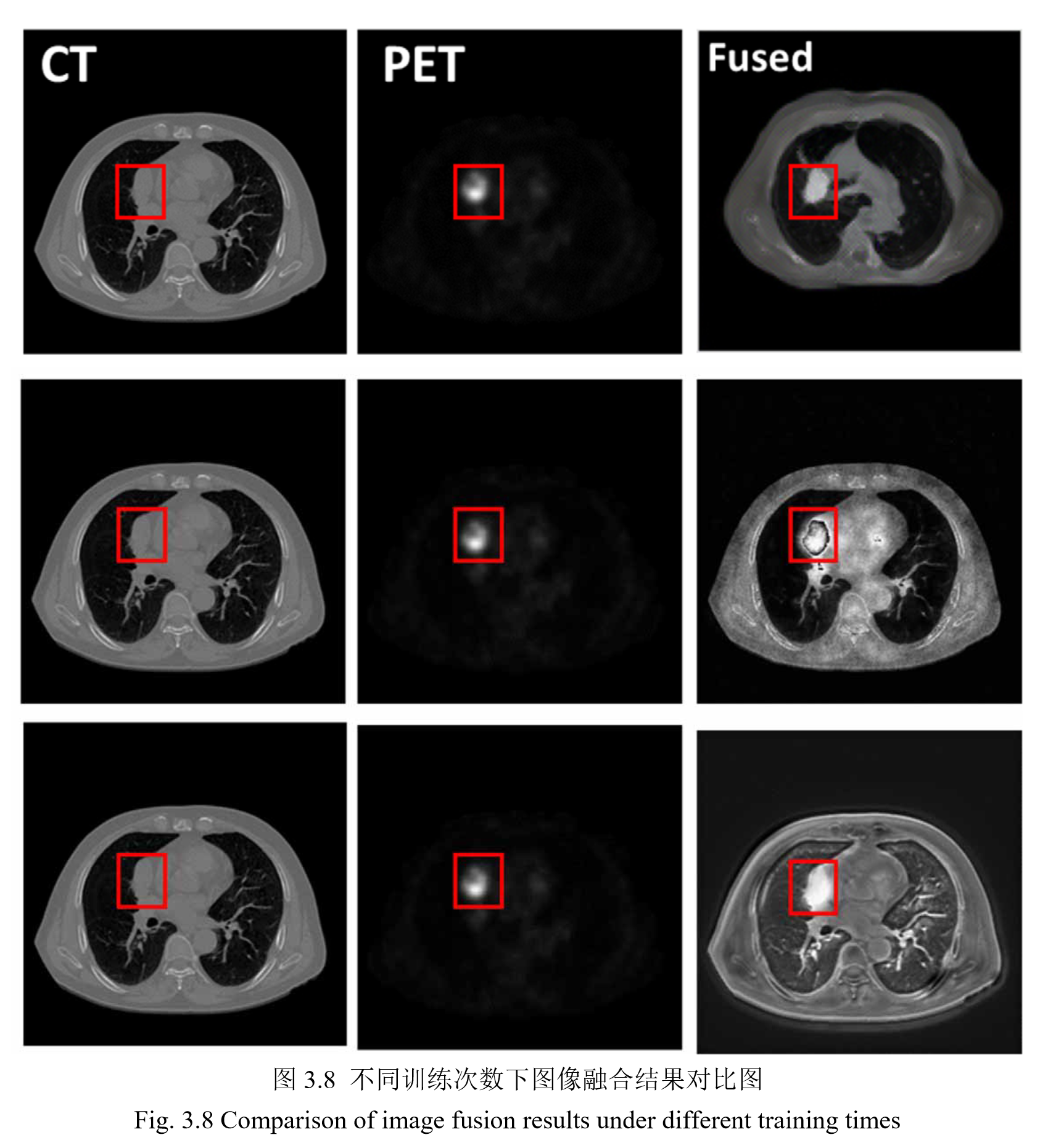
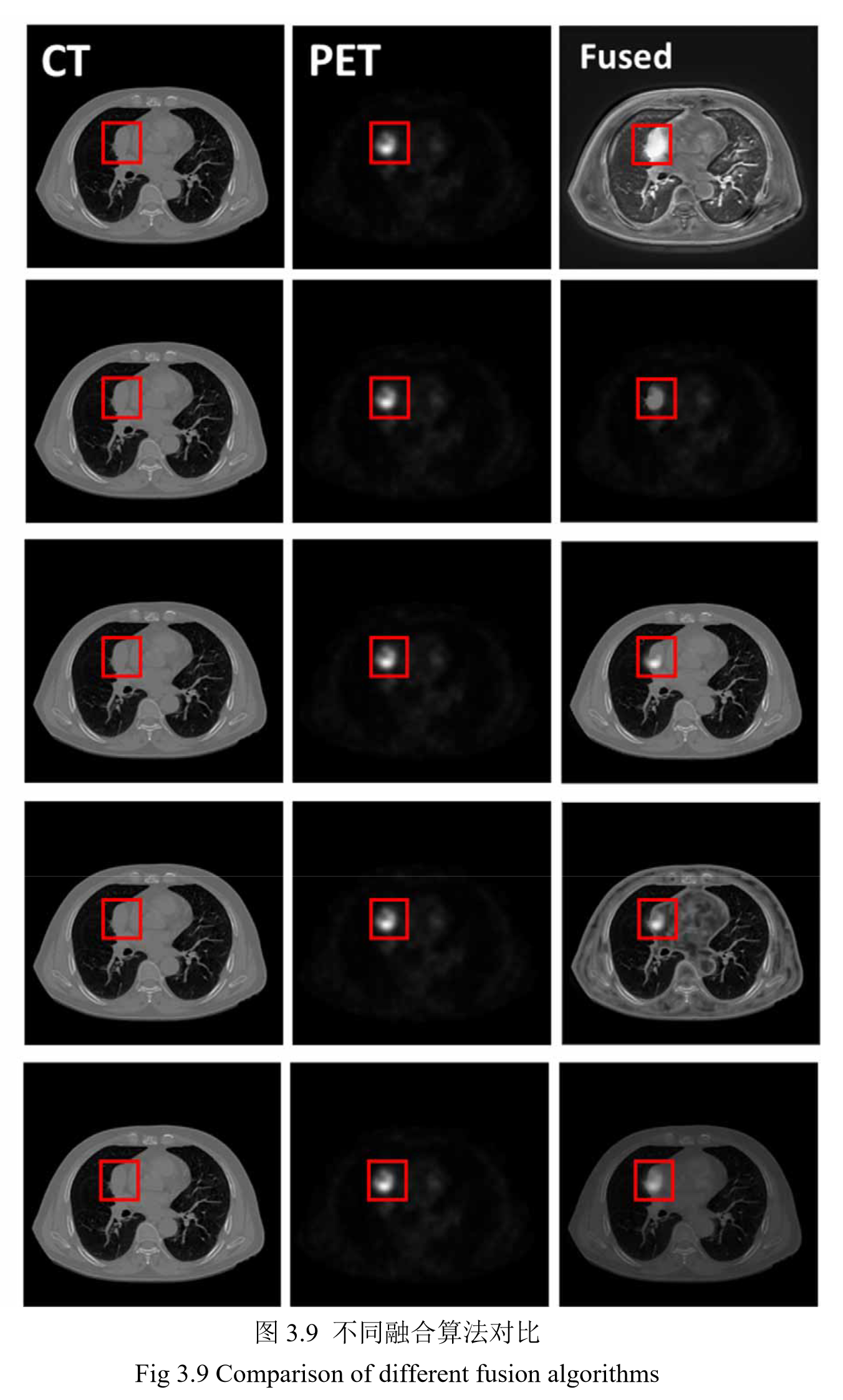
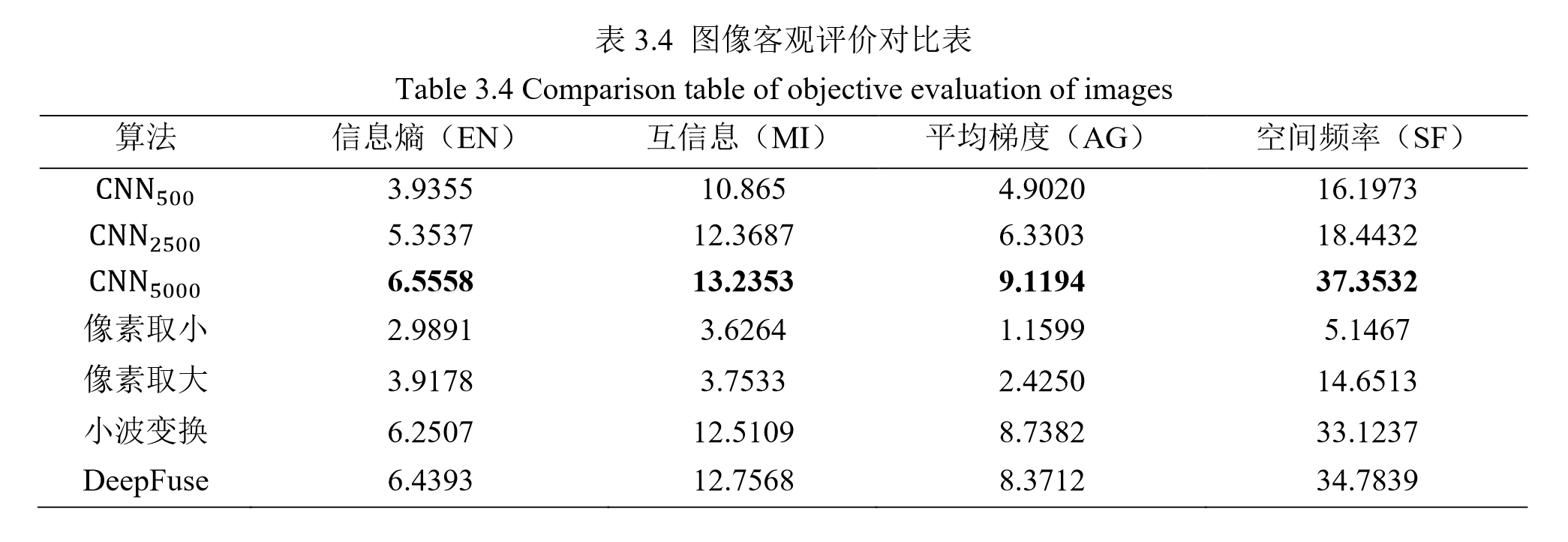
4. 基于 VGG19-GAN 的肺肿瘤图像融合
4.3 VGG19-GAN损失函数
4.3.1 Gram矩阵
n 维欧式空间中任意 k 个向量之间两两的内积所组成的矩阵,称为这 k 个向量的格拉姆矩阵(Gram matrix)
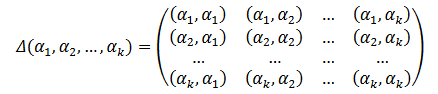
A × A T A \times A^T A×AT就是A的Gram矩阵。
Gram 矩阵是一种基于特征表示的统计方法,通常用于计算输入图像的风格信息。
对于输入图像,首先使用 CNN 提取出其在某一层的特征图(C×H×W),
Gram 矩阵的计算可以通过将该特征图重塑为一个大小为 C×H×W 的矩阵,
然后计算其转置矩阵和自身的乘积得到,
G i j = ∑ k = 1 C F i k F j k G_{ij} = \sum_{k=1}^{C} F_{ik} F_{jk} Gij=k=1∑CFikFjk
F i k F_{ik} Fik表示特征图中第i个通道的第k个像素值;
F j k F_{jk} Fjk表示特征图中第j个通道的第k个像素值;
G i j G_{ij} Gij表示第݅个通道和第݆个通道之间的相关性。
4.3.2 损失函数分析
(1)内容损失
平方误差,L2损失。
E c o n t e n t = 1 2 ∑ i = 1 n ( y i − t i ) 2 E_{content} = \frac{1}{2} \sum_{i=1}^n (y_i - t_i)^2 Econtent=21i=1∑n(yi−ti)2
(2)风格损失
Gram 矩阵实质上是不同特征之间的偏心协方差矩阵。
在每个特征层中,每个数字代表了特定位置的特定卷积核卷积所得到的结果,反映了相应特征的显著程度和两两特征之间的相关性。
对角线元素还可以表明每个特征在图像中出现的频率。
假设有两个图像ܺ和ܻ,它们的 Gram 矩阵分别为 G X G_X GX和 G Y G_Y GY。那么生成图像的风格损失函数为它们 Gram 矩阵之间的均方误差。
E s t y l e ( X , Y ) = 1 C 2 × H 2 × W 2 ∑ i = 1 C ∑ j = 1 C ∑ k = 1 H ∑ l = 1 W ( G X i , j ( k , l ) − G Y i , j ( k , l ) ) 2 E_{style}(X,Y) = \frac{1}{C^2 \times H^2 \times W^2} \sum_{i=1}^C \sum_{j=1}^C \sum_{k=1}^H \sum_{l=1}^W(G_{X_{i,j}}(k,l) - G_{Y_{i,j}}(k,l))^2 Estyle(X,Y)=C2×H2×W21i=1∑Cj=1∑Ck=1∑Hl=1∑W(GXi,j(k,l)−GYi,j(k,l))2
(3)生成图像损失
生成目标的损失函数是内容损失函数和风格损失函数的加权和。
E ( G ) = α E c o n t e n t ( C , G ) + β E s t y l e ( S , G ) E(G) = \alpha E_{content}(C,G) + \beta E_{style}(S,G) E(G)=αEcontent(C,G)+βEstyle(S,G)
C为内容图像,S为风格图像,G代表了生成图像。
4.4 VGG19-GAN激活函数
Softmax 函数,又称归一化指数函数。
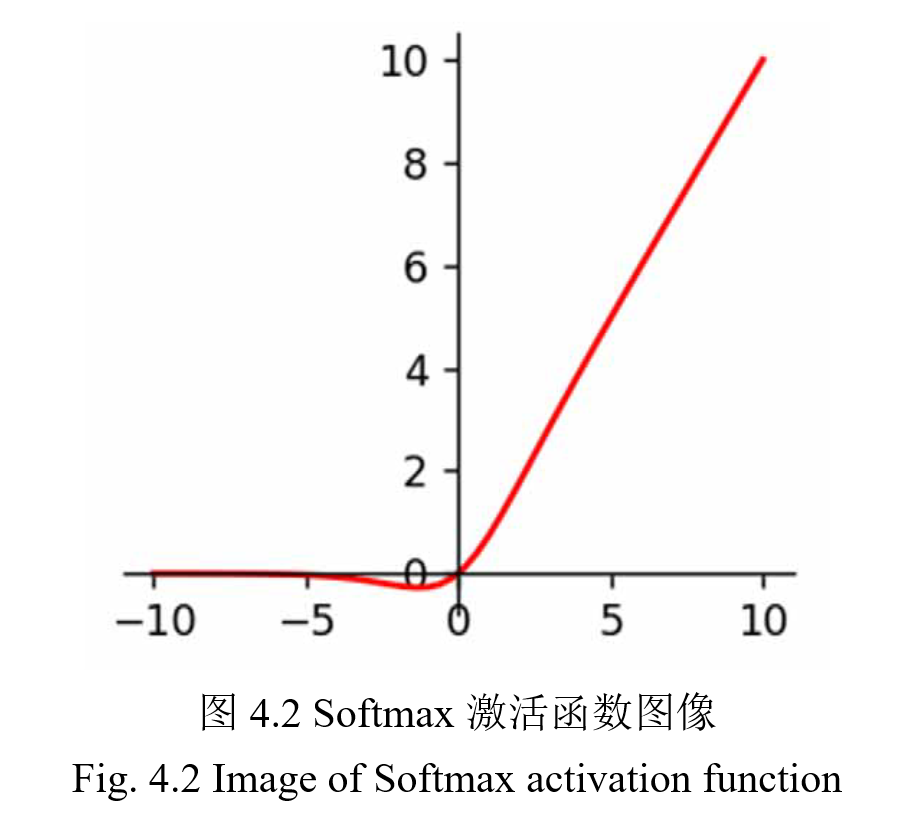
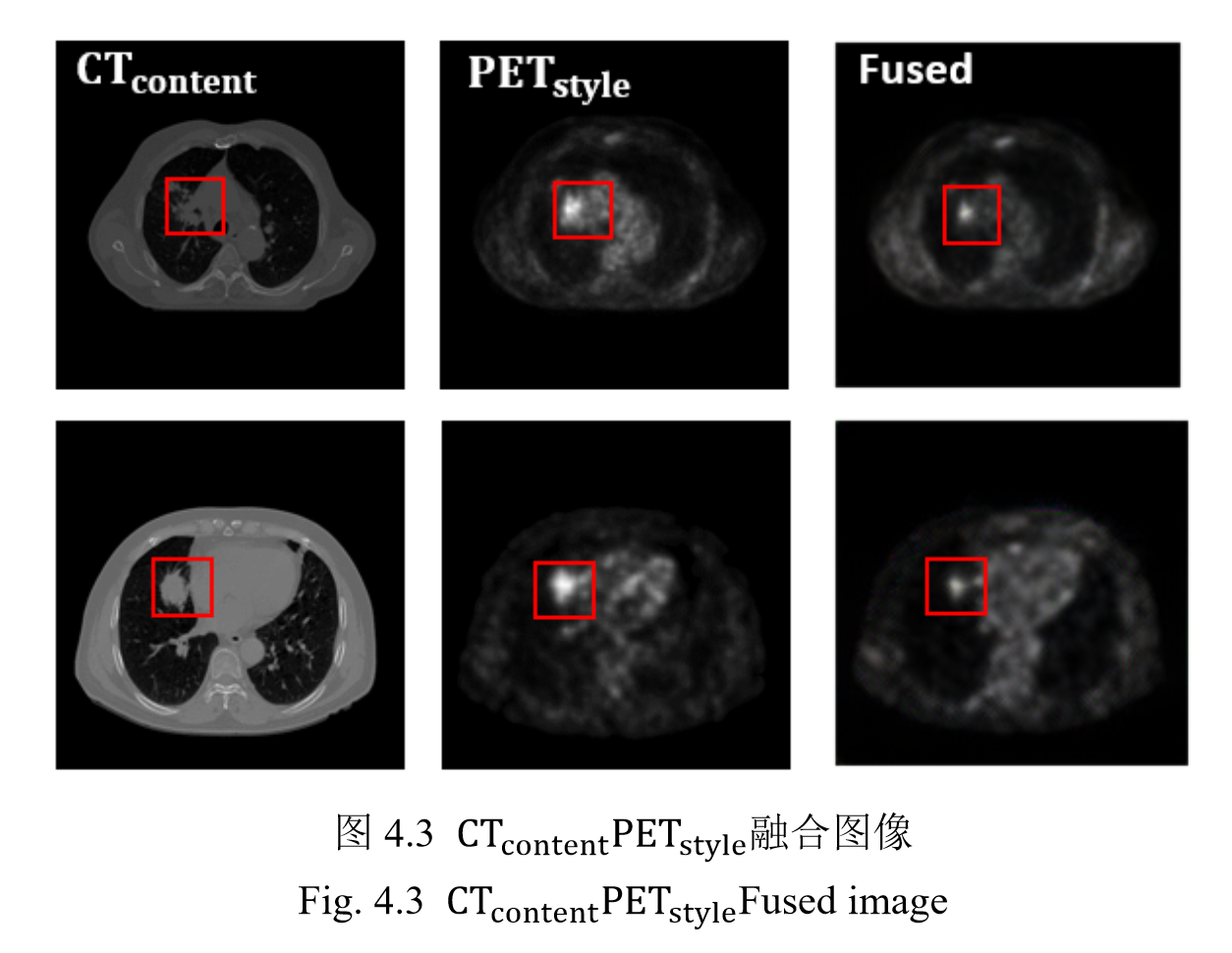
4.5 VGG19-GAN 的肺肿瘤图像融合实验
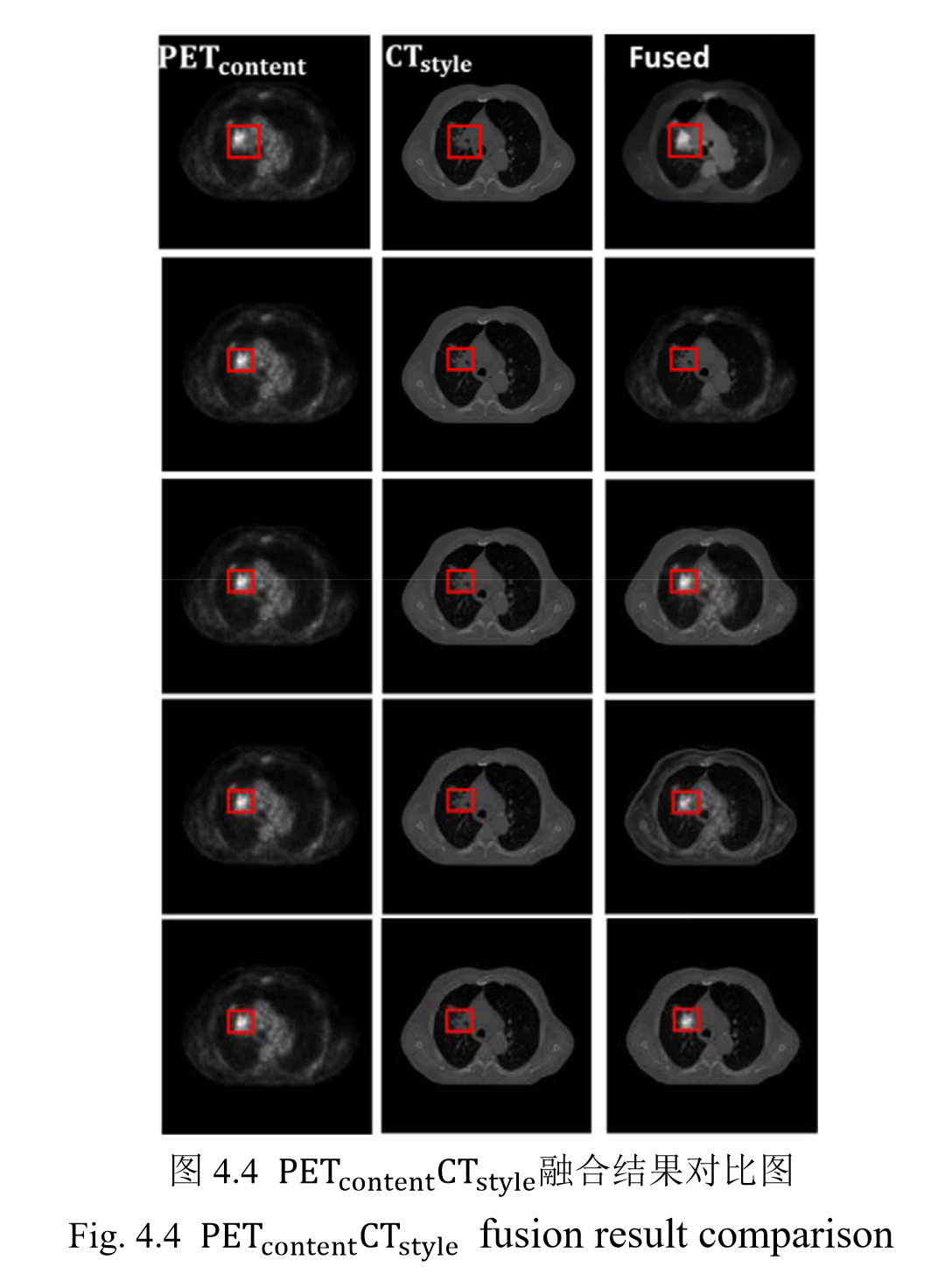
将不同模态的图像分别作为 Content 图像与 Style 图像作为输入查看融合结果, 将两个模态的输入进行互换再次查看输出结果。
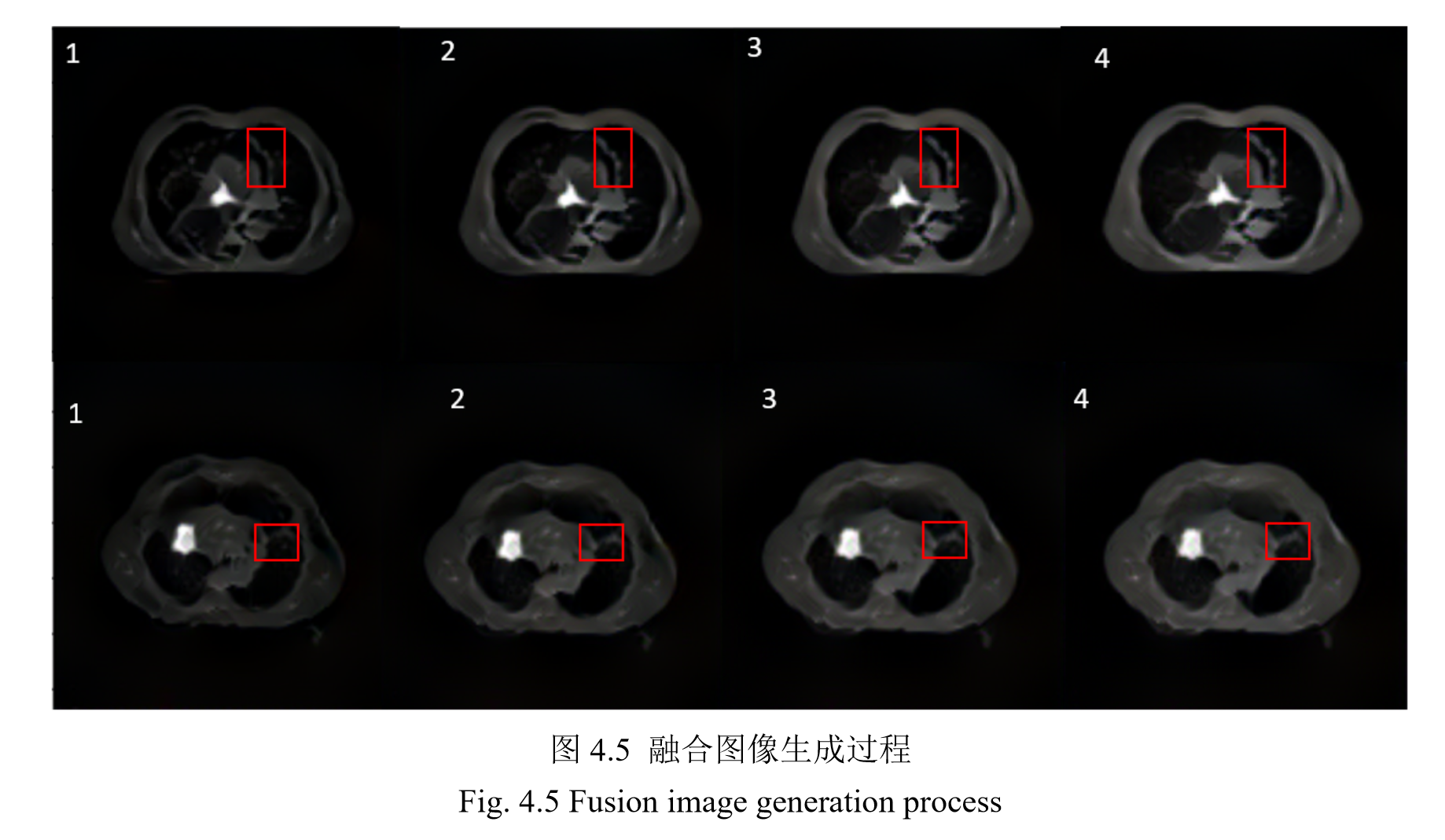
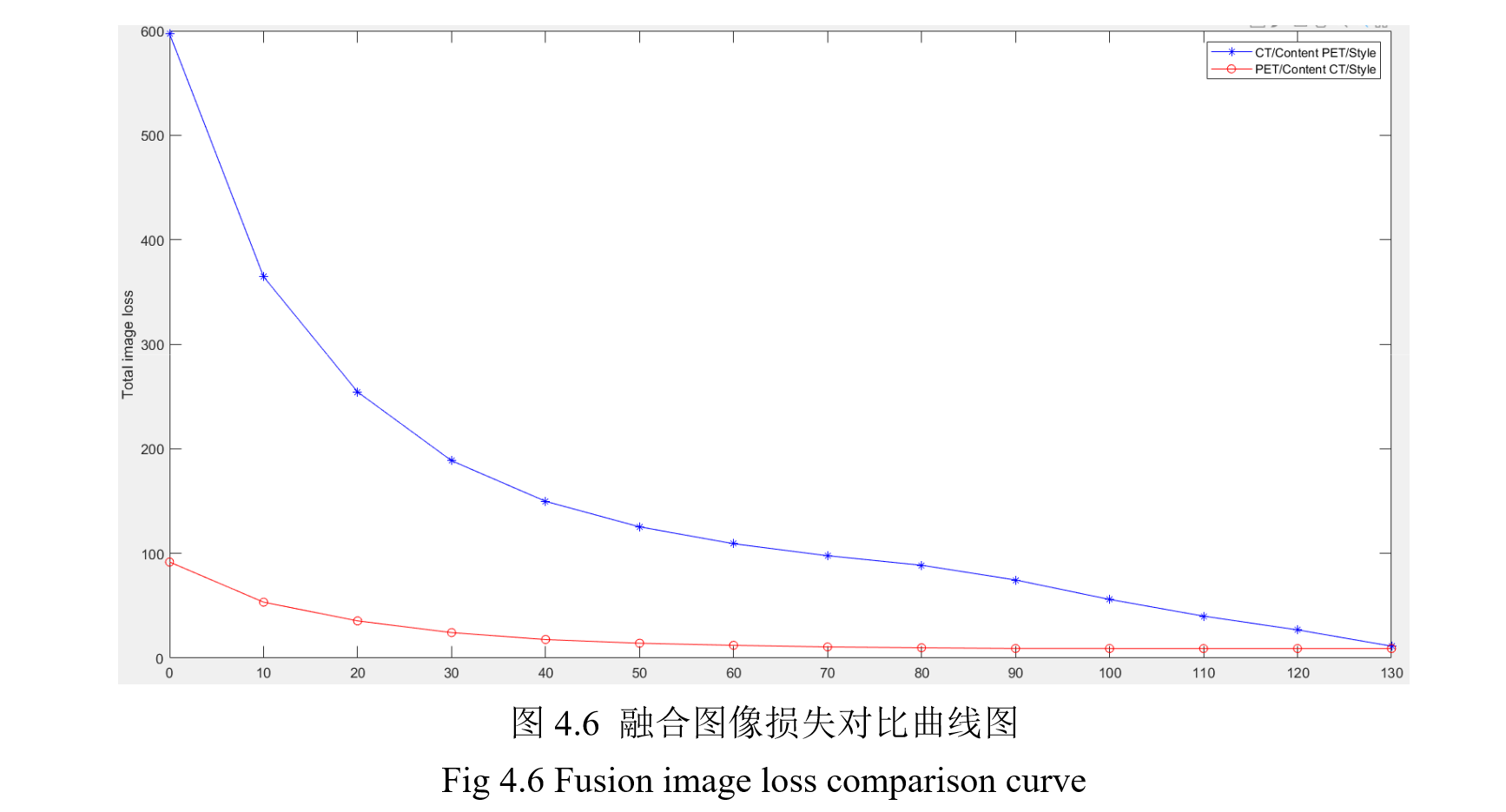
4.6 实验结果与分析