给定一个 mxn 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**
示例 1: 
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:
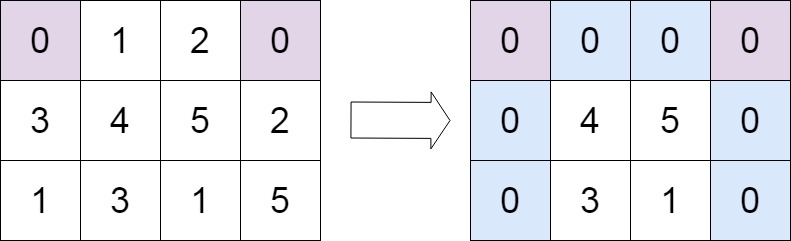
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-231 <= matrix[i][j] <= 231 - 1
进阶:
- 一个直观的解决方案是使用
O(m n)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m+n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
步骤 1:问题性质分析
该问题要求对一个 m x n 的矩阵进行修改,如果矩阵中某个元素为 0,则将其所在的整行和整列都置为 0。要求实现一个 原地(in-place)算法,即不使用额外的空间,除了常量级的辅助变量。
输入条件:
- 一个
m x n的二维矩阵matrix。 - 矩阵中每个元素的值范围在
[-231, 231 - 1]之间。 - 矩阵的大小范围是
1 <= m, n <= 200。
输出条件:
- 修改后的矩阵,其中包含
0的元素所在的行和列均被置为0。
潜在边界条件:
- 矩阵没有任何
0元素时,矩阵不变。 - 矩阵只有一行或一列时,特殊处理。
- 矩阵全为
0的情况。
步骤 2:解题思路分析
1. 直观解法:
最简单的方法是遍历整个矩阵并记录所有 0 的位置,随后再进行一次遍历,将记录的每个 0 所在的行和列都置为 0。该方法的空间复杂度是 O(m + n),时间复杂度为 O(m * n)。虽然这种方法可行,但并不符合 原地 算法的要求。
2. 进阶优化:
为了满足 原地算法 的要求,我们可以不使用额外的数组来记录 0 的位置,而是利用矩阵的第一行和第一列作为标记位置。在遍历矩阵时,如果某个元素为 0,就将该元素所在行的第一个元素和列的第一个元素设为 0,作为标记。遍历结束后,再根据这些标记,将相应的行和列置为 0。
具体步骤:
-
第一步 :先遍历矩阵,确定第一行和第一列是否需要全部置为
0。我们可以用两个布尔变量row_zero和col_zero分别标记第一行和第一列是否需要置为0。 -
第二步 :从矩阵的第二行和第二列开始遍历,遇到
0时,使用第一行和第一列的相应位置作为标记,即matrix[i][0] = 0和matrix[0][j] = 0。 -
第三步 :再从第二行和第二列开始遍历,如果
matrix[i][0] == 0或matrix[0][j] == 0,则将该行或该列置为0。 -
第四步 :最后根据
row_zero和col_zero,判断是否需要将第一行或第一列全部置为0。
算法复杂度:
- 时间复杂度 :每个元素遍历两次,时间复杂度为
O(m * n)。 - 空间复杂度 :只使用了常量级的辅助空间,空间复杂度为
O(1)。
步骤 3:详细C++代码实现


详细注释:
- 行列检测 :首先扫描第一行和第一列,判断它们是否需要最终置为
0,用row_zero和col_zero来保存这些信息。 - 使用第一行和第一列作为标记 :通过将其他行列中的
0元素信息存储到第一行和第一列,避免额外空间开销。 - 根据标记修改矩阵 :使用标记信息将相应的行和列置为
0。 - 最后处理第一行和第一列:单独处理第一行和第一列,因为它们可能会在之前的标记阶段被修改。
步骤 4:算法优化和启发
-
算法优化 :此解法通过用矩阵本身来存储标记,从而避免了额外的空间开销,是空间复杂度从
O(m + n)降低到O(1)的一种典型优化手段。 -
效率提升 :由于该算法的时间复杂度保持为
O(m * n),即遍历每个元素两次,因此即使对于最大边界情况(m, n为 200),也能在较短时间内完成。 -
处理大规模数据集的能力:这种算法适用于大规模二维矩阵的数据处理,因为它通过降低空间复杂度节省了内存资源,在实际系统中有较好的性能表现。
步骤 5:实际应用示例
在实际生活中,类似的算法可以用于处理图片处理 中的问题。例如在图片编辑软件中,如果某一部分图像像素损坏,软件可以通过将损坏的区域扩展到整个行或列来处理。这类似于将该行和列的所有像素置为 0,从而标记整个区域为无效。
另一个例子是数据挖掘中的缺失值处理 。在处理大规模数据表格时,某些列或行的关键数据缺失时,可能需要将整个行或列标记为无效数据,这个过程类似于将矩阵的整行或列置为 0 的操作。