Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解
这篇文章介绍了如何使用 Python 的 Numpy 库来实现神经网络的自动训练,重点展示了反向传播算法和激活函数的应用。反向传播是神经网络训练的核心,能够通过计算梯度来优化模型参数,使得预测更加精准。文中详细演示了如何使用 Numpy 进行神经网络的前向预测、反向传播更新、误差计算,并通过引入 ReLU 等激活函数提升模型的非线性拟合能力。最后,通过对比训练前后的结果,展示了加入激活函数后模型性能的显著提升,适合初学者和爱好者学习神经网络的基础原理与应用。
文章目录
- [Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解](#Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解)
-
-
- [一 简单介绍反向传播](#一 简单介绍反向传播)
- [二 用 Numpy 来做神经网络](#二 用 Numpy 来做神经网络)
- [三 加入激活函数](#三 加入激活函数)
- [四 完整代码示例](#四 完整代码示例)
- [五 源码地址](#五 源码地址)
-
一 简单介绍反向传播
反向传播(Backpropagation)是训练神经网络的核心算法,用于通过计算损失函数相对于网络各个参数的梯度,逐步优化这些参数,从而使模型的预测结果更加准确。使用梯度反向更新 规则做神经网络参数优化调整。
这段代码计算每一层神经层的更新幅度,让神经网络对数据拟合变好,不理解先当工具方法记住。
python
def backprop(dz, layer, layer_in, learning_rate=0.01):
"""
进行反向传播,更新当前层的权重和偏置,并计算传递给前一层的梯度。
参数:
dz: 当前层输出的梯度(损失函数对激活输出的偏导数)
layer: 当前层的参数字典,包含权重 "w" 和偏置 "b"
layer_in: 输入到当前层的激活值
learning_rate: 学习率,用于控制参数更新的步长,默认值为 0.01
返回:
new_dz: 传递给前一层的梯度
"""
# 计算损失函数对权重的梯度,layer_in.T 是当前层输入的转置,dot(dz) 进行矩阵乘法
gw = layer_in.T.dot(dz)
# 计算损失函数对偏置的梯度,按列求和,保留维度,求得每个偏置的梯度
gb = np.sum(dz, axis=0, keepdims=True)
# 计算传递给前一层的梯度,使用当前层的权重转置与 dz 相乘
new_dz = dz.dot(layer["w"].T)
# 更新当前层的权重:使用学习率乘以权重梯度,然后加到原有的权重上(梯度上升)
layer["w"] += learning_rate * gw
# 更新当前层的偏置:同样使用学习率乘以偏置梯度,然后加到原有的偏置上
layer["b"] += learning_rate * gb
# 返回传递给前一层的梯度,以便继续进行反向传播
return new_dz二 用 Numpy 来做神经网络
没有训练
python
def predict(x, l1, l2):
o1 = x.dot(l1["w"]) + l1["b"]
o2 = o1.dot(l2["w"]) + l2["b"]
return [o1, o2]
def predict01():
# 数据
x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]
y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]
# 搭建模型
l1 = layer(1, 3)
l2 = layer(3, 1)
draw_line(x, predict(x, l1, l2)[-1])
draw_scatter(x, y)运行结果
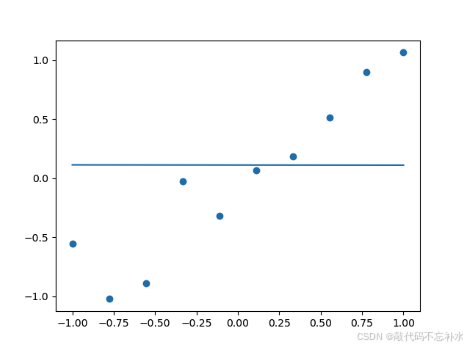
可以看出在没有训练的时候,模型预测的结果与实际 y 值在数量级上存在较大差异。
开始训练
python
def predict02():
# 数据
x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]
y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]
l1 = layer(1, 3)
l2 = layer(3, 1)
# 训练 50 次
learning_rate = 0.01
for i in range(50):
# 前向预测
o1, o2 = predict(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, o1)
_ = backprop(dz1, l1, x)
# 画一个训练后的图,对比上文中有数值问题的线
draw_line(x, predict(x, l1, l2)[-1])
draw_scatter(x, y)运行结果
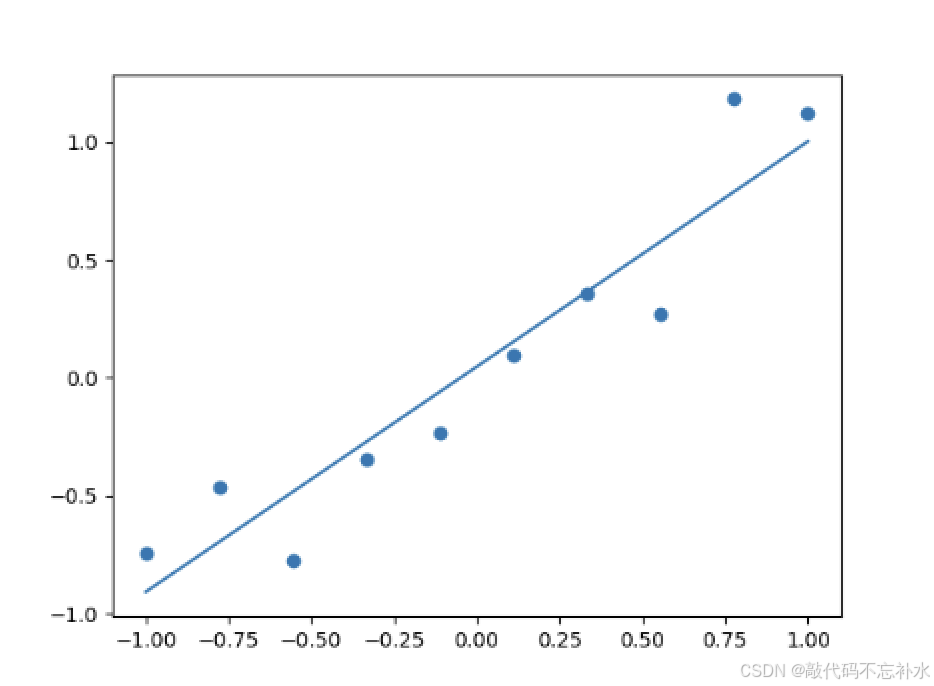
三 加入激活函数
常用激活函数
python
# 激活函数
def relu(x):
return np.maximum(0, x)
def relu_derivative(x): # 导数
return np.where(x > 0, np.ones_like(x), np.zeros_like(x))
def tanh(x):
return np.tanh(x)
def tanh_derivative(x): # 导数
return 1 - np.square(np.tanh(x))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x): # 导数
o = sigmoid(x)
return o * (1 - o)非线性计算,不加激活函数
python
def predict03():
# 非线性计算
x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]
y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]
# draw_scatter(x, y)
# 搭建模型
l1 = layer(1, 10)
l2 = layer(10, 1)
# 训练 300 次
learning_rate = 0.01
for i in range(300):
# 前向预测
o1, o2 = predict(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, o1)
_ = backprop(dz1, l1, x)
draw_line(x, predict(x, l1, l2)[-1])
draw_scatter(x, y)运行结果
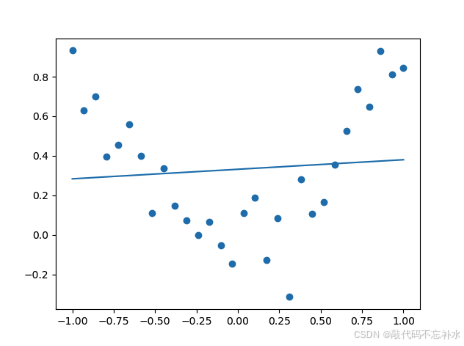
模型训练结果在量级上出现较大差距,欠拟合。
非线性计算,加入激活函数
python
def predict04():
# 非线性计算
x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]
y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]
# 搭建模型
l1 = layer(1, 10)
l2 = layer(10, 1)
# 训练 300 次
learning_rate = 0.01
for i in range(300):
# 前向预测
o1, a1, o2 = predictjihuo(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, a1)
dz1 *= relu_derivative(o1) # 这里要添加对应激活函数的反向传播
_ = backprop(dz1, l1, x)
draw_line(x, predictjihuo(x, l1, l2)[-1])
draw_scatter(x, y)运行结果
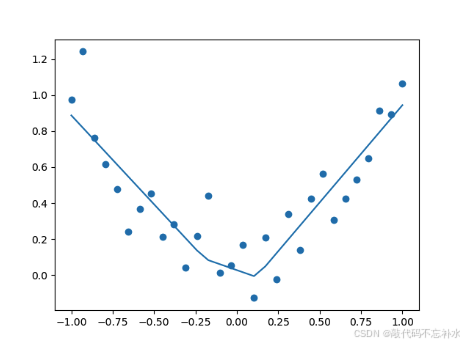
模型成功拟合了这些异常数据点,说明非线性激活函数确实非常有效。
四 完整代码示例
python
# This is a sample Python script.
from matplotlib import pyplot as plt
import numpy as np
# Press ⌃R to execute it or replace it with your code.
# Press Double ⇧ to search everywhere for classes, files, tool windows, actions, and settings.
def draw_scatter(x, y):
# 使用 matplotlib 的 scatter 方法来绘制散点图
# x.ravel() 和 y.ravel() 将 x 和 y 的二维数组转换为一维数组,适合作为散点图的输入
plt.scatter(x.ravel(), y.ravel())
# 显示图表
plt.show()
def draw_line(x, y):
idx = np.argsort(x.ravel())
plt.plot(x.ravel()[idx], y.ravel()[idx])
# plt.show()
def layer(in_dim, out_dim):
weights = np.random.normal(loc=0, scale=0.1, size=[in_dim, out_dim])
bias = np.full([1, out_dim], 0.1)
return {"w": weights, "b": bias}
# 激活函数
def relu(x):
return np.maximum(0, x)
def relu_derivative(x): # 导数
return np.where(x > 0, np.ones_like(x), np.zeros_like(x))
def tanh(x):
return np.tanh(x)
def tanh_derivative(x): # 导数
return 1 - np.square(np.tanh(x))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x): # 导数
o = sigmoid(x)
return o * (1 - o)
def backprop(dz, layer, layer_in, learning_rate=0.01):
"""
进行反向传播,更新当前层的权重和偏置,并计算传递给前一层的梯度。
参数:
dz: 当前层输出的梯度(损失函数对激活输出的偏导数)
layer: 当前层的参数字典,包含权重 "w" 和偏置 "b"
layer_in: 输入到当前层的激活值
learning_rate: 学习率,用于控制参数更新的步长,默认值为 0.01
返回:
new_dz: 传递给前一层的梯度
"""
# 计算损失函数对权重的梯度,layer_in.T 是当前层输入的转置,dot(dz) 进行矩阵乘法
gw = layer_in.T.dot(dz)
# 计算损失函数对偏置的梯度,按列求和,保留维度,求得每个偏置的梯度
gb = np.sum(dz, axis=0, keepdims=True)
# 计算传递给前一层的梯度,使用当前层的权重转置与 dz 相乘
new_dz = dz.dot(layer["w"].T)
# 更新当前层的权重:使用学习率乘以权重梯度,然后加到原有的权重上(梯度上升)
layer["w"] += learning_rate * gw
# 更新当前层的偏置:同样使用学习率乘以偏置梯度,然后加到原有的偏置上
layer["b"] += learning_rate * gb
# 返回传递给前一层的梯度,以便继续进行反向传播
return new_dz
def predictjihuo(x, l1, l2):
o1 = x.dot(l1["w"]) + l1["b"]
a1 = relu(o1) # 这里我添加了一个激活函数
o2 = a1.dot(l2["w"]) + l2["b"]
return [o1, a1, o2]
def predict(x, l1, l2):
"""
预测函数,执行前向传播,计算两层神经网络的输出。
参数:
x: 输入数据,形状为 [N, 输入特征数],此处为 [10, 1]。
l1: 第一层的参数字典,包含权重 "w" 和偏置 "b"。
l2: 第二层的参数字典,包含权重 "w" 和偏置 "b"。
返回:
o1: 第一层的输出结果。
o2: 第二层的输出结果(最终输出)。
"""
# 第一层的输出,x.dot(l1["w"]) 是线性组合,+ l1["b"] 加上偏置
o1 = x.dot(l1["w"]) + l1["b"]
# 第二层的输出,o1.dot(l2["w"]) 是线性组合,+ l2["b"] 加上偏置
o2 = o1.dot(l2["w"]) + l2["b"]
# 返回两层的输出,o1 为第一层的输出,o2 为最终的输出
return [o1, o2]
def predict01():
"""
模拟预测和数据绘制函数,包含数据生成、模型搭建、前向预测和绘图。
"""
# 生成输入数据 x,使用 np.linspace 生成从 -1 到 1 的 10 个均匀分布的点,并reshape为 [10, 1]
x = np.linspace(-1, 1, 10)[:, None] # 形状 [10, 1]
# 生成目标值 y,基于 x 加上高斯噪声,模拟真实数据,形状为 [10, 1]
y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # 形状 [10, 1]
# 搭建神经网络模型
# 第一层:输入维度为 1,输出维度为 3(即3个神经元)
l1 = layer(1, 3)
# 第二层:输入维度为 3,输出维度为 1
l2 = layer(3, 1)
# 使用 predict 函数进行前向传播,绘制预测结果
# 只提取第二层的输出 o2 来绘制预测的线
draw_line(x, predict(x, l1, l2)[-1])
# 绘制真实数据点的散点图
draw_scatter(x, y)
def predict02():
# 数据
x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]
y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]
l1 = layer(1, 3)
l2 = layer(3, 1)
# 训练 50 次
learning_rate = 0.01
for i in range(50):
# 前向预测
o1, o2 = predict(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, o1)
_ = backprop(dz1, l1, x)
# 画一个训练后的图,对比上文中有数值问题的线
draw_line(x, predict(x, l1, l2)[-1])
draw_scatter(x, y)
def predict03():
# 非线性计算
x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]
y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]
# draw_scatter(x, y)
# 搭建模型
l1 = layer(1, 10)
l2 = layer(10, 1)
# 训练 300 次
learning_rate = 0.01
for i in range(300):
# 前向预测
o1, o2 = predict(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, o1)
_ = backprop(dz1, l1, x)
draw_line(x, predict(x, l1, l2)[-1])
draw_scatter(x, y)
def predict04():
# 非线性计算
x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]
y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]
# 搭建模型
l1 = layer(1, 10)
l2 = layer(10, 1)
# 训练 300 次
learning_rate = 0.01
for i in range(300):
# 前向预测
o1, a1, o2 = predictjihuo(x, l1, l2)
# 误差计算
if i % 10 == 0:
average_cost = np.mean(np.square(o2 - y))
print(average_cost)
# 反向传播,梯度更新
dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数
dz1 = backprop(dz2, l2, a1)
dz1 *= relu_derivative(o1) # 这里要添加对应激活函数的反向传播
_ = backprop(dz1, l1, x)
draw_line(x, predictjihuo(x, l1, l2)[-1])
draw_scatter(x, y)
def print_hi(name):
# Use a breakpoint in the code line below to debug your script.
print(f'Hi, {name}') # Press ⌘F8 to toggle the breakpoint.
# 模型前向预测
# 数据
x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]
y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]
# draw_scatter(x, y)
# 模型
l1 = layer(1, 3)
l2 = layer(3, 1)
# 计算
o = x.dot(l1["w"]) + l1["b"]
print("第一层出来后的 shape:", o.shape)
o = o.dot(l2["w"]) + l2["b"]
print("第二层出来后的 shape:", o.shape)
print("output:", o)
# draw_scatter(x, o)
# 简单介绍反向传播
# predict01()
# predict02()
# 加入激活函数
# 非线性计算,没有激活函数的网络训练,量级上的差距大
# predict03()
# 非线性计算,加入激活函数
predict04()
# Press the green button in the gutter to run the script.
if __name__ == '__main__':
print_hi('神经网络-自动训练')
# See PyCharm help at https://www.jetbrains.com/help/pycharm/复制粘贴并覆盖到你的 main.py 中运行,运行结果如下。
lua
Hi, 神经网络-自动训练
第一层出来后的 shape: (10, 3)
第二层出来后的 shape: (10, 1)
output: [[0.08015376]
[0.08221984]
[0.08428592]
[0.086352 ]
[0.08841808]
[0.09048416]
[0.09255024]
[0.09461632]
[0.0966824 ]
[0.09874848]]
0.2226335913018929
0.18084056623965614
0.17646520657891238
0.16955062165383475
0.15974897747454914
0.14609449775016456
0.12879398035319886
0.11000871768876343
0.09272999949822598
0.07986100731357502
0.07149628207512877
0.06657668787644673
0.06412748050655417
0.06308965708664192
0.06255298788129363
0.06233764319523034
0.06229224784095634
0.062220235356859256
0.06227320308423159
0.06227607241875045
0.06218961938206315
0.062183519685144004
0.06220136162617964
0.062260925337883535
0.06228186644083771
0.062212564435570314
0.06214763225225857
0.062190709318072676
0.06225667345334308
0.06227302776778138五 源码地址
代码地址:
国内看 Gitee 之 numpy/神经网络-自动训练.py
国外看 GitHub 之 numpy/神经网络-自动训练.py
引用 莫烦 Python