BCE Loss
交叉熵损失函数计算公式:
BCE Loss = - 1/n*(y_actual * log(y_pred) + (1 - y_actual) * log(1 - y_pred))
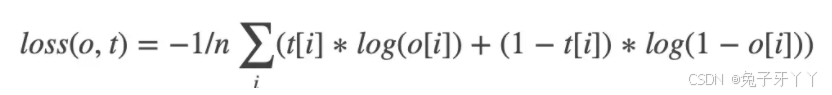
t[i]为标签值:0或者1
o[i]是经过sigmoid后的概率值
BCEWithLogitsLoss
这个损失将Sigmoid层和BCELoss合并在一个类中。
BCEWithLogitsLoss`(weight=None, size_average=None, reduce=None, reduction='mean', pos_weight=None)
python
import torch
from torch import autograd
input = autograd.Variable(torch.tensor([[ 1.9072, 1.1079, 1.4906],
[-0.6584, -0.0512, 0.7608],
[-0.0614, 0.6583, 0.1095]]), requires_grad=True)
print(input)
print('-'*100)
from torch import nn
m = nn.Sigmoid()
print(m(input))
print('-'*100)
target = torch.FloatTensor([[0, 1, 1], [1, 1, 1], [0, 0, 0]])
print(target)
print('-'*100)
import math
r11 = 0 * math.log(0.8707) + (1-0) * math.log((1 - 0.8707))
r12 = 1 * math.log(0.7517) + (1-1) * math.log((1 - 0.7517))
r13 = 1 * math.log(0.8162) + (1-1) * math.log((1 - 0.8162))
r21 = 1 * math.log(0.3411) + (1-1) * math.log((1 - 0.3411))
r22 = 1 * math.log(0.4872) + (1-1) * math.log((1 - 0.4872))
r23 = 1 * math.log(0.6815) + (1-1) * math.log((1 - 0.6815))
r31 = 0 * math.log(0.4847) + (1-0) * math.log((1 - 0.4847))
r32 = 0 * math.log(0.6589) + (1-0) * math.log((1 - 0.6589))
r33 = 0 * math.log(0.5273) + (1-0) * math.log((1 - 0.5273))
r1 = -(r11 + r12 + r13) / 3
#0.8447112733378236
r2 = -(r21 + r22 + r23) / 3
#0.7260397266631787
r3 = -(r31 + r32 + r33) / 3
#0.8292933181294807
bceloss = (r1 + r2 + r3) / 3
print(bceloss)
print('-'*100)
loss = nn.BCELoss()
print(loss(m(input), target))
print('-'*100)
loss = nn.BCEWithLogitsLoss()
print(loss(input, target))结果
原始的3x3矩阵:
tensor([[ 1.9072, 1.1079, 1.4906],
-0.6584, -0.0512, 0.7608\],
\[-0.0614, 0.6583, 0.1095\]\], requires_grad=True)
----------------------------------------------------------------------------------------------------
### 使用Sigmoid矩阵进行计算:
tensor(\[\[0.8707, 0.7517, 0.8162\],
\[0.3411, 0.4872, 0.6815\],
\[0.4847, 0.6589, 0.5273\]\], grad_fn=\