深度学习实战（基于pytroch）系列（四十二）双向循环神经网络pytorch实现

双向循环神经网络pytorch实现

架构概述

传统循环神经网络假设当前时间步的状态仅由历史信息决定，信息单向从前往后传递。然而在实际应用中，当前时间步可能受到未来信息的影响。例如，在自然语言处理中，理解一个词的含义往往需要结合其上下文信息。双向循环神经网络通过引入反向传播路径，能够同时利用过去和未来的上下文信息。

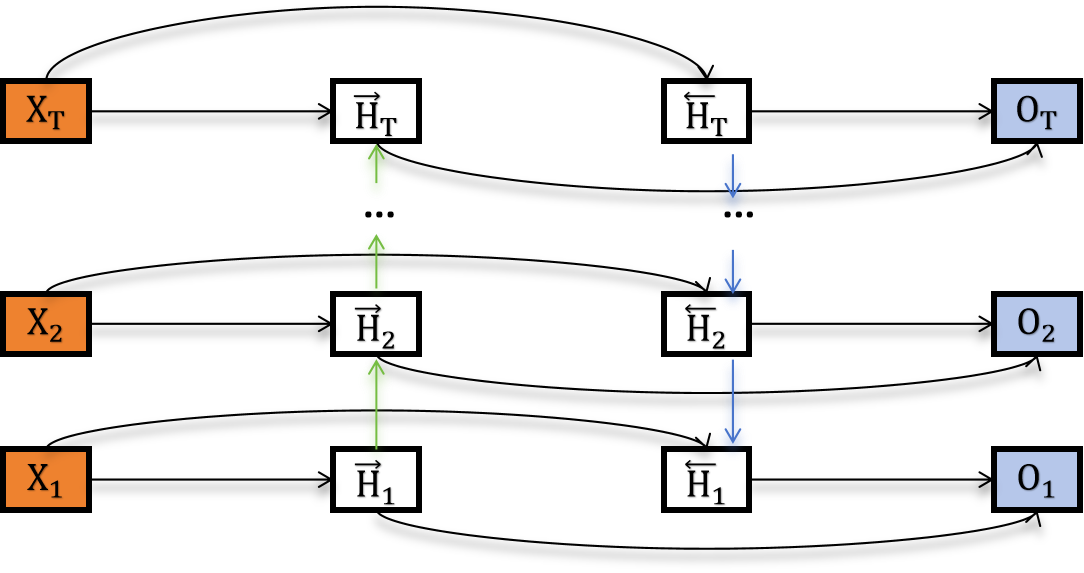
上图展示了一个单隐藏层的双向循环神经网络架构，包含正向和反向两个传播方向。

数学定义

给定时间步 t t t 的小批量输入 X t ∈ R n × d \boldsymbol{X}_t \in \mathbb{R}^{n \times d} Xt∈Rn×d（其中 n n n 为样本数， d d d 为输入维度），以及隐藏层激活函数 ϕ \phi ϕ。在双向循环神经网络中：

正向隐藏状态 ： H → t ∈ R n × h \overrightarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h} H t∈Rn×h（正向隐藏单元个数为 h h h）
反向隐藏状态 ： H ← t ∈ R n × h \overleftarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h} H t∈Rn×h（反向隐藏单元个数为 h h h）

两个方向的隐藏状态分别计算如下：

H → t = ϕ ( X t W x h ( f ) + H → t − 1 W h h ( f ) + b h ( f ) ) , H ← t = ϕ ( X t W x h ( b ) + H ← t + 1 W h h ( b ) + b h ( b ) ) , \begin{aligned} \overrightarrow{\boldsymbol{H}}t &= \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}{t-1} \boldsymbol{W}_{hh}^{(f)} + \boldsymbol{b}h^{(f)}),\\ \overleftarrow{\boldsymbol{H}}t &= \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}{t+1} \boldsymbol{W}{hh}^{(b)} + \boldsymbol{b}_h^{(b)}), \end{aligned} H tH t=ϕ(XtWxh(f)+H t−1Whh(f)+bh(f)),=ϕ(XtWxh(b)+H t+1Whh(b)+bh(b)),

其中模型参数包括：

权重矩阵 ：
- W x h ( f ) ∈ R d × h \boldsymbol{W}_{xh}^{(f)} \in \mathbb{R}^{d \times h} Wxh(f)∈Rd×h（正向输入到隐藏层）
- W h h ( f ) ∈ R h × h \boldsymbol{W}_{hh}^{(f)} \in \mathbb{R}^{h \times h} Whh(f)∈Rh×h（正向隐藏层到隐藏层）
- W x h ( b ) ∈ R d × h \boldsymbol{W}_{xh}^{(b)} \in \mathbb{R}^{d \times h} Wxh(b)∈Rd×h（反向输入到隐藏层）
- W h h ( b ) ∈ R h × h \boldsymbol{W}_{hh}^{(b)} \in \mathbb{R}^{h \times h} Whh(b)∈Rh×h（反向隐藏层到隐藏层）
偏置向量 ：
- b h ( f ) ∈ R 1 × h \boldsymbol{b}_h^{(f)} \in \mathbb{R}^{1 \times h} bh(f)∈R1×h（正向隐藏层偏置）
- b h ( b ) ∈ R 1 × h \boldsymbol{b}_h^{(b)} \in \mathbb{R}^{1 \times h} bh(b)∈R1×h（反向隐藏层偏置）

输出计算

将两个方向的隐藏状态进行拼接，得到完整的隐藏状态表示：

H t = [ H → t , H ← t ] ∈ R n × 2 h \boldsymbol{H}_t = [\overrightarrow{\boldsymbol{H}}_t, \overleftarrow{\boldsymbol{H}}_t] \in \mathbb{R}^{n \times 2h} Ht=[H t,H t]∈Rn×2h

输出层基于拼接后的隐藏状态计算最终输出：

O t = H t W h q + b q , \boldsymbol{O}_t = \boldsymbol{H}t \boldsymbol{W}{hq} + \boldsymbol{b}_q, Ot=HtWhq+bq,

其中输出层参数包括：

W h q ∈ R 2 h × q \boldsymbol{W}_{hq} \in \mathbb{R}^{2h \times q} Whq∈R2h×q（隐藏层到输出层的权重矩阵）
b q ∈ R 1 × q \boldsymbol{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q（输出层偏置向量）
q q q 为输出维度

扩展说明

非对称架构 ：正向和反向的隐藏单元个数可以不同，即 H → t ∈ R n × h f \overrightarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h_f} H t∈Rn×hf， H ← t ∈ R n × h b \overleftarrow{\boldsymbol{H}}_t \in \mathbb{R}^{n \times h_b} H t∈Rn×hb，此时 H t ∈ R n × ( h f + h b ) \boldsymbol{H}_t \in \mathbb{R}^{n \times (h_f + h_b)} Ht∈Rn×(hf+hb)
多层扩展：可以通过堆叠多个双向循环神经网络层来构建深层架构，每一层的输出作为下一层的输入
初始化策略 ：正向序列的初始隐藏状态 H → 0 \overrightarrow{\boldsymbol{H}}0 H 0 和反向序列的初始隐藏状态 H ← T + 1 \overleftarrow{\boldsymbol{H}}{T+1} H T+1（ T T T 为序列长度）通常初始化为零向量或可学习的参数

实现

这里我们使用PyTorch内置RNN来实现双向循环网络，其中input_size代表输入特征维度，hidden_size代表隐藏层单元数 (每个方向)，output_size代表输出维度，num_layers代表RNN层数，nonlinearity代表激活函数以及dropout代表Dropout概率。

python 复制代码

class BiRNNSimple(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_layers=1, 
                 nonlinearity='tanh', dropout=0.0):
        """
        使用PyTorch内置RNN实现的双向循环神经网络
        """
        super(BiRNNSimple, self).__init__()
        
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=num_layers,
            batch_first=False,  # (seq_len, batch, input_size)
            bidirectional=True,
            nonlinearity=nonlinearity,
            dropout=dropout
        )
        
        # 输出层
        self.fc = nn.Linear(hidden_size * 2, output_size)
    
    def forward(self, x):
        """
        Args:
            x: (seq_len, batch_size, input_size)
            
        Returns:
            output: (seq_len, batch_size, output_size)
        """
        # RNN前向传播
        rnn_output, _ = self.rnn(x)  # (seq_len, batch_size, 2*hidden_size)
        
        # 全连接层
        output = self.fc(rnn_output)  # (seq_len, batch_size, output_size)
        
        return output

对上面代码进行测试

python 复制代码

def test_birnn():
    # 参数设置
    input_size = 10
    hidden_size = 16
    output_size = 5
    batch_size = 4
    seq_len = 6
    
    # 创建模型
    model_custom = BiRNN(input_size, hidden_size, output_size)
    model_simple = BiRNNSimple(input_size, hidden_size, output_size)
    
    # 创建测试数据
    X = torch.randn(seq_len, batch_size, input_size)
    
    # 测试自定义模型
    output_custom = model_custom(X)
    print(f"Custom BiRNN output shape: {output_custom.shape}")
    
    # 测试简化模型
    output_simple = model_simple(X)
    print(f"Simple BiRNN output shape: {output_simple.shape}")
    
    # 验证输出形状
    assert output_custom.shape == (seq_len, batch_size, output_size)
    assert output_simple.shape == (seq_len, batch_size, output_size)
    
    print("All tests passed!")


if __name__ == "__main__":
    test_birnn()

小结

双向循环神经网络在每个时间步的隐藏状态同时编码了该时间步之前和之后的序列信息
通过结合正向和反向的上下文信息，能够更全面地理解序列数据的特征
特别适用于需要全局上下文信息的任务，如机器翻译、语音识别、命名实体识别等

本系列目录链接