
文章目录
- 1.排序的概念
- [2. 插入排序](#2. 插入排序)
-
- [2.1 基本思想](#2.1 基本思想)
- [2.2 插入排序的实现](#2.2 插入排序的实现)
- [2.3 优缺点分析](#2.3 优缺点分析)
- [3. 希尔排序](#3. 希尔排序)
-
- [3.1 基本思想和排序的实现](#3.1 基本思想和排序的实现)
- [3.2 gap的值](#3.2 gap的值)
- [3.3 优缺点分析](#3.3 优缺点分析)
1.排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
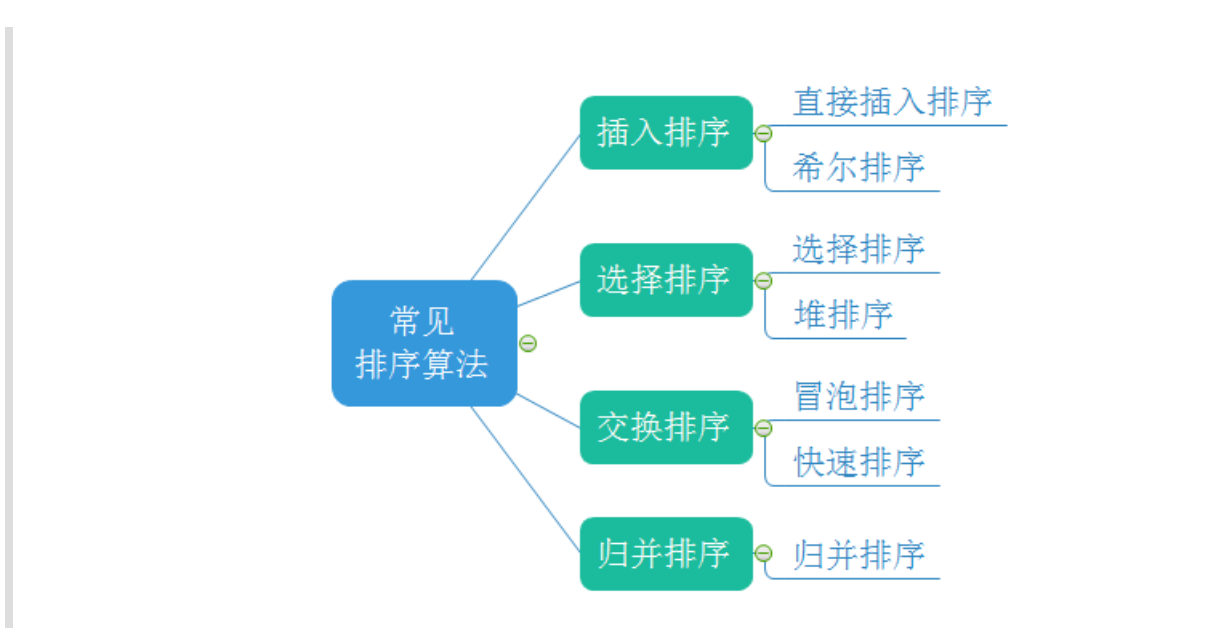
常用的排序如下:
2. 插入排序
2.1 基本思想
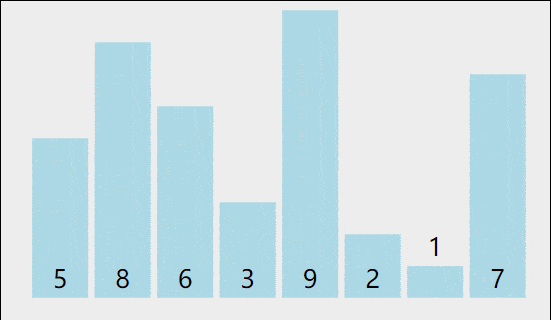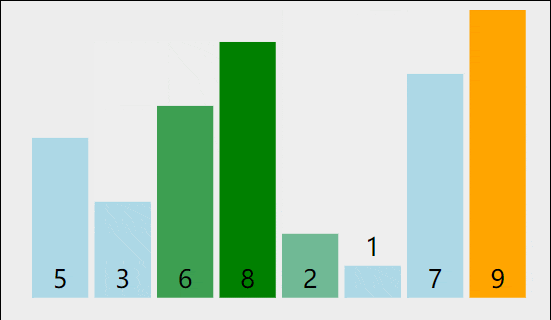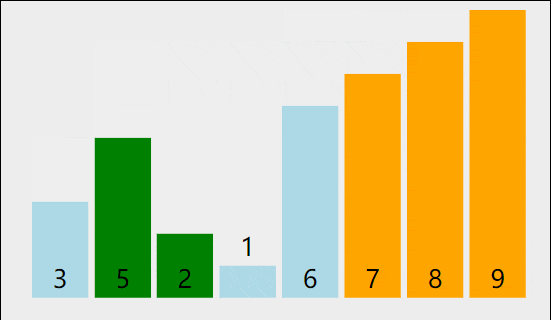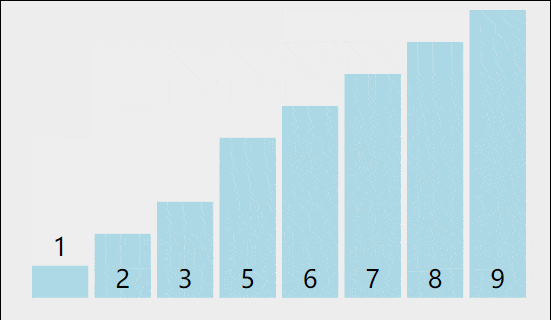
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为 止,得到一个新的有序序列 。
先来看一下图解:
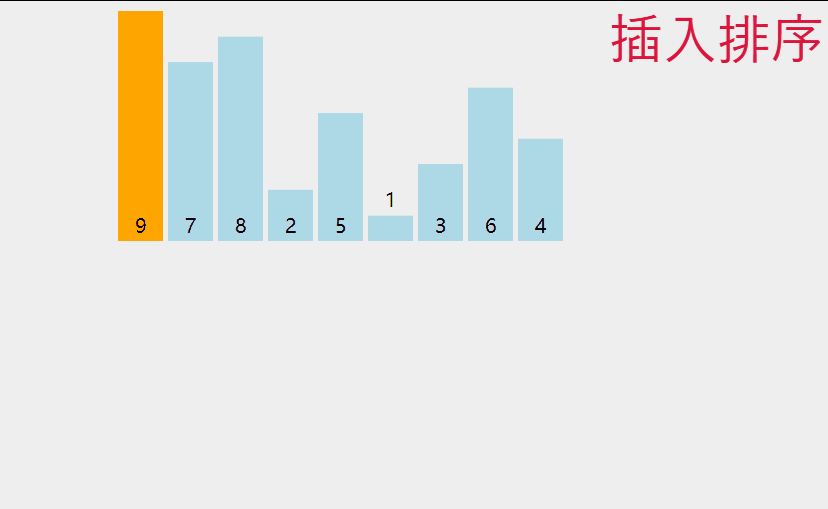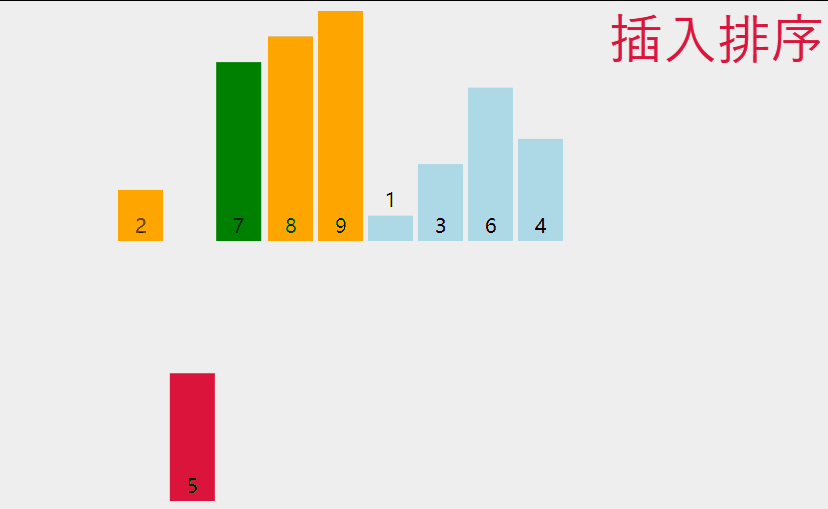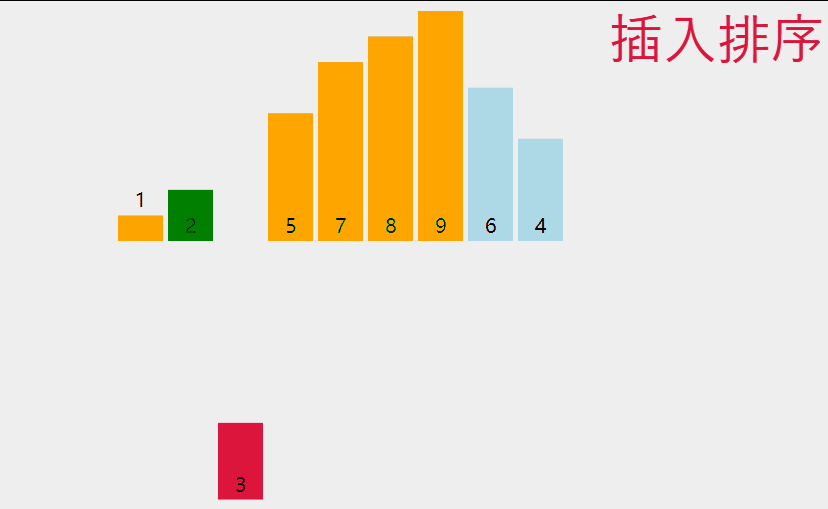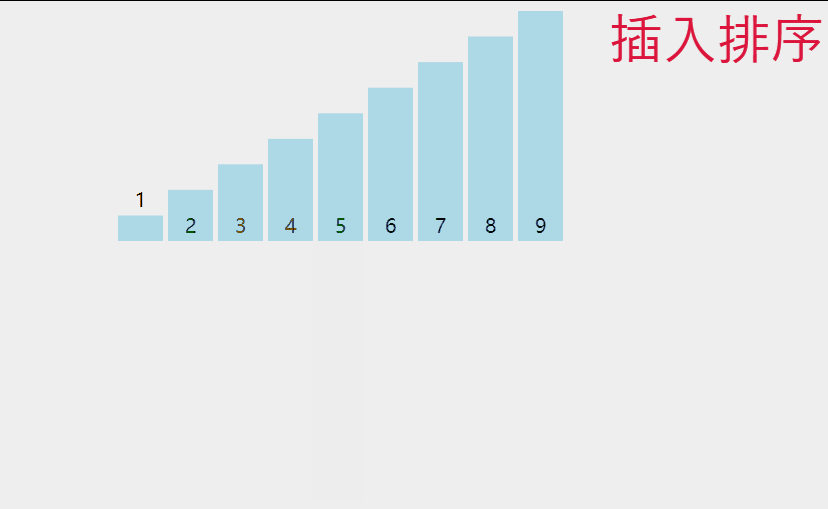
其实就是将选中的数,将其插入到其中,让其前面有序
和之前冒泡排序的区别:
2.2 插入排序的实现
单趟排序实现:
cpp
int end;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;再将趟数补全,注意不要访问越界
cpp
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++) //为了放置后面end+1访问越界
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
2.3 优缺点分析
时间复杂度为:O(N^2)
逆序的时候时间最长
顺序的时候为时间最短 此时复杂度为O(N)
这里我们写一段测试时间的代码:
cpp
void TestOP()
{
srand(time(0));
const int N = 1000000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand() + i;
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
int begin1 = clock();
//InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
//HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
//QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
//MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
//BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("QuickSort:%d\n", end5 - begin5);
printf("MergeSort:%d\n", end6 - begin6);
printf("BubbleSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
}再将冒泡排序和堆排序的代码拿过来进行对比
cpp
//堆排序
void AdjustDown(int* a, int n, int parent)
{
// 先假设左孩子小
int child = parent * 2 + 1;
while (child < n) // child >= n说明孩子不存在,调整到叶子了
{
// 找出小的那个孩子
if (child + 1 < n && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n)
{
// 向下调整建堆 O(N)
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
// 单趟
int flag = 0;
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
flag = 1;
}
}
if (flag == 0)
{
break;
}
}
}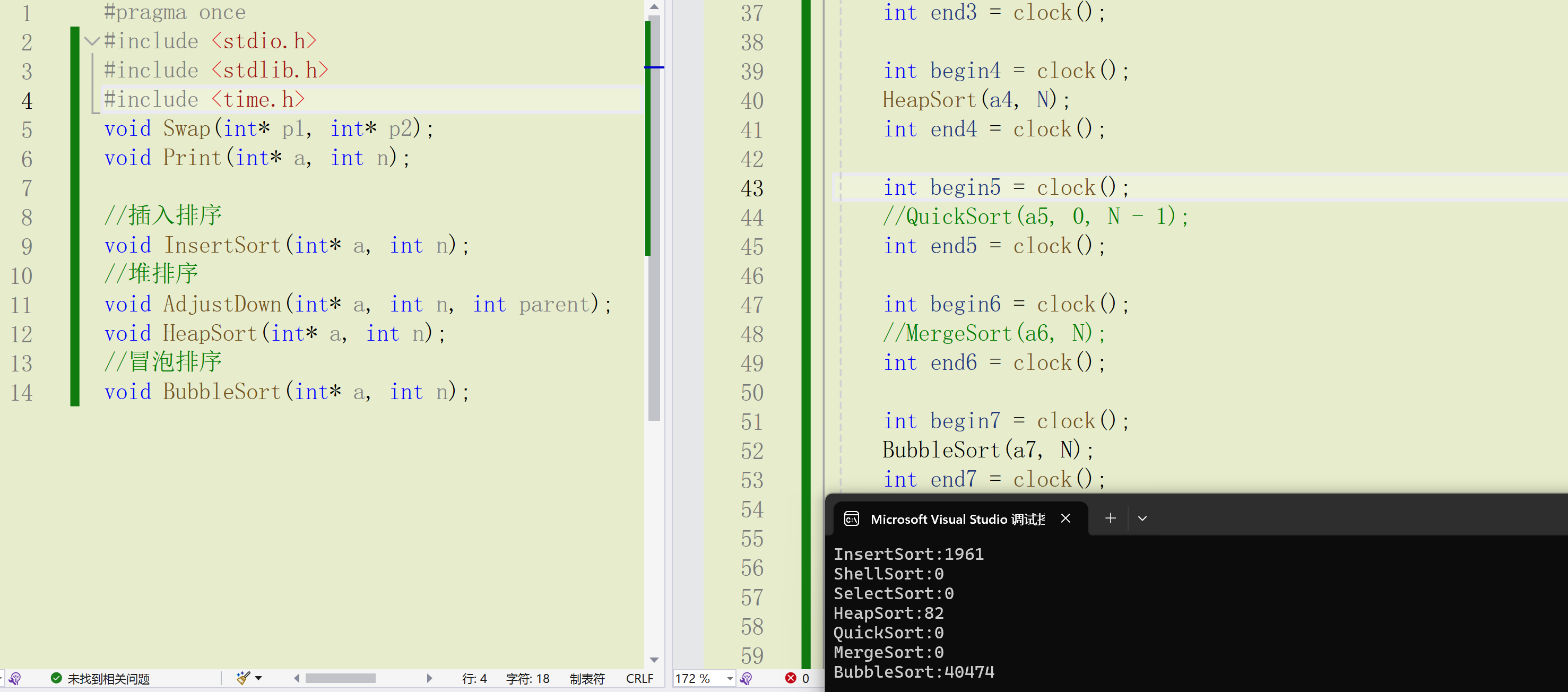
我们进行对比这三个排序发现:
相比于堆排序,插入排序和堆排序还是相对来说比较慢的,冒泡排序耗时就比较长了
3. 希尔排序
3.1 基本思想和排序的实现
插入排序在逆序的时候效率就下来了,那如何能解决这个问题呢:
- 预排序(让数组接近有序)
- 插入排序
预排序就是将数组分成多组,然后将组内优先排完
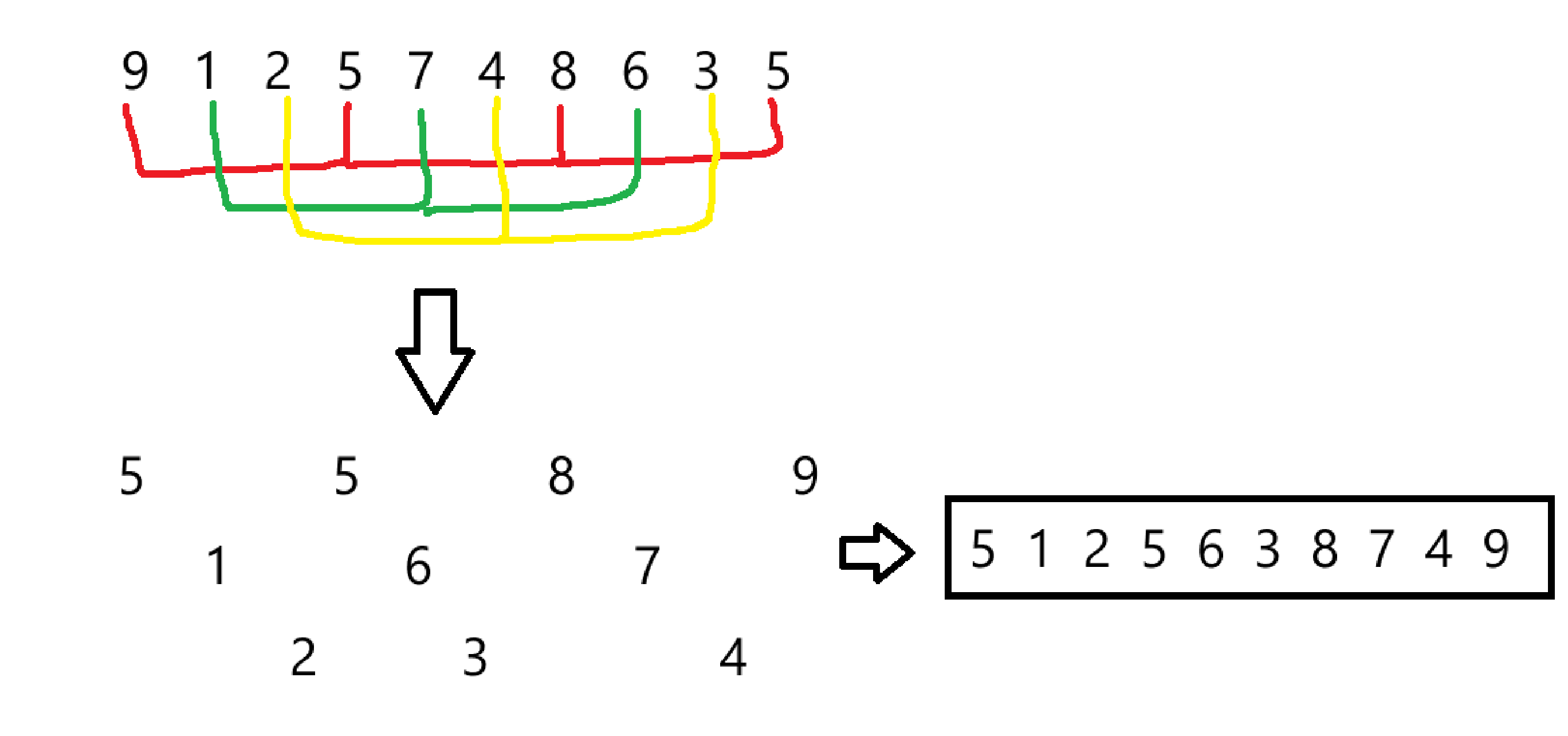
我们先将红色的组实现:
- 先写交换逻辑
cpp
int gap = 3;//间隔3个数为一组
int end = 0;
int tmp = a[end + gap];//这一组下一个数据的位置
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;- 再将红色的逻辑补全
cpp
int gap = 3;//间隔3个数为一组
for (int i = 0; i < n; i += gap)
{
int end = i;
int tmp = a[end + gap];//这一组下一个数据的位置
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}但是这里会存在越界,当i在n到n-2的位置时,对tmp进行赋值的时候会+3,导致数组访问越界
改成n - gap就行了
cpp
int gap = 3;//间隔3个数为一组
for (int i = 0; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];//这一组下一个数据的位置
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}其实这里也能发现:如果gap为1的时候就是我们之前写的插入排序
那么怎么排三组呢?
其实再套个循环就可以解决了:
cpp
for (int i = 0; i < gap; i++)
{
for (int i = 0; i < n - gap; i += gap)
{
int end = i;
int tmp = a[end + gap];//这一组下一个数据的位置
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}当然也可以多组并着走,进而减少一个循环(但是效率上并没有任何区别):
cpp
int gap = 3;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}3.2 gap的值
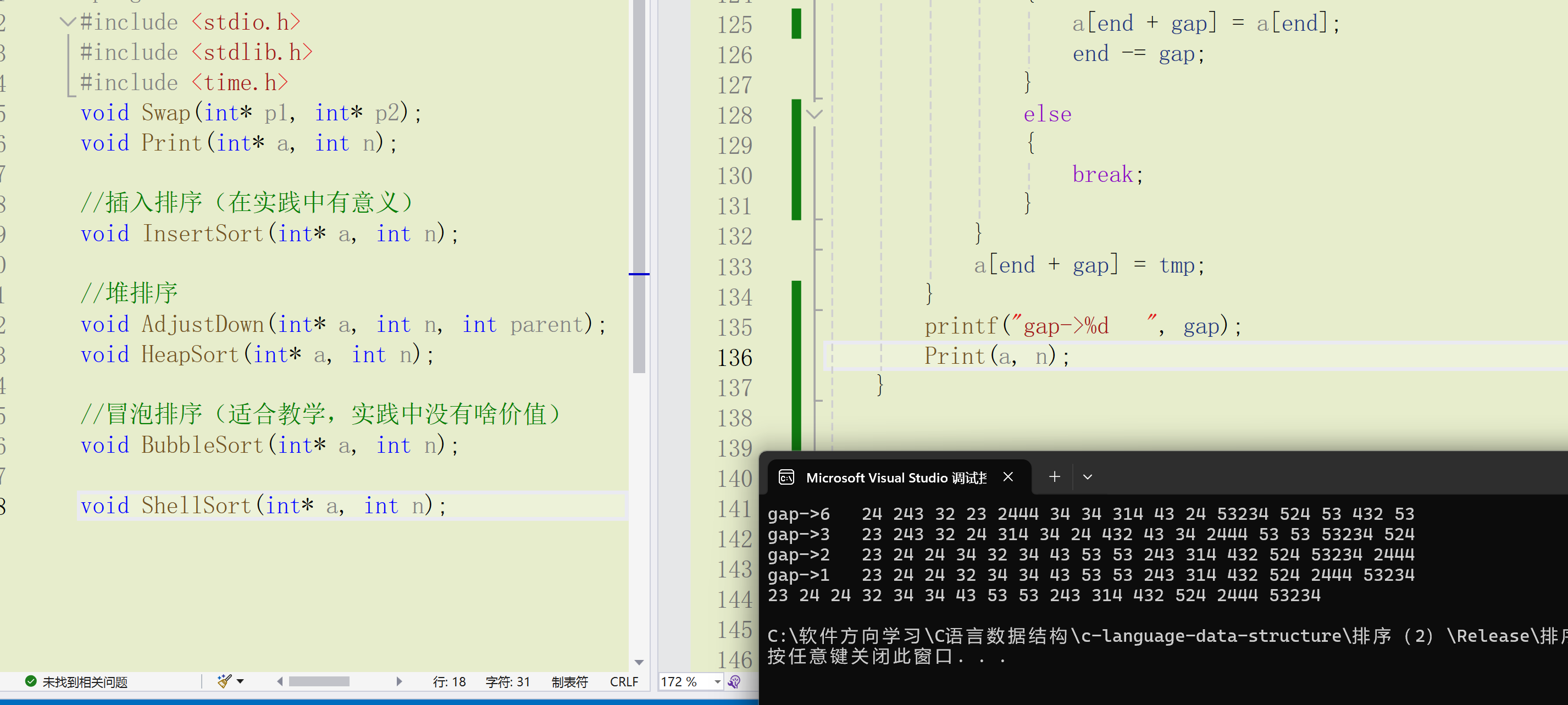
- gap的值越大,可以越快跳到后面,小的数可以越快调到前面,越不接近有序
- gap的值越小,跳的越慢,越接近有序,当gap==1时相当于排序就有序了
那gap究竟该给多少呢?
一般来说让gap走多组预排序:
cpp
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}gap = gap / 3 + 1
这样保证最后一次时gap的值直接就是1,就直接有序了
3.3 优缺点分析
我们先进行速度的比较,可以发现
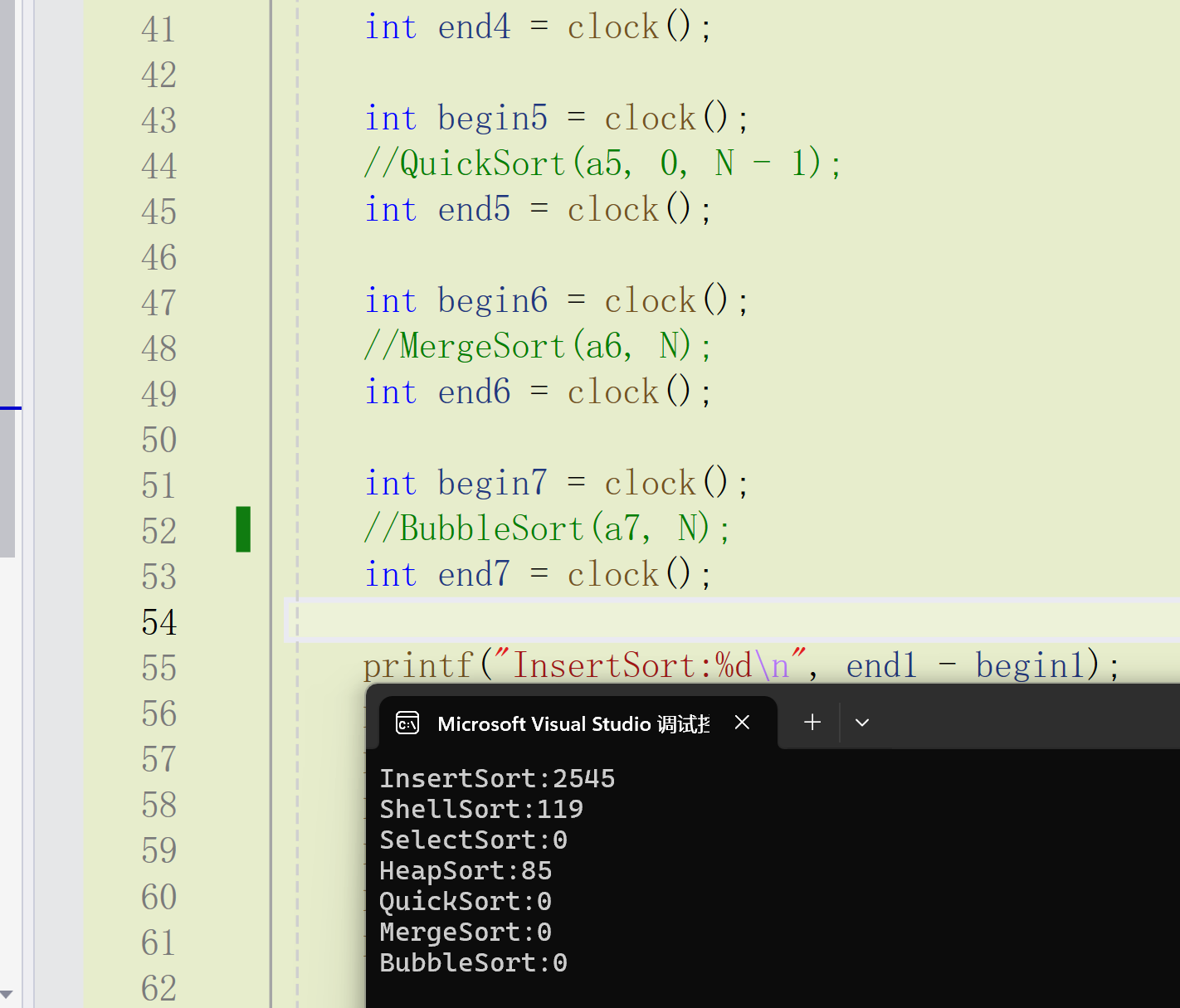
希尔排序的时间复杂度接近于 O(N^1.3)
这个时间复杂度比较难计算,感兴趣的可以看一下下面这篇文章: