计算机23级数据结构上机实验（第3-4周）

Romanticroom2024-11-15 17:04

A 二叉树删除子树

编写程序对给定二叉树执行若干次删除子树操作，输出每次删除子树后剩余二叉树的中根序列。二叉树结点的数据域值为不等于0的整数。每次删除操作是在上一次删除操作后剩下的二叉树上执行。

输入格式:

输入第1行为一组用空格间隔的整数，表示带空指针信息的二叉树先根序列，其中空指针信息用0表示。例如1 5 8 0 0 0 6 0 0表示如下图的二叉树。第2行为整数m，表示要进行的删除操作次数。接下来m行，每行一个不等于0的整数K，表示要删除以K为根的子树。m不超过100，二叉树结点个数不超过5000。输入数据保证各结点数据值互不相等，且删除子树后二叉树不为空。

输出格式:

输出为m行，每行为一组整数，表示执行删除操作后剩余二叉树的中根序列（中根序列中每个整数后一个空格）。若要删除的子树不在当前二叉树中，则该行输出0（0后无空格）。

输入样例:

1 5 8 0 0 0 6 0 0
3
5
8
6

输出样例:

1 6 
0
1
cpp 复制代码 
#include<iostream>
#include<cstring>
#include<string>
#include<unordered_map>
using namespace std;
const int N = 1e4;
int m;
int idx, cnt;
bool st[N];
unordered_map<int, int>ma;
struct tree {
	int v;
	int r, l;
	int father;
}p[N];

int build(int root) {
    int x;
    cin>>x;
	if (x == 0) {
		return 0;
	}
	p[root].v = x;
    ma[x]=root;
	p[root].l = build(++idx);
	p[root].r = build(++idx);
	return root;
}
void print(int root)
{
	if (st[root]) {
		return;
	}
	if (root == 0) {
		return;
	}
	print(p[root].l);
	cout << p[root].v << " ";
	print(p[root].r);
}
void Delete(int root) {
	if (root == 0) {
		return;
	}
	ma[p[root].v] = 0;
	Delete(p[root].l);
	Delete(p[root].r);
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	build(++idx);
	cin >> m;
	while (m--) {
		int k;
		cin >> k;
		if (!ma[k]) {
			cout << 0 << endl;
		}
		else {
			st[ma[k]] = true;
			print(1);
			cout << endl;
			Delete(ma[k]);
		}
	}
}

B 重建二叉树

给定非空二叉树的中根序列和后根序列，请编写程序创建该二叉树，计算其高度和先根序列；如给定的中根和后根序列不合法，则亦能识别。

输入格式:

输入包含多组数据（不超过10组），每组为两行字符串，第一行表示某二叉树的后根序列，第二行表示其中根序列。结点的值均为A-Z的大写字母，故二叉树结点个数不超过26，且保证输入的两个序列都是结点的全排列，但不一定是合法的中根和后根序列。输入保证不是空二叉树。

输出格式:

对于每组数据，如果输入的序列不合法（不是同一棵树的中根序列和后根序列），则输出INVALID；若输入序列合法，输出为两行，第一行为一个整数，表示该二叉树的高度，第二行为一个字符串，表示该二叉树的先根序列。

输入样例1:

CEFDBHGA
CBEDFAGH
CBEDFAGH
CEFDBHGA
BCA 
CAB

输出样例1:

3
ABCDEFGH
INVALID
INVALID

经典先序，后序加中序遍历建树板子，如果有需要可以看看我有关二叉树建树的分享。

这个题外加一个判断是否为一个二叉树。

cpp 复制代码 
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
const int N = 100;
struct tree {
	char c;
	int l, r;
}p[N];
char s1[N];
char s2[N];
int cnt;
int max_h;
int m;
bool flag = 1;
int build(int al, int ar, int bl, int br,int h) {
	if (al > ar) {
		return 0;
	}
	int root = ar;
	char cc = s1[ar];
	int k = 0;
	while (s1[ar] != s2[k]) {
		k++;
	}
	int len = k - bl;
	p[root].c = cc;
	cnt++;
	if (max_h < h) {
		max_h = h;
	}
	if (bl + len - 1 < 0) {
		return 0;
	}
	if (cnt >m ) {
		flag = 0;
		return 0;
	}
	p[root].l = build(al, al + len - 1, bl, bl + len - 1,h+1);
	p[root].r = build(al + len, ar - 1, bl + len + 1, br,h+1);
	return root;
}
void print(int root) {
	cout << p[root].c;
	if (p[root].l > 0) {
		print(p[root].l);
	}
	if (p[root].r > 0) {
		print(p[root].r);
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	while (cin >> s1+1 && cin >> s2+1) {
		flag = 1;
		m = strlen(s1+1);
		cnt = 0;
		max_h = 0;
		build(1,m,1,m,0);
		if (cnt < m||!flag) {
			cout << "INVALID" << endl;
		}
		else {
			cout << max_h << endl;
			print(m);
			cout << endl;
		}
	}
}

C 最右子表达式

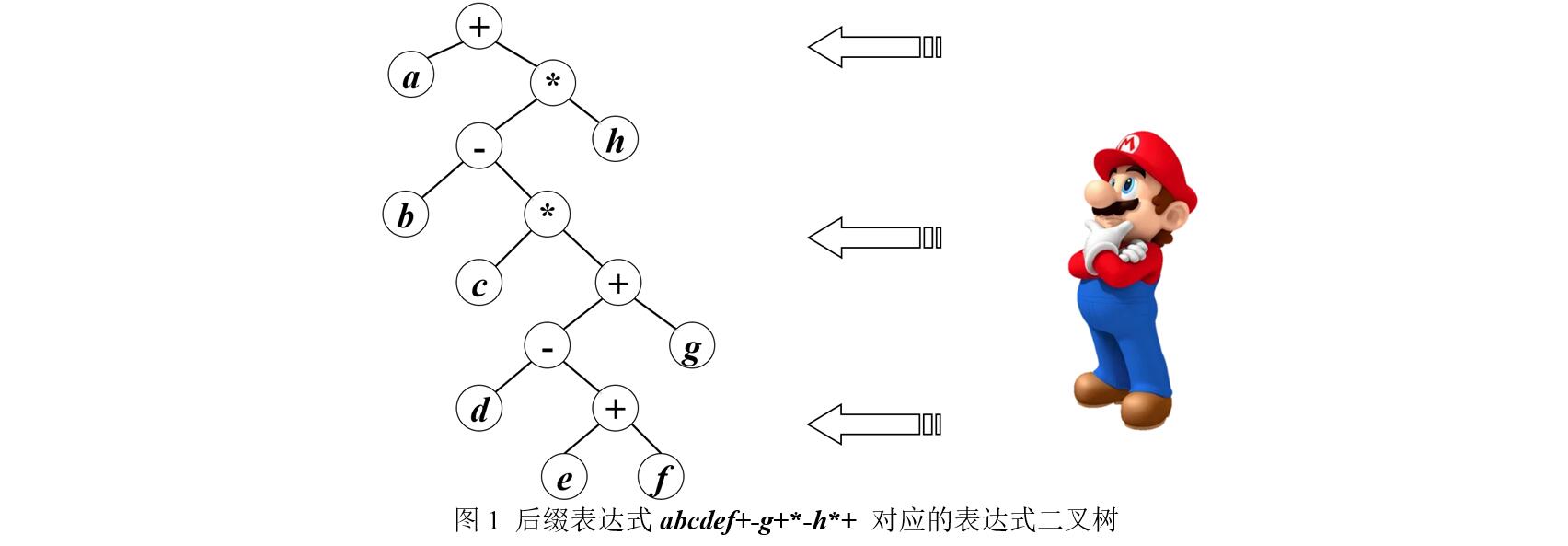
表达式可以对应一个树结构，称为表达式树。其中的叶结点对应表达式中的操作数，非叶结点对应运算符，假定所有运算均为二元运算。根据后缀表达式可以构造出表达式二叉树，方法是：从左向右扫描后缀表达式，每扫描到一个符号就生成一个二叉树结点，该符号作为结点的数据域值；若扫描到的符号是操作数，则将此操作数结点压栈；若扫描到的符号是运算符，则从栈中弹出两个结点，分别作为当前运算符结点的右、左孩子，再将当前运算符结点压栈。表达式扫描完成后，栈顶即为表达式树的根结点。表达式树的后根序列即为后缀表达式。

现给定一个后缀表达式exp，请编写程序求出exp的"最右子表达式"。exp的"最右子表达式"是指从exp对应的表达式树右边看向树，从第0层到最底层所能看到的各结点。例如后缀表达式abcdef+−g+∗−h∗+对应的表达式树如图1所示，其最右子表达式为 +∗h∗+g+f 。

输入格式:

第一行是正整数n ，表示后缀表达式的数目，1<n ≤100。接下来n 行，每行是一个由字母构成的字符串，长度不超过500，表示一个后缀表达式，其中小写字母表示操作数，大写字母表示运算符。所有运算符均为二元运算符。

输出格式:

对每个后缀表达式，输出其"最右子表达式"。

输入样例1:

6
abcdefXYgXZYhZX
xyPzwIM
abcABdefgCDEF
abcMN
bcMaN
fgCeDdEbcAaBF

输出样例1:

XZhZXgXf
MIw
FEDCg
NMc
Nac
FBacg

输入样例2:

6
vesBdtIBU
crpNWgaQmGG
jhAhRnlCJzU
laaKuqBHfzVEJ
rngAlKCpwgFIM
kcqoDYoDeqiYFDL

输出样例1:

UBIt
GGma
UzClh
JEVzq
MIFgg
LDFYio

这道题主要是按照题目所描述的方式建树，即非递归引入栈建立二叉树。

cpp 复制代码 
#include<iostream>
#include<cstring>
#include<string>
#include<stack>
using namespace std;
const int N = 1010;
int n, m;
bool st[N];
struct tree {
	char c;
	int l, r;
	int h;
}p[N];
int idx;
char s[N];
int root;
void build() {
	stack<char> q;
	stack<int> in;
	for (int i = 1; i <= n; i++) {
		char c = s[i];
		if (c >= 'a' && c <= 'z') {
			q.push(c);
			p[++idx].c = c;
			in.push(idx);
		}
		else {
			char x = q.top();
			q.pop();
			char y = q.top();
			q.pop();
			int a = in.top();
			in.pop();
			int b = in.top();
			in.pop();
			p[++idx].c = c;
			p[idx].r = a;
			p[idx].l = b;
			q.push(c);
			in.push(idx);
		}
	}
	root = in.top();
}
void fh(int r,int hh) {
	p[r].h = hh;
	if (p[r].l) {
		fh(p[r].l, hh + 1);
	}
	if (p[r].l) {
		fh(p[r].r, hh + 1);
	}
	
}
void print(int r) {
	if (!st[p[r].h]) {
		cout << p[r].c;
		st[p[r].h] = true;
	}
	if (p[r].r) {
		print(p[r].r);
	}
	if (p[r].l) {
		print(p[r].l);
	}

}
void init()
{
	for (int i = 1; i < N; i++) {
		p[i].c = 0;
		p[i].l = 0;
		p[i].r = 0;
		p[i].h = 0;
	}
	root = 0;
	idx = 0;
	memset(st, false, sizeof(st));
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> m;
	while (m--) {
		cin >> s + 1;
		init();
		n = strlen(s + 1);
		build();
		fh(root, 0);
		print(root);
		cout << endl;
	}
}

D 哈夫曼树

编写一个哈夫曼编码译码程序。针对一段文本，根据文本中字符出现频率构造哈夫曼树，给出每个字符的哈夫曼编码，并进行译码，计算编码前后文本大小。

为确保构建的哈夫曼树唯一，本题做如下限定：

  1. 选择根结点权值最小的两棵二叉树时，选取权值较小者作为左子树。
  2. 若多棵二叉树根结点权值相等，则先生成的作为左子树，后生成的作为右子树，具体来说：i) 对于单结点二叉树，优先选择根结点对应字母在文本中最先出现者，如文本为cba，三个字母均出现1次，但c在文本中最先出现，b第二出现，故则选择c作为左子树，b作为右子树。ii) 对于非单结点二叉树，先生成的二叉树作为左子树，后生成的二叉树作为右子树。iii. 若单结点和非单结点二叉树根结点权值相等，优先选择单结点二叉树。
  3. 生成哈夫曼编码时，哈夫曼树左分支标记为0，右分支标记为1。

输入格式:

输入为3行。第1行为一个字符串，包含不超过5000个字符，至少包含两个不同的字符，每个字符为a-z的小写字母。第2、3行为两个由0、1组成的字符串，表示待译码的哈夫曼编码。

输出格式:

输出第一行为用空格间隔的2个整数，分别为压缩前后文本大小，以字节为单位，一个字符占1字节，8个二进制位占1字节，若压缩后文本不足8位，则按1字节算。输出从第二行开始，每行为1个字符的哈夫曼编码，按各字符在文本中出现次数递增顺序输出，若多个字符出现次数相同，则按其在文本出现先后排列。每行格式为"字母:编码"。最后两行为两行字符串，表示译码结果，若译码失败，则输出INVALID。

输入样例:

cbaxyyzz
0100
011

输出样例:

8 3
c:100
b:101
a:110
x:111
y:00
z:01
zy
INVALID

这是本次作业的难题了，但是它本身没有难度，主要是熟练哈夫曼建树的模板（有兴趣的可以看看我关于哈夫曼树建树的分享），再加上对一些优先级的限定，我这里采用的是优先队列，目的是省去比较函数，但是如果不熟练的话自己写一个结构体的比较函数就好了。

cpp 复制代码 
#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
const int N = 5010;
typedef pair<int, int>PII;
typedef pair<int, char>PLL;
string str;
string s1, s2;
int nu[200];
int idx, cnt;
bool st[200];
unordered_map<char, string>ma;
priority_queue<PII, vector<PII>, greater<PII>>q;
priority_queue < pair<int, PLL>, vector < pair<int, PLL>>, greater<pair<int, PLL>>>qq;
struct tree {
	char c;
	int num;
	int l, r;
}p[N];
void get_map(int root,string s)
{
	if (p[root].c) {
		ma[p[root].c] = s;
		return;
	}
	get_map(p[root].l, s + '0');
	get_map(p[root].r, s + '1');
}
void get_ma(string s) {
	int r = idx;
	string ans1 = "";
	int root = idx;
	for (int i = 0;i < s.size();i++) {
		if (s[i] == '0') {
			root = p[root].l;
		}
		else {
			root = p[root].r;
		}
		if (p[root].c) {
			ans1 += p[root].c;
			if (i == s.size() - 1) {
				cout << ans1 << endl;
			}
			root = idx;
		}
		else {
			if (i == s.size() - 1) {
				cout << "INVALID" << endl;
			}
		}
		
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> str >> s1 >> s2;
	int n1 = str.size();
	for (int i = 0;i < str.size();i++) {
		char c = str[i];
		if (!nu[c]) {
			p[++idx].c = c;
			cnt++;
		}
		nu[c]++;
	}
	for (int i = 1;i <= idx;i++) {
		char cc = p[i].c;
		qq.push({ nu[cc],{i,cc} });
	}
	for (int i = 1;i < 200;i++) {
		if (nu[i]) {
			for (int j = 1;j <= idx;j++) {
				if (p[j].c == (char)i) {
					p[j].num = nu[i];
					//cout << p[j].c << " " << p[j].num << endl;
					q.push({ nu[i],j });
				}
			}
		}
	}
	while (q.size() > 1) {
		auto x = q.top();
		q.pop();
		auto y = q.top();
		q.pop();
		p[++idx].num = p[x.second].num + p[y.second].num;
		p[idx].l = x.second;
		p[idx].r = y.second;
		q.push({ p[idx].num,idx });
		//cout << p[idx].num << endl;
	}
	get_map(idx, "");
	int n2 = 0;
	for (int i = 0;i < str.size();i++) {
		int x = ma[str[i]].size();
		n2 += x;
	}
	if (n2 % 8) {
		n2 = n2 / 8 + 1;
	}
	else {
		n2 = n2 / 8;
	}
	cout << n1 << " "<<n2 << endl;
	//cout << cnt << endl;
	while (qq.size()) {
		auto t = qq.top();
		qq.pop();
		char cc = t.second.second;
		cout << cc << ":" << ma[cc] << endl;
	}
	get_ma(s1);
	get_ma(s2);

}

E 罪犯帮派

Tabu市的警察局决定结束混乱，因此要采取行动根除城市中的几大帮派。目前的问题是，给出两个罪犯，他们是属于同一帮派么？城市里一共有多少个帮派？假设在Tabu市现有n名罪犯，编号为1到n，给出m条消息表示属于同一帮派的两个罪犯编号。请基于这些不完全的信息帮助警方计算出他们想要的信息。

输入格式:

输入第一行为三个正整数，n、m和q。n为罪犯数；m为给出的已知信息数量；q为查询数。接下来m行，每行2个正整数a和b，表示罪犯a和罪犯b属于同一帮派。接下来q行，每行2个正整数c和d，即查询罪犯c和d是否属于同一帮派。每行输入的整数以空格间隔，n、m、q均不超过1000。

输出格式:

输出为q+1行，前q行对应于输入的q个查询的结果，如果属于同一帮派，则输出"In the same gang."，否则输出"In different gangs."。最后一行为一个整数，表示帮派数目。

输入样例:

3 2 1
1 2
2 3
1 3

输出样例:

In the same gang.
1

并查集没什么好说的。。

cpp 复制代码 
#include<iostream>
using namespace std;
const int N = 1010;
int p[N];
int n, m, q;
int cnt;
int find(int x) {
	if (p[x] != x) {
		p[x] = find(p[x]);
	}
	return p[x];
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	cin >> n >> m >> q;
	for (int i = 1; i <= n; i++) {
		p[i] = i;
	}
	cnt = n;
	for (int i = 1; i <= m; i++) {
		int a, b;
		cin >> a >> b;
		int x = find(a);
		int y = find(b);
		if (x != y) {
			p[x] = y;
			cnt--;
		}
	}
	for (int i = 1; i <= n; i++) {
		p[i] = find(p[i]);
	}
	for (int i = 1; i <= q; i++) {
		int a, b;
		cin >> a >> b;
		if (p[a] == p[b]) {
			cout << "In the same gang." << endl;
		}
		else {
			cout << "In different gangs." << endl;
		}
	}
	cout << cnt;
}

F 二叉树路径和II

编写程序找出非空二叉树中和最大的路径，二叉树结点为不等于0的整数。本题的"路径"定义为二叉树中的结点序列vi​,...,vj​，序列中前一个结点是后一个结点的父结点，但路径不一定是以根结点为起点，也不一定是以叶结点为终点。路径的和定义为该路径所包含的所有结点的数据值之和。

输入格式:

输入为一组用空格间隔的整数，个数不超过100个，表示带空指针信息的二叉树先根序列。

输出格式:

输出为两行，第一行为该二叉树路径和的最大值，第二行为一组整数，每个整数后一个空格，表示该最大路径包含的结点值（按所在层数递增顺序输出）。如果存在多条满足条件的路径，则输出最短（包含结点个数最少）者，如果存在多条最短的路径，则输出最靠左上者。

输入样例1:

1 2 0 0 3 0 0

输出样例1:

4
1 3

输入样例2:

-1 2 0 0 3 4 0 0 0

输出样例2:

7
3 4

输入样例3:

3 2 0 0 -1 4 0 0 0

输出样例3:

6
3 -1 4

这道题还是有点恶心到我了。。

cpp 复制代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int idx;
int max_num=-0x3f3f3f3f;
int min_cn=0x3f3f3f3f;
int ans[N];
bool flag;
struct tree {
	int v;
	int l, r;
	int num;
}p[N];
int build(int root) {
	int val;
	cin >> val;
	if (val == 0) {
		return 0;
	}
	p[root].v = val;
	p[root].l = build(++idx);
	p[root].r = build(++idx);
	return root;
}
void get_maxnum(int root,int num){
    if(root==0){
        return ;
    }
    p[root].num=num+p[root].v;
    if(p[root].num>max_num){
        max_num=p[root].num;
    }
    if(p[root].num<=0){
        get_maxnum(p[root].l,0);
        get_maxnum(p[root].r,0);
    }else{
        get_maxnum(p[root].l,p[root].num);
        get_maxnum(p[root].r,p[root].num);
    }
}
void get_mincn(int root,int h1,int h2){
    if(root==0){
        return;
    }
    if(p[root].num==max_num){
        min_cn=min(min_cn,h2-h1);
    }
    if(p[root].num<=0){
        h1=h2+1;
    }
    get_mincn(p[root].l,h1,h2+1);
    get_mincn(p[root].r,h1,h2+1);
    
}
void print(int root,int h1,int h2){
    if(root==0){
        return;
    }
    ans[h2]=p[root].v;
    if(p[root].num==max_num&&h2-h1==min_cn){
        for(int i=h1;i<=h2;i++){
            cout<<ans[i]<<" ";
        }
        return ;
    }
    if(p[root].num<=0){
        h1=h2+1;
    }
    print(p[root].l,h1,h2+1);
    print(p[root].r,h1,h2+1);
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
	build(++idx);
	get_maxnum(1,0);
    get_mincn(1,0,0);
	cout<<max_num<<endl;
    print(1,0,0);
	

}
相关推荐
TaoYuan__1 小时前
机器学习的常用算法
人工智能·算法·机器学习
用户40547878374822 小时前
深度学习笔记 - 使用YOLOv5中的c3模块进行天气识别
算法
shinelord明2 小时前
【再谈设计模式】建造者模式~对象构建的指挥家
开发语言·数据结构·设计模式
十七算法实验室2 小时前
Matlab实现麻雀优化算法优化随机森林算法模型 （SSA-RF）（附源码）
算法·决策树·随机森林·机器学习·支持向量机·matlab·启发式算法
黑不拉几的小白兔2 小时前
PTA部分题目C++重练
开发语言·c++·算法
迷迭所归处2 小时前
动态规划 —— dp 问题-买卖股票的最佳时机IV
算法·动态规划
chordful3 小时前
Leetcode热题100-32 最长有效括号
c++·算法·leetcode·动态规划
_OLi_3 小时前
力扣 LeetCode 459. 重复的子字符串（Day4：字符串）
算法·leetcode·职场和发展·kmp
白藏y3 小时前
数据结构——归并排序
数据结构·算法·排序算法
热门推荐
01玄机平台应急响应—webshell查杀02Ubuntu 20.04使用Livox mid 360 测试 FAST_LIO03【HarmonyOS】HUAWEI DevEco Studio 下载地址汇总04新版微信小程序获取用户手机号05文件或文件夹名称中有空格如何批量去除06组基轨迹建模 GBTM的介绍与实现（Stata 或 R）07【TC3xx芯片】TC3xx芯片电源管理系统PMS详解08优化手机性能，解决卡顿问题：关闭这3个微信开关，释放内存空间09基于YOLOv10深度学习的CT扫描图像肾结石智能检测系统【python源码+Pyqt5界面+数据集+训练代码】深度学习实战、目标检测10智能车联网安全发展形势、挑战