下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
提示:
1 <= nums1.length <= nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 104
nums1和nums2中所有整数 互不相同
nums1 中的所有整数同样出现在 nums2 中
进阶:你可以设计一个时间复杂度为 O(nums1.length + nums2.length) 的解决方案吗?
题解
根据题意,我们需要找到数组 nums2 中的每元素的 最先的 下一个 更大的元素,没有则为-1
根据 最先的 下一个 更大的元素,我们采用单调栈进行解题
首先我们分析一下如何找到最先的下一个更大的元素
我们可以对于每一个 nums2 元素都进行遍历,寻找其后面的比他大的元素
但是这样的时间复杂度太高了
遍历完数组 nums2 需要 O(n^2)
所以我们采用单调栈对算法进行优化
我们可以这么理解 如何找到找到最先的下一个更大的元素
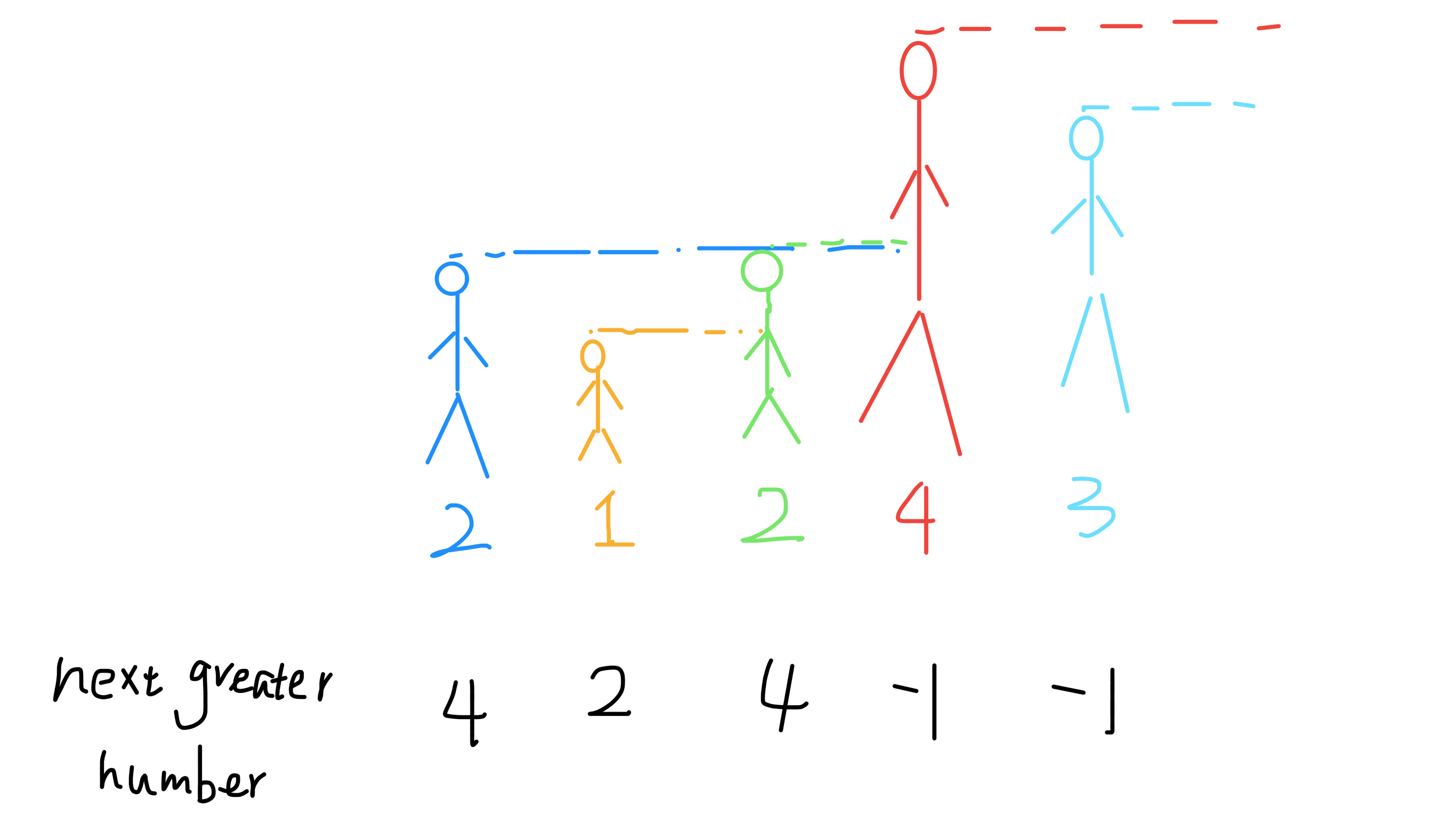
图片来源
作者:labuladong
来源:力扣(LeetCode)
例如:此时我们需要寻找 nums[ i ] 的下一个更大的元素
如果之后有元素 小于 nums[ i ] ,那么它就被 nums[ i ] 给挡住了,在 nums[ i ] 之前的所有元素都不可能看见它了
也就是说
当寻找 nums[ i ] 的下一个更大的元素时,我们只需要记得 nums[ i ] 和比 nums[ i ] 更大的元素
比 nums[ i ] 小的都被挡住了,所以就不需要考虑了
那么我就可以使用单调栈对这一信息进行存储
对于遍历到的 nums[ i ]
首先将栈中所有比它小的元素都出栈
如果此时栈不为空则栈顶的元素就是 nums[ i ] 的下一个更大的元素
else 说明没有更的,依据要求为 -1
然后将 nums[ i ] 进栈即可
关于上述操作的时间复杂度
虽然使用了两层循环,但是我们可以发现
内层循环 即出栈操作
当整个循环结束后,最多也就执行 n 次
所以整个循环的时间复杂度是 O(n)
接下来要考虑的问题就是如何存储 nums[ i ] 的下一个更大的元素这些数据
由于题目是根据值来进行查找的
我们便使用哈希表将值对应的下一个更大的元素进行存储
最后遍历数组 nums1
根据值取访问哈希表得到数据即可
代码如下↓
c
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
*returnSize = nums1Size;
int arr[10001];
int* res = (int*)malloc(sizeof(int)*nums1Size);
int stack[nums2Size];
int f = -1;
for(int i=nums2Size-1;i>-1;i--)
{
while(f!=-1 && nums2[i]>stack[f])
{
f--;
}
if(f==-1)
{
arr[nums2[i]]=-1;
}
else
{
arr[nums2[i]]=stack[f];
}
stack[++f]=nums2[i];
}
for(int i=0;i<nums1Size;i++)
{
res[i]=arr[nums1[i]];
}
return res;
}