《数字图像处理》实验3-频率域处理方法

一、实验核心概述

1. 实验目标

理解图像频域处理的本质，掌握空间域与频域的转换逻辑；
熟练运用 MATLAB 实现二维傅里叶变换、逆变换及频谱可视化；
验证二维 DFT 的分解特性，理解不同图像的频谱分布差异；
掌握理想低通滤波器（ILPF）的设计与频域去噪应用。

2. 实验环境

操作系统：Windows 8/10/11
软件版本：MATLAB 2014 及以上版本

3. 核心原理与关键函数

频域基础：图像低频对应平缓区域（如背景），高频对应边缘、噪声等变化剧烈区域；
核心变换：fft2（二维傅里叶变换）、ifft2（二维傅里叶逆变换）；
辅助操作：fftshift（频谱中心化）、log(1+abs(F))（频谱可视化，压缩动态范围）；
滤波逻辑：频域滤波 = 傅里叶变换 → 滤波器与频域图像相乘 → 逆傅里叶变换。

二、完整实验内容与代码实现

（一）傅里叶变换与频谱可视化

实验任务

读取彩色图像→转换为灰度图→傅里叶变换→频谱中心化→可视化原图、灰度图及频谱图。

完整代码

复制代码

% 读取彩色图像
img_rgb = imread('阿狸.jpg'); 

% 将彩色图像转换为灰度图
img_gray = rgb2gray(img_rgb); 

% 对灰度图进行二维傅里叶变换（需转换为double类型）
F = fft2(double(img_gray)); 

% 频谱中心化（将低频成分移到图像中心）
F_shift = fftshift(F); 

% 计算频谱的幅值，并取对数以便于显示（避免数值范围过大导致显示失真）
F_mag = log(1 + abs(F_shift)); 

% 创建figure窗口，展示结果
figure('Name','傅里叶变换实验','NumberTitle','off');
subplot(1,3,1); imshow(img_rgb); title('原图');
subplot(1,3,2); imshow(img_gray); title('灰度图');
subplot(1,3,3); imshow(F_mag, []); title('变换频谱'); % []自动映射灰度范围

实验结果

频谱图中心为亮斑（低频成分集中），四周亮度逐渐降低（高频成分）；
图像中边缘、细节越多，频谱四周的高频成分越明显。

（二）傅里叶变换与逆变换验证

实验任务

实现 "灰度图→傅里叶变换→逆变换" 流程，对比原图与逆变换结果的一致性。

完整代码

复制代码

% 读取彩色图像
img_rgb = imread('天火三玄变.jpg'); 

% 转换为灰度图
img_gray = rgb2gray(img_rgb);

% 转为double类型以进行傅里叶变换
img_gray_double = double(img_gray);

% 二维傅里叶变换
F = fft2(img_gray_double);

% 频谱中心化（用于可视化）
F_shift = fftshift(F);
F_mag = log(1 + abs(F_shift));

% 傅里叶逆变换（还原回空间域）
img_recon = ifft2(F);

% 逆变换结果可能包含极小虚部，取实部并转换回uint8类型
img_recon = uint8(real(img_recon));

% 比较原图与逆变换图像矩阵是否相同
isSame = isequal(img_gray, img_recon);
if isSame
    fprintf('原图与逆变换图像矩阵是否完全相同: 是\n');
else
    fprintf('原图与逆变换图像矩阵是否完全相同: 否（微小差异由浮点运算精度导致）\n');
end

% 可视化结果
figure('Name', 'FFT 与逆变换实验', 'NumberTitle', 'off');
subplot(1,4,1); imshow(img_rgb); title('原图');
subplot(1,4,2); imshow(img_gray); title('灰度图');
subplot(1,4,3); imshow(F_mag, []); title('二维傅里叶变换');
subplot(1,4,4); imshow(img_recon); title('傅里叶逆变换');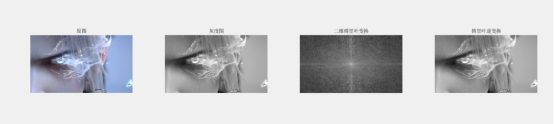

实验结果

逆变换图像与原图视觉完全一致，矩阵对比存在微小误差（浮点运算导致）；
验证了傅里叶变换的可逆性，为 "频域处理→空间域还原" 提供技术支撑。

（三）不同图像的频谱对比

实验任务

读取两张不同图像，转换为灰度图后分别进行傅里叶变换，对比频谱分布差异。

完整代码

复制代码

% 读取两张彩色图像
img1_rgb = imread('ALi.jpg'); 
img2_rgb = imread('天火三玄变.jpg'); 

% 转换为灰度图
img1_gray = rgb2gray(img1_rgb);
img2_gray = rgb2gray(img2_rgb);

% 转换为double类型以进行傅里叶变换
img1_double = double(img1_gray);
img2_double = double(img2_gray);

% 二维傅里叶变换
F1 = fft2(img1_double);
F2 = fft2(img2_double);

% 频谱中心化
F1_shift = fftshift(F1);
F2_shift = fftshift(F2);

% 计算幅值谱，并取对数以便显示
F1_mag = log(1 + abs(F1_shift));
F2_mag = log(1 + abs(F2_shift));

% 可视化对比结果
figure('Name', '傅里叶频谱对比', 'NumberTitle', 'off');
subplot(2,2,1); imshow(img1_gray); title('原图灰度图1');
subplot(2,2,2); imshow(img2_gray); title('原图灰度图2');
subplot(2,2,3); imshow(F1_mag, []); title('频谱图1');
subplot(2,2,4); imshow(F2_mag, []); title('频谱图2');

实验结果

频谱差异：平缓区域多的图像（如简单卡通图）频谱低频集中，高频微弱；细节丰富的图像（如复杂场景图）频谱高频成分更分散、亮度更高；
频谱对称性：傅里叶变换频谱满足共轭对称性，表现为以中心为原点的对称分布。

（四）二维 DFT 的分解验证

实验任务

验证 "二维 DFT = 行一维 DFT + 列一维 DFT"，对比直接fft2与分步骤fft的结果。

完整代码

复制代码

% 读取彩色图像并转换为灰度图
img_rgb = imread('阿狸2.jpg'); 
img_gray = rgb2gray(img_rgb);
img_double = double(img_gray);

%% 方法1：直接使用fft2进行二维傅里叶变换
F_fft2 = fft2(img_double);
F_fft2_shift = fftshift(F_fft2);
F_fft2_mag = log(1 + abs(F_fft2_shift));

%% 方法2：使用fft分两步实现（先对行，再对列）
F_row = fft(img_double, [], 2);  % 对每一行做一维傅里叶变换
F_2step = fft(F_row, [], 1);     % 对结果的每一列做一维傅里叶变换
F_2step_shift = fftshift(F_2step);
F_2step_mag = log(1 + abs(F_2step_shift));

%% 可视化两种方法的结果
figure('Name', '二维DFT分解验证', 'NumberTitle', 'off');
subplot(1,3,1); imshow(img_gray); title('原图');
subplot(1,3,2); imshow(F_fft2_mag, []); title('fft2实现变换');
subplot(1,3,3); imshow(F_2step_mag, []); title('fft实现变换');

%% 验证两种方法结果的一致性（允许微小浮点误差）
diff_matrix = abs(F_fft2 - F_2step);
max_error = max(diff_matrix(:));
fprintf('两种方法结果的最大误差: %.2e\n', max_error);
if max_error < 1e-8
    fprintf('验证结论：两种方法在理论上一致，微小误差由浮点运算精度导致。\n');
else
    fprintf('验证结论：结果差异超出预期，需检查代码。\n');
end

实验结果

两种方法的频谱图视觉完全一致，最大误差小于 1e-8；
验证了二维 DFT 的可分解性，为算法优化（如并行计算）提供理论依据。

（五）高斯噪声抑制：理想低通滤波

实验任务

为图像添加高斯噪声，设计理想低通滤波器，在频域实现去噪并可视化结果。

完整代码

复制代码

% 配置参数：学号末位数M=7，截止频率D0=M*10=70
student_id_last_digit = 7;
D0 = student_id_last_digit * 10;  % 理想低通滤波器截止频率

% 读取彩色图像并转换为灰度图
img_raw = imread('AALi.jpg'); 
img_gray = rgb2gray(img_raw);

% 为灰度图添加高斯白噪声
img_noise = imnoise(img_gray, 'gaussian');

% 对加噪图像做傅里叶变换并中心化（用于可视化和滤波）
fft_img_noise = fft2(double(img_noise));
fftshift_img_noise = fftshift(fft_img_noise);

% 获取图像尺寸，构造理想低通滤波器
[rows, cols] = size(img_noise);
H = zeros(rows, cols);  % 初始化滤波器掩模
center_row = rows / 2;  % 频域中心行坐标
center_col = cols / 2;  % 频域中心列坐标

% 遍历每个频率点，计算到中心的距离并生成滤波器
for i = 1:rows
    for j = 1:cols
        % 计算频率点(i,j)到中心的欧氏距离
        distance = sqrt((i - center_row)^2 + (j - center_col)^2);
        % 理想低通滤波器：距离≤D0则保留（H=1），否则抑制（H=0）
        if distance <= D0
            H(i, j) = 1;
        else
            H(i, j) = 0;
        end
    end
end

% 频域滤波：滤波器掩模与频域图像逐元素相乘
filtered_fftshift = fftshift_img_noise .* H;

% 逆傅里叶变换，还原回空间域
filtered_img = ifft2(ifftshift(filtered_fftshift));
filtered_img = real(filtered_img);  % 去除微小虚部

% 计算滤波后图像的频谱（用于可视化）
filtered_fft = fftshift(fft2(filtered_img));

% 可视化所有结果
figure('Name', '高斯加噪与理想低通滤波', 'NumberTitle', 'off');
subplot(2, 2, 1); imshow(img_noise); title('加噪后图像');
subplot(2, 2, 2); imshow(log(abs(fftshift_img_noise) + 1), []); title('噪声fft');
subplot(2, 2, 3); imshow(filtered_img, []); title('滤波后噪声图');
subplot(2, 2, 4); imshow(log(abs(filtered_fft) + 1), []); title('滤波后噪声图fft');

实验结果

加噪图像：因高斯噪声（高频成分）出现颗粒感；
滤波后图像：高频噪声被抑制，图像平滑，但边缘细节有轻微模糊（理想低通滤波器的振铃效应）；
频谱变化：滤波后频谱高频区域亮度显著降低，仅保留中心低频成分。

三、实验总结与关键知识点

1. 核心技术梳理

实验模块	核心函数	核心结论
频谱可视化	`fft2`、`fftshift`、`log(1+abs(F))`	低频对应平缓区域，高频对应边缘 / 噪声
变换可逆性	`ifft2`	逆变换可还原原图，支持频域处理流程
DFT 分解	`fft`（分两步）	二维 DFT 可通过两次一维 DFT 实现
低通滤波	自定义 ILPF 掩模	抑制高频噪声，代价是边缘模糊

2. 关键注意事项

数据类型：fft2需输入double类型，避免uint8运算溢出；
频谱显示：必须通过log(1+abs(F))压缩动态范围，否则频谱过暗无法观察；
逆变换处理：需用real()去除虚部，再转换为uint8以正常显示；
滤波器设计：滤波器尺寸需与频域图像一致，频率点距离计算基于频域中心。

3. 应用场景拓展

频域去噪：低通滤波器（理想、高斯、巴特沃斯）适用于抑制高频噪声；
图像增强：高通滤波器增强边缘细节，适用于模糊图像锐化；
图像压缩：利用频域能量集中在低频的特点，舍弃高频成分实现高效压缩（如 JPEG）。

通过本次实验，系统掌握了频率域图像处理的核心流程与关键技术，理解了傅里叶变换的本质与应用价值，为后续复杂频域滤波器设计与优化奠定了坚实基础。