问题描述
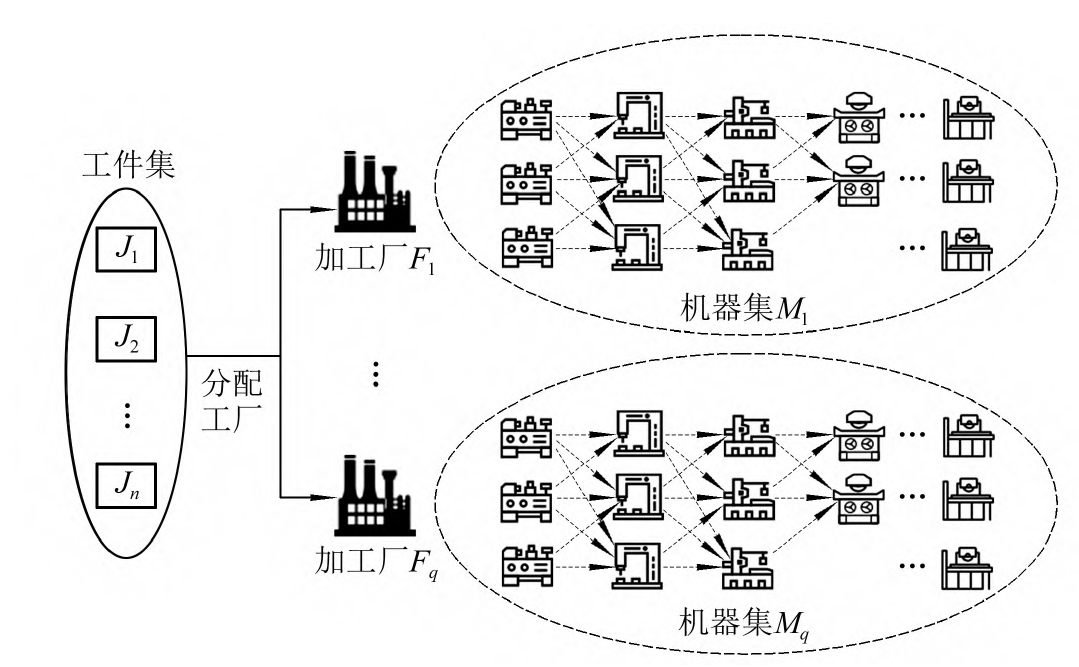
分布式柔性作业车间调度(Distributed FJSP,DFJSP)主要包含工序序列 、机器的选择 和工厂的选择三个子问题。首先将𝑛个工件分配到不同的工厂当中,然后在每个工厂为工件选择可加工的机器以及确定工件的加工顺序。该问题的主要目标是通过调整工件在哪个工厂加工、工件序列的排序以及工件选择哪台机器加工,从而实现最小化最大完工时间的目标。
模型构建
DFJSP 可描述如下:给定的 n n n个加工工件,在 N f N_f Nf个工厂中加工,每个工厂有 m f m_f mf台机床。每个工件 i i i可选择在任一工厂加工。并且,每个工件 i i i包含
n i n_i ni道工序,工序 O i , j O_{i,j} Oi,j可选在工厂 f f f中的 m i , j , f m_{i,j,f} mi,j,f个加工机床上加工。
DFJSP 的假设条件如下:
(1)所有工件、机器以及工厂在零时刻都可用;
(2)每个机器在同一时刻只能处理一个工序;
(3)工件在加工处理过程中不能被中断;
(4)工件的所有工序都按照预先设定好的顺序,不允许提前或者推后;
(5)一个工件只能在一个工厂中处理,同时一个工序只能在一台机器处理;
(6)不考虑机器故障和准备时间;
具体的参数、变量以及数学模型可见上一篇推文:
优化问题|文化基因算法求解分布式柔性作业车间调度问题及MATLAB代码实现
算法思路
编码规则
编码包括三部分工序顺序(operation sequence,OS), 车间分配(factory assignment,FA), 和机器选择(machine select, MS)
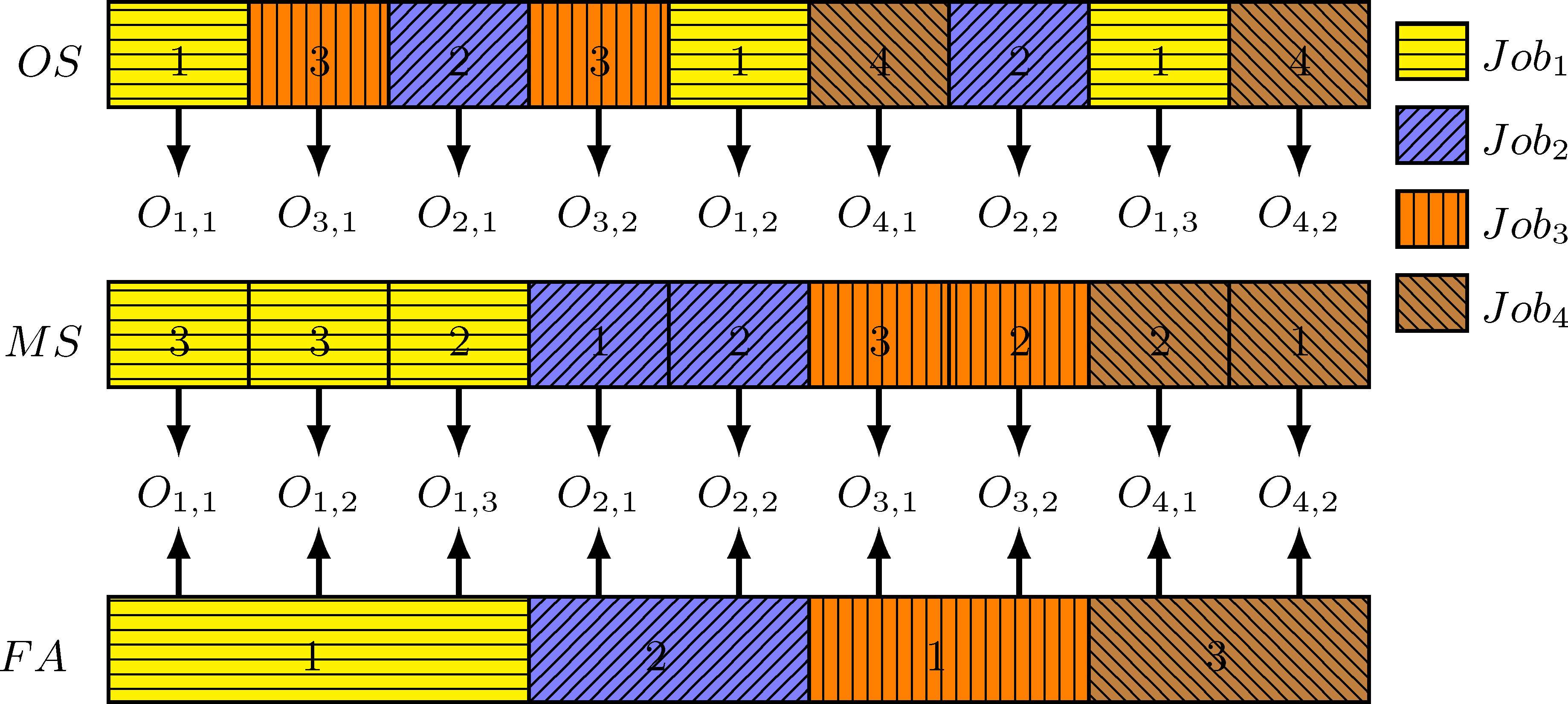
初始解生成
- 为每个工件随机选择可生产的车间
- 随机产生工序加工顺序
- 为每道工序随机选择可加工的机器
基于Deep-Q-Network(DQN)的邻域选择模型
在算法运行不同阶段,采用合理的局部搜索算子可以有效的提高算法性能。然而,现有局部搜索算法主要是采用随机选择或按照某一顺序选择局部搜索算子。DQN是一种基于当前状态、自主选择最优动作的强化学习方法。因此,将传统算法中随机选择局部搜索算子过程,转化为由DQN推荐当前状态下的最优局部搜索算子。它的基本要素包括:状态空间、动作空间与奖励。

算法框架伪代码如下:

部分代码
N6邻域算子
def N6(p_chrom, m_chrom, f_chrom, fitness, num_job, job_operation_matrix, num_operation, time, num_machine, num_factory):
s1 = p_chrom
s2 = np.zeros(num_operation, dtype=int)
p = np.zeros(num_job, dtype=int)
for i in range(num_operation):
p[s1[i]] = p[s1[i]] + 1
s2[i] = p[s1[i]]
P0 = []
P = []
IP = []
FJ = []
for f in range(num_factory):
P.append([])
IP.append([])
FJ.append([])
for i in range(num_operation):
t1 = s1[i]
t2 = s2[i]
t3 = f_chrom[t1]
P[t3].append(p_chrom[i])
IP[t3].append(i)
for i in range(num_job):
t3 = f_chrom[i]
FJ[t3].append(i)
cf = int(fitness[2])
CP, CB, block = FindCriticalPathDHFJSP(P[cf], m_chrom, FJ[cf], cf, num_job, job_operation_matrix, time, num_machine)
for i in range(block):
BL=len(CB[i])
if BL>1:
if i==0:
Index1=int(np.floor(random.random()*(BL-1)))
Index2=BL-1
Index1=CB[i][Index1];Index2=CB[i][Index2]
tmp=P[cf][Index1]
for j in range(Index1,Index2):
P[cf][j]=P[cf][j+1]
P[cf][Index2]=tmp
if i==block-1:
Index1=0
Index2=int(np.floor(random.random()*(BL-1))+1)
Index1 = CB[i][Index1];Index2 = CB[i][Index2]
tmp = P[cf][Index2]
for j in range(Index2, Index1,-1):
P[cf][j] = P[cf][j-1]
P[cf][Index1] = tmp
if i>0 and i<block-1 and BL>2:
Index1 = int(np.floor(random.random() * (BL - 2)) + 1)
Index2=BL-1
Index1 = CB[i][Index1];Index2 = CB[i][Index2]
tmp = P[cf][Index1]
for j in range(Index1, Index2):
P[cf][j] = P[cf][j + 1]
P[cf][Index2] = tmp
Index1 = 0
Index2 = int(np.floor(random.random() * (BL - 2)) + 1)
Index1 = CB[i][Index1];Index2 = CB[i][Index2]
tmp = P[cf][Index2]
for j in range(Index2, Index1, -1):
P[cf][j] = P[cf][j - 1]
P[cf][Index1] = tmp
newm=m_chrom
newf=f_chrom
newp=np.zeros(num_operation,dtype=int)
for f in range(num_factory):
L=len(IP[f])
for i in range(L):
newp[IP[f][i]]=P[f][i]
return newp,newm,newfDQN网络
class DQN(object):
def __init__(self, inDim, outDim, BATCH_SIZE, LR, EPSILON, GAMMA, MEMORY_CAPACITY, TARGET_REPLACE_ITER):
self.eval_net, self.target_net = Net(inDim, outDim), Net(inDim, outDim)
self.N_STATES = inDim
self.N_ACTIONS = outDim
self.learn_step_counter = 0 # for target updating
self.memory_counter = 0 # for storing memory
self.BATCH_SIZE = BATCH_SIZE
self.LR = LR
self.EPSILON = EPSILON
self.GAMMA = GAMMA
self.MEMORY_CAPACITY = MEMORY_CAPACITY
self.TARGET_REPLACE_ITER = TARGET_REPLACE_ITER
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
# self.optimizer = torch.optim.SGD(self.eval_net.parameters(), lr=LR)
# memory是一个np数组,每一行代表一个记录,状态 动作 奖励 新的状态
self.memory = np.zeros((MEMORY_CAPACITY, self.N_STATES * 2 + 2)) # initialize memory
self.loss_func = nn.MSELoss()
self.eval_net, self.target_net = self.eval_net.cuda(), self.target_net.cuda()
self.loss_func = self.loss_func.cuda()
def choose_action(self, x):
x = torch.unsqueeze(torch.FloatTensor(x), 0).cuda()
# input only one sample
if np.random.uniform() < self.EPSILON: # greedy
actions_value = self.eval_net.forward(x) # shape=(1, action)
actions_value = actions_value.cuda()
actions_value = actions_value.cpu()
actions_value = actions_value.detach().numpy()
actions_value[actions_value <= 0] = 0.001 # 不能有负概率
actions_value = actions_value / np.sum(actions_value) # 归一化
action = max(actions_value)
actions_value_ = actions_value[0]
index = 0
max_v = actions_value_[0]
for i in range(1,self.N_ACTIONS):
if max_v < actions_value_[i]:
index = i
max_v = actions_value_[i]
max_action = np.array([index])
for i in range(self.N_ACTIONS):
if max_v == actions_value_[i] and index != i:
max_action = np.hstack((max_action, i))
ml = len(max_action)
if ml > 1:
bction = random.randint(0, ml-1)
action = max_action[bction]
else:
action = max_action[0]
else: # random
action = np.random.randint(0, self.N_ACTIONS)
return action
def learn(self):
# target parameter update
if self.learn_step_counter % self.TARGET_REPLACE_ITER == 0:
self.target_net.load_state_dict(self.eval_net.state_dict())
self.learn_step_counter += 1
# sample batch transitions
sample_index = np.random.choice(self.MEMORY_CAPACITY, self.BATCH_SIZE)
b_memory = self.memory[sample_index, :]
b_current_state = torch.FloatTensor(b_memory[:, :self.N_STATES])
b_action = torch.LongTensor(b_memory[:, self.N_STATES:self.N_STATES + 1].astype(int))
b_reward = torch.FloatTensor(b_memory[:, self.N_STATES + 1 : self.N_STATES + 2])
b_next_state = torch.FloatTensor(b_memory[:, - self.N_STATES:])
b_current_state = b_current_state.cuda() # current state
b_action = b_action.cuda() # current action
b_reward = b_reward.cuda() # current reward
b_next_state = b_next_state.cuda() # next state
# q_eval w.r.t the action in experience
q_eval = self.eval_net(b_current_state).gather(1, b_action) # shape (batch, 1)
q_next = self.target_net(b_next_state).detach() # detach from graph, don't backpropagate
q_target = b_reward + self.GAMMA * q_next.max(1)[0].view(self.BATCH_SIZE, 1) # shape (batch, 1)
loss = self.loss_func(q_eval, q_target)
losses = loss.cpu()
losses = losses.detach().numpy()
print('train loss MSE =', losses)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
return losses参考文献
R. Li, W. Gong, L. Wang, C. Lu and C. Dong, "Co-Evolution With Deep Reinforcement Learning for Energy-Aware Distributed Heterogeneous Flexible Job Shop Scheduling," in IEEE Transactions on Systems, Man, and Cybernetics: Systems, doi: 10.1109/TSMC.2023.3305541.
若有运筹优化建模及算法定制需求,欢迎联系我们私聊沟通
