回归(Regression)
- 引言
- [1. 线性激活(Linear Activation)](#1. 线性激活(Linear Activation))
- [2. 均方误差损失(Mean Squared Error Loss)](#2. 均方误差损失(Mean Squared Error Loss))
- [3. 均方误差损失导数(Mean Squared Error Loss Derivative)](#3. 均方误差损失导数(Mean Squared Error Loss Derivative))
- [4. 平均平方误差 (MSE) 损失代码(Mean Squared Error (MSE) Loss Code)](#4. 平均平方误差 (MSE) 损失代码(Mean Squared Error (MSE) Loss Code))
- [5. 平均绝对误差损失(Mean Absolute Error Loss)](#5. 平均绝对误差损失(Mean Absolute Error Loss))
- [6. 平均绝对误差损失导数(Mean Absolute Error Loss Derivative)](#6. 平均绝对误差损失导数(Mean Absolute Error Loss Derivative))
- [7. 平均绝对误差损失代码(Mean Absolute Error Loss Code)](#7. 平均绝对误差损失代码(Mean Absolute Error Loss Code))
- [8. 回归精度(Accuracy in Regression)](#8. 回归精度(Accuracy in Regression))
- [9. 回归模型训练(Regression Model Training)](#9. 回归模型训练(Regression Model Training))
- 到此为止的全部代码:
引言
到目前为止,我们一直在处理分类模型,目标是确定某个事物是什么。现在我们感兴趣的是基于输入来确定一个具体的数值。例如,你可能希望使用神经网络来预测明天的温度或一辆车的价格。对于这样的任务,我们需要输出更加精细的结果。这也意味着我们需要一种新的方法来衡量损失,并且需要一个新的输出层激活函数!同时,这也意味着我们所用的数据不同。我们需要包含目标标量数值的训练数据,而不是分类数据。
python
import matplotlib.pyplot as plt
import nnfs
from nnfs.datasets import sine_data
nnfs.init()
X, y = sine_data()
plt.plot(X, y)
plt.show()上面的数据将生成类似的图表:
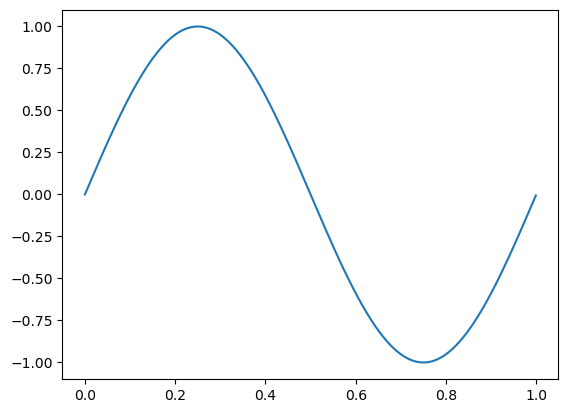
1. 线性激活(Linear Activation)
由于我们不再使用分类标签,而是要预测一个标量数值,因此我们将对输出层使用线性激活函数 。该线性函数不会修改输入,而是将其直接传递到输出: y = x y = x y=x。在反向传播过程中,我们已经知道 f ( x ) = x f(x) = x f(x)=x的导数是1;因此,我们新线性激活函数的完整类定义为:
python
# Linear activation
class Activation_Linear:
# Forward pass
def forward(self, inputs):
# Just remember values
self.inputs = inputs
self.output = inputs
# Backward pass
def backward(self, dvalues):
# derivative is 1, 1 * dvalues = dvalues - the chain rule
self.dinputs = dvalues.copy()这可能会引发一个问题:为什么我们甚至要编写一些什么都不做的代码?在前向传播中,我们只是将输入传递到输出,在反向传播中同样处理梯度,因为为了应用链式法则,我们将传入的梯度乘以导数,而导数为1。我们这样做只是为了完整性和清晰性,以便在模型定义代码中看到输出层的激活函数。从计算时间的角度来看,这几乎不会增加任何处理时间,至少不会显著影响训练时间。
现在我们只需要解决损失函数的问题!
2. 均方误差损失(Mean Squared Error Loss)
由于我们不再使用分类标签,因此无法计算交叉熵 。相反,我们需要一些新的方法。回归任务中计算误差的两种主要方法是均方误差 (MSE)和平均绝对误差(MAE)。
对于均方误差,我们将预测值和真实值之间的差异取平方(对于多个回归输出,每个输出都会计算差异),然后对这些平方值求平均。
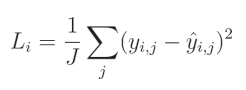
其中, y y y 表示目标值, y ^ \hat{y} y^ 表示预测值,索引 i i i 表示当前样本,索引 j j j 表示该样本中的当前输出, J J J 表示输出的数量。
这里的思想是,偏离目标值越远,惩罚越大。
3. 均方误差损失导数(Mean Squared Error Loss Derivative)
相对于预测值的平方误差偏导数为:
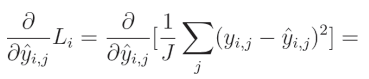
1 J \frac{1}{J} J1(输出数量 J J J 的倒数)是一个常数,可以移到导数的外部。由于我们是针对给定输出 j j j 计算导数,因此单个元素的求和结果等于该元素本身。
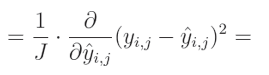
要计算一个表达式的幂的偏导数,我们需要将这个指数与该表达式相乘,然后从指数中减去1,并将其乘以内函数的偏导数:
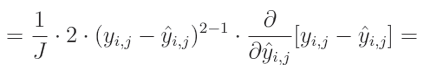
减法的偏导数等于偏导数的减法:
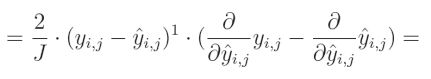
关于真实值对预测值的偏导数等于0,因为我们将其他变量视为常数。而预测值对自身的偏导数等于1,这导致结果为 0 − 1 = − 1 0-1=-1 0−1=−1。这个结果与方程的其余部分相乘,形成最终解:
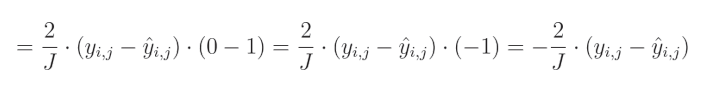
全面解决方案:
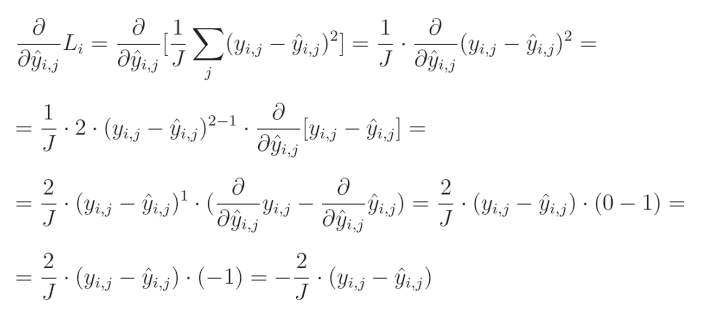
偏导数等于 − 2 -2 −2,再乘以真实值与预测值的差,然后除以输出的数量以对梯度进行归一化,从而使梯度的大小与输出的数量无关。
4. 平均平方误差 (MSE) 损失代码(Mean Squared Error (MSE) Loss Code)
MSE(均方误差)的代码实现包括了用于计算多个输出的样本损失的方程。axis=-1 与均值计算的含义在前一章节中已有详细解释,简而言之,它告诉NumPy对每个样本单独计算输出间的均值。在反向传播中,我们实现了导数方程,其结果为 − 2 -2 −2乘以真实值与预测值之间的差,并除以输出数量进行归一化。与其他损失函数实现类似,我们还对梯度按样本数量进行归一化,使其与批量大小或样本数量无关。
python
import numpy as np
# Mean Squared Error loss
class Loss_MeanSquaredError(Loss): # L2 loss
# Forward pass
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean((y_true - y_pred)**2, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Gradient on values
self.dinputs = -2 * (y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples5. 平均绝对误差损失(Mean Absolute Error Loss)
对于平均绝对误差 (Mean Absolute Error, MAE),你需要计算单个输出中预测值与真实值之间的绝对差值,然后对这些绝对值求平均:
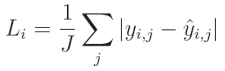
其中, y y y 表示目标值, y ^ \hat{y} y^ 表示预测值,索引 i i i 表示当前样本,索引 j j j 表示当前样本中的输出, J J J 表示输出的数量。
该函数作为损失函数时,对误差进行线性惩罚。它会产生更加稀疏的结果,并对异常值具有较强的鲁棒性,这既可能是优点,也可能是缺点。实际上,L1(MAE)损失的使用频率低于L2(MSE)损失。
6. 平均绝对误差损失导数(Mean Absolute Error Loss Derivative)
绝对误差相对于预测值的偏导数为:
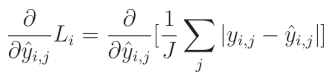
1 1 1 除以 J J J(输出数量)是一个常数,可以移到导数之外。由于我们是对给定输出 j j j 求导,所以一个元素的和等于该元素本身:
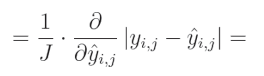
我们之前已经为L1正则化计算了绝对值的偏导数,这与L1损失类似。绝对值的导数在该值大于 0 0 0时等于 1 1 1,在该值小于 0 0 0时等于 − 1 -1 −1。当该值为 0 0 0时,导数不存在:
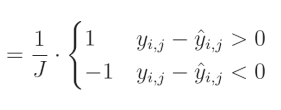
完整解决方案:
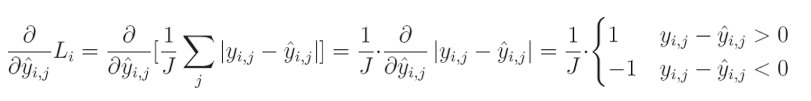
7. 平均绝对误差损失代码(Mean Absolute Error Loss Code)
均绝对误差(Mean Absolute Error, MAE)的代码与均方误差(Mean Squared Error, MSE)非常相似。前向传播中使用NumPy的np.abs()函数来计算绝对值,然后再计算均值。反向传播中,我们将使用np.sign()函数,该函数根据输入的符号返回 1 1 1或 − 1 -1 −1,如果参数等于 0 0 0,则返回 0 0 0。接着,我们将梯度根据样本数量进行归一化,使其不受批量大小或样本数量的影响:
python
import numpy as np
# Mean Absolute Error loss
class Loss_MeanAbsoluteError(Loss): # L1 loss
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean(np.abs(y_true - y_pred), axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Calculate gradient
self.dinputs = np.sign(y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples8. 回归精度(Accuracy in Regression)
既然我们已经有了数据、激活函数和用于回归的损失计算,我们接下来要衡量模型的性能。
在使用交叉熵时,我们可以计算预测与真实目标值相等的情况数,并将其除以样本数量,从而衡量模型的准确率。然而,对于回归模型,我们面临两个问题:
- 第一个问题是,模型中的每个输出神经元(可能有很多)都是单独的输出,这与分类器不同,分类器的所有输出会共同贡献于一个预测结果。
- 第二个问题是,回归模型的预测值是浮点数,我们无法简单地检查输出值是否与真实目标值完全相等,因为它很可能不会相等------即便只有微小的差异,准确率也会被计算为 0 0 0。例如,如果你的模型预测房价,其中某个样本的目标价格是 192 , 500 192,500 192,500,而预测值是 192 , 495 192,495 192,495,那么纯粹的"是否相等"评估会返回False。但考虑到数值的量级,这样的预测在实际中可以被视为"足够接近"或正确。
对于回归任务,没有完美的方法来衡量准确率。但为了直观展示性能,最好还是有一个准确率度量。例如,流行的深度学习框架Keras会同时展示回归模型的准确率和损失,我们也将定义自己的准确率指标。
首先,我们需要一个"限制"值,我们称之为"精度"(precision)。为了计算这个精度,我们将从真实目标值中计算标准差,并将其除以 250 250 250。根据你的目标,这个值可能会有所不同。分母越大,准确率指标就会越"严格"。这里我们选择 250 250 250作为分母。以下是表示这一过程的代码:
python
accuracy_precision = np.std(y) / 250然后,我们可以将这个精度值用作回归输出的"容差范围",在比较目标值和预测值的准确性时起到缓冲作用。我们通过对真实目标值与预测值之间的差异取绝对值来进行比较。接着,我们检查这个差异是否小于我们之前计算得到的精度值:
python
predictions = activation2.output
accuracy = np.mean(np.absolute(predictions - y) < accuracy_precision)9. 回归模型训练(Regression Model Training)
有了新的激活函数、损失和计算精度的方法,我们现在就可以创建模型了:
python
import numpy as np
import nnfs
from nnfs.datasets import spiral_data
from nnfs.datasets import sine_data
nnfs.init()
# Dense layer
class Layer_Dense:
# Layer initialization
def __init__(self, n_inputs, n_neurons,
weight_regularizer_l1=0, weight_regularizer_l2=0,
bias_regularizer_l1=0, bias_regularizer_l2=0):
# Initialize weights and biases
self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
self.biases = np.zeros((1, n_neurons))
# Set regularization strength
self.weight_regularizer_l1 = weight_regularizer_l1
self.weight_regularizer_l2 = weight_regularizer_l2
self.bias_regularizer_l1 = bias_regularizer_l1
self.bias_regularizer_l2 = bias_regularizer_l2
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs, weights and biases
self.output = np.dot(inputs, self.weights) + self.biases
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradients on regularization
# L1 on weights
if self.weight_regularizer_l1 > 0:
dL1 = np.ones_like(self.weights)
dL1[self.weights < 0] = -1
self.dweights += self.weight_regularizer_l1 * dL1
# L2 on weights
if self.weight_regularizer_l2 > 0:
self.dweights += 2 * self.weight_regularizer_l2 * self.weights
# L1 on biases
if self.bias_regularizer_l1 > 0:
dL1 = np.ones_like(self.biases)
dL1[self.biases < 0] = -1
self.dbiases += self.bias_regularizer_l1 * dL1
# L2 on biases
if self.bias_regularizer_l2 > 0:
self.dbiases += 2 * self.bias_regularizer_l2 * self.biases
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
# Dropout
class Layer_Dropout:
# Init
def __init__(self, rate):
# Store rate, we invert it as for example for dropout
# of 0.1 we need success rate of 0.9
self.rate = 1 - rate
# Forward pass
def forward(self, inputs):
# Save input values
self.inputs = inputs
# Generate and save scaled mask
self.binary_mask = np.random.binomial(1, self.rate, size=inputs.shape) / self.rate
# Apply mask to output values
self.output = inputs * self.binary_mask
# Backward pass
def backward(self, dvalues):
# Gradient on values
self.dinputs = dvalues * self.binary_mask
# ReLU activation
class Activation_ReLU:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs
self.output = np.maximum(0, inputs)
# Backward pass
def backward(self, dvalues):
# Since we need to modify original variable,
# let's make a copy of values first
self.dinputs = dvalues.copy()
# Zero gradient where input values were negative
self.dinputs[self.inputs <= 0] = 0
# Softmax activation
class Activation_Softmax:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Get unnormalized probabilities
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# Normalize them for each sample
probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
self.output = probabilities
# Backward pass
def backward(self, dvalues):
# Create uninitialized array
self.dinputs = np.empty_like(dvalues)
# Enumerate outputs and gradients
for index, (single_output, single_dvalues) in enumerate(zip(self.output, dvalues)):
# Flatten output array
single_output = single_output.reshape(-1, 1)
# Calculate Jacobian matrix of the output and
jacobian_matrix = np.diagflat(single_output) - np.dot(single_output, single_output.T)
# Calculate sample-wise gradient
# and add it to the array of sample gradients
self.dinputs[index] = np.dot(jacobian_matrix, single_dvalues)
# Sigmoid activation
class Activation_Sigmoid:
# Forward pass
def forward(self, inputs):
# Save input and calculate/save output
# of the sigmoid function
self.inputs = inputs
self.output = 1 / (1 + np.exp(-inputs))
# Backward pass
def backward(self, dvalues):
# Derivative - calculates from output of the sigmoid function
self.dinputs = dvalues * (1 - self.output) * self.output
# Linear activation
class Activation_Linear:
# Forward pass
def forward(self, inputs):
# Just remember values
self.inputs = inputs
self.output = inputs
# Backward pass
def backward(self, dvalues):
# derivative is 1, 1 * dvalues = dvalues - the chain rule
self.dinputs = dvalues.copy()
# SGD optimizer
class Optimizer_SGD:
# Initialize optimizer - set settings,
# learning rate of 1. is default for this optimizer
def __init__(self, learning_rate=1., decay=0., momentum=0.):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.momentum = momentum
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If we use momentum
if self.momentum:
# If layer does not contain momentum arrays, create them
# filled with zeros
if not hasattr(layer, 'weight_momentums'):
layer.weight_momentums = np.zeros_like(layer.weights)
# If there is no momentum array for weights
# The array doesn't exist for biases yet either.
layer.bias_momentums = np.zeros_like(layer.biases)
# Build weight updates with momentum - take previous
# updates multiplied by retain factor and update with
# current gradients
weight_updates = self.momentum * layer.weight_momentums - self.current_learning_rate * layer.dweights
layer.weight_momentums = weight_updates
# Build bias updates
bias_updates = self.momentum * layer.bias_momentums - self.current_learning_rate * layer.dbiases
layer.bias_momentums = bias_updates
# Vanilla SGD updates (as before momentum update)
else:
weight_updates = -self.current_learning_rate * layer.dweights
bias_updates = -self.current_learning_rate * layer.dbiases
# Update weights and biases using either
# vanilla or momentum updates
layer.weights += weight_updates
layer.biases += bias_updates
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adagrad optimizer
class Optimizer_Adagrad:
# Initialize optimizer - set settings
def __init__(self, learning_rate=1., decay=0., epsilon=1e-7):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache += layer.dweights**2
layer.bias_cache += layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# RMSprop optimizer
class Optimizer_RMSprop:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, rho=0.9):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.rho = rho
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache = self.rho * layer.weight_cache + (1 - self.rho) * layer.dweights**2
layer.bias_cache = self.rho * layer.bias_cache + (1 - self.rho) * layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adam optimizer
class Optimizer_Adam:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.beta_1 = beta_1
self.beta_2 = beta_2
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_momentums = np.zeros_like(layer.weights)
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# Update momentum with current gradients
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# Get corrected momentum
# self.iteration is 0 at first pass
# and we need to start with 1 here
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# Update cache with squared current gradients
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# Get corrected cache
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Common loss class
class Loss:
# Regularization loss calculation
def regularization_loss(self, layer):
# 0 by default
regularization_loss = 0
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Return loss
return data_loss
# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Number of samples in a batch
samples = len(y_pred)
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Probabilities for target values -
# only if categorical labels
if len(y_true.shape) == 1:
correct_confidences = y_pred_clipped[
range(samples),
y_true
]
# Mask values - only for one-hot encoded labels
elif len(y_true.shape) == 2:
correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)
# Losses
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of labels in every sample
# We'll use the first sample to count them
labels = len(dvalues[0])
# If labels are sparse, turn them into one-hot vector
if len(y_true.shape) == 1:
y_true = np.eye(labels)[y_true]
# Calculate gradient
self.dinputs = -y_true / dvalues
# Normalize gradient
self.dinputs = self.dinputs / samples
# Binary cross-entropy loss
class Loss_BinaryCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Calculate sample-wise loss
sample_losses = -(y_true * np.log(y_pred_clipped) + (1 - y_true) * np.log(1 - y_pred_clipped))
sample_losses = np.mean(sample_losses, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
clipped_dvalues = np.clip(dvalues, 1e-7, 1 - 1e-7)
# Calculate gradient
self.dinputs = -(y_true / clipped_dvalues - (1 - y_true) / (1 - clipped_dvalues)) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Squared Error loss
class Loss_MeanSquaredError(Loss): # L2 loss
# Forward pass
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean((y_true - y_pred)**2, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Gradient on values
self.dinputs = -2 * (y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Absolute Error loss
class Loss_MeanAbsoluteError(Loss): # L1 loss
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean(np.abs(y_true - y_pred), axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Calculate gradient
self.dinputs = np.sign(y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Softmax classifier - combined Softmax activation
# and cross-entropy loss for faster backward step
class Activation_Softmax_Loss_CategoricalCrossentropy():
# Creates activation and loss function objects
def __init__(self):
self.activation = Activation_Softmax()
self.loss = Loss_CategoricalCrossentropy()
# Forward pass
def forward(self, inputs, y_true):
# Output layer's activation function
self.activation.forward(inputs)
# Set the output
self.output = self.activation.output
# Calculate and return loss value
return self.loss.calculate(self.output, y_true)
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# If labels are one-hot encoded,
# turn them into discrete values
if len(y_true.shape) == 2:
y_true = np.argmax(y_true, axis=1)
# Copy so we can safely modify
self.dinputs = dvalues.copy()
# Calculate gradient
self.dinputs[range(samples), y_true] -= 1
# Normalize gradient
self.dinputs = self.dinputs / samples
# Create dataset
X, y = sine_data()
# Create Dense layer with 1 input feature and 64 output values
dense1 = Layer_Dense(1, 64)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 64 input features (as we take output
# of previous layer here) and 1 output value
dense2 = Layer_Dense(64, 1)
# Create Linear activation:
activation2 = Activation_Linear()
# Create loss function
loss_function = Loss_MeanSquaredError()
# Create optimizer
optimizer = Optimizer_Adam()
# Accuracy precision for accuracy calculation
# There are no really accuracy factor for regression problem,
# but we can simulate/approximate it. We'll calculate it by checking
# how many values have a difference to their ground truth equivalent
# less than given precision
# We'll calculate this precision as a fraction of standard deviation
# of al the ground truth values
accuracy_precision = np.std(y) / 250
# Train in loop
for epoch in range(10001):
# Perform a forward pass of our training data through this layer
dense1.forward(X)
# Perform a forward pass through activation function
# takes the output of first dense layer here
activation1.forward(dense1.output)
# Perform a forward pass through second Dense layer
# takes outputs of activation function
# of first layer as inputs
dense2.forward(activation1.output)
# Perform a forward pass through activation function
# takes the output of second dense layer here
activation2.forward(dense2.output)
# Calculate the data loss
data_loss = loss_function.calculate(activation2.output, y)
# Calculate regularization penalty
regularization_loss = loss_function.regularization_loss(dense1) + loss_function.regularization_loss(dense2)
# Calculate overall loss
loss = data_loss + regularization_loss
# Calculate accuracy from output of activation2 and targets
# To calculate it we're taking absolute difference between
# predictions and ground truth values and compare if differences
# are lower than given precision value
predictions = activation2.output
accuracy = np.mean(np.absolute(predictions - y) < accuracy_precision)
if not epoch % 100:
print(f'epoch: {epoch}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {optimizer.current_learning_rate}')
# Backward pass
loss_function.backward(activation2.output, y)
activation2.backward(loss_function.dinputs)
dense2.backward(activation2.dinputs)
activation1.backward(dense2.dinputs)
dense1.backward(activation1.dinputs)
# Update weights and biases
optimizer.pre_update_params()
optimizer.update_params(dense1)
optimizer.update_params(dense2)
optimizer.post_update_params()
python
>>>
epoch: 0, acc: 0.002, loss: 0.500 (data_loss: 0.500, reg_loss: 0.000), lr: 0.001
epoch: 100, acc: 0.003, loss: 0.346 (data_loss: 0.346, reg_loss: 0.000), lr: 0.001
...
epoch: 9900, acc: 0.003, loss: 0.145 (data_loss: 0.145, reg_loss: 0.000), lr: 0.001
epoch: 10000, acc: 0.004, loss: 0.145 (data_loss: 0.145, reg_loss: 0.000), lr: 0.001这里的训练效果并不理想!让我们添加绘制测试数据的功能,同时对测试数据进行前向传递,在同一张图上绘制输出数据:
python
import matplotlib.pyplot as plt
X_test, y_test = sine_data()
dense1.forward(X_test)
activation1.forward(dense1.output)
dense2.forward(activation1.output)
activation2.forward(dense2.output)
plt.plot(X_test, y_test)
plt.plot(X_test, activation2.output)
plt.show()首先,我们导入了matplotlib库,然后创建了一组新的数据。接下来,有4行代码与我们之前代码中前向传播的代码相同。我们可以将其称为预测,或者在我们接下来要讨论的内容中,将其视为验证。我们将在未来的章节中解释验证和预测是什么。目前,理解我们正在做的事情就足够了:我们在与训练模型相同的特征集上进行预测,以查看模型学习到了什么,并返回了什么结果------即输出与训练时的真实目标值有多接近。然后我们绘制训练数据(显然是一个正弦波)和预测数据(我们希望其也形成一个正弦波)。让我们再次运行这段代码,并查看生成的图像:
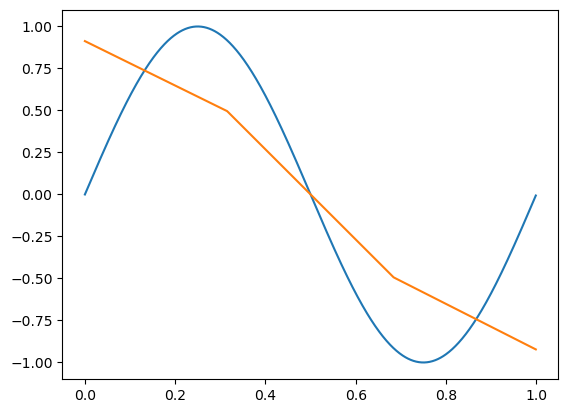
培训过程动画:
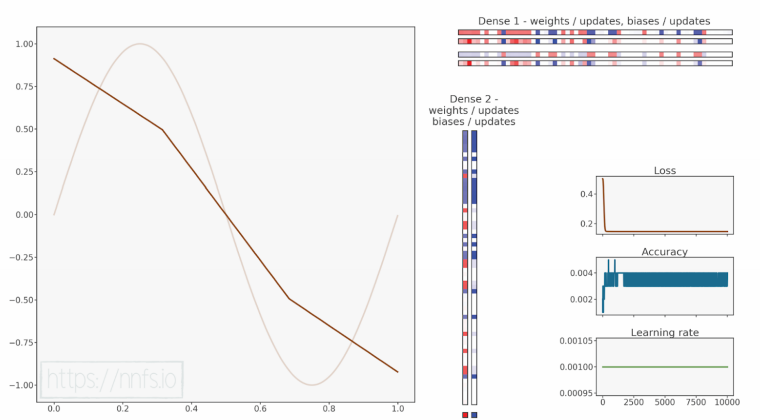
代码可视化:https://nnfs.io/ghi
回顾一下修正线性激活函数(ReLU),它的非线性行为使我们能够映射非线性函数,但我们还需要两个或更多隐藏层。而在这里,我们只有1个隐藏层,后面是输出层。正如我们现在应该知道的那样,这显然是不够的!
如果我们再增加一层:
python
# Create dataset
X, y = sine_data()
# Create Dense layer with 1 input feature and 64 output values
dense1 = Layer_Dense(1, 64)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 64 input features (as we take output
# of previous layer here) and 64 output values
dense2 = Layer_Dense(64, 64)
# Create ReLU activation (to be used with Dense layer):
activation2 = Activation_ReLU()
# Create third Dense layer with 64 input features (as we take output
# of previous layer here) and 1 output value
dense3 = Layer_Dense(64, 1)
# Create Linear activation:
activation3 = Activation_Linear()
# Create loss function
loss_function = Loss_MeanSquaredError()
# Create optimizer
optimizer = Optimizer_Adam()
# Accuracy precision for accuracy calculation
# There are no really accuracy factor for regression problem,
# but we can simulate/approximate it. We'll calculate it by checking
# how many values have a difference to their ground truth equivalent
# less than given precision
# We'll calculate this precision as a fraction of standard deviation
# of al the ground truth values
accuracy_precision = np.std(y) / 250
# Train in loop
for epoch in range(10001):
# Perform a forward pass of our training data through this layer
dense1.forward(X)
# Perform a forward pass through activation function
# takes the output of first dense layer here
activation1.forward(dense1.output)
# Perform a forward pass through second Dense layer
# takes outputs of activation function
# of first layer as inputs
dense2.forward(activation1.output)
# Perform a forward pass through activation function
# takes the output of second dense layer here
activation2.forward(dense2.output)
# Perform a forward pass through third Dense layer
# takes outputs of activation function of second layer as inputs
dense3.forward(activation2.output)
# Perform a forward pass through activation function
# takes the output of third dense layer here
activation3.forward(dense3.output)
# Calculate the data loss
data_loss = loss_function.calculate(activation3.output, y)
# Calculate regularization penalty
regularization_loss = loss_function.regularization_loss(dense1) + loss_function.regularization_loss(dense2) + loss_function.regularization_loss(dense3)
# Calculate overall loss
loss = data_loss + regularization_loss
# Calculate accuracy from output of activation2 and targets
# To calculate it we're taking absolute difference between
# predictions and ground truth values and compare if differences
# are lower than given precision value
predictions = activation3.output
accuracy = np.mean(np.absolute(predictions - y) < accuracy_precision)
if not epoch % 100:
print(f'epoch: {epoch}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {optimizer.current_learning_rate}')
# Backward pass
loss_function.backward(activation3.output, y)
activation3.backward(loss_function.dinputs)
dense3.backward(activation3.dinputs)
activation2.backward(dense3.dinputs)
dense2.backward(activation2.dinputs)
activation1.backward(dense2.dinputs)
dense1.backward(activation1.dinputs)
# Update weights and biases
optimizer.pre_update_params()
optimizer.update_params(dense1)
optimizer.update_params(dense2)
optimizer.update_params(dense3)
optimizer.post_update_params()
import matplotlib.pyplot as plt
X_test, y_test = sine_data()
dense1.forward(X_test)
activation1.forward(dense1.output)
dense2.forward(activation1.output)
activation2.forward(dense2.output)
dense3.forward(activation2.output)
activation3.forward(dense3.output)
plt.plot(X_test, y_test)
plt.plot(X_test, activation3.output)
plt.show()
python
>>>
epoch: 0, acc: 0.002, loss: 0.500 (data_loss: 0.500, reg_loss: 0.000), lr: 0.001
epoch: 100, acc: 0.003, loss: 0.187 (data_loss: 0.187, reg_loss: 0.000), lr: 0.001
...
epoch: 9900, acc: 0.617, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.001
epoch: 10000, acc: 0.620, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.001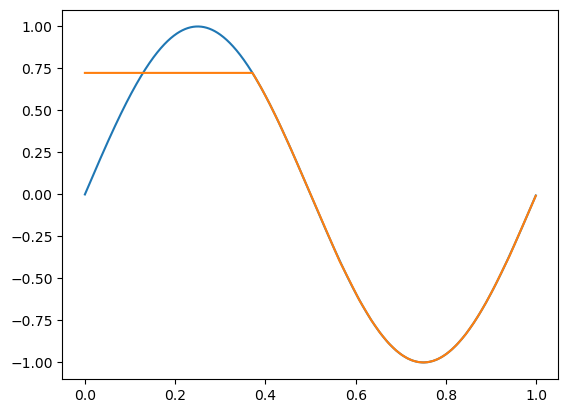
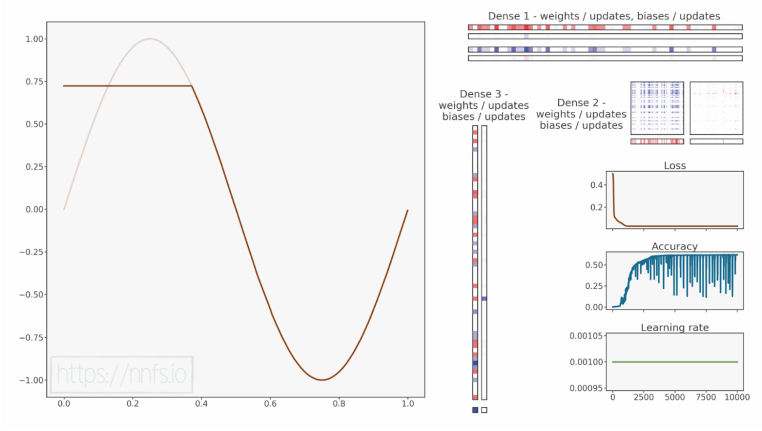
代码可视化:https://nnfs.io/hij
我们的模型准确率并不理想,损失似乎停留在一个较高的水平。从图像中我们可以看到原因,模型在拟合数据时遇到了一些困难,看起来可能卡在了局部最小值。正如我们已经学习过的那样,为了帮助模型跳出局部最小值,我们可以尝试使用更高的学习率并添加学习率衰减。在之前的模型中,我们使用了默认的学习率0.001。现在我们将其设置为0.01,并添加学习率衰减:
python
optimizer = Optimizer_Adam(learning_rate=0.01, decay=1e-3)
python
>>>
epoch: 0, acc: 0.002, loss: 0.500 (data_loss: 0.500, reg_loss: 0.000), lr: 0.01
epoch: 100, acc: 0.027, loss: 0.061 (data_loss: 0.061, reg_loss: 0.000), lr: 0.009099181073703368
...
epoch: 9900, acc: 0.565, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.0009175153683824203
epoch: 10000, acc: 0.564, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.0009091735612328393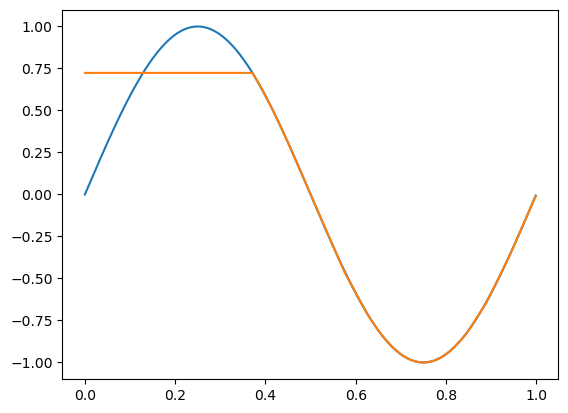
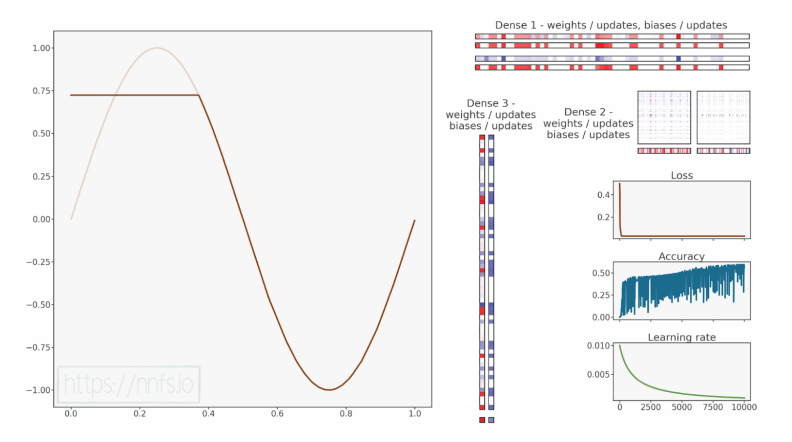
代码可视化:https://nnfs.io/ijk
这次我们的模型似乎仍然停留在更低的准确率上。那就让我们尝试使用更大的学习率吧:
python
optimizer = Optimizer_Adam(learning_rate=0.05, decay=1e-3)
python
>>>
epoch: 0, acc: 0.002, loss: 0.500 (data_loss: 0.500, reg_loss: 0.000), lr: 0.05
epoch: 100, acc: 0.087, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.04549590536851684
...
epoch: 9900, acc: 0.275, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.004587576841912101
epoch: 10000, acc: 0.229, loss: 0.031 (data_loss: 0.031, reg_loss: 0.000), lr: 0.0045458678061641965

代码可视化:https://nnfs.io/jkl
情况变得更加糟糕了。准确率显著下降,我们可以观察到正弦曲线的下部分形状也变得更差了。似乎我们无法让这个模型学习到数据,但经过多次测试和调整超参数后,我们发现学习率设置为0.005时效果更好:
python
optimizer = Optimizer_Adam(learning_rate=0.005, decay=1e-3)
python
>>>
epoch: 0, acc: 0.003, loss: 0.496 (data_loss: 0.496, reg_loss: 0.000), lr: 0.005
epoch: 100, acc: 0.017, loss: 0.048 (data_loss: 0.048, reg_loss: 0.000), lr: 0.004549590536851684
...
epoch: 9900, acc: 0.982, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.00045875768419121016
epoch: 10000, acc: 0.981, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.00045458678061641964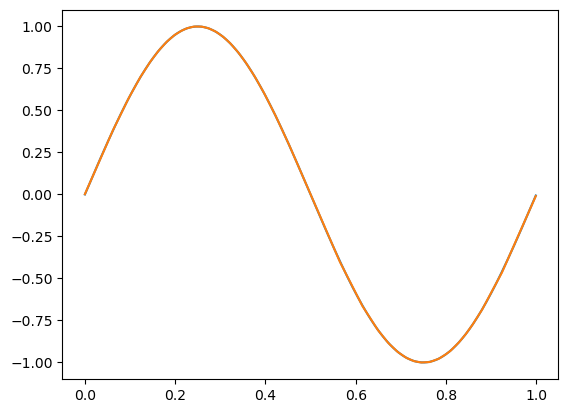
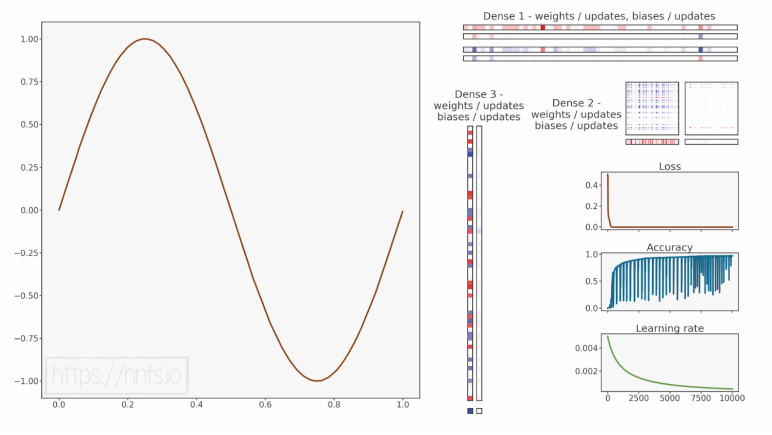
代码可视化:https://nnfs.io/klm
这次模型学习得相当不错,但有趣的是,较低或较高的学习率都会导致准确率较低,并且损失值卡在同一位置,而介于它们之间的学习率反而有效。
调试这种问题通常是一项相当困难的任务,且超出了本书的讨论范围。准确率和损失值表明参数的更新幅度不够大,但增加学习率反而使情况变得更糟,我们只能找到这样一个单一的点,让模型能够学习。你可能还记得,在第3章中,我们讨论了参数初始化方法以及为什么要明智地进行初始化。事实证明,在当前情况下,我们可以通过将Dense层中权重初始化的因子从0.01更改为0.1,来帮助模型学习。但你可能会问------既然学习率用于决定应用到参数的梯度幅度,为什么改变这些初始值会有帮助呢?正如你所记得的,反向传播的梯度是使用权重计算的,而学习率不会影响它。这就是为什么使用正确的权重初始化很重要,而到目前为止,我们为每个模型使用的都是相同的值。
例如,如果我们查看Keras(一个神经网络框架)的源代码,我们会发现:
python
def glorot_uniform(seed=None):
"""Glorot uniform initializer, also called Xavier uniform initializer.
It draws samples from a uniform distribution within [-limit, limit]
where `limit` is `sqrt(6 / (fan_in + fan_out))`
where `fan_in` is the number of input units in the weight tensor
and `fan_out` is the number of output units in the weight tensor.
# Arguments
seed: A Python integer. Used to seed the random generator.
# Returns
An initializer.
# References
Glorot & Bengio, AISTATS 2010
http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
"""
return VarianceScaling(scale=1.,
mode='fan_avg',
distribution='uniform',
seed=seed)这段代码是Keras 2库的一部分。上述内容中真正重要的是注释部分,它描述了如何初始化权重。我们可以发现有一些重要的信息需要记住------用于乘以均匀分布抽取值的因子取决于输入数量和神经元数量,而不像我们的情况那样是一个常数。这种初始化方法称为Glorot均匀分布(Glorot Uniform)。事实上,我们(本书的作者)在自己的项目中也遇到过非常类似的问题,通过改变权重初始化的方式,使模型从完全无法学习变成能够学习的状态。
对于这个模型的目的,让我们将Dense层中权重初始化的正态分布抽取值的乘数因子改为0.1,并重新运行上述四个尝试,比较结果:
python
self.weights = 0.1 * np.random.randn(n_inputs, n_neurons)并重新进行了上述所有测试:
python
optimizer = Optimizer_Adam()
python
>>>
epoch: 0, acc: 0.003, loss: 0.496 (data_loss: 0.496, reg_loss: 0.000), lr: 0.001
epoch: 100, acc: 0.005, loss: 0.114 (data_loss: 0.114, reg_loss: 0.000), lr: 0.001
...
epoch: 9900, acc: 0.869, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.001
epoch: 10000, acc: 0.883, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.001

代码可视化:https://nnfs.io/lmn
这个模型之前被卡住了,现在已经达到了很高的精度。虽然还有一些明显的瑕疵,比如这个正弦曲线的底边,但整体效果较好。
python
optimizer = Optimizer_Adam(learning_rate=0.01, decay=1e-3)
python
>>>
epoch: 0, acc: 0.003, loss: 0.496 (data_loss: 0.496, reg_loss: 0.000), lr: 0.01
epoch: 100, acc: 0.065, loss: 0.011 (data_loss: 0.011, reg_loss: 0.000), lr: 0.009099181073703368
...
epoch: 9900, acc: 0.958, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.0009175153683824203
epoch: 10000, acc: 0.949, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.0009091735612328393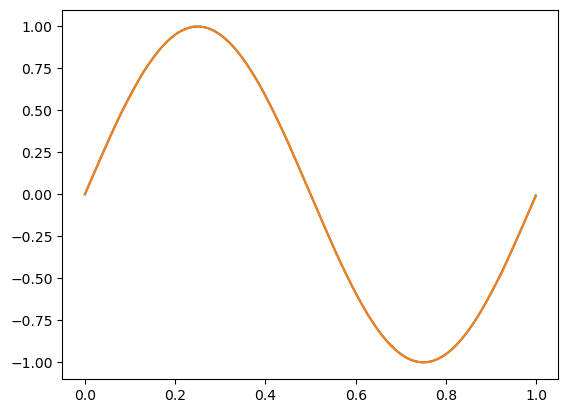
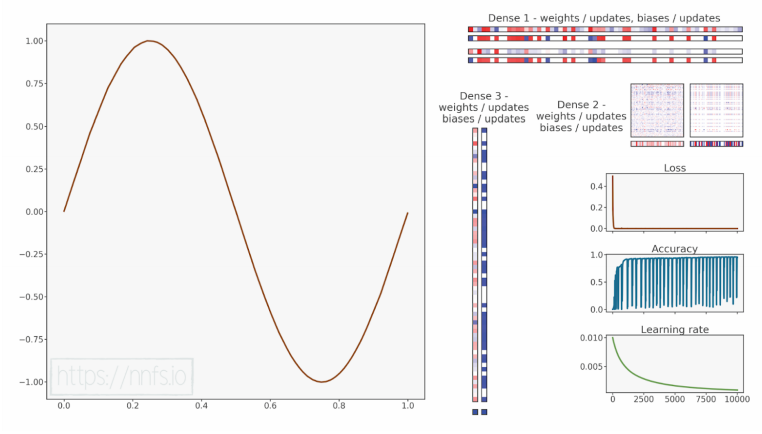
代码可视化:https://nnfs.io/mno
另一个以前被卡住的模型这次训练得非常好,达到了非常高的准确率。
python
optimizer = Optimizer_Adam(learning_rate=0.05, decay=1e-3)
python
>>>
epoch: 0, acc: 0.003, loss: 0.496 (data_loss: 0.496, reg_loss: 0.000), lr: 0.05
epoch: 100, acc: 0.016, loss: 0.008 (data_loss: 0.008, reg_loss: 0.000), lr: 0.04549590536851684
...
epoch: 9000, acc: 0.802, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.005000500050005001
epoch: 9100, acc: 0.233, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004950985246063967
epoch: 9200, acc: 0.434, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004902441415825081
epoch: 9300, acc: 0.838, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.0048548402757549285
epoch: 9400, acc: 0.309, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004808154630252909
epoch: 9500, acc: 0.253, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004762358319839985
epoch: 9600, acc: 0.795, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004717426172280404
epoch: 9700, acc: 0.802, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004673333956444528
epoch: 9800, acc: 0.141, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004630058338735069
epoch: 9900, acc: 0.221, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.004587576841912101
epoch: 10000, acc: 0.631, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.0045458678061641965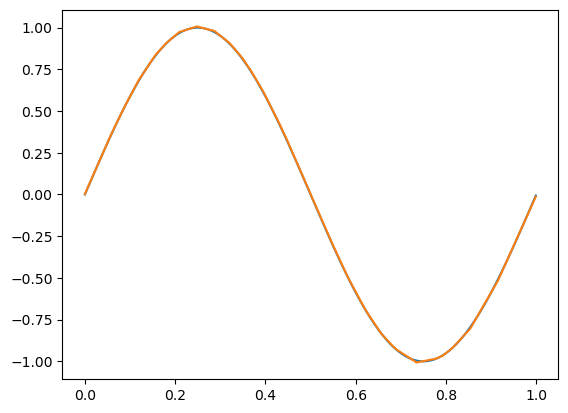
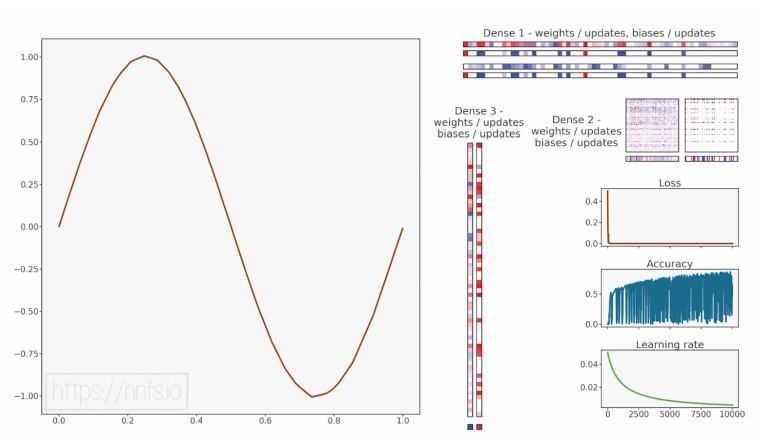
代码可视化:https://nnfs.io/nop
在这种优化器设置下,"跳跃"的准确率表明学习率过大,但即便如此,该模型依然相当不错地学习到了正弦函数的形状。
python
optimizer = Optimizer_Adam(learning_rate=0.005, decay=1e-3)
python
>>>
epoch: 0, acc: 0.003, loss: 0.496 (data_loss: 0.496, reg_loss: 0.000), lr: 0.005
epoch: 100, acc: 0.017, loss: 0.048 (data_loss: 0.048, reg_loss: 0.000), lr: 0.004549590536851684
...
epoch: 9900, acc: 0.982, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.00045875768419121016
epoch: 10000, acc: 0.981, loss: 0.000 (data_loss: 0.000, reg_loss: 0.000), lr: 0.00045458678061641964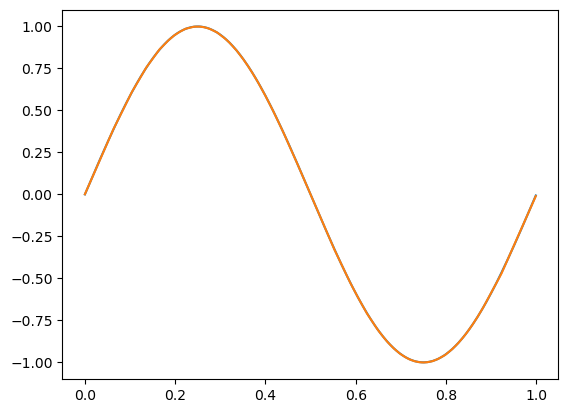
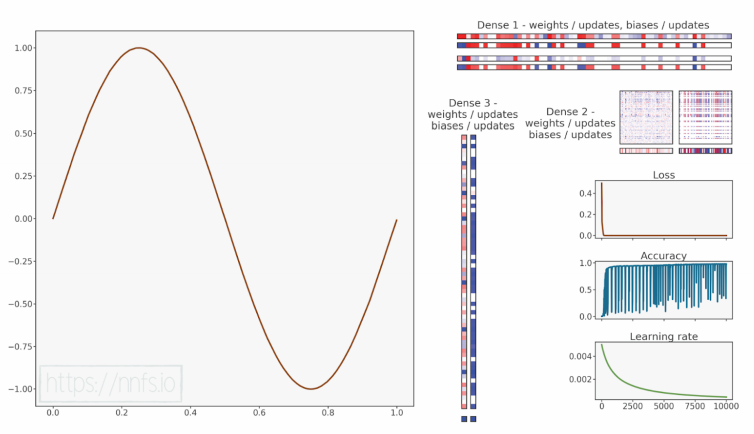
代码可视化:https://nnfs.io/opq
这些超参数再次产生了最佳结果,但差距并不大。
正如我们所看到的,这一次我们的模型在所有情况下都学会了,使用不同的学习率时都没有陷入停滞。这说明改变权重初始化对训练过程的影响是多么显著。
到此为止的全部代码:
python
import numpy as np
import nnfs
from nnfs.datasets import spiral_data
from nnfs.datasets import sine_data
nnfs.init()
# Dense layer
class Layer_Dense:
# Layer initialization
def __init__(self, n_inputs, n_neurons,
weight_regularizer_l1=0, weight_regularizer_l2=0,
bias_regularizer_l1=0, bias_regularizer_l2=0):
# Initialize weights and biases
# self.weights = 0.01 * np.random.randn(n_inputs, n_neurons)
self.weights = 0.1 * np.random.randn(n_inputs, n_neurons)
self.biases = np.zeros((1, n_neurons))
# Set regularization strength
self.weight_regularizer_l1 = weight_regularizer_l1
self.weight_regularizer_l2 = weight_regularizer_l2
self.bias_regularizer_l1 = bias_regularizer_l1
self.bias_regularizer_l2 = bias_regularizer_l2
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs, weights and biases
self.output = np.dot(inputs, self.weights) + self.biases
# Backward pass
def backward(self, dvalues):
# Gradients on parameters
self.dweights = np.dot(self.inputs.T, dvalues)
self.dbiases = np.sum(dvalues, axis=0, keepdims=True)
# Gradients on regularization
# L1 on weights
if self.weight_regularizer_l1 > 0:
dL1 = np.ones_like(self.weights)
dL1[self.weights < 0] = -1
self.dweights += self.weight_regularizer_l1 * dL1
# L2 on weights
if self.weight_regularizer_l2 > 0:
self.dweights += 2 * self.weight_regularizer_l2 * self.weights
# L1 on biases
if self.bias_regularizer_l1 > 0:
dL1 = np.ones_like(self.biases)
dL1[self.biases < 0] = -1
self.dbiases += self.bias_regularizer_l1 * dL1
# L2 on biases
if self.bias_regularizer_l2 > 0:
self.dbiases += 2 * self.bias_regularizer_l2 * self.biases
# Gradient on values
self.dinputs = np.dot(dvalues, self.weights.T)
# Dropout
class Layer_Dropout:
# Init
def __init__(self, rate):
# Store rate, we invert it as for example for dropout
# of 0.1 we need success rate of 0.9
self.rate = 1 - rate
# Forward pass
def forward(self, inputs):
# Save input values
self.inputs = inputs
# Generate and save scaled mask
self.binary_mask = np.random.binomial(1, self.rate, size=inputs.shape) / self.rate
# Apply mask to output values
self.output = inputs * self.binary_mask
# Backward pass
def backward(self, dvalues):
# Gradient on values
self.dinputs = dvalues * self.binary_mask
# ReLU activation
class Activation_ReLU:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Calculate output values from inputs
self.output = np.maximum(0, inputs)
# Backward pass
def backward(self, dvalues):
# Since we need to modify original variable,
# let's make a copy of values first
self.dinputs = dvalues.copy()
# Zero gradient where input values were negative
self.dinputs[self.inputs <= 0] = 0
# Softmax activation
class Activation_Softmax:
# Forward pass
def forward(self, inputs):
# Remember input values
self.inputs = inputs
# Get unnormalized probabilities
exp_values = np.exp(inputs - np.max(inputs, axis=1, keepdims=True))
# Normalize them for each sample
probabilities = exp_values / np.sum(exp_values, axis=1, keepdims=True)
self.output = probabilities
# Backward pass
def backward(self, dvalues):
# Create uninitialized array
self.dinputs = np.empty_like(dvalues)
# Enumerate outputs and gradients
for index, (single_output, single_dvalues) in enumerate(zip(self.output, dvalues)):
# Flatten output array
single_output = single_output.reshape(-1, 1)
# Calculate Jacobian matrix of the output and
jacobian_matrix = np.diagflat(single_output) - np.dot(single_output, single_output.T)
# Calculate sample-wise gradient
# and add it to the array of sample gradients
self.dinputs[index] = np.dot(jacobian_matrix, single_dvalues)
# Sigmoid activation
class Activation_Sigmoid:
# Forward pass
def forward(self, inputs):
# Save input and calculate/save output
# of the sigmoid function
self.inputs = inputs
self.output = 1 / (1 + np.exp(-inputs))
# Backward pass
def backward(self, dvalues):
# Derivative - calculates from output of the sigmoid function
self.dinputs = dvalues * (1 - self.output) * self.output
# Linear activation
class Activation_Linear:
# Forward pass
def forward(self, inputs):
# Just remember values
self.inputs = inputs
self.output = inputs
# Backward pass
def backward(self, dvalues):
# derivative is 1, 1 * dvalues = dvalues - the chain rule
self.dinputs = dvalues.copy()
# SGD optimizer
class Optimizer_SGD:
# Initialize optimizer - set settings,
# learning rate of 1. is default for this optimizer
def __init__(self, learning_rate=1., decay=0., momentum=0.):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.momentum = momentum
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If we use momentum
if self.momentum:
# If layer does not contain momentum arrays, create them
# filled with zeros
if not hasattr(layer, 'weight_momentums'):
layer.weight_momentums = np.zeros_like(layer.weights)
# If there is no momentum array for weights
# The array doesn't exist for biases yet either.
layer.bias_momentums = np.zeros_like(layer.biases)
# Build weight updates with momentum - take previous
# updates multiplied by retain factor and update with
# current gradients
weight_updates = self.momentum * layer.weight_momentums - self.current_learning_rate * layer.dweights
layer.weight_momentums = weight_updates
# Build bias updates
bias_updates = self.momentum * layer.bias_momentums - self.current_learning_rate * layer.dbiases
layer.bias_momentums = bias_updates
# Vanilla SGD updates (as before momentum update)
else:
weight_updates = -self.current_learning_rate * layer.dweights
bias_updates = -self.current_learning_rate * layer.dbiases
# Update weights and biases using either
# vanilla or momentum updates
layer.weights += weight_updates
layer.biases += bias_updates
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adagrad optimizer
class Optimizer_Adagrad:
# Initialize optimizer - set settings
def __init__(self, learning_rate=1., decay=0., epsilon=1e-7):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache += layer.dweights**2
layer.bias_cache += layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# RMSprop optimizer
class Optimizer_RMSprop:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, rho=0.9):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.rho = rho
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_cache = np.zeros_like(layer.biases)
# Update cache with squared current gradients
layer.weight_cache = self.rho * layer.weight_cache + (1 - self.rho) * layer.dweights**2
layer.bias_cache = self.rho * layer.bias_cache + (1 - self.rho) * layer.dbiases**2
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * layer.dweights / (np.sqrt(layer.weight_cache) + self.epsilon)
layer.biases += -self.current_learning_rate * layer.dbiases / (np.sqrt(layer.bias_cache) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Adam optimizer
class Optimizer_Adam:
# Initialize optimizer - set settings
def __init__(self, learning_rate=0.001, decay=0., epsilon=1e-7, beta_1=0.9, beta_2=0.999):
self.learning_rate = learning_rate
self.current_learning_rate = learning_rate
self.decay = decay
self.iterations = 0
self.epsilon = epsilon
self.beta_1 = beta_1
self.beta_2 = beta_2
# Call once before any parameter updates
def pre_update_params(self):
if self.decay:
self.current_learning_rate = self.learning_rate * (1. / (1. + self.decay * self.iterations))
# Update parameters
def update_params(self, layer):
# If layer does not contain cache arrays,
# create them filled with zeros
if not hasattr(layer, 'weight_cache'):
layer.weight_momentums = np.zeros_like(layer.weights)
layer.weight_cache = np.zeros_like(layer.weights)
layer.bias_momentums = np.zeros_like(layer.biases)
layer.bias_cache = np.zeros_like(layer.biases)
# Update momentum with current gradients
layer.weight_momentums = self.beta_1 * layer.weight_momentums + (1 - self.beta_1) * layer.dweights
layer.bias_momentums = self.beta_1 * layer.bias_momentums + (1 - self.beta_1) * layer.dbiases
# Get corrected momentum
# self.iteration is 0 at first pass
# and we need to start with 1 here
weight_momentums_corrected = layer.weight_momentums / (1 - self.beta_1 ** (self.iterations + 1))
bias_momentums_corrected = layer.bias_momentums / (1 - self.beta_1 ** (self.iterations + 1))
# Update cache with squared current gradients
layer.weight_cache = self.beta_2 * layer.weight_cache + (1 - self.beta_2) * layer.dweights**2
layer.bias_cache = self.beta_2 * layer.bias_cache + (1 - self.beta_2) * layer.dbiases**2
# Get corrected cache
weight_cache_corrected = layer.weight_cache / (1 - self.beta_2 ** (self.iterations + 1))
bias_cache_corrected = layer.bias_cache / (1 - self.beta_2 ** (self.iterations + 1))
# Vanilla SGD parameter update + normalization
# with square rooted cache
layer.weights += -self.current_learning_rate * weight_momentums_corrected / (np.sqrt(weight_cache_corrected) + self.epsilon)
layer.biases += -self.current_learning_rate * bias_momentums_corrected / (np.sqrt(bias_cache_corrected) + self.epsilon)
# Call once after any parameter updates
def post_update_params(self):
self.iterations += 1
# Common loss class
class Loss:
# Regularization loss calculation
def regularization_loss(self, layer):
# 0 by default
regularization_loss = 0
# L1 regularization - weights
# calculate only when factor greater than 0
if layer.weight_regularizer_l1 > 0:
regularization_loss += layer.weight_regularizer_l1 * np.sum(np.abs(layer.weights))
# L2 regularization - weights
if layer.weight_regularizer_l2 > 0:
regularization_loss += layer.weight_regularizer_l2 * np.sum(layer.weights * layer.weights)
# L1 regularization - biases
# calculate only when factor greater than 0
if layer.bias_regularizer_l1 > 0:
regularization_loss += layer.bias_regularizer_l1 * np.sum(np.abs(layer.biases))
# L2 regularization - biases
if layer.bias_regularizer_l2 > 0:
regularization_loss += layer.bias_regularizer_l2 * np.sum(layer.biases * layer.biases)
return regularization_loss
# Calculates the data and regularization losses
# given model output and ground truth values
def calculate(self, output, y):
# Calculate sample losses
sample_losses = self.forward(output, y)
# Calculate mean loss
data_loss = np.mean(sample_losses)
# Return loss
return data_loss
# Cross-entropy loss
class Loss_CategoricalCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Number of samples in a batch
samples = len(y_pred)
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Probabilities for target values -
# only if categorical labels
if len(y_true.shape) == 1:
correct_confidences = y_pred_clipped[
range(samples),
y_true
]
# Mask values - only for one-hot encoded labels
elif len(y_true.shape) == 2:
correct_confidences = np.sum(y_pred_clipped * y_true, axis=1)
# Losses
negative_log_likelihoods = -np.log(correct_confidences)
return negative_log_likelihoods
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of labels in every sample
# We'll use the first sample to count them
labels = len(dvalues[0])
# If labels are sparse, turn them into one-hot vector
if len(y_true.shape) == 1:
y_true = np.eye(labels)[y_true]
# Calculate gradient
self.dinputs = -y_true / dvalues
# Normalize gradient
self.dinputs = self.dinputs / samples
# Binary cross-entropy loss
class Loss_BinaryCrossentropy(Loss):
# Forward pass
def forward(self, y_pred, y_true):
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
y_pred_clipped = np.clip(y_pred, 1e-7, 1 - 1e-7)
# Calculate sample-wise loss
sample_losses = -(y_true * np.log(y_pred_clipped) + (1 - y_true) * np.log(1 - y_pred_clipped))
sample_losses = np.mean(sample_losses, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Clip data to prevent division by 0
# Clip both sides to not drag mean towards any value
clipped_dvalues = np.clip(dvalues, 1e-7, 1 - 1e-7)
# Calculate gradient
self.dinputs = -(y_true / clipped_dvalues - (1 - y_true) / (1 - clipped_dvalues)) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Squared Error loss
class Loss_MeanSquaredError(Loss): # L2 loss
# Forward pass
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean((y_true - y_pred)**2, axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Gradient on values
self.dinputs = -2 * (y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Mean Absolute Error loss
class Loss_MeanAbsoluteError(Loss): # L1 loss
def forward(self, y_pred, y_true):
# Calculate loss
sample_losses = np.mean(np.abs(y_true - y_pred), axis=-1)
# Return losses
return sample_losses
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# Number of outputs in every sample
# We'll use the first sample to count them
outputs = len(dvalues[0])
# Calculate gradient
self.dinputs = np.sign(y_true - dvalues) / outputs
# Normalize gradient
self.dinputs = self.dinputs / samples
# Softmax classifier - combined Softmax activation
# and cross-entropy loss for faster backward step
class Activation_Softmax_Loss_CategoricalCrossentropy():
# Creates activation and loss function objects
def __init__(self):
self.activation = Activation_Softmax()
self.loss = Loss_CategoricalCrossentropy()
# Forward pass
def forward(self, inputs, y_true):
# Output layer's activation function
self.activation.forward(inputs)
# Set the output
self.output = self.activation.output
# Calculate and return loss value
return self.loss.calculate(self.output, y_true)
# Backward pass
def backward(self, dvalues, y_true):
# Number of samples
samples = len(dvalues)
# If labels are one-hot encoded,
# turn them into discrete values
if len(y_true.shape) == 2:
y_true = np.argmax(y_true, axis=1)
# Copy so we can safely modify
self.dinputs = dvalues.copy()
# Calculate gradient
self.dinputs[range(samples), y_true] -= 1
# Normalize gradient
self.dinputs = self.dinputs / samples
# Create dataset
X, y = sine_data()
# Create Dense layer with 1 input feature and 64 output values
dense1 = Layer_Dense(1, 64)
# Create ReLU activation (to be used with Dense layer):
activation1 = Activation_ReLU()
# Create second Dense layer with 64 input features (as we take output
# of previous layer here) and 64 output values
dense2 = Layer_Dense(64, 64)
# Create ReLU activation (to be used with Dense layer):
activation2 = Activation_ReLU()
# Create third Dense layer with 64 input features (as we take output
# of previous layer here) and 1 output value
dense3 = Layer_Dense(64, 1)
# Create Linear activation:
activation3 = Activation_Linear()
# Create loss function
loss_function = Loss_MeanSquaredError()
# Create optimizer
# optimizer = Optimizer_Adam()
# optimizer = Optimizer_Adam(learning_rate=0.01, decay=1e-3)
# optimizer = Optimizer_Adam(learning_rate=0.05, decay=1e-3)
optimizer = Optimizer_Adam(learning_rate=0.005, decay=1e-3)
# Accuracy precision for accuracy calculation
# There are no really accuracy factor for regression problem,
# but we can simulate/approximate it. We'll calculate it by checking
# how many values have a difference to their ground truth equivalent
# less than given precision
# We'll calculate this precision as a fraction of standard deviation
# of al the ground truth values
accuracy_precision = np.std(y) / 250
# Train in loop
for epoch in range(10001):
# Perform a forward pass of our training data through this layer
dense1.forward(X)
# Perform a forward pass through activation function
# takes the output of first dense layer here
activation1.forward(dense1.output)
# Perform a forward pass through second Dense layer
# takes outputs of activation function
# of first layer as inputs
dense2.forward(activation1.output)
# Perform a forward pass through activation function
# takes the output of second dense layer here
activation2.forward(dense2.output)
# Perform a forward pass through third Dense layer
# takes outputs of activation function of second layer as inputs
dense3.forward(activation2.output)
# Perform a forward pass through activation function
# takes the output of third dense layer here
activation3.forward(dense3.output)
# Calculate the data loss
data_loss = loss_function.calculate(activation3.output, y)
# Calculate regularization penalty
regularization_loss = loss_function.regularization_loss(dense1) + loss_function.regularization_loss(dense2) + loss_function.regularization_loss(dense3)
# Calculate overall loss
loss = data_loss + regularization_loss
# Calculate accuracy from output of activation2 and targets
# To calculate it we're taking absolute difference between
# predictions and ground truth values and compare if differences
# are lower than given precision value
predictions = activation3.output
accuracy = np.mean(np.absolute(predictions - y) <
accuracy_precision)
if not epoch % 100:
print(f'epoch: {epoch}, ' +
f'acc: {accuracy:.3f}, ' +
f'loss: {loss:.3f} (' +
f'data_loss: {data_loss:.3f}, ' +
f'reg_loss: {regularization_loss:.3f}), ' +
f'lr: {optimizer.current_learning_rate}')
# Backward pass
loss_function.backward(activation3.output, y)
activation3.backward(loss_function.dinputs)
dense3.backward(activation3.dinputs)
activation2.backward(dense3.dinputs)
dense2.backward(activation2.dinputs)
activation1.backward(dense2.dinputs)
dense1.backward(activation1.dinputs)
# Update weights and biases
optimizer.pre_update_params()
optimizer.update_params(dense1)
optimizer.update_params(dense2)
optimizer.update_params(dense3)
optimizer.post_update_params()
import matplotlib.pyplot as plt
X_test, y_test = sine_data()
dense1.forward(X_test)
activation1.forward(dense1.output)
dense2.forward(activation1.output)
activation2.forward(dense2.output)
dense3.forward(activation2.output)
activation3.forward(dense3.output)
plt.plot(X_test, y_test)
plt.plot(X_test, activation3.output)
plt.show()本章的章节代码、更多资源和勘误表:https://nnfs.io/ch17