目录
- 0 专栏介绍
- 1 从路径到轨迹
- 2 基于贝塞尔曲线的粗轨迹生成
-
- 2.1 路径关键点提取
- 2.2 路径点航向角计算
- 2.3 贝塞尔曲线轨迹生成
- 3 算法仿真
-
- 3.1 ROS C++仿真
- 3.2 Python仿真
0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
1 从路径到轨迹
路径规划和轨迹生成是自主导航和机器人控制中的两个关键步骤,它们虽然相关,但有着不同的目的和功能。
路径规划的目的是找到从起点到终点的一条可行路径,通常是在已知环境中进行。路径规划算法考虑的是全局的几何路径,不关心时间和动态特性,其输出通常是一个离散的路径点集合,这些点表示机器人在空间中的位置 { x , y , z } \{x,y,z\} {x,y,z}。
轨迹生成是在路径规划的基础上,为机器人生成一条平滑、可执行的轨迹。轨迹生成不仅考虑空间上的位置,还包括时间、速度、加速度等动态特性。轨迹生成的目的是确保机器人沿着路径点运动时,速度和加速度都是可控和安全的。轨迹的相关参数包括
{ x , y , z , θ , t , v , a , j e r k , . . . } \{x,y,z,\theta ,t,v,a,jerk, ...\} {x,y,z,θ,t,v,a,jerk,...}
在优化问题中,使用轨迹进行优化比单纯用路径进行优化有诸多优势。具体而言,轨迹同时包含静态和动态的丰富信息,且通常连续可微,因此可以方便地对轨迹设计目标函数,添加速度、加速度等动态约束,进一步生成符合物理特性的轨迹。
本节介绍的基于贝塞尔曲线的粗轨迹生成模块主要用于将上游规划的离散路径点转为连续的多项式轨迹,为进一步的轨迹优化做准备。
2 基于贝塞尔曲线的粗轨迹生成
2.1 路径关键点提取
本节采用路径处理 | 关键点提取之Douglas--Peucker算法(附ROS C++/Python实现)的**道格拉斯-普克算法(Douglas--Peucker)**提取路径关键点,在保留路径关键特征和形状的基础上滤除噪点,使生成的轨迹更稳定、更平滑

剪枝前(红色点表示路径点)

剪枝后(红色点表示路径点)
2.2 路径点航向角计算
经过2.1节的路径预处理,得到二维离散路点 { x i , y i } ( i = 1 , . . . , N ) \{x_i,y_i\}(i=1,...,N) {xi,yi}(i=1,...,N)。默认状态下,除了用户给定的起始点和终点外,其余的路点来自路径规划算法的结果,并没有朝向角的定义,而路点的朝向对于机器人运动而言至关重要。
本节通过简单的几何学原理赋予路点方向。具体地,根据三点共圆的性质,可以计算每三个点 p 1 \boldsymbol{p}_1 p1、 p 2 \boldsymbol{p}_2 p2、 p 3 \boldsymbol{p}_3 p3所在圆的圆心坐标 c \boldsymbol{c} c
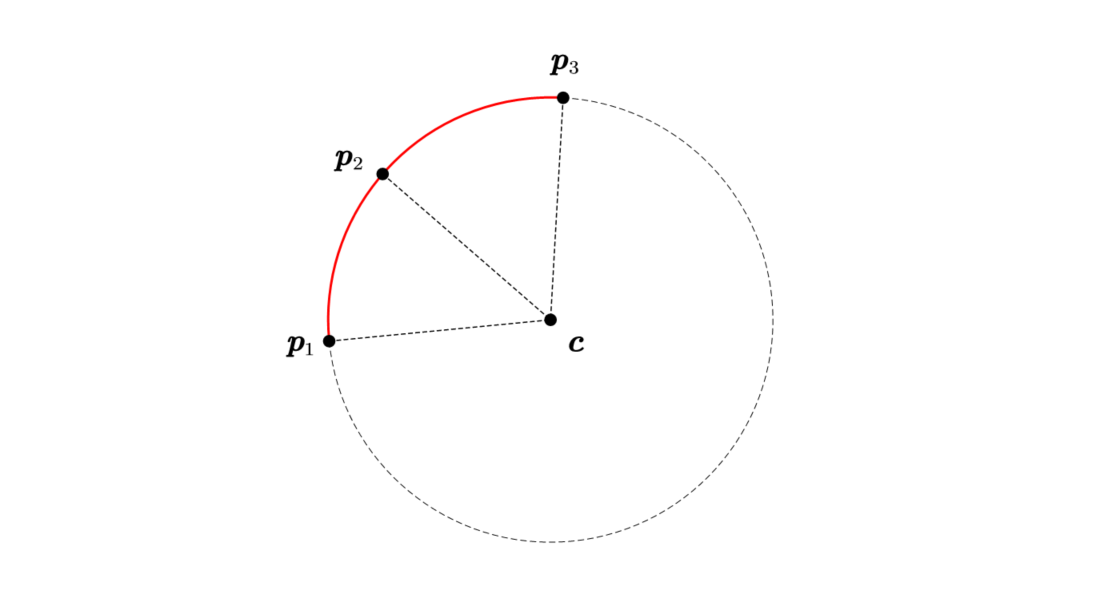
取向量 p 2 c \boldsymbol{p_2c} p2c的法向量即为路点 p 2 \boldsymbol{p}_2 p2的朝向
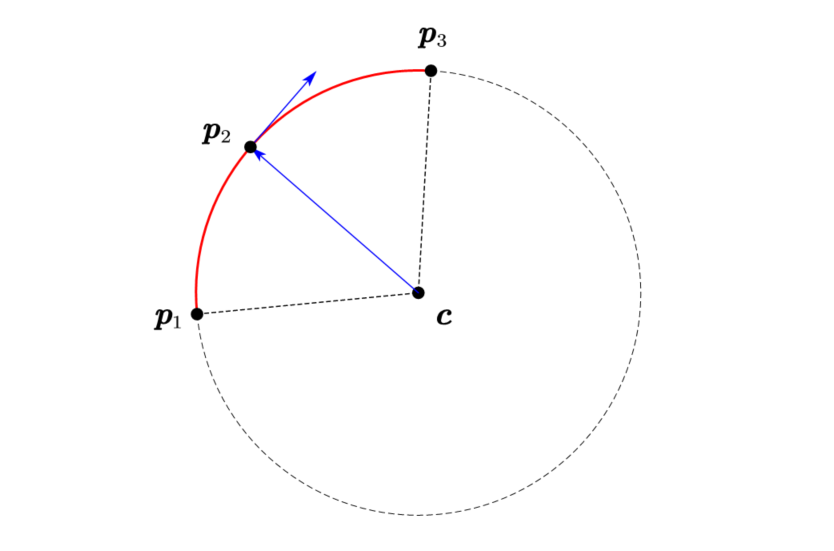
由于首末路点的朝向给定,所以通过该算法可以确定路径上每个位置的方向
2.3 贝塞尔曲线轨迹生成
贝塞尔曲线是一种数学曲线,由法国数学家皮埃尔·贝塞尔于1962年引入。它使用一组控制点来定义曲线的形状,这些控制点的位置和数量决定了曲线的特征。贝塞尔曲线因为其凸包性、端点性等优良性质被广泛应用于机器人运动规划中,其具体的原理请看曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
在贝塞尔曲线中,通过相邻两个路径点及其朝向,可以启发式地定义两个控制点。在四个点的约束下,本节选用三次贝塞尔曲线进行轨迹插值
p = [ ( p 3 − p 0 ) − 3 ( p 2 − p 1 ) ] t 3 + [ 3 ( p 2 − p 1 ) − 3 ( p 1 − p 0 ) ] t 2 + 3 ( p 1 − p 0 ) t + p 0 \begin{aligned}\boldsymbol{p}&=[(\boldsymbol{p_3}-\boldsymbol{p_0})-3(\boldsymbol{p_2}-\boldsymbol{p_1})]t^3 \\ &+[3(\boldsymbol{p_2}-\boldsymbol{p_1})-3(\boldsymbol{p_1}-\boldsymbol{p_0})]t^2 \\ &+3(\boldsymbol{p_1}-\boldsymbol{p_0})t \\&+\boldsymbol{p_0}\end{aligned} p=[(p3−p0)−3(p2−p1)]t3+[3(p2−p1)−3(p1−p0)]t2+3(p1−p0)t+p0

3 算法仿真
3.1 ROS C++仿真
核心代码如下所示
cpp
for (size_t i = 1; i <= waypoints_.size(); i++)
{
if ((!std::isinf(prelast_dir.x())) && (!std::isinf(prelast_dir.y())))
{
...
// Interpolate poses between prelast and last
auto prelast_pt = Point3d(waypoints_[i - 2].x(), waypoints_[i - 2].y(), prelast_dir.angle());
auto last_pt = Point3d(waypoints_[i - 1].x(), waypoints_[i - 1].y(), last_dir.angle());
auto interp_pts = bezier_gen_->generation(prelast_pt, last_pt);
// Assign orientations to interpolated points
trajectory_.position.emplace_back(prelast_pt);
if (interp_pts.size() > 0)
{
for (size_t j = 1; j < interp_pts.size() - 1; j++)
{
auto prev_interp_vec = Vec2d(interp_pts[j - 1].x(), interp_pts[j - 1].y());
auto curr_interp_vec = Vec2d(interp_pts[j].x(), interp_pts[j].y());
auto next_interp_vec = Vec2d(interp_pts[j + 1].x(), interp_pts[j + 1].y());
auto tangent_dir = rmp::common::math::tangentDir(prev_interp_vec, curr_interp_vec, next_interp_vec, false);
auto dir = tangent_dir.innerProd(curr_interp_vec - prev_interp_vec) >= 0 ? tangent_dir : -tangent_dir;
trajectory_.position.emplace_back(interp_pts[j].x(), interp_pts[j].y(), dir.angle());
}
}
trajectory_.position.emplace_back(last_pt);
prelast_dir = last_dir;
}
3.2 Python仿真
核心代码如下所示
python
for i in range(1, len(waypoints) + 1):
if prelast_dir is not None:
last_dir = Vec2d()
prelast = Vec2d(waypoints[i - 2].x(), waypoints[i - 2].y())
last = Vec2d(waypoints[i - 1].x(), waypoints[i - 1].y())
# Compute orientation of last
if i < len(waypoints):
current = Vec2d(waypoints[i].x(), waypoints[i].y())
tangent_dir = MathHelper.tangentDir(prelast, last, current)
last_dir = tangent_dir if tangent_dir.innerProduct(current - last) >= 0 else -tangent_dir
last_dir.normalize()
elif self.keep_goal_orientation:
last_dir = goal_dir
else:
last_dir = last - prelast
last_dir.normalize()
last_angle = last_dir.angle()
# Interpolate poses between prelast and last
prelast_pt, last_pt = waypoints[i - 2], waypoints[i - 1]
prelast_pt.setTheta(prelast_dir.angle())
last_pt.setTheta(last_dir.angle())
interp_pts, _ = self.traj_gen.generation(prelast_pt, last_pt)
interp_cnt = len(interp_pts)
self.trajectory += interp_pts
# Assign orientations to interpolated points
traj_size = len(self.trajectory)
for j in range(traj_size - 1 - interp_cnt, traj_size - 1):
tangent_dir = MathHelper.tangentDir(
Vec2d(self.trajectory[j - 1].x(), self.trajectory[j - 1].y()),
Vec2d(self.trajectory[j].x(), self.trajectory[j].y()),
Vec2d(self.trajectory[j + 1].x(), self.trajectory[j + 1].y())
)
self.trajectory[j].setTheta(tangent_dir.angle())
prelast_dir = last_dir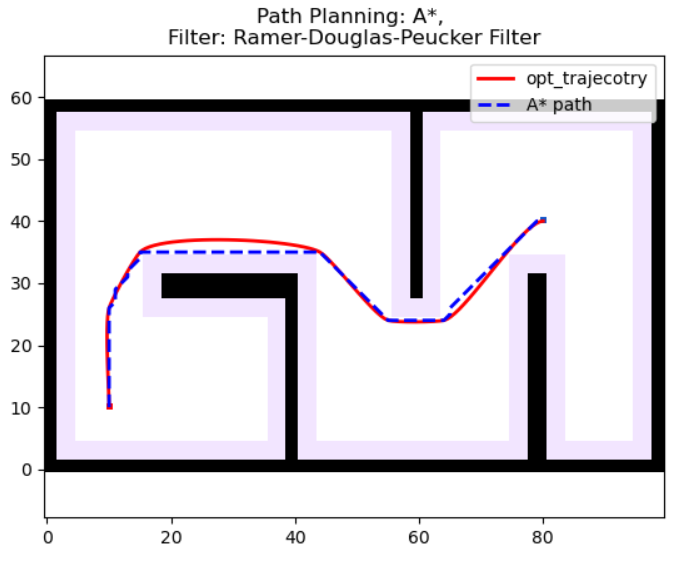
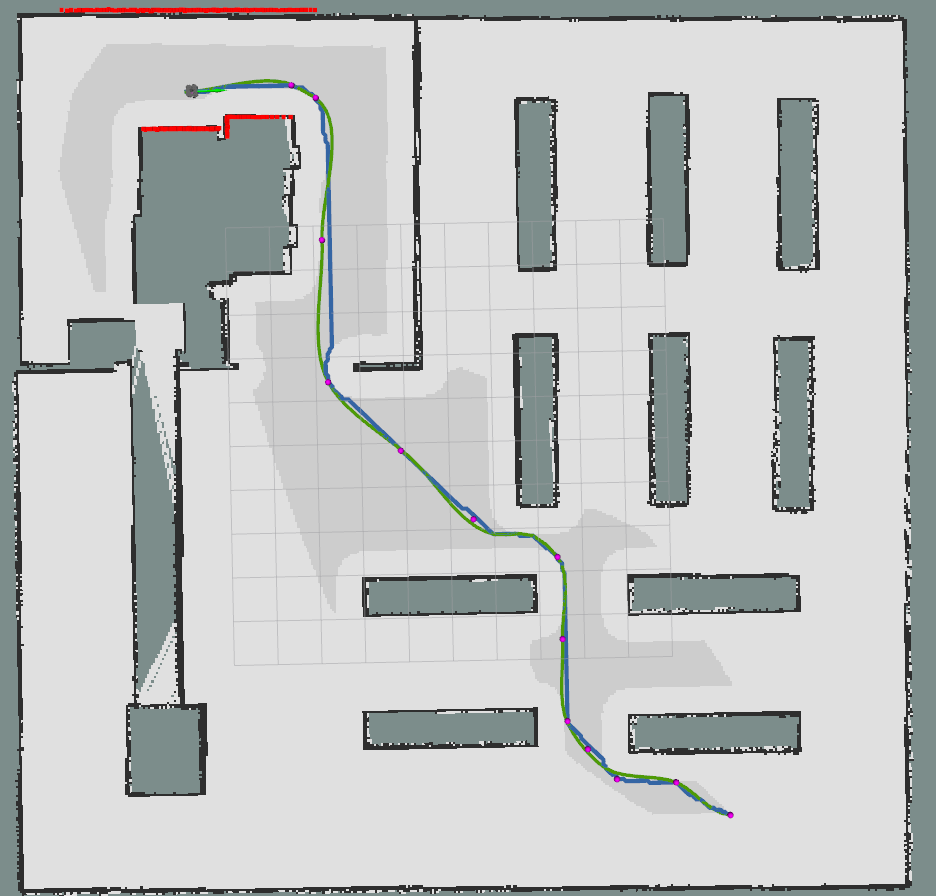
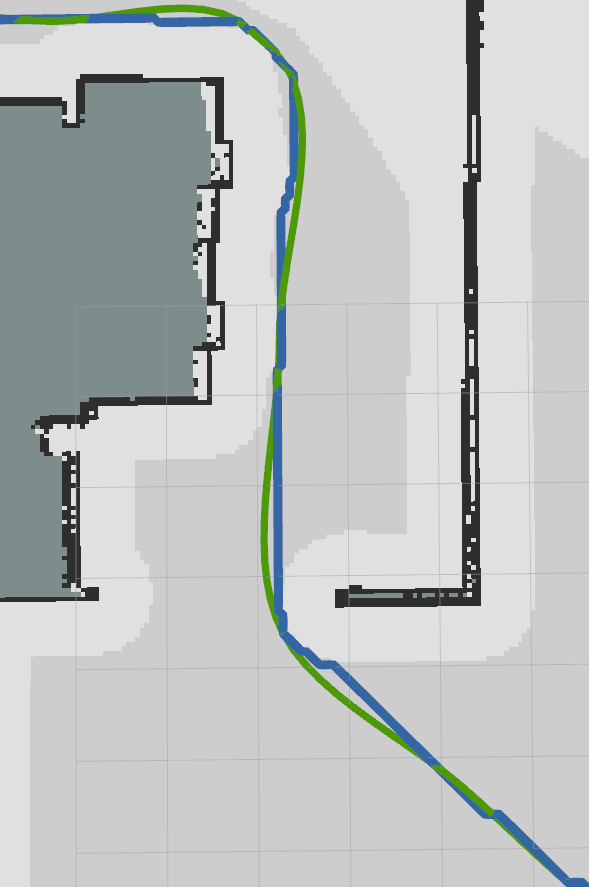
可视化轨迹点和关键点朝向

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇