[Computer Vision]实验三：图像拼接

一、实验内容

二、实验过程及结果

[2.1 单应性变换](#2.1 单应性变换)

[2.2 RANSAC算法](#2.2 RANSAC算法)

三、实验小结

一、实验内容

理解单应性变换中各种变换的原理（自由度），并实现图像平移、旋转、仿射变换等操作，输出对应的单应性矩阵。
利用RANSAC算法优化关键点匹配，比较优化前后图像拼接和所生成全景图的差别，输出RANSAC前后匹配点数量、单应性矩阵。

二、实验过程及结果

2.1 单应性变换

（1）实验代码

python 复制代码

import cv2
from networkx import center
import numpy as np
from scipy.fft import dst
import matplotlib.pyplot as plt
img=cv2.imread("D:/Computer vision/test1 picture/picture3.png")

x=100
y=50
M0=np.float32([[1,0,x],[0,1,y]])
translated=cv2.warpAffine(img,M0,(img.shape[1],img.shape[0]))
print("平移变换单应性矩阵：\n",M0)

img_center=(img.shape[1]/2,img.shape[0]/2)
M1=cv2.getRotationMatrix2D(img_center,45,1)
rotated=cv2.warpAffine(img,M1,(img.shape[1],img.shape[0]))
print("旋转变换单应性矩阵：\n",M1)

M2=cv2.getRotationMatrix2D(img_center,0,0.5)
scaled=cv2.warpAffine(img,M2,(img.shape[1],img.shape[0]))
print("缩放变换单应性矩阵：\n",M2)

rows,cols,ch=img.shape
src_points=np.float32([[0,0],[cols-1,0],[0,rows-1]])
dst_points=np.float32([[0,rows*0.33],[cols*0.85,rows*0.25],[cols*0.15,rows*0.7]])
M3=cv2.getAffineTransform(src_points,dst_points)
warped=cv2.warpAffine(img,M3,(cols,rows))
print("扭曲变换单应性矩阵：\n",M3)

rows,cols=img.shape[:2]
pts1=np.float32([[150,50],[400,50],[60,450],[310,450]])
pts2=np.float32([[50,50],[rows-50,50],[50,cols-50],[rows-50,cols-50]])
M4=cv2.getPerspectiveTransform(pts1,pts2)
img_dst=cv2.warpPerspective(img,M4,(cols,rows))
print("透视变换单应性矩阵：\n",M4)

plt.figure("Processed Images")
plt.subplot(2,3,1)
plt.imshow(img)
plt.title("Original Image")
plt.subplot(2,3,2)
plt.imshow(translated)
plt.title("Translated Image")
plt.subplot(2,3,3)
plt.imshow(rotated)
plt.title("Rotated Image")
plt.subplot(2,3,4)
plt.imshow(scaled)
plt.title("Scaled Image")
plt.subplot(2,3,5)
plt.imshow(warped)
plt.title("Warped Image")
plt.subplot(2,3,6)
plt.imshow(img_dst)
plt.title("Dst Image")
plt.show()
plt.savefig("D:/Computer vision/ransac_picture/processed_images.png")
plt.show()

（2）实验结果截图

图1为输出的单应性矩阵结果截图：

平移变换：两个自由度（两个平移参数），单应性矩阵为2*3的矩阵

旋转变换：一个自由度（一个旋转角度参数），单应性矩阵为2*3的矩阵

缩放变换：一个自由度（一个缩放因子），单应性矩阵为2*3的矩阵

扭曲变换有六个自由度（两个旋转参数一个缩放因子），单应性矩阵为2*3的矩阵

透视变换有八个自由度（5个是仿射变换参数，3个是透视变换参数），单应性矩阵为3*3的矩阵
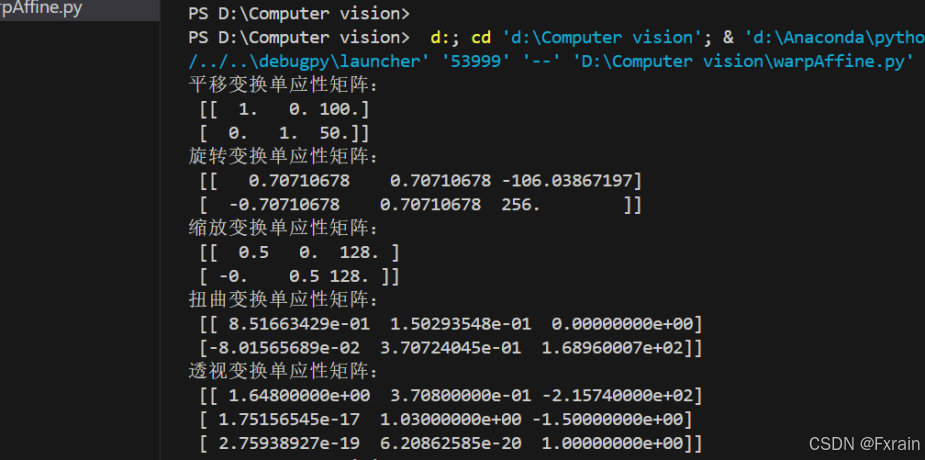图1

图2为输出的单应性变换的结果图：

可以看到，平移变换的图像在x方向上平移100个像素,在y方向上平移50个像素。旋转变换的图像绕图像中心旋转45度。缩放变换的图像在x方向上缩小到原来的一半，在y方向上缩小到原来的一半。扭曲变换的图像进行仿射变换，包括旋转、缩放、平移和剪切。透视变换的图像进行了透视变换，包括旋转、缩放、平移和透视变形。
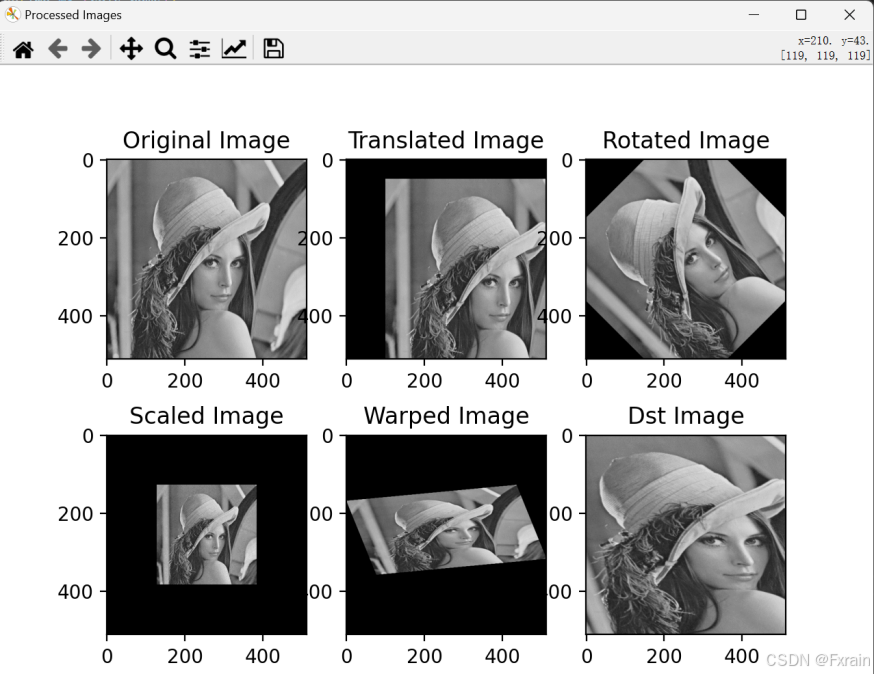图2

2.2 RANSAC算法

（1）实验代码

python 复制代码

import cv2
import numpy as np

def detectAndCompute(image):
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    sift = cv2.SIFT_create()
    keypoints, descriptors = sift.detectAndCompute(gray, None)
    return keypoints, descriptors

def matchKeyPoints(kpsA, kpsB, featuresA, featuresB, ratio=0.75, reprojThresh=4.0):
    matcher = cv2.BFMatcher()
    rawMatches = matcher.knnMatch(featuresA, featuresB, 2)
    matches = []
    for m in rawMatches:
        if len(m) == 2 and m[0].distance < ratio * m[1].distance:
            matches.append((m[0].queryIdx, m[0].trainIdx))
    ptsA = np.float32([kpsA[i].pt for (i, _) in matches])
    ptsB = np.float32([kpsB[i].pt for (_, i) in matches])
    (M, status) = cv2.findHomography(ptsA, ptsB, cv2.RANSAC, reprojThresh)
    return (M, matches, status)

def drawMatches(imgA, imgB, kpsA, kpsB, matches, status):
    (hA, wA) = imgA.shape[:2]
    (hB, wB) = imgB.shape[:2]
    result = np.zeros((max(hA, hB), wA + wB, 3), dtype="uint8")
    result[0:hA, 0:wA] = imgA
    result[0:hB, wA:] = imgB
    for ((trainIdx, queryIdx), s) in zip(matches, status):
        if s == 1:
            ptA = (int(kpsA[queryIdx].pt[0]), int(kpsA[queryIdx].pt[1]))
            ptB = (int(kpsB[trainIdx].pt[0]) + wA, int(kpsB[trainIdx].pt[1]))
            cv2.line(result, ptA, ptB, (0, 255, 0), 1)
    return result

def stitchImages(imageA, imageB, M):
    (hA, wA) = imageA.shape[:2]
    (hB, wB) = imageB.shape[:2]
    result = cv2.warpPerspective(imageA, M, (wA + wB, hA))
    result[0:hB, 0:wB] = imageB
    return result

if __name__ == '__main__':
    imageA = cv2.imread("D:\Computer vision/ransac_picture/ransac1.jpg")
    imageB = cv2.imread("D:/Computer vision/ransac_picture/ransac2.jpg")
    
    kpsA, featuresA = detectAndCompute(imageA)
    kpsB, featuresB = detectAndCompute(imageB)
    
    M, matches, status = matchKeyPoints(kpsA, kpsB, featuresA, featuresB)
    
    initial_matches = sum(status)
    final_matches = len(matches)
    print(f"RANSAC前匹配点数量: {initial_matches}")
    print(f"RANSAC后匹配点数量: {final_matches}")
    print("单应性矩阵为:\n", M)
    
    drawImgBeforeRANSAC = drawMatches(imageA, imageB, kpsA, kpsB, matches, status)
    cv2.imshow("drawMatches Before RANSAC", drawImgBeforeRANSAC)
    cv2.waitKey()
    cv2.destroyAllWindows()

    stitchedImage = stitchImages(imageA, imageB, M)
    cv2.imshow("Stitched Image", stitchedImage)
    cv2.waitKey()
    cv2.destroyAllWindows()
    cv2.imwrite("D:/Computer vision/ransac_picture/stitched_image.jpg", stitchedImage)
cv2.imwrite("D:/Computer vision/ransac_picture/drawMatchesBeforeRANSAC.jpg", drawImgBeforeRANSAC)

（2）数据集(待拼接)

（3）实验结果截图

图3为输出的单应性矩阵结果截图：

如图所示，在运行SIFT特征检测和描述符提取后，通过BFMatcher进行特征匹配，初始匹配点的数量是198对。经过RANSAC算法去除错误匹配后，剩余的匹配点数量为1074对。这表明RANSAC算法有效地保留了正确的匹配点并去除了错误的匹配点。
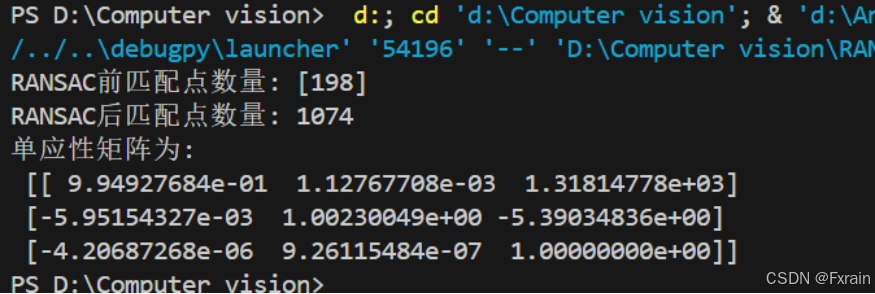图3

图4为在应用RANSAC算法之前绘制的匹配结果图像：

如图所示，绘制两幅图像的匹配结果并显示特征点之间的匹配关系。通过可视化匹配结果，可以直观地看到哪些特征点被成功匹配。
图4

图5为最终拼接后的图像：
图5

三、实验小结

图像拼接是计算机视觉领域的一个重要研究方向，通过将多张重叠的图像拼接在一起，实现更大、更全面的图像展示。实验中通过使用opencv中的相关函数实现图像的单应性变换，并使用BFMatcher和RANSAC算法进行了特征点匹配以及图像拼接。使用RANSAC算法后拼接效果良好，没有出现明显的错位或重叠问题。