卷积神经网络是计算机视觉领域的核心架构,其能力源于通过反向传播算法从数据中自动学习特征的能力。本文将深入探讨卷积层中反向传播的数学原理,揭示网络如何通过梯度下降调整卷积核参数。
一、前向传播:从输入到损失
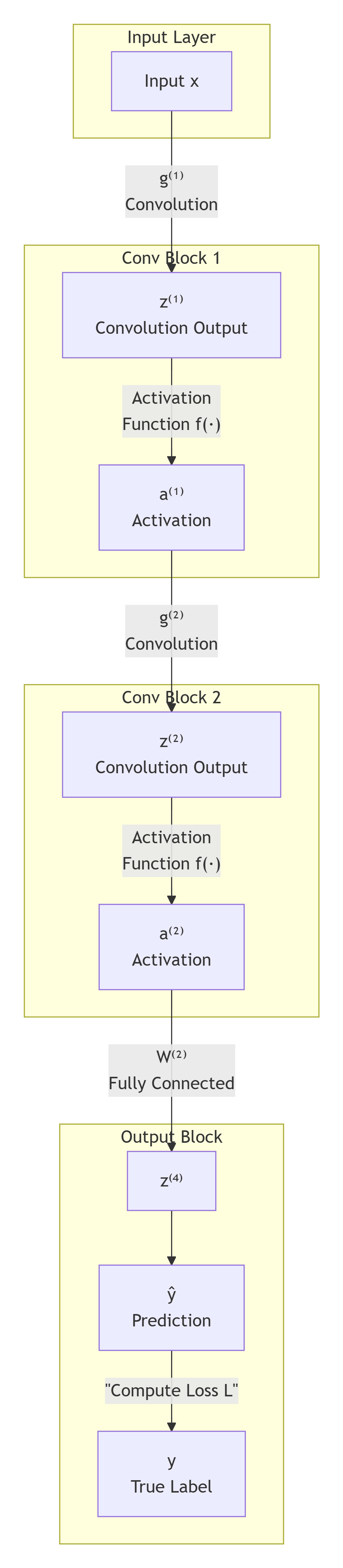
一个典型的卷积网络由多个卷积层、激活函数和池化层交替构成。前向传播过程可以简化为:
输入图像 → 卷积运算 → 激活函数 → 下一层卷积 → ... → 输出预测 → 计算损失
用数学符号表示第l层的前向传播:
- 卷积输出:z(l)=a(l−1)∗g(l)z^{(l)} = a^{(l-1)} \ast g^{(l)}z(l)=a(l−1)∗g(l)(其中∗\ast∗表示卷积运算)
- 激活输出:a(l)=f(z(l))a^{(l)} = f(z^{(l)})a(l)=f(z(l))(f为ReLU等激活函数)
最终,网络输出与真实标签之间的差异被损失函数LLL量化,这是整个学习过程的驱动力量。
二、反向传播:梯度的逆向流动
反向传播的核心任务是计算损失函数对每个参数的梯度,即∂L∂g(l)\frac{\partial L}{\partial g^{(l)}}∂g(l)∂L。这是通过链式法则从输出层向输入层逐层传递误差信号实现的。
2.1 误差信号的反向传递
损失函数对第l层卷积输出的梯度计算为:
∂L∂zij(l)=(∑m=0M∑n=0Ngmn(l)∂L∂z(i+m)(j+n)(l+1))∂f(zij(l))∂zij(l)\frac{\partial L}{\partial z_{ij}^{(l)}} = \left( \sum_{m=0}^{M} \sum_{n=0}^{N} g_{mn}^{(l)} \frac{\partial L}{\partial z_{(i+m)(j+n)}^{(l+1)}} \right) \frac{\partial f(z_{ij}^{(l)})}{\partial z_{ij}^{(l)}}∂zij(l)∂L= m=0∑Mn=0∑Ngmn(l)∂z(i+m)(j+n)(l+1)∂L ∂zij(l)∂f(zij(l))
这个公式包含两个关键部分:
- 误差分配 :通过卷积核权重将下一层的误差∂L∂z(l+1)\frac{\partial L}{\partial z^{(l+1)}}∂z(l+1)∂L分配给当前层
- 误差调制:乘以激活函数的导数,控制误差的流通量
这实际上是一个与旋转180度的卷积核进行的卷积操作,确保误差按照前向传播的贡献比例进行分配。
2.2 卷积核梯度的计算
卷积核参数的梯度由以下公式给出:
∂L∂gij(l)=∑y=0H∑x=0W∂L∂zyx(l+1)a(y−i)(x−j)(l)\frac{\partial L}{\partial g_{ij}^{(l)}} = \sum_{y=0}^{H} \sum_{x=0}^{W} \frac{\partial L}{\partial z_{yx}^{(l+1)}} a_{(y-i)(x-j)}^{(l)}∂gij(l)∂L=y=0∑Hx=0∑W∂zyx(l+1)∂La(y−i)(x−j)(l)
这个公式的物理意义十分深刻:它等于第l层输入特征图a(l)a^{(l)}a(l)与第l+1层误差信号∂L∂z(l+1)\frac{\partial L}{\partial z^{(l+1)}}∂z(l+1)∂L的互相关操作。
三、视觉化理解:滑动窗口的梯度计算
幻灯片中的图示清晰地展示了这一过程:
- 滑动窗口操作:误差图在输入特征图上滑动,在每个位置执行逐元素乘法
- 局部求和:将窗口内的乘积结果求和,得到卷积核一个位置的梯度值
- 遍历完整图 :重复此过程,重构出整个卷积核的梯度∂L∂g(l)\frac{\partial L}{\partial g^{(l)}}∂g(l)∂L
这个过程可以理解为:寻找输入特征图中哪些模式与较大的误差相关联。如果某个模式频繁出现在高误差区域,相应的卷积核权重就会获得较大的梯度更新。
四、训练流程:从理论到实践
完整的训练迭代包含以下步骤:
- 前向传播:输入批次数据,计算各层输出和最终损失
- 反向传播 :
- 计算输出层梯度
- 递归应用链式法则,逐层传播误差信号
- 计算各层卷积核的梯度
- 梯度平均:对批次内所有样本的梯度求平均,提高稳定性
- 参数更新 :使用梯度下降更新卷积核参数:gnew(l)=gold(l)−η∂L∂g(l)g^{(l)}{new} = g^{(l)}{old} - \eta \frac{\partial L}{\partial g^{(l)}}gnew(l)=gold(l)−η∂g(l)∂L
五、物理直觉:网络在学习什么?
通过分析这些公式,我们可以建立对CNN学习的直观理解:
- ∂L∂z(l)\frac{\partial L}{\partial z^{(l)}}∂z(l)∂L的传播实现了"责任分配",确定每层神经元对最终误差的贡献程度
- ∂L∂g(l)\frac{\partial L}{\partial g^{(l)}}∂g(l)∂L的计算实现了"模式识别",找出输入中与误差减少最相关的视觉特征
卷积核实际上学习的是:为了最小化损失,应该对输入中的何种模式保持敏感。例如,在数字识别任务中,针对数字"1"的过滤器会逐渐学会对垂直线条产生强烈激活。
六、结论
卷积神经网络中的反向传播是一个精妙的数学过程,它通过链式法则和卷积操作的特有性质,将最终损失的责任公平地分配给网络中的每个参数。这种机制使得CNN能够从原始像素中自动学习层次化的特征表示,无需人工设计特征,这是深度学习在计算机视觉领域取得突破的关键所在。