1.论文链接:Graphical Models and Multivariate Analysis of Microarray Data

摘要:
基因表达数据的通常分析忽略了基因表达值之间的相关性。从生物学上讲,这种假设是不合理的。本章介绍的方法允许通过稀疏高斯图形模型来描述基因之间的相关性:稀疏逆协方差矩阵及其相关图形表示用于捕获基因网络的概念。现有的方法及其在识别这种逆协方差矩阵中的零模式所引起的问题中的局限性。本章提供了一个确定零点模式的可行解决方案。本章的另外两个重要贡献是一种非常高维的建模方法和一种假设检验的无分布方法。这些测试解决了对疾病表达和疾病联系的评估,这是本章介绍的一个新概念。给出了一个处理真实的数据的例子。
**关键词:**基因网络,微阵列,高斯图模型,逆协方差矩阵,稀疏矩阵
基因表达数据的通常分析忽略了基因表达值之间的相关性。从生物学上讲,这种假设是不合理的。本章介绍的方法允许通过稀疏高斯图形模型来描述基因之间的相关性:稀疏逆协方差矩阵及其相关图形表示用于捕获基因网络的概念。现有的方法及其在识别这种逆协方差矩阵中的零模式所引起的问题中的局限性。本章提供了一个确定零点模式的可行解决方案。本章的另外两个重要贡献是非常高维建模的方法和假设检验的无分布方法。这些测试解决了对疾病表达和疾病联系的评估,这是本章介绍的一个新概念。给出了一个处理真实的数据的例子。
3.1介绍
一个典型的基因表达数据集由一组受试者的大量基因的测量值组成,这些受试者已经接受了预先指定的艾德治疗或具有已知的基因型。这些数据被排列成一个n × p矩阵,其中n(样本大小)通常为数十到数百的数量级,p为数万或更多的数量级。一个简单而常见的治疗结构是每个个体要么接受治疗(治疗),要么不接受治疗(对照)。对这些数据的通常分析[21]试图鉴定不同表达的基因,即,治疗组的平均表达显著高于或低于对照组的平均表达的基因。通常的分析不试图对基因之间的相关结构进行建模,因此有效地假设基因表达测量是不相关的。从生物学上讲,这种假设是不合理的,因为基因是通过通路或网络连接起来的。
在这一章中,我们提出了一个模型,基因表达数据,明确允许基因之间的相关性。然而,在试图为基因表达数据集的相关性或协方差矩阵建模时,我们遇到了几个需要克服的问题。首先,由于样本大小n相对于变量(基因)的数量p较小,样本协方差矩阵是奇异的(不是满秩或可逆的),即,变量比样本多。这引起了关于估计协方差矩阵(或等价地其逆矩阵)的能力和估计的质量的问题,因为通常的理论假设样本比变量多得多。其次,协方差矩阵或相关矩阵中的条目或参数的数量是天文数字,数亿的数量级是很常见的。显然,我们必须以某种方式减少这些参数的数量,以便取得进展。
可以在这种情况下使用的一类有吸引力的模型是高斯图形模型[14,22],它由逆协方差矩阵中的零模式定义。将这些模型应用于基因组数据已经变得流行,参见例如[20,5]和其中的参考文献。乍一看,考虑逆协方差矩阵似乎不太寻常,但如下所示,它是一个有趣的对象,因为它编码了每个基因和其余基因之间的所有回归关系。此外,逆协方差矩阵中的零指定基因之间的条件独立约束[14,22]。高斯图形模型有效地解决了上述问题,只要它们是稀疏的,即,它们具有大量的等于零的逆协方差矩阵的0对角元素。这些模型也可以方便地用图形表示,当应用于基因表达数据时,提供了一个基因网络的表示,作为分析的背景,包括基因表达,可以发生。生物网络的稀疏性的论证可以在[15]中找到。
这项工作与现有的基因表达数据图形模型的工作不同,因为它不仅试图识别基因网络,而且还分析了网络背景下的治疗效果。其他新的元素是一个非常高维的建模算法和一个假设检验的无分布方法。下面的讨论是[12]的稍微简化的艾德版本,但是增加了对基因之间所有关系的信噪比的计算,以及从多变量角度识别感兴趣基因的替代分析策略。在这个框架中,不被不同地表达或不同地连接的基因(见下文)仍然可能看起来很有趣。
本章的结构如下。第3.2节给出了数据指定的均值和协方差模型艾德。在3.3节中,我们讨论了模型中均值和协方差逆参数的极大似然估计的计算,包括确定协方差逆矩阵中的零点模式。假设检验在第3.4节中介绍,我们考虑对治疗组和对照组之间无差异的假设进行总体检验,以及对组分差异的检验。我们还考虑对多个测试进行调整。在3.5节中给出了一个例子来说明本章提出的思想,我们在3.6节中进行了讨论。
3.2模型




例如,从这个图中我们可以看到,变量/顶点5的邻居是2和3,变量5对其余变量的回归只有变量2和3的非零回归系数。更详细的信息可以在[14]和[22]中找到。关于分布假设,对于图3.1,我们有一个多维多元正态分布,因此每个节点/顶点都有一个单变量高斯分布。

3.3模型拟合

3.3.1零模式已知时的最大似然估计




3.3.2确定逆协方差矩阵中的零点模式
显然,在给定数据矩阵X的情况下,识别逆协方差矩阵中的零模式是一个重要的基本问题,其解决方案有效地确定了基因表达值之间的相互关系。请注意,确定零的模式等价于确定非零的模式的问题,我们通过确定下面的非零模式来解决这个问题。
给定回归系数和逆协方差矩阵元素之间的关系式(3.4),以下直观吸引人的方法表明了自己:



3.4假设检验


3.4.1按排列的随机分布
由于我们已经估计了逆协方差矩阵,并且可能在零模式中存在误差,而不是假设多元正态性,因此我们将使用排列来获得参数估计值的零分布及其各种函数。在[7]之后,我们使用下面的策略。

3.4.2多元检验统计量

3.4.3检验统计量的划分





3.4.4测试策略
在前面的小节中,我们介绍了一些检验统计量和用于显著性检验的相关零分布的计算。我们现在提出两种不同的策略,用于将上述信息组织到数据集的分析中。

在计算零分布时,需要选择排列的数量m,以便至少有几个排列的统计值大于所选的分位数。
注意,上面描述的零分布是无分布的,因为它们只依赖于一阶和二阶矩,而不依赖于高斯假设。与其他方法(如t检验)不同,不需要为每个单独的测试估计或正则化除数。因此,我们不依赖于模型假设来提供方差和检验的正则化估计。与通常的基于模型的方法相比,测试结果会有一些差异(特别是在小样本量的情况下),这并不奇怪。
3.5例子
为了说明上面提出的一些想法,我们使用[23]中的数据。这些数据包括使用AYENU133A芯片获得的29个基因表达测量样本。这里的"治疗组"由来自患有乳腺癌的女性的14个明显正常的乳腺上皮细胞样品组成,并且对照组由来自正在进行乳房缩小手术的没有乳腺癌的女性的15个明显正常的乳腺上皮细胞样品组成。该研究试图确定乳腺癌患者正常上皮细胞的异常,这可能会改善癌症风险评估。在[23]之后,我们删除了两组之间变异很小的基因,这导致研究中剩余14681个基因。
由于样本量小,为了确定逆协方差矩阵中的零模式,我们将每个基因的邻居搜索限制为最多两个基因,对应于每个回归系数大约15个观测值。请注意,这并不意味着一个基因的最大连接数是2,如下所示。显然,我们不能指望可靠地对这个数据集建立一个全面的网络结构,但我们可以希望估计它的一些强连接(子)分量。应用第3.3.2小节中描述的零模式检测策略,我们得到了一个具有24313个非零元素的稀疏逆协方差矩阵。该模型的图相对简单,具有3395个大小为1的团,即,明显独立的基因,和9632个大小为2的集团。这意味着模型的图是一个简单的树状结构。回归关系(3.5)的信噪比的中位数约为1.5。
我们可以像在[12]中那样产生不同表达和不同连接的基因列表。然而,为了说明一些不同的东西,我们将使用整体测试(3.14)的组件来识别网络中有趣的基因和有趣的地方。这对应于使用第3.4.4小节中提到的第二种测试策略。
为了测试,我们使用m=40 000个排列来生成空分布。显著性水平是由先验保守地确定的,假设多达一半的基因可以被不同地表达,多达一半的基因可以被不同地连接,所以我们可能期望做大约2p检验。换句话说,为了确定T的显著成分,我们做p检验,然后确定所选基因的差异表达和连接,我们最多做一个额外的p检验。假阳性的预期数量设定为14.681,给出用于多重检验的p值为5 × 10的-4次方。
两组平均基因表达相同的假设的总体检验得到的T统计值为5771.52,p值严格小于2.5 × 10的-5次方。因此,有强有力的证据表明这两个群体之间的表达差异。图3.2给出了该检验的零分布图。垂直线位于T = 2744.16处,这是对应于p值0.05的分位数。

图3.3说明了T统计量的显著分量的检验。在图3.3中,T的分量和为多重检验调整的显著性水平已经被转换,使得上临界水平和下临界水平分别为1和-1。实际上,-1处的下边缘比图中显示的要粗糙得多。然而,大量的基因在x轴相对较小的空间中绘制掩盖了这一事实。

共有167个成分被艾德为重要成分。与其中一些基因相关的有趣功能是免疫反应、细胞内信号传导、细胞形态发生、细胞周期调节和蛋白质水解。该列表还包含已知与乳腺癌或乳腺癌易感性相关的基因。T的最大组分对应于基因BTG2,其在[23]中被置于转录因子和调节因子的类别中。我们提取了这个基因的邻居,如图3.4所示。该关系的估计信噪比为4.74。对这些基因的粗略功能分析[9,10]揭示了描述性词语,如"细胞凋亡抑制"、"B细胞存活途径"和已知在肿瘤中缺失的蛋白质产物。这说明了图3.4中的基因和关系。在生物学上是有趣的,值得进一步研究。

进一步测试,在167个具有显著T成分的基因中,47个是差异表达的,136个是差异连接的。有41个基因既有差异表达又有连接,有趣的是,有25个既没有显著差异表达也没有连接,这表明有可能发现既没有差异表达也没有差异连接的感兴趣的基因。
我们还建立了一个规模为3的本地网络(即,从一个特定的艾德基因到任何其他相连基因的最多三条边)。图3.5给出了其中具有最多边的局部网络。RPS11基因回归的估计信噪比为21.2,表明存在非常强的关系。有趣的是,注意到与KEGG途径"核糖体"相关的基因的过度表达(例如,以RP开头的名称)。显然,我们有肥沃的土壤来更详细地检查167个基因及其关系,已知的途径,以及与乳腺癌的发展和检测有关的功能。这些列表还可能包含尚未记录的新功能和途径。

图3.5中的基因似乎都没有差异表达。通常,我们可能期望通过涉及基因及其邻居的差异表达模式来解释差异连接。在这里,情况似乎并非如此,例如,我们可以假设转录后调节的可能性。在任何情况下,为了进一步探索这一点,我们在图3.6中绘制了基因RPS 11与其紧邻基因的表达模式。在图中,黑线标识了每个基因的观察对比值。箱形图与对比值的零分布相关,并为每个基因绘制了四分位数间距和临界分位数。在须线极值之间的值不被认为是不同的表达。将RPS 11的对比度的预期值作为其相邻对比度的加权和绘制为灰点。估计的回归系数,除了RPS 11的值,它是估计的残差方差,也显示在图上。
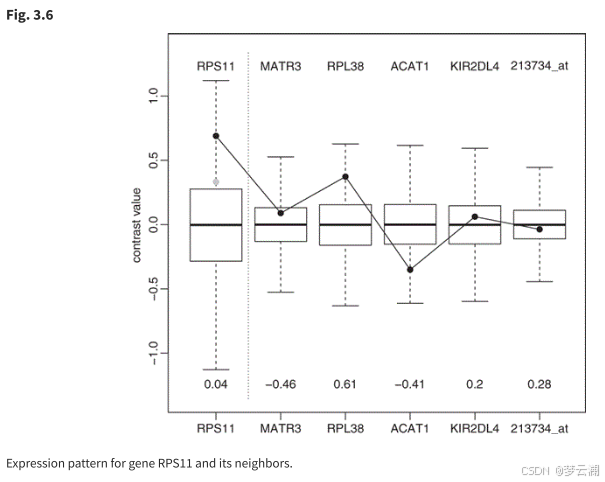
基于该图,灰点的位置似乎主要是由于基因RPL 38和ACAT 1的对比度值。与RPS 11对比值的差异令人感兴趣,需要进一步研究。我们也可以为另一个不同连接的基因MATR3绘制类似的图。
3.6讨论和结论
在本章中,我们提出了一个微阵列数据模型,它特别允许基因之间的相关性。我们展示了如何估计模型中的平均参数以及逆协方差矩阵中的参数,包括其零模式。这涉及确定每个基因和其余基因之间的回归关系,这是一个在通常的基因表达分析中不进行的计算要求很高的步骤。我们还介绍了涉及基因及其近邻的差异连接的概念。给定参数估计值,我们通过使用排列构造了假设的无分布检验。这些测试对于微分表达式的分析也很有用。我们得出了一个整体的假设检验,以及对单个组件的测试,并对多个测试进行了调整。会上展示了如何以图形方式表示模型,以及如何在模型图(网络)的范围内进行数据分析。在这个例子中,我们展示了一种分析数据的替代方法,它超越了产生不同表达基因的列表,并尊重基因可以属于生物途径的想法。
如果我们考虑逆协方差矩阵中的每个非零条目可能是确定两个基因之间关系的生物学原因的实验的基础的可能性,那么很明显,在微阵列数据集中存在压倒性的信息量的潜力,并且这些信息通常被忽视。图形是总结此信息的一种方便方法,但还需要做更多工作才能操作和显示这些非常大的稀疏图形。
现在我们来讨论一些新的想法和上述工作的扩展。有趣的是,考虑数据转换的可能性,试图使数据看起来更多元正态,因为这可能会改善基因之间的线性预测关系(例如,参见[17])。图形查询,如两个基因之间的最短路径,局部连接,枚举基因的集团,并确定基因的连接组件很容易做到,也可以提供有用的信息。
任何一个基因和它的邻居之间的回归关系都可以通过交叉验证、模型检验和检验设定值和残差进行进一步的统计分析。检查线性假设也很有趣。在生物学水平上,我们可以在文献中搜索已知的关系,这可能有助于解释回归结果。然而,我们应该对发现新关系的可能性保持开放,因为现有的知识是不完整的。
在本章中,我们假设治疗组和对照组具有相同的逆协方差矩阵;然而,也可以建立和检验允许治疗组和对照组具有不同逆协方差矩阵的模型。这样的模型将允许治疗激活不同的生物途径或以不同方式激活相同途径的可能性。为了可行,这将要求每个组都有相当多的观察结果。
我们在本章中使用了无向图模型;然而,给定变量的顺序,我们也可以使用有向图模型(贝叶斯网络(BN))来建模协方差矩阵。在这种情况下,逆协方差矩阵的稀疏Cholesky因子成为感兴趣的对象,因为它编码每个变量与其前任或父变量之间的回归关系。在这种情况下,也可以进行类似于上面的分析。
本章中的结果是使用R包sparse. inv.cov和mvama生成的。这些软件包沿着有一些简单的教程,可以从以下网址免费获得:http://www.bioinformatics.csiro.au.
总之,微阵列数据集中的信息比通常的分析提取物多得多。在本章中,我们提出了一些提取这些附加信息的策略,并展示了图形模型在表示这些信息和指导分析方面的有用性。
参考文献
略