树和图论
树的遍历模版
c++
#include <iostream>
#include <cstring>
#include <vector>
#include <queue> // 添加queue头文件
using namespace std;
const int MAXN = 100; // 假设一个足够大的数组大小
int ls[MAXN], rs[MAXN]; // 定义左右子树数组
//后序遍历
void dfs(int x) {
if(ls[x]) dfs(ls[x]);
if(rs[x]) dfs(rs[x]);
cout << x << ' ';
}
//层序遍历
void bfs() {
queue<int> q;
//起始节点入队
q.push(1);
//队列不为空则循环
while(q.size()) {
//访问队列元素x
int x = q.front();
//取出队列元素
q.pop();
//一系列操作
cout << x << " ";
if(ls[x]) q.push(ls[x]);
if(rs[x]) q.push(rs[x]);
}
}
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> ls[i] >> rs[i];
}
dfs(1);
cout << endl;
bfs();
return 0;
}最近公共祖先LCA
本质是一个dp,类似于之前的ST表
fa[i][j]表示i号节点,向上走2^j所到的节点,当dep[i]-2^j>=1时fa[i][j]有效
又因为我们知道2^(j-1) + 2^(j-1)= 2^j, i的2^(j-1) 级祖先的2^(j-1)级祖先 就是i的2^j级祖先。
形象理解:
我们要求x(5号节点)与y(10号节点)的 LCA
倍增的时候,我们发现y的深度比x的深度要小,于是现将y跳到8号节点,使他们深度一样:

这个时候,x和y的深度就相同了,于是我们按倍增的方法一起去找LCA
我们知道n(10)之内最大的二的次方是8,于是我们向上跳8个单位,发现跳过了。
于是我们将8/2变成4,还是跳过了。
再将4/2变成2,跳到了0号节点。
虽然这时跳到了LCA,但是如果直接if(x==y)就确定的话,程序无法判断是刚好跳到了还是跳过了,应为跳过了x也等于y
于是我们需要刚好跳到LCA的儿子上,然后判断if(x的爸爸==y的爸爸)来确定LCA
由于每一个数都可以分解为几个2^n的和(不信自己试),所以他们一定会跳到LCA的儿子上
于是我们就找到了LCA啦!
代码模版:
c++
int lca(int x,int y){
//x喜欢跳。。。
//如果x深度比y小,交换x和y 保证x深度大
if(dep[x]<dep[y]) swap(x,y);
//贪心:i从大到小
//x向上跳的过程中,保持dep[x]>=dep[y],深度不能超过y
for(int i=20;i>=0;i--){
if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
}
//x跳完 此刻x和y的dep相同
//如果发现相遇了 那么就是这个点
if(x==y) return x;
//(int)(log(n)/log(2))就是n以内最大的2的次方,从最大的开始倍增
for(int i=(int)(log(n)/log(2));i>=0;i--)
//如果x和y爸爸不想同 则没有找到
//整个跳跃过程中,保持x!=y,不用x=y判断
if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];//x和y一起向上跳
return fa[x][0];//返回他们的爸爸,即是LCA
}可是在写LCA之前,我们还得进行预要处理些什么呢?
1.每一个点的深度,以便到时候判断
2.每一个点2^i级的祖先,以便到时候倍增跳
于是我们用一个dep数组来记录每一个点的深度,再用一个fa[i][j]表示节点i的2^j级祖先
c++
void dfs(int x,int p){
dep[x]=dep[p]+1;//x的深度是他父亲的深度+1
fa[x][0]=p;//2^0是1,x向上一个的祖先就是他爸爸
for(int i=1;i<=20;i++) fa[x][i]=fa[fa[x][i-1]][i-1];//父节点再向上2^i-1
for(const auto &y : g[x]){ //枚举x所有儿子
if(y==p) continue;
//如果不是他爸爸 继续dfs
dfs(y,x);
}
}树的重心
指对于某个点,将其删除后,可以是的剩余联通块的最大值最小的点(剩余的若干子树的大小最小)
性质:
- 中心若干棵子树大小一定**<=n/2**;除了重心以外的所有其他节点,都必然存在一棵节点个数>n/2的子树
- 一棵树至多两个重心,如果存在,则必然相邻;将连接两个重心的边删除后,一定划分为两棵大小相等的树
- 树中所有点到某个点的距离和中,到重心的距离和是最小的
- 两棵树通过一条边相连,重心一定在较大的一棵树一侧的连接点与原重心之间的简单路径上。两棵树大小相同,则重心就是两个连接点。
如何求解重心?
跑一遍dfs,如果mss[x]<=n/2,则x是重心,反之不是。
c++
void dfs(int x,int fa){
//初始化mss/sz数组
sz[x]=1,mss[x]=0;
for(const auto& y:g[x]){
if(y==fa) continue;
dfs(y,x);
sz[x]+=sz[y];
mss[x]=max(mss[x],sz[y]);
}
//后序位置比较mss大小并判断
mss[x]=max(mss[x],n-sz[x]);
if(mss[x]<=n/2) v.push_back(x);
}树的直径
树上任意两节点之间最长的简单路径即为树的「直径」。
直径由u,v决定,若有一条直径(u,v)满足 : **1)**u和v度数均为1;2)在任意一个点为根的树上,u和v中必然存在一个点作为最深的叶子节点。
如何求解直径?
跑两遍dfs:以任意节点为根的树上跑一次dfs求所有点的深度,选最大的点作为u,再以u为根拍一次dfs,最深的点为v,路径上点的个数为树的dep[v]+1(根节点深度为0)/ dep[v](根节点深度为1)
树上差分
差分的思想方法:
如果有一个区间内的权值发生相同的改变的时候,我们可以采用差分的思想方法,而差分的思想方法在于不直接改变区间内的值 ,而是改变区间[ L , r ] 对于 区间 [ 0, L - 1 ] & 区间[ r + 1, R]的 相对大小关系
差分,可以当做前缀和的逆运算。既然是逆运算,运算方法自然就是相反的了。定义差分数组
d i f f i = a i − a i − 1 diff_i=a_i-a_{i-1} diffi=ai−ai−1
compare:
| 原数列 | 9 | 4 | 7 | 5 | 9 |
|---|---|---|---|---|---|
| 前缀和 | 9 | 13 | 20 | 25 | 34 |
| 差分数组 | 9 | -5 | 3 | -2 | 4 |
| 前缀和的差分数组 | 9 | 4 | 7 | 5 | 9 |
| 查分数组的前缀和 | 9 | 4 | 7 | 5 | 9 |
树上差分,就是利用差分的性质,对路径上的重要节点进行修改(而不是暴力全改),作为其差分数组的值,最后在求值时,利用dfs遍历求出差分数组的前缀和,就可以达到降低复杂度的目的。
这里差分的优点就非常明显了:
- 算法复杂度超低
- 适用于一切 连续的 "线段"
这里所谓的线段可以是一段连续的区间,也可以是路径
点差分:
模版题目:给出一棵 n 个点的树,每个点点权初始为 0,现在有 m 次修改,每次修改给出 x,y,将 x,y 简单路径上的所有点的点权 +d,问修改完之后每个点的点权。
将序列差分转移到树上:比如我们要对 x,y 的路径上的点统一加上 d。
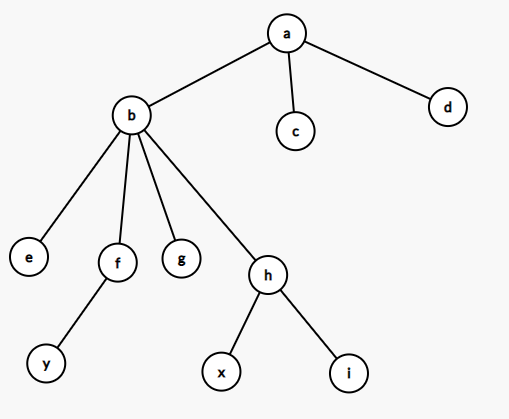
涉及到的点有:x,h,b,f,y因此对于点 a 我们不能有影响,操作方案就是 b(回溯时左右加了两次)的点权减去 d,a 的点权减去 d。
最后我们对整棵树做一遍 dfs,将所有点的点权 变为其子树(含自己)内所有点的点权,这个操作仿照求每个点子树的 Size 就可以完成了。
模版代码:
同样需要lca的两个模版函数,并添加:
dlt[i]:存放每个点经过的次数
c++
void dfs1(int x){
for(int i=0;i<v[x].size();i++){
int u=v[x][i];
if(u!=fa[x][0]){
dfs1(u);
//回溯
dlt[x]+=dlt[u];
}
}
return;
}
int main() {
cin>>n>>k;
maxx=log2(n);
for(int i=1;i<n;i++){
int a,b;cin>>a>>b;
v[a].push_back(b),v[b].push_back(a);
}
dfs(1,0);
//k次询问 处理k条路径
for(int i=1;i<=k;i++){
int a,b;cin>>a>>b;
dlt[a]++,dlt[b]++;
int c=lca(a,b);
dlt[c]--,dlt[fa[c][0]]--;
}
dfs1(1);
for(int i=1;i<=n;i++) cout<<dlt[i]<<" ";
return 0;
}美妙的例题:
P3258 [JLOI2014\] 松鼠的新家 - 洛谷 (luogu.com.cn)](https://www.luogu.com.cn/problem/P3258)
###### 边差分:
模版题目:给出一棵 n个点的树,每条边边权初始为 0,现在有 m 次修改,每次修改给出 x,y将 x,y简单路径上的所有**边**边权 +d,问修改完之后每条边的边权。
首先我们需要一种叫做\*\*"边权转点权"**的方法,就是对于每个点我们认为其点权代表**这个点与其父节点之间的边的边权\*\*,对于每条边我们认为其边权是这条边所连两个点中深度较大的点的点权,根节点点权无意义。
还是修改 x,y路径上的边,还是这张图:

涉及的边/点:`x,h,f,y`,对于点 `b` 我们不能有影响,操作方案就是 b(回溯时左右加了两次 实则不变)的点权(b与父亲节点的边权)减去 2d。
同样的做完之后一遍 dfs 求一下每个点的点权即可。
##### 图的遍历模版
###### DFS:
```c++
bitset