希尔排序：Python语言实现

希尔排序也称"递减增量排序"，它对插入排序做了改进，将列表分成数个子列表，并对每一个子列表应用插入排序。如何切分列表是希尔排序的关键------并不是连续切分，而是使用增量 i（有时称作步长）选取所有间隔为 i 的元素组成子列表。

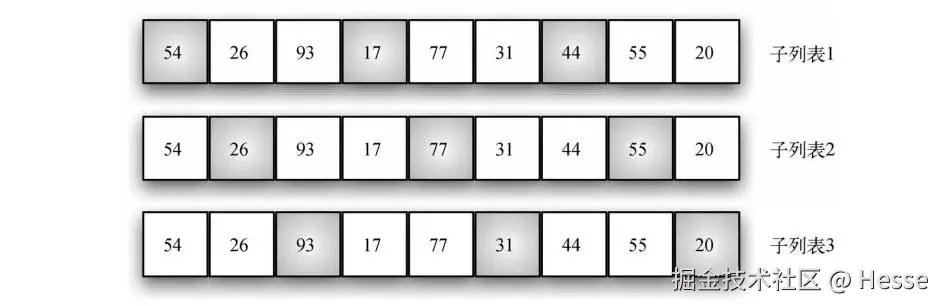
以下图中的列表为例，这个列表有 9 个元素。如果增量为 3，就有 3 个子列表，每个都可以应用插入排序，结果如后面的图所示。尽管列表仍然不算完全有序，但通过给子列表排序，我们已经让元素离它们的最终位置更近了。

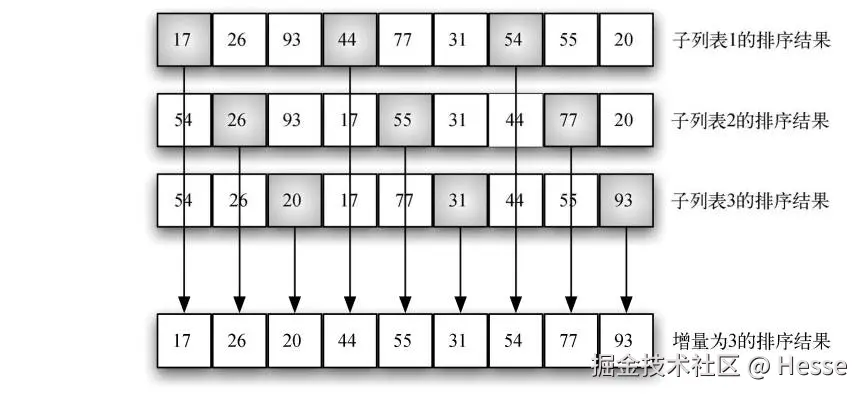
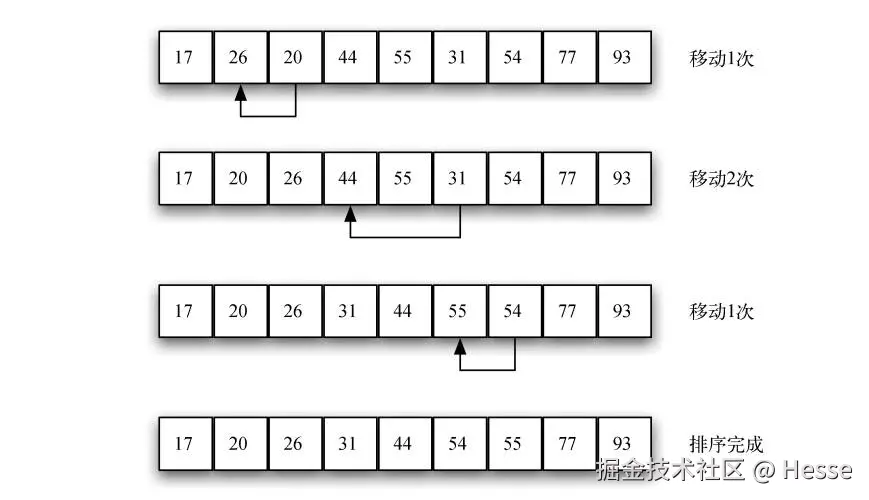
下展示了最终的插入排序过程。由于有了之前的子列表排序，因此总移动次数已经减少了。本例只需要再移动 4 次。

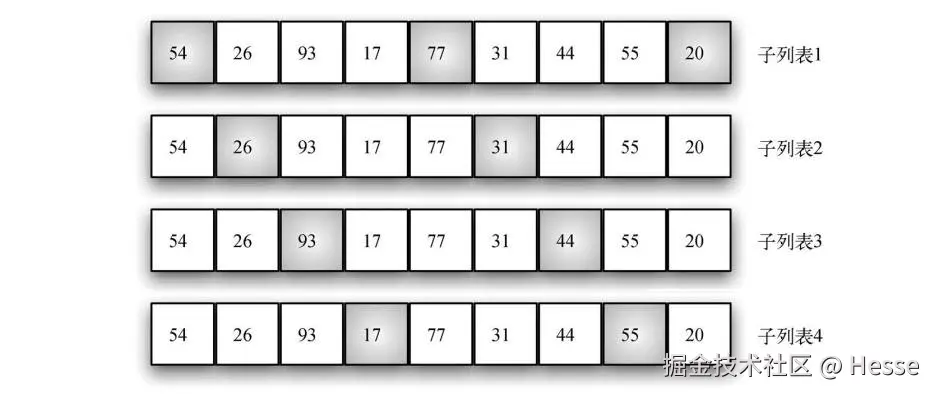
如前所述，如何切分列表是希尔排序的关键。后面的代码实现中的函数采用了另一组增量。先为 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 \frac{n}{2} </math>2n个子列表排序，接着是 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 4 \frac{n}{4} </math>4n 个子列表。最终，整个列表由基本的插入排序算法排好序。下图展示了采用这种增量后的第一批子列表。

python 复制代码

def shell_sort(alist):
    sublistcount = len(alist) // 2
    while sublistcount > 0:
        for startposition in range(sublistcount):
            gap_insertion_sort(alist, startposition, sublistcount)

        sublistcount = sublistcount // 2

def gap_insertion_sort(alist, start, gap): 
    for i in range(start+gap, len(alist), gap):
        currentvalue = alist[i]
        position = i

        while position >= gap and alist[position-gap] > currentvalue:
            alist[position] = alist[position-gap]
            position = position-gap

        alist[position] = currentvalue

测试代码：

python 复制代码

a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20]
print(f"before sorting: {a_list}")
shell_sort(a_list)
print(f"after sorting: {a_list}")
assert a_list == sorted(a_list)

输出：

ini 复制代码

before sorting: [54, 26, 93, 17, 77, 31, 44, 55, 20]
after sorting: [17, 20, 26, 31, 44, 54, 55, 77, 93]

性能测试：

python 复制代码

%timeit shell_sort(a_list)

结果：

sql 复制代码

1.43 μs ± 3.01 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)

希尔排序的时间复杂度大概介于 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ) O(n) </math>O(n) 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2) 之间。若采用上面代码中的增量，则时间复杂度是 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 2 ) O(n^2) </math>O(n2) 。通过改变增量，比如采用 <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 k − 1 ( 1 , 3 , 7 , 15 , 31 , ⋯ ) 2^k-1 (1, 3, 7, 15, 31, \cdots) </math>2k−1(1,3,7,15,31,⋯)，希尔排序的时间复杂度可以达到 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 3 2 ) O(n^{\frac{3}{2}}) </math>O(n23)。

参考文档

《Python数据结构与算法分析（第2版）》：5.3.4 希尔排序