效果预览

fig.1 demo 演示效果
前几天在 openprocessing 闲逛时,偶然发现了一个特别吸引我的动画效果------闭合的平滑曲线如同水波般优雅地流动变换,无独有偶,在一款白噪音助眠应用"潮汐"的界面中也看到过极为相似的设计语言,流畅的曲线随着声音节奏轻轻起伏,营造出令人放松的视觉效果。
最让我惊讶的是,这个即简约又充满韵律感的动画效果,核心代码竟然只有短短几行
scss
function setup() {
createCanvas(windowWidth, windowHeight);
}
function draw() {
blendMode(BLEND);
background(245);
blendMode(MULTIPLY);
noStroke();
translate(width/2,height/2);
fill(255,150,0);
drawLiq(8,100,80,200);
}
function drawLiq(vNnum,nm,sm,fcm){
push();
rotate(frameCount/fcm);
let dr = TWO_PI/vNnum;
beginShape();
for(let i = 0; i < vNnum + 3; i++){
let ind = i%vNnum;
let rad = dr *ind;
let r = height*0.3 + noise(frameCount/nm + ind) * height*0.1 + sin(frameCount/sm + ind)*height*0.05;
curveVertex(cos(rad)*r, sin(rad)*r);
}
endShape();
pop();
}而其中最关键的,是两个函数
- noise(Perlin noise):噪波函数
- curveVertex:Catmull-Rom 样条曲线
出于好奇,我试着去研究它们的实现原理,这个过程让我再次感受到,数学的魅力无处不在。
Perlin Noise
认识 Noise 函数
Perlin Noise(柏林噪声)是由计算机科学家 Ken Perlin 在 1983 年提出的一种梯度噪声算法。它能够生成自然、连续且随机的数值,广泛应用于计算机图形学、游戏开发和模拟自然现象(如地形、云层、火焰等)。与纯粹的随机噪声不同,Perlin Noise 具有平滑过渡的特性,使其更接近真实世界的自然纹理。
Perlin Noise 通过在空间中划分网格,并在每个网格节点上赋予随机梯度向量,然后通过插值计算出任意点的噪声值。这种算法能够在多次调用(相同的输入参数)时保持一致的数值,适合用于需要连续性和一致性的场景。
Perlin Noise 原理
Perlin Noise 的核心思想是通过插值使随机值平滑过渡。其实现步骤大致如下
- 网格定义:将空间划分为规则的网格,每个网格顶点分配一个随机梯度向量(单位向量)。
- 点积计算:对于空间中的任意一点,找到其所在网格的四个顶点,并计算该点到顶点的向量与顶点梯度向量的点积。
- 插值平滑:使用缓和曲线(如五次多项式)对四个顶点的点积结果进行双线性插值,确保噪声平滑过渡。
通过调整频率(网格密度)和叠加多层噪声(分形噪声),可以生成更复杂的自然效果。Perlin Noise 因其计算高效和自然表现,成为程序生成内容的重要工具。
MatheMatica 演示 Perlin Noise 的计算
ini
(* 1. 定义辅助函数 *)
(* 生成随机单位向量 *)
randomUnitVector := Normalize@RandomReal[{-1, 1}, 2]
(* 生成梯度向量网格 *)
generateGradientGrid[size_] := Table[randomUnitVector, {size}, {size}]
(* 平滑插值函数 *)
fade[t_] := 6 t^5 - 15 t^4 + 10 t^3;
(* 线性插值 *)
lerp[a_, b_, t_] := a + t*(b - a)
(* 2. Perlin Noise 核心函数 *)
perlinNoise2D[gradients_, x_, y_] :=
Module[{x0, y0, x1, y1, sx, sy, u, v, a, b},
(* 确定网格单元 *)
x0 = Floor[x];
y0 = Floor[y];
x1 = x0 + 1; y1 = y0 + 1;
(* 计算相对位置 *)
sx = x - x0; sy = y - y0;
(* 计算四个角点的贡献 *)
u = dotProduct[gradients, x0, y0, x, y];
v = dotProduct[gradients, x1, y0, x, y];
a = lerp[u, v, fade[sx]];
u = dotProduct[gradients, x0, y1, x, y];
v = dotProduct[gradients, x1, y1, x, y];
b = lerp[u, v, fade[sx]];
lerp[a, b, fade[sy]]]
(* 点积计算辅助函数 *)
dotProduct[gradients_, ix_, iy_, x_, y_] :=
Module[{gradient, dx, dy}, gradient = gradients[[iy + 1, ix + 1]];
dx = x - ix; dy = y - iy;
gradient . {dx, dy}]
(* 3. 生成噪声图 *)
(* 设置参数 *)
(* 梯度网格大小 *)
gridSize = 3;
(* 噪声分辨率 *)
noiseRes = 0.1;
(* 生成梯度场 *)
gradients = generateGradientGrid[gridSize];
(* 生成噪声数据 *)
noiseData =
Table[perlinNoise2D[gradients, x, y], {y, 0,
gridSize - 1 - noiseRes, noiseRes}, {x, 0,
gridSize - 1 - noiseRes, noiseRes}];
(* 4. 可视化 *)
(* 自定义颜色函数:z 值小->白色,z 值大->蓝色 *)
customColorFunction[z_] := Blend[{{0, White}, {1, Blue}}, z]
(* 基本密度图 *)
plot1 = ListDensityPlot[noiseData,
ColorFunction -> customColorFunction, PlotRange -> All,
ImageSize -> 500, PlotLabel -> "2D Perlin Noise"];
(* 3D表面图 *)
plot2 =
ListPlot3D[noiseData, ColorFunction -> customColorFunction,
PlotRange -> All, ImageSize -> 500, PlotLabel -> "3D Perlin Noise"];
(* 并排显示 *)
Row[{plot1, plot2}]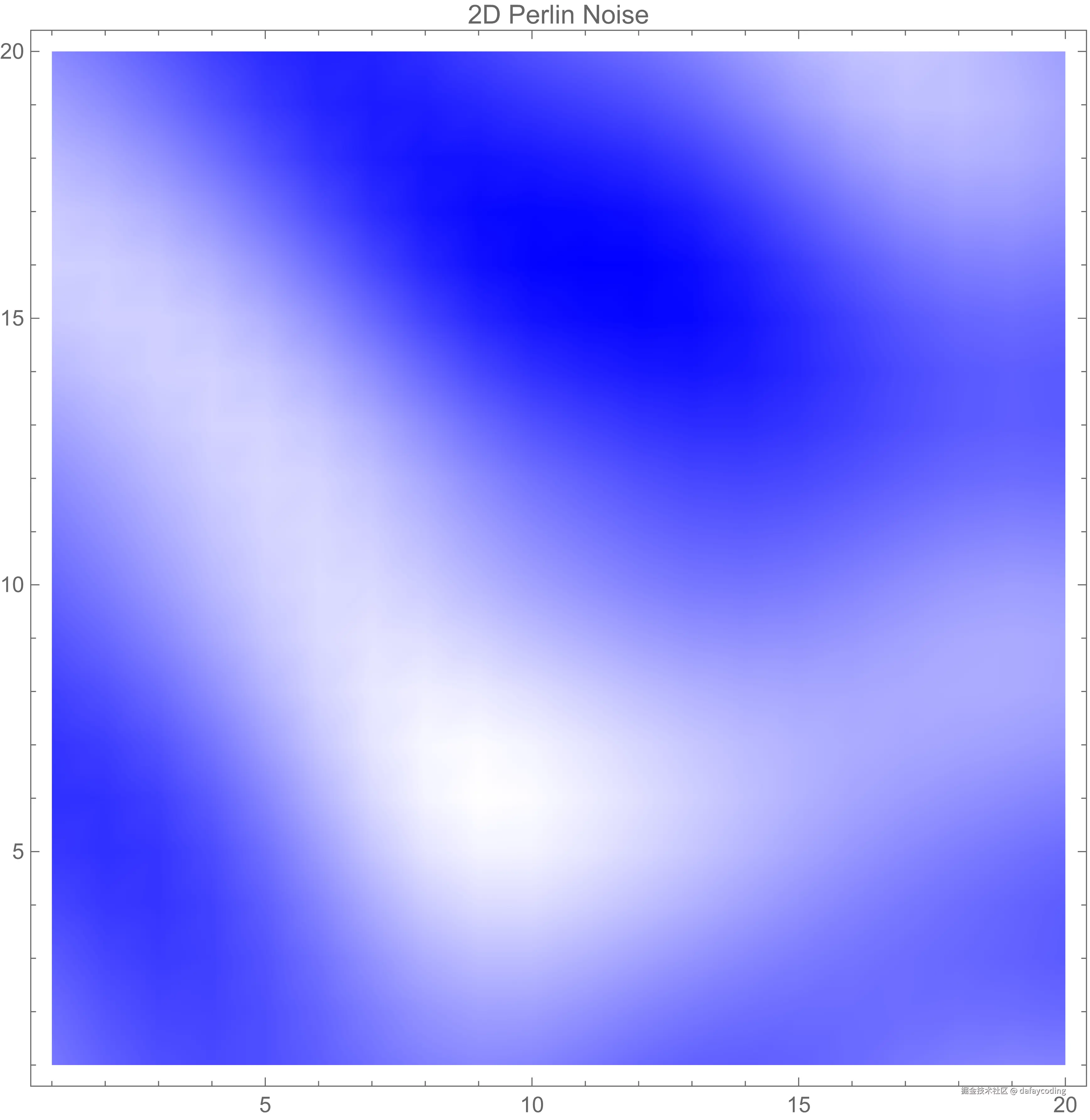
fig.2 2D Perlin Noise

fig.3 3D Perlin Noise
Catmull-Rom
认识 Catmull-Rom 样条曲线
Catmull-Rom 样条曲线是一种插值样条曲线,由 Edwin Catmull 和 Raphael Rom 提出。它能够平滑地穿过给定的控制点,适用于动画路径、相机轨迹和曲线拟合等场景。与 Bézier 曲线不同,Catmull-Rom 曲线保证经过每一个控制点,同时保持局部平滑性,使其在交互式设计中非常实用。
Catmull-Rom 样条曲线原理
Catmull-Rom 曲线的计算基于分段三次插值,其核心步骤如下:
-
局部控制:每四个相邻控制点(Pi−1,Pi,Pi+1,Pi+2)确定一段曲线,仅影响 Pi 到 Pi+1 之间的路径。
-
插值公式:使用 Hermite 插值形式,计算当前点 t∈[0,1] 的位置:
<math xmlns="http://www.w3.org/1998/Math/MathML"> P ( t ) = 0.5 ⋅ ( ( 2 P i ) + ( P i + 1 − P i − 1 ) t + ( 2 P i − 1 − 5 P i + 4 P i + 1 − P i + 2 ) t 2 + ( − P i − 1 + 3 P i − 3 P i + 1 + P i + 2 ) t 3 ) P(t)=0.5⋅((2Pi)+(Pi+1−Pi−1)t+(2Pi−1−5Pi+4Pi+1−Pi+2)t2+(−Pi−1+3Pi−3Pi+1+Pi+2)t3) </math>P(t)=0.5⋅((2Pi)+(Pi+1−Pi−1)t+(2Pi−1−5Pi+4Pi+1−Pi+2)t2+(−Pi−1+3Pi−3Pi+1+Pi+2)t3)
-
张力参数(可选):可通过调整参数控制曲线的"紧度",默认值为 0.5(均匀 Catmull-Rom 曲线)。
Catmull-Rom 曲线无需额外锚点,计算高效,且天然保持 C1 连续性,适合实时应用。
MatheMatica 演示 Catmull-Rom 样条曲线的计算
ini
p0 = {1, 4};
p1 = {3, 5};
p2 = {4, 3};
p3 = {6, 4};
alpha = 0.5; (* 张力参数 *)
t0 = 0;
t1 = EuclideanDistance[p1, p0];
t2 = t1 + EuclideanDistance[p2, p1] ^ alpha;
t3 = t2 + EuclideanDistance[p3, p2] ^ alpha;
CA1[t_] := ((t1 - t)/(t1 - t0)) * p0 + ((t - t0)/(t1 - t0)) * p1;
CA2[t_] := ((t2 - t)/(t2 - t1)) * p1 + ((t - t1)/(t2 - t1)) * p2;
CA3[t_] := ((t3 - t)/(t3 - t2)) * p2 + ((t - t2)/(t3 - t2)) * p3;
CB1[t_] := ((t2 - t)/(t2 - t0)) * CA1[t] + ((t - t0)/(t2 - t0)) *
CA2[t] ;
CB2[t_] := ((t3 - t)/(t3 - t1)) * CA2[t] + ((t - t1)/(t3 - t1)) *
CA3[t] ;
CR[t_] := ((t2 - t)/(t2 - t1)) * CB1[t] + ((t - t1)/(t2 - t1)) *
CB2[t];
Show[
ParametricPlot[
CA1[t], {t, 0, 6},
PlotStyle -> {Thin, Dashing[{0.01, 0.02}], Gray}, (* 红色虚线 *)
PlotRange -> {{-1, 8}, {-1, 8}},
GridLines -> Automatic,
GridLinesStyle -> LightGray,
AxesLabel -> {"X", "Y"}
],
ParametricPlot[
CA2[t], {t, 0, 6},
PlotStyle -> {Thick, Dashing[{0.01, 0.02}], Gray} (* 红色虚线 *)
],
ParametricPlot[
CA3[t], {t, 0, 6},
PlotStyle -> {Thick, Dashing[{0.01, 0.02}], Gray} (* 红色虚线 *)
],
ParametricPlot[
CB1[t], {t, 0, 6},
PlotStyle -> {Thick, Green}
],
ParametricPlot[
CB2[t], {t, 0, 6},
PlotStyle -> {Thick, Green}
],
ParametricPlot[
CR[t], {t, 0, 6},
PlotStyle -> {Thick, Red}
],
Graphics[{
PointSize[0.02], Black, Point /@ {p0, p1, p2, p3},
Black, FontSize -> 12,
Text["p0", p0, {0, 1.5}], Text["p1", p1, {0, 1.5}],
Text["p2", p2, {0, 1.5}], Text["p3", p3, {0, 1.5}]
}]
]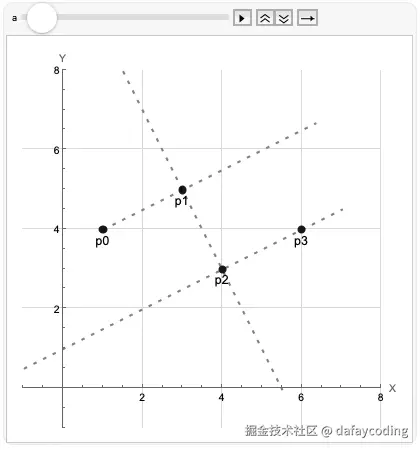
fig.4 Catmull-Rom 计算示例
感兴趣的可以对比下 使用四段三次 Bézier 曲线拟合圆 中的贝塞尔曲线的计算示例图,同样四个点下不同的曲线表现
Android 中的实现
使用 Android 版的 Processing 开源框架
克隆源码 processing (android),主要使用其中的 processing-core 模块, 可在 module 下的 build.gradle 文件中引入
java
implementation project(':libs:processing-core')在 Activity 布局中添加 PFragment
kotlin
class MainActivity : BaseActivity<ActivityMainBinding>(ActivityMainBinding::inflate){
override fun initViews() {
super.initViews()
val sketch = SketchBubble()
val fragment = PFragment(sketch)
fragment.setView(binding.flContent, this)
}
}SketchBubble 中即是具体的动画实现
scss
package com.dafay.demo.lab.noise.processing
import android.graphics.PointF
import com.dafay.demo.lib.base.utils.dp2px
import processing.core.PApplet
class SketchBubble : PApplet() {
private val pointList = mutableListOf<PointF>()
override fun settings() {
size(400.dp2px, 400.dp2px)
}
override fun setup() {
hint(DISABLE_DEPTH_TEST)
background(0f, 255f, 255f)
}
override fun draw() {
// 绘制背景,覆盖上一帧的图像
background(0f, 255f, 255f)
translate(width / 2f, height / 2f)
rotate(frameCount.toFloat() / 500)
drawBubble()
}
/**
* 刷新 point
*/
private fun updatePointList() {
pointList.clear()
val dr = TWO_PI / 8.toFloat()
for (i in 0 until 11) {
val ind = i % 8
val rad = dr * ind
val value1 = height * 0.3
val value2 = noise(frameCount / 500.toFloat() + ind) * height * 0.01
val value3 = sin(frameCount / 80.toFloat() + ind) * height * 0.05
val r = value1 + value2 + value3
val x = cos(rad) * r
var y = sin(rad) * r
pointList.add(PointF(x.toFloat(), y.toFloat()))
}
}
private fun drawBubble() {
stroke(255f, 255f, 125f)
fill(255f, 255f, 0f)
// 刷新点的位置
updatePointList()
beginShape()
pointList.forEach {
// 绘制曲线
curveVertex(it.x, it.y)
}
endShape()
// 绘制点
strokeWeight(PI * 3)
stroke(0f, 0f, 255f)
pointList.forEach {
point(it.x, it.y)
}
}
}-
你可能会遇到的问题
processing (android) 中 curve 相关的绘制有个 bug ------无法清除之前的绘制,调试发现 path 没有进行重置,具体代码如下
ini// PGraphicsAndroid2D.java 文件 public class PGraphicsAndroid2D extends PGraphics { static public boolean useBitmap = true; ... @Override protected void curveVertexSegment(float x1, float y1, float x2, float y2, float x3, float y3, float x4, float y4) { curveCoordX[0] = x1; curveCoordY[0] = y1; curveCoordX[1] = x2; curveCoordY[1] = y2; curveCoordX[2] = x3; curveCoordY[2] = y3; curveCoordX[3] = x4; curveCoordY[3] = y4; curveToBezierMatrix.mult(curveCoordX, curveDrawX); curveToBezierMatrix.mult(curveCoordY, curveDrawY); // since the paths are continuous, // only the first point needs the actual moveto if (vertexCount == 0) { // if (path == null) { // TODO: 这里添加一行代码,对路径进行重置 path.reset(); path.moveTo(curveDrawX[0], curveDrawY[0]); vertexCount = 1; } ... }
- 创意编程还是直接使用 Processing JavaScript 更为高效。相比之下,使用 Android 进行开发不仅繁琐,还受到诸多限制,这让整个过程失去了不少乐趣。
自己动手实现
Android 可以使用自定义 View,覆盖 View::onDraw(),使用 Canvas 进行绘制
kotlin
class BubbleView @JvmOverloads constructor(context: Context, attrs: AttributeSet? = null, defStyleAttr: Int = 0) :
View(context, attrs, defStyleAttr) {
// 画笔
private val paint = Paint().apply {
style = Paint.Style.FILL_AND_STROKE
strokeWidth = 6f
color = Color.YELLOW
isAntiAlias = true
blendMode = BlendMode.SRC_OVER
}
// 噪声生成器
private val noiseGenerator = NoiseGenerator()
// 绘制曲线
private val curveVertexRenderer = CurveVertexRenderer()
private val pointList = mutableListOf<PointF>()
private var frameCount = 0
private val vNum = 8 // 顶点数量
private val nm = 200f // 噪声参数
private val sm = 80f // 正弦参数
private val fcm = 15f // 旋转参数
private val animator = ValueAnimator.ofInt(0, Int.MAX_VALUE).apply {
duration = Int.MAX_VALUE.toLong()
repeatCount = ValueAnimator.INFINITE
addUpdateListener {
frameCount += 1
invalidate()
}
}
override fun onAttachedToWindow() {
super.onAttachedToWindow()
animator.start()
}
override fun onDetachedFromWindow() {
super.onDetachedFromWindow()
animator.cancel()
}
override fun onDraw(canvas: Canvas) {
super.onDraw(canvas)
canvas.translate(width / 2f, height / 2f)
canvas.rotate(frameCount.toFloat() / fcm)
drawBubble(canvas)
}
/**
* 刷新 point
*/
private fun updatePointList() {
pointList.clear()
val dr: Float = ((2 * PI) / vNum.toFloat()).toFloat()
for (i in 0 until vNum + 3) {
val ind: Int = i % vNum
val rad: Float = dr * ind
val value1 = height * 0.3
val value2 = noiseGenerator.noise(frameCount / nm + ind) * height * 0.01f
val value3 = sin(frameCount / sm.toDouble() + ind) * height * 0.03f
val r = (value1 + value2 + value3).toFloat()
val x = cos(rad.toDouble()).toFloat() * r
val y = sin(rad.toDouble()).toFloat() * r
pointList.add(PointF(x, y))
}
}
fun drawBubble(canvas: Canvas) {
updatePointList()
paint.color = Color.YELLOW
curveVertexRenderer.beginShape()
pointList.forEach {
curveVertexRenderer.curveVertex(it.x, it.y)
}
curveVertexRenderer.endShape(canvas, paint)
paint.color = Color.BLUE
pointList.forEach {
canvas.drawCircle(it.x, it.y, 6f, paint)
}
}
/**
* 模拟 noise 函数
* 使用随机数模拟 noise 函数
*/
class NoiseGenerator(private val seed: Int = 0) {
private val permutation = IntArray(512).apply {
val random = Random(seed.toLong())
val p = IntArray(256) { it }
p.shuffle(random)
for (i in 0 until 512) {
this[i] = p[i and 255]
}
}
private fun grad(hash: Int, x: Float): Float {
val h = hash and 15
var grad = 1f + (h and 7) // 梯度值 1-8
if (h and 8 != 0) grad = -grad // 随机一半是负数
return grad * x
}
fun noise(x: Float): Float {
val xi = x.toInt() and 255
val xf = x - x.toInt()
val u = fade(xf)
val a = permutation[xi]
val b = permutation[xi + 1]
return lerp(u, grad(a, xf), grad(b, xf - 1f)) * 0.5f + 0.5f
}
private fun fade(t: Float): Float = t * t * t * (t * (t * 6f - 15f) + 10f)
private fun lerp(amount: Float, a: Float, b: Float) = a + amount * (b - a)
}
/**
* Catmull-Rom 样条曲线绘制
*/
class CurveVertexRenderer {
private val points: MutableList<PointF> = ArrayList()
// p1,p2 之间有多少点,点越多曲线越平滑
private val diff = 0.1f
fun beginShape() {
points.clear()
}
/**
* 收集所有参与绘制的点
*/
fun curveVertex(x: Float, y: Float) {
points.add(PointF(x, y))
}
/**
* 执行绘制
*/
fun endShape(canvas: Canvas, paint: Paint) {
if (points.size < 4) {
return // 至少需要4个点才能生成曲线
}
val path = Path()
for (i in 0..points.size - 4) {
val p0 = points[i]
val p1 = points[i + 1]
val p2 = points[i + 2]
val p3 = points[i + 3]
for (i in 0..(1/diff).toInt()) {
if (i == 0) {
path.lineTo(p1.x, p1.y)
}
val point = catmullRomInterpolation(p0, p1, p2, p3, i*diff)
path.lineTo(point.x, point.y)
}
}
canvas.drawPath(path, paint)
}
/**
* catmull-rom 计算,张力默认 0.5
*/
fun catmullRomInterpolation(
p0: PointF, // 前一个点
p1: PointF, // 起点
p2: PointF, // 终点
p3: PointF, // 后一个点
t: Float // 插值参数 [0,1]
): PointF {
// 计算 x 坐标
val x = 0.5f * (
(2 * p1.x) +
(-p0.x + p2.x) * t +
(2 * p0.x - 5 * p1.x + 4 * p2.x - p3.x) * t * t +
(-p0.x + 3 * p1.x - 3 * p2.x + p3.x) * t * t * t
)
// 计算 y 坐标
val y = 0.5f * (
(2 * p1.y) +
(-p0.y + p2.y) * t +
(2 * p0.y - 5 * p1.y + 4 * p2.y - p3.y) * t * t +
(-p0.y + 3 * p1.y - 3 * p2.y + p3.y) * t * t * t
)
return PointF(x, y)
}
}
}参考文档
原文链接
Smooth Paths Using Catmull-Rom Splines
Bubble circle liquified (openprocessing)
Processing for Android
计算机曲线简史 计算机曲线简史(中文翻译版)
Centripetal Catmull--Rom spline (Wikipedia)
Parameterization of Catmull-Rom Curves(张力示意图)