上一博文学习了小批量梯度下降在神经网络优化中的应用:
在小批量梯度下降法中,批量大小(Batch Size)对网络优化的影响也非常大,本文我们来学习如何选择小批量梯度下降的批量大小。
一、批量大小的选择
一般而言,批量大小不影响随机梯度的期望,但是会影响随机梯度的方差。
批量大小越大,随机梯度的方差越小,引入的噪声也越小,训练也越稳定,因此可以设置较大的学习率。而批量大小较小时,需要设置较小的学习率,否则模型会不收敛。学习率通常要随着批量大小的增大而相应地增大。
一个简单有效的方法是线性缩放规则(Linear Scaling Rule):当批量大小增加 𝑚 倍时,学习率也增加 𝑚 倍。线性缩放规则往往在批量大小比较小时适用,当批量大小非常大时,线性缩放会使得训练不稳定。
我们来分析上面的这段话。
(一)首先,为什么"批量大小越大,随机梯度的方差越小,引入的噪声也越小,训练也越稳定"呢?
下面先给出核心结论:在小批量梯度下降(mini‑batch SGD)中,每次更新所用梯度是对选定批次样本梯度的平均。根据大数定律和方差运算规则,这个平均梯度的方差随着批次大小 B 的增大而减少(具体地,对单个样本梯度方差 σ^2,平均梯度的方差为 σ^2/B),因此批次越大,随机梯度的"噪声"越小,参数更新轨迹越平滑,训练也就越稳定。但批次过大又会降低更新频率、消耗更多内存并可能陷入不理想的平坦区域,所以实际中需在"稳定性"与"效率"之间做权衡。
1. 平均梯度方差随批次大小缩减
-
单样本梯度的随机性
每个训练样本对梯度的贡献视作随机变量,其方差可记作 σ^2。
-
批次梯度为样本梯度的均值
对一个大小为 B 的批次,梯度估计

其方差根据样本独立同分布的假设满足

因此 B 越大,Var(g) 越小,使得每一步的更新更接近于"真实"全量梯度。
2. 数学直观与统计背景
-
大数定律
当 B 足够大时,批次均值近似收敛到总体期望(真实梯度),方差衰减至零。
-
中心极限定理
即便单样本梯度分布非正态,均值在大批次时仍近似正态分布,方差为 σ^2/B。
-
优化平滑性
较小的方差意味着更新方向的随机波动减少,参数更新路径更加平滑,梯度下降的步伐也更稳定,不易在鞍点或小坑中震荡。
3. 稳定性 vs. 更新频率的权衡
-
批次越大
-
噪声小、更新平稳:更接近全量梯度,收敛更规律。
-
计算开销大、更新慢:每次迭代需更多样本,迭代次数减少。
-
-
批次越小
-
噪声大、更新抖动:有助于跳出鞍点,提高泛化。
-
更新快、泛化好:更多次更新让算法能更快"试探"参数空间。
-
(二)上面提到"批量大小较小时,需要设置较小的学习率,否则模型会不收敛。",这是为什么呢?
1. 梯度方差与学习率的关系
1.1 噪声放大与发散风险
一次更新为  。更新的随机波动度量可近似为
。更新的随机波动度量可近似为
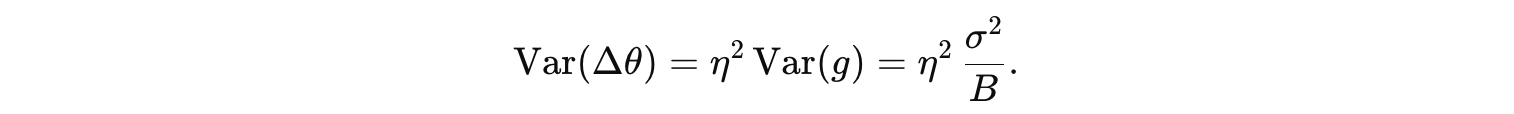
当 B 很小时,若 η不相应减小, 会变得很大,导致更新步长在不同方向上有剧烈抖动,学习过程难以收敛。
会变得很大,导致更新步长在不同方向上有剧烈抖动,学习过程难以收敛。
2. 理论与实证研究
2.1 明确"泛化差距"与鞍点分析
-
Keskar et al. (ICLR 2017) 发现大批量训练易陷入"尖锐最小点"而泛化较差,小批量带来的噪声有助于跳出尖锐谷底,且需适当调低学习率以保持稳定。
-
Masters & Luschi (ICLR 2018) 系统回顾了小批量训练的优势与挑战,指出小批量时梯度噪声大,需要更小的步长以避免震荡和发散。
2.2 动量与超收敛现象
-
Hoffer et al. (arXiv 2017) 演示了在小批量下使用更小学习率并结合动量可以加速训练并稳定收敛。
-
Smith et al. (ICLR 2019) 通过"超收敛"实验,进一步展示学习率和批量大小的精细配合对于噪声平衡和收敛速度的重要性。
3. 实践指南
-
依据批量大小缩放学习率
- 经验法则:当批量大小减小 kkk 倍时,将学习率也减小约 k\sqrt{k}k 至 kkk 倍,以保持更新方差可控。
-
结合动量或自适应优化器
- 在小批量时,动量(Momentum)或 Adam/RMSprop 等优化器可帮助缓冲梯度噪声,提高更新稳定性。
-
监控训练动态
-
观察训练损失曲线平滑度:若出现震荡或不下降,尝试减小学习率;
-
根据验证集性能动态调整,确保既能快速收敛又保持良好泛化。
-
二、回合(Epoch)和迭代(Iteration)的概念
每一次小批量更新为一次迭代,所有训练集的样本更新一遍为一个回合,两者的关系为:

下图说明在 MNIST 数据集上批量大小对损失下降的影响:

从左图可以看出,批量大小越大,下降效果越明显,并且下降曲线越平滑。但从右图可以看出,如果按整个数据集上的回合(Epoch)数来看,则是批量样本数越小,下降效果越明显。适当小的批量会导致更快的收敛。
此外,批量大小和模型的泛化能力也有一定的关系。通过实验发现:批量越大,越有可能收敛到尖锐最小值;批量越小,越有可能收敛到平坦最小值。
三、在神经网络参数优化当中,采用小批量梯度下降,如何确定批量大小呢?
在神经网络训练中,确定小批量梯度下降(Mini-batch Gradient Descent)的批量大小(Batch Size)需要综合考虑计算效率、内存限制、优化效果和泛化性能。
1. 基本原则与经验法则
-
常见初始值 :通常从 32、64、128、256 等 2 的幂次开始(因内存对齐优化),但需根据任务调整。
-
资源限制:批量大小受限于硬件内存(如GPU显存),需确保不引发内存溢出(OOM)。
-
学习率联动:增大批量时,可能需要按比例增大学习率(但需谨慎,避免不稳定)。
2. 批量大小的核心权衡
| 批量大小 | 优点 | 缺点 |
|---|---|---|
| 小批量 | - 梯度噪声大,可能逃离局部最优 - 内存需求低,适合小显存设备 - 泛化性能可能更好 | - 计算效率低(并行性差) - 梯度方向波动大,训练不稳定 |
| 大批量 | - 梯度估计更准确,训练稳定 - 计算效率高(充分利用并行性) | - 易陷入平坦区域或鞍点 - 可能损害泛化性能 - 显存占用高 |
3. 确定批量大小的具体方法
(1) 基于硬件限制的调整
-
显存估算:
-
估算单个样本的显存占用(包括模型参数、激活值、梯度等)。
-
批量大小 ≈ 可用显存 / 单样本显存占用(预留20%余量)。
-
例如:单样本占用 100MB,显存 8GB → 最大批量 ≈ 8000MB / 100MB ≈ 80(取 64 或 128)。
-
(2) 基于任务特性的选择
-
数据复杂度高(如图像分割、自然语言生成):
- 建议小批量(如 16~64),以增加梯度多样性,避免过拟合。
-
数据简单或噪声多(如分类任务):
- 可尝试大批量(如 128~512),加速收敛。
(3) 学习率与批量大小的联动(线性缩放规则)
-
基本规则 :
当批量大小增大 k 倍时,学习率可同步增大 k 倍(适用于小批量→中等批量,如 32→256)。
例如:批量从 64 增大到 256,学习率从 0.1 调整到 0.4。
-
注意事项:
-
该规则在极大批量(如 >1024)时可能失效,需结合学习率预热(Learning Rate Warmup)或其他自适应优化器(如 Adam)。
-
实践公式:学习率=基础学习率×批量大小N,N 为参考批量(如 256)。
-
(4) 实验验证法
-
网格搜索 :
对候选批量(如 32、64、128、256)分别训练少量 epoch,观察:
-
训练损失下降速度
-
验证集准确率/损失
-
训练时间/显存占用
选择综合表现最优的批量。
-
-
动态调整:
-
若训练初期梯度波动大(损失震荡),可适当增大批量。
-
若模型陷入局部最优,可减小批量引入更多噪声。
-
4. 特殊情况处理
-
极小批量(Batch Size=1):
-
等价于随机梯度下降(SGD),噪声极大,需搭配低学习率或梯度累积(Gradient Accumulation)。
-
适用于显存极度受限的场景(如训练大语言模型)。
-
-
极大批量(Batch Size > 1000):
-
需结合学习率预热 (前几个 epoch 逐步增大学习率)和自适应优化器(如 LAMB、AdamW)。
-
注意:可能降低模型泛化能力,需增强正则化(如数据增强、Dropout)。
-
5. 经典场景参考
| 任务类型 | 推荐批量大小 | 理由 |
|---|---|---|
| 图像分类(ResNet) | 64~512 | 平衡并行效率与泛化性能 |
| 目标检测(YOLO) | 8~32 | 高分辨率图像显存占用大 |
| 自然语言处理(BERT) | 16~64 | 长序列导致单样本显存高 |
| 强化学习(PPO) | 64~256 | 需大量环境交互数据 |
6. 总结与建议
-
从默认值开始:尝试批量大小 64 或 128,结合学习率 0.1(SGD)或 1e-4(Adam)。
-
逐步调整:根据显存占用和训练稳定性,按 2 的倍数增减批量。
-
监控指标:重点关注验证集性能而非训练速度,避免过拟合或欠拟合。
-
结合优化器:大批量时使用 LAMB 或 AdamW,小批量时使用 SGD 或 Adam。
最终,批量大小是超参数的一种,需通过实验找到任务、模型和硬件的最优平衡点。