符号速率估计——小波变换法

@ $TOC$ 符号速率估计------小波变换法

一、原理

1.Haar小波变换

小波变换在信号处理领域被成为数学显微镜，不同于傅里叶变换，小波变换可以观测信号随时间变换的频谱特征，因此，常用于时频分析。

当小波变换前后位置处于同一个码元内或相邻两个码元相同时，其幅度是不变的，当相邻的码元不同时，小波变换的幅度值会响应变化的，其幅值常与相邻码元的幅度、相位和频率的变换有关，Haar小波可以识别出码元跳变位置，因此，可以进一步估计出数字信号的码元速率。Haar小波定义如下：
ϕ a , b ( t ) = { − 1 / a , 0 < = t < a / 2 1 / a , − a / 2 < t < 0 \phi_{a,b}(t)=\{_{-1/\sqrt{a},0<=t<a/2}^{1/\sqrt{a},-a/2<t<0} ϕa,b(t)={−1/a ,0<=t<a/21/a ,−a/2<t<0

小波变换公式如下：
W s ( a , b ) = ∫ − ∞ ∞ s ( t ) ϕ ∗ ( t − b a ) d t W_{s}(a,b)=\int_{-\infin}^{\infin}s(t)\phi^{*}(\frac{t-b}{a})dt Ws(a,b)=∫−∞∞s(t)ϕ∗(at−b)dt

其中，是 s ( t ) s(t) s(t)为平方可积信号。

2.码元速率估计过程

1）产生haar小波，小波长度为一个码元长度;

小波变换，识别码元跳变位置；

3）傅里叶变换，计算码元速率，频谱中的第一个谱峰值位置即为所求的码元速率。

二、Matlab仿真

1.代码

c 复制代码

%------Function:Estimate Symbol Rate--------
%------Remark:Using Wavelet Transform-------
%------Time:2025.04.11----------------------
%------Author:Clemence----------------------
clc;
close all;
clear all;

%------------------1.Paras----------------------------------------------
S_N = 100;      % Symbol Num
nSamp = 400;     % Samples per Symbol
N = S_N*nSamp;  % Sample Num
M = 2;          % Modulate index
f = 30;        % Signal Frequence
fs = 2000;      % Sample Frequence
ts = 1/fs;      % Sample Interval
t = 0:ts:ts*(N-1);  % Sample time

symbol = randi([0 M-1],S_N,1);  % Symbol
symbol = 2*symbol-1;            % 
symbrate = fs/nSamp;            % Symbol Rate

%------------------2.Create 2FSK Signal------------------------------------
for i=1:S_N     
    s((i-1)*nSamp+1:i*nSamp) = cos((2*pi*f+pi*symbol(i))*t((i-1)*nSamp+1:i*nSamp));
end

%-----------------3.Create Wavelet-----------------------------------------
Tb = nSamp*ts;       % Wavelet length
t = -Tb/2:ts:Tb/2;   % Wavelet Samples

phi_t = (t>-Tb/2 & t<0)-(t>0 & t<-Tb/2);


%-----------------4. Wavelet Transform-------------------------------------
for i = 1:length(s)-length(phi_t)
   x = s(i:i+length(phi_t)-1); 
   y = x.*phi_t;
   sum_y(i) = sum(y);
end

%-----------------5. plot -------------------------------------------------
figure;
subplot(2,2,1)
plot(s);
title('Original Signal')

subplot(2,2,2)
plot(t,phi_t);
title('Haar Wavelet')

subplot(2,2,3)
plot(sum_y);
title('Wavelet Transform Result')

n = length(sum_y)
inx = (0:n-1)*fs/n;

subplot(2,2,4)
plot(inx,abs(fft(abs(sum_y))));
title('Wavelet Transform Frequence')

2.仿真结果

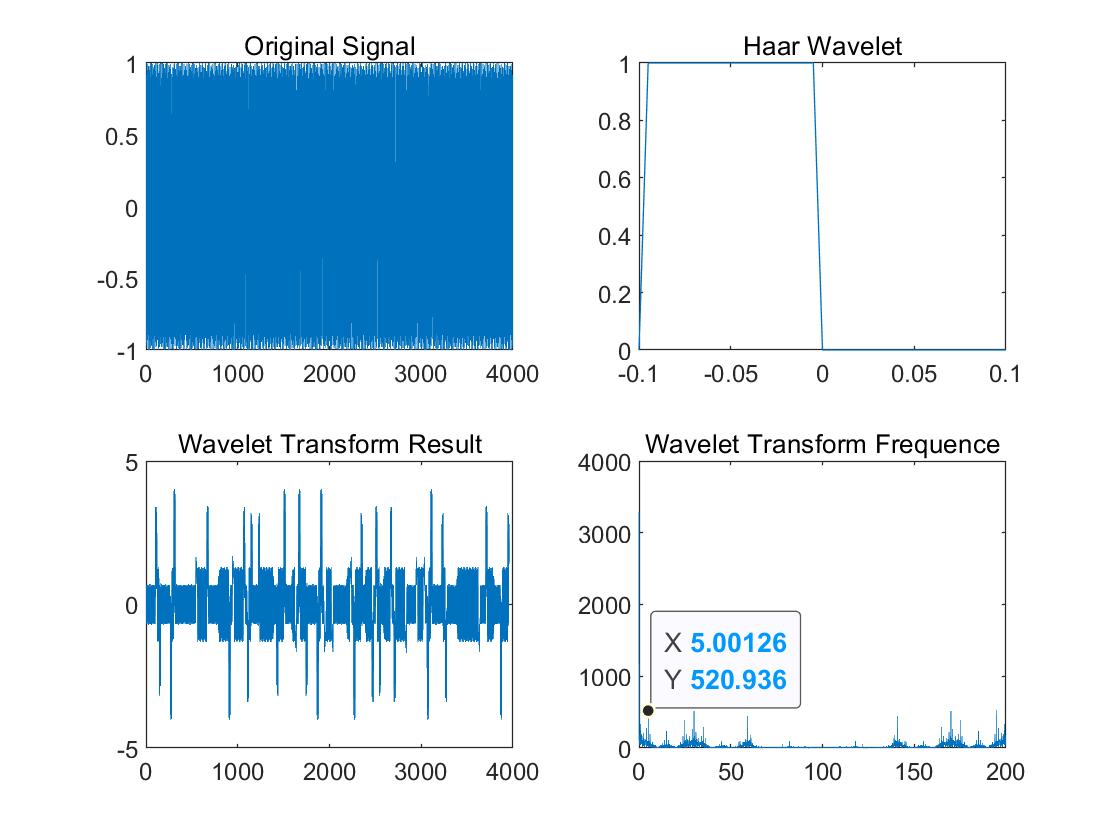
符号速率估计结果

三、总结

从仿真结果可以看出，小波变换法估计出的符号速率为5.00126，与信号的实际符号速率5基本接近，同时，符号速率估计的精度受信号的频率以及Haar小波的参数影响。