图的应用
最小生成树(最小代价树)
最小生成树是指在一个连通的无向图中,包含所有顶点的树,其所有边的权重总和在所有可能的生成树中是最小的。
应用实例
道路规划要求:所有地方都连通,且成本尽可能低
特点
同一个图可能会有多个生成树(代价相同)
如果一个连通图本身就是一棵树,那么其最小生成树就是它本身
只有连通图才有生成树,非连通图只有生成森林
Prim算法
步骤:
从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
时间复杂度:
O(|V|2) 适用于边稠密的图
kruskal算法(克鲁斯卡尔)
步骤:
每次选择一条权值最小的边,使这两条边的两头相连(原本已经联通的就不选)
直到所有点都连通
时间复杂度:
O(|E|log|E|) 适用于边稀疏的图
Prim算法的实现思想
使用isJoin[n]和lowCost[n]分别存放第n个结点是否以联通和此时到达第n个结点的最小代价
初始:从v0开始
初始化isJoin[0] = T,lowCost[0] = 0;其他结点如果与v0相连,则lowCost为权值,如果不相连,为∞
第1轮,循环遍历所有节点,找到lowCost最低且还没有加入到树的顶点
再次循环,更新还没加入的各个顶点的lowCost值
第2轮处理:循环遍历所有节点,找到lowCost最低且还没有加入到树的顶点
再次循环,更新还没加入的各个顶点的lowCost值
......
时间复杂度分析:
从v0开始需要进行n-1轮的处理 每一轮处理的时间复杂度O(2n)
kruskal算法(克鲁斯卡尔)的实现思想
初始:将各条边按权值排序
第1轮:检查第1条边的两个顶点是否已经联通(是否属于同一个集合) 不连通连起来
第2轮:检查第2条边的两个顶点是否已经联通(是否属于同一个集合) 已联通跳过
......
时间复杂度:
(如果有e条边) 总共需要进行e轮 每轮判断是否已经联通需要O(loge)的时间复杂度
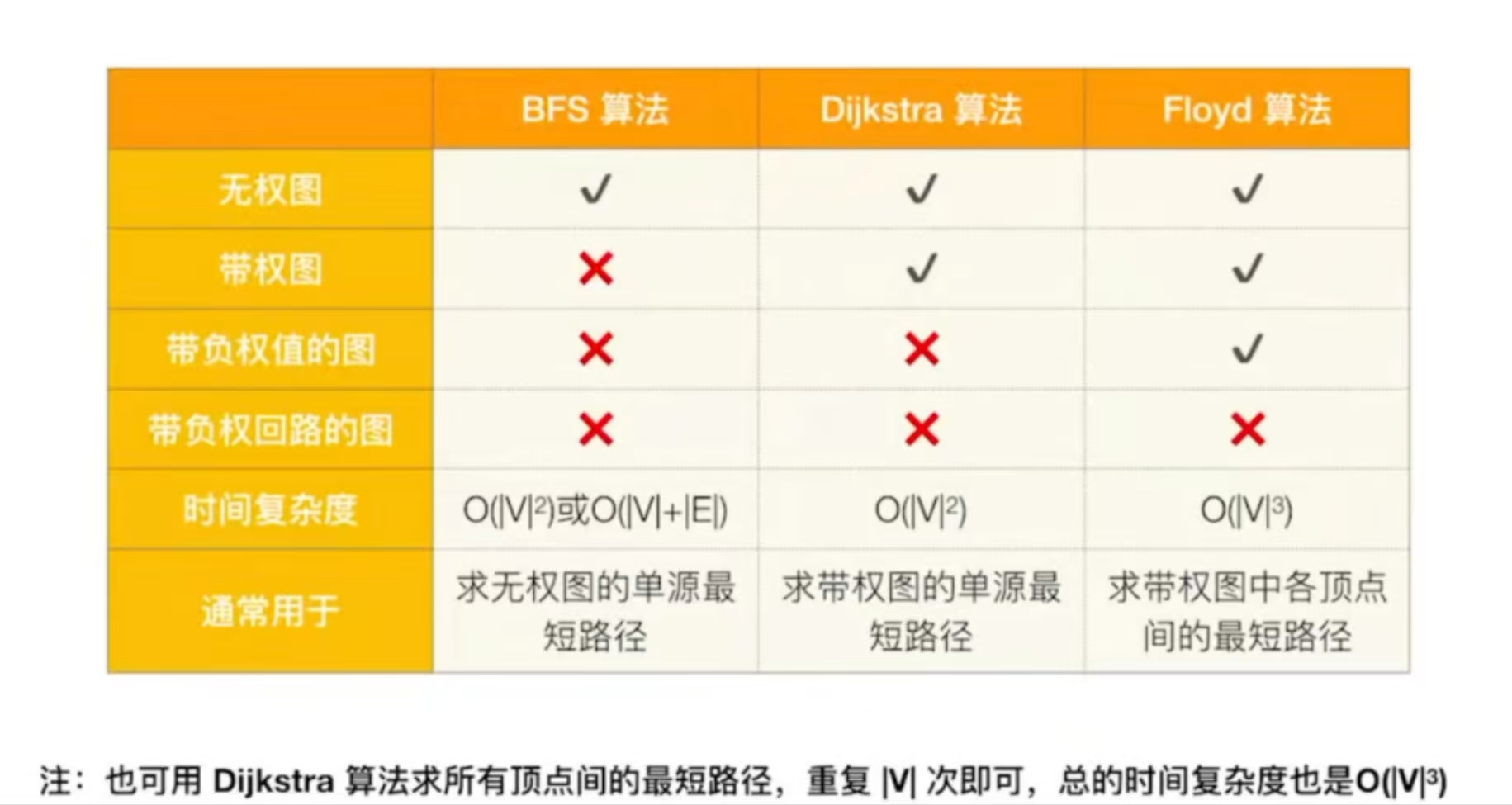
最短路径问题
单源最短路径(BFS算法、Dijistra算法)
每队顶点之间的最短路径(Floyd算法)
BFS求无权图的单源最短路径
对BFS的小修改,在visit一个顶点时,修改其最短路径长度d[]并在path[]记录前驱结点
c
bool visited[MAX_VERTEX_NUM]; //访问标记数组
void BFSTraverse(Graph G,int u){
for(i = 0;i<G.vexnum;++){
d[i] = ∞; //初始化路径长度
path[i] = -1; //最短路径从哪个顶点来
}
d[u] = 0;
visited[u] = TRUE;
EnQueue(Q,u);
while(!isEmpty(Q)){
DeQueue(Q,u); //顶点u出队列
for(w = FirstNeighbor(G,u);w>=0;w = NextNeighbor(G,u,w))
//检测u的所有邻接顶点
if(!visited[w]){ //w尚未被访问
d[w] = d[u]+1;
path[w] = u; //访问顶点w
visited[w] = true; //对w做已访问标记
EnQueue(Q,w); //顶点w入队列
}//if
}//while
}!NOTE
从顶点u起始的单源最短路径 → 以u为根的,高度最小的生成树
w的路径长度即对应在生成树中的层数
前驱结点即为其父节点
Dijistra算法求取单源最短路径
迪杰斯特拉
提出"goto有害理论" --操作系统,虚拟存储技术(小题考点 5)
信号量机制PV原语 --操作系统,进程同步(每年都考大题 15)
银行家算法 --操作系统,死锁
解决哲学家进餐问题 --操作系统,死锁(大题、小题 15)
Dijistra最短路径算法 --数据结构大题、小题(10)
BFS算法的局限性
BFS算法求取单源最短路径只适用于无权图,或者所有边权值都相同的图
Dijistra算法
final[] 标记各顶点是否已找到最短路径
dist[] 记录当前最短路径长度
path[] 记录当前最短路径上的前驱结点
步骤:
①初始化,
②第一轮:循环遍历所有节点,找到还没确定最短路径且dist最小的顶点vi,令final[i] = true
检查所有邻接自vi的顶点,若其final值为false,则更新dist和path的信息
③第二轮:循环遍历所有节点,找到还没确定最短路径且dist最小的顶点vi,令final[i] = true
检查所有邻接自vi的顶点,若其final值为false,则更新dist和path的信息
......
时间复杂度:
O(n2)即O(|V|2)
用于负权值带权图
如果带权图中有负权值,Dijistra算法会失效
Floyd算法求取顶点对间最短路径
Floyd
Floyd算法
堆排序算法
Floyd算法
使用动态规划思想,将问题分解为多个阶段
A[][] 目前来看,各顶点间的最短路径长度
path[][] 两个顶点之间的中转点
步骤:
①初始:不允许在其他顶点中转 A(-1) path(-1)
②允许在v0中转,最短路径是? 求取A(0) path(0)
③允许在v0、v1中转,最短路径是? 求取A(1) path(1)
......
时间复杂度:
从A(-1) path(-1)开始,经过n轮递推,得到A(n-1) path(n-1)
核心代码
c
//......准备工作,根据图的信息初始化矩阵A和path
//A即对应图的邻接矩阵,path全部初始化为-1
for(int k = 0;k<n;k++){ //考虑以vk为中转点
for(int i = 0;i<n;i++){ //遍历整个矩阵 行号为i 列好为j
for(int j = 0;j<n;j++){
if(A[i][j] > A[i][k]+A[k][j]){ //以vk为中转点的路径更短
A[i][j] = A[i][k]+A[k][j]; //更新最短路径长度
path[i][j] = k; //中转点
}
}
}
}时间复杂度:
O(|V|3)
空间复杂度:
O(|V|2)
可以解决带负权值的图的最短路径的求取
但是不能解决带有"负权回路"的图(有负权值的边组成的回路),这种图有可能没有最短路径