李沐动手深度学习（pycharm中运行笔记）——07.自动求导

07.自动求导（与课程对应）

1、导入torch

python 复制代码

import torch

2、假设我们想对函数 y = 2x.Tx，就是 2乘x的内积，关于列向量x求导，也就是4x

python 复制代码

x = torch.arange(4.0)  # （1）创建一个列向量 x
print("x:", x)
x.requires_grad_(True)  # （2）在我们计算 y 关于 x 的梯度之前，我们需要一个地方来存储梯度
# 等价于：x = torch.arange(4.0, requires_grad=True)
x.grad  # 默认值是None
y = 2 * torch.dot(x, x)  # （3）现在计算 y
print("y:", y)
y.backward()  # （4）通过调用反向传播函数来自动计算 y 关于 x 每个分量的梯度
x.grad  # （5）求完导数之后，通过 x.grad 来访问求完的导数
print("x.grad == 4*x:", x.grad == 4*x)  # （6）验证求导是否正确

运行结果：

3、现在让我们计算 x 的另一个函数，续上边

python 复制代码

x.grad.zero_()  # （1）在默认情况下，pytorch会累积梯度，我们需要清除之前的值；pytorch里下划线表示函数重写我的内容，此处代码表示把0写入到梯度里面
y = x.sum()
y.backward()
print("x.grad:", x.grad)

运行结果：

4、对非标量调用 backward 需要传入一个 gradient 参数，该参数指定微分函数

python 复制代码

x.grad.zero_()
y = x * x
y.sum().backward()  # 深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和
print("x.grad:", x.grad)

运行结果：

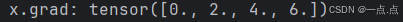
5、将某些计算移动到记录的计算图之外

python 复制代码

x.grad.zero_()
y = x * x
u = y.detach()  # 把 y 当作一个常数，而不是关于 x 的函数
z = u * x
z.sum().backward()
print("x.grad == u:", x.grad == u)

x.grad.zero_()
y.sum().backward()  # 直接 y 对 x 求导
print("x.grad == 2 * x:", x.grad == 2 * x)

运行结果：

6、即使构建函数的计算图需要通过python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度

python 复制代码

def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)  # a是个随机数，size=()代表是标量，requires_grad=True需要存储梯度
d = f(a)
d.backward()
print("d.grad:", a.grad == d / a)

运行结果：

7、完整代码：

python 复制代码

import torch

# 1、假设我们想对函数 y = 2x.Tx，就是 2乘x的内积，关于列向量x求导，就是4x
x = torch.arange(4.0)  # （1）创建一个列向量 x
print("x:", x)
x.requires_grad_(True)  # （2）在我们计算 y 关于 x 的梯度之前，我们需要一个地方来存储梯度
# 等价于：x = torch.arange(4.0, requires_grad=True)
x.grad  # 默认值是None
y = 2 * torch.dot(x, x)  # （3）现在计算 y
print("y:", y)
y.backward()  # （4）通过调用反向传播函数来自动计算 y 关于 x 每个分量的梯度
x.grad  # （5）求完导数之后，通过 x.grad 来访问求完的导数
print("x.grad == 4*x:", x.grad == 4*x)  # （6）验证求导是否正确


# 2、现在让我们计算 x 的另一个函数，续上边
x.grad.zero_()  # （1）在默认情况下，pytorch会累积梯度，我们需要清除之前的值；pytorch里下划线表示函数重写我的内容，此处代码表示把0写入到梯度里面
y = x.sum()
y.backward()
print("x.grad:", x.grad)


# 3、对非标量调用 backward 需要传入一个 gradient 参数，该参数指定微分函数
x.grad.zero_()
y = x * x
y.sum().backward()  # 深度学习中，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和
print("x.grad:", x.grad)


# 4、将某些计算移动到记录的计算图之外
x.grad.zero_()
y = x * x
u = y.detach()  # 把 y 当作一个常数，而不是关于 x 的函数
z = u * x
z.sum().backward()
print("x.grad == u:", x.grad == u)

x.grad.zero_()
y.sum().backward()  # 直接 y 对 x 求导
print("x.grad == 2 * x:", x.grad == 2 * x)


# 即使构建函数的计算图需要通过python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度
def f(a):
    b = a * 2
    while b.norm() < 1000:
        b = b * 2
    if b.sum() > 0:
        c = b
    else:
        c = 100 * b
    return c

a = torch.randn(size=(), requires_grad=True)  # a是个随机数，size=()代表是标量，requires_grad=True需要存储梯度
d = f(a)
d.backward()
print("d.grad:", a.grad == d / a)

如果此文章对您有所帮助，那就请点个赞吧，收藏+关注那就更棒啦，十分感谢！！！