C++:BST、AVL、红黑树

二叉搜索树（BST）
二叉平衡搜索树（AVL）
红黑树（RBT）
三者对比
什么情况下使用？
[C++ 标准库中的使用](#C++ 标准库中的使用)
总结

二叉搜索树（BST）

二叉搜索树（Binary Search Tree），是一种二叉树，其每个节点满足以下性质：

左子树中所有节点的值小于当前节点的值
右子树中所有节点的值大于当前节点的值
左右子树也必须是二叉搜索树

在C++中简单结点的定义：

cpp 复制代码

struct Node {
    int data;
    Node* left;
    Node* right;
    Node(int val) : data(val), left(nullptr), right(nullptr) {}
};

作用:

高效查找：通过比较值，可以快速定位某个值是否存在（平均 O(log n) 时间，n 为节点数）。
插入/删除：支持动态插入和删除节点。
有序遍历：中序遍历 BST 可以得到节点值的升序序列。

适用场景:

需要频繁查找、插入、删除的场景，且数据量较小或数据分布均匀。
适合简单的键值存储或需要维护有序数据的应用。

缺点:

不平衡：如果插入顺序接近有序（例如全递增或递减），BST 会退化为链表，导致查找、插入、删除时间复杂度恶化为 O(n)。
因此，BST 在实际应用中常被更高级的平衡树（如 AVL 树或红黑树）替代。

二叉平衡搜索树（AVL）

二叉平衡搜索树（AVL）是一种自平衡二叉搜索树，由苏联数学家Adelson-Velsky和Landis发明。

除了满足BST的性质外，AVL树还保证：

每个节点的左右子树高度差（平衡因子）不超过1（即|左子树高度-右子树高度|<=1）。
通过旋转操作（左旋、右旋、左右旋、右左旋）在插入或删除后恢复平衡。

在C++中简单结点的定义：

cpp 复制代码

struct AVLNode {
    int data;
    AVLNode* left;
    AVLNode* right;
    int height; // 记录节点高度
    AVLNode(int val) : data(val), left(nullptr), right(nullptr), height(1) {}
};

作用：

高效操作：由于高度平衡，查找、插入、删除的时间复杂度稳定为 O(log n)，不会退化链表。
严格平衡：适合需要极高查询性能的场景。

适用场景：

适合查询频繁的场景，例如数据库索引、内存中的键值存储。
需要严格平衡的应用，例如某些实时系统。

缺点：

维护开销高：插入和删除操作可能触发多次旋转，维护平衡的代价较高。
不适合频繁修改：如果插入/删除远多于查询，旋转的开销可能影响性能。

红黑树（RBT）

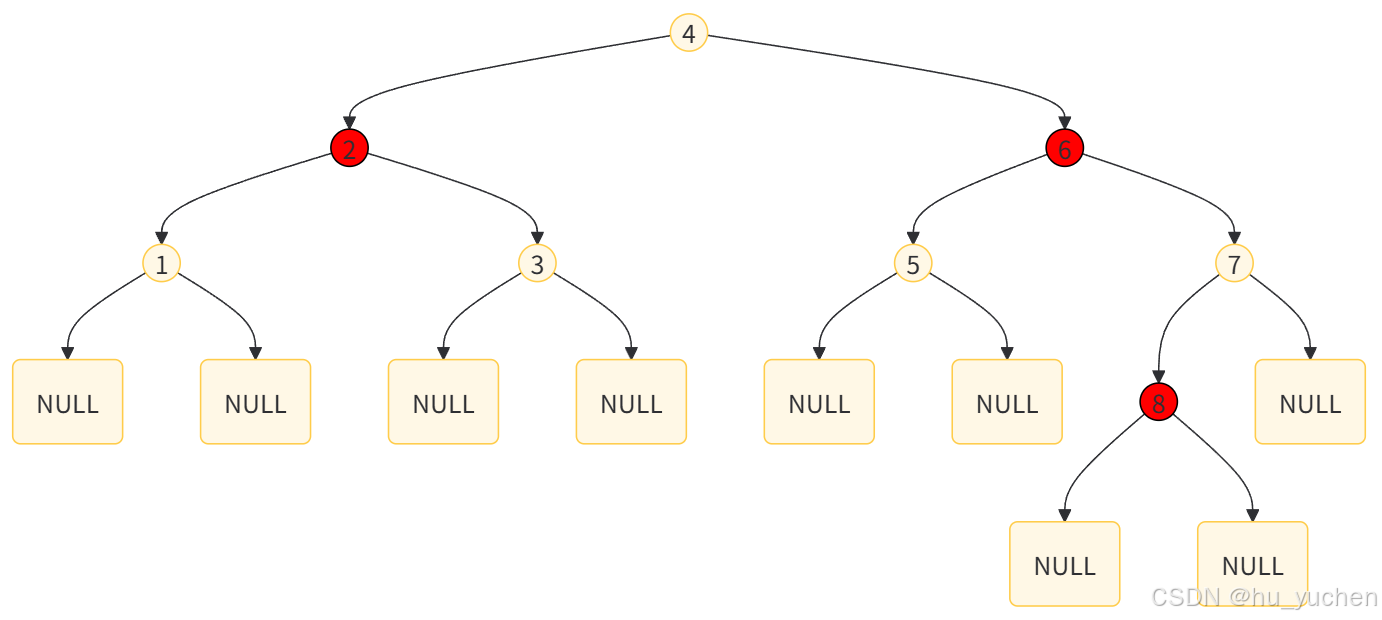
红黑树（Red-Black-Tree）是一种自平衡二叉搜索树，通过颜色约束（红/黑）来保证近似平衡。红黑树满足以下性质：

每个节点是红色或黑色
根节点是黑色
所有叶子节点（NIL哨兵节点，空节点）是黑色
红色节点的子节点必须是黑色（即不能有连续的红色节点）
从任一节点到其每个叶子节点的路径上，黑色节点数量相同（黑色高度相同）

通过旋转和颜色调整 维持平衡

在C++中简单结点的定义：

cpp 复制代码

enum Color { RED, BLACK };

struct RBNode {
    int data;
    RBNode* left;
    RBNode* right;
    RBNode* parent; // 红黑树需要父节点指针
    Color color;
    RBNode(int val) : data(val), left(nullptr), right(nullptr), parent(nullptr), color(RED) {}
};

作用：

高效且灵活：查找、插入、删除的时间复杂度为 O(log n)，但比 AVL 树更适合频繁修改。
广泛应用：红黑树是许多标准库（如 C++ STL 的 std::map 和 std::set）的底层实现。

适用场景：

适合频繁插入和删除的场景，例如：
- C++ STL 容器（std::map, std::set）。
- 操作系统中的内存管理和调度算法。
- 数据库和文件系统中需要动态维护有序数据的结构。
需要适度平衡的场景，红黑树比 AVL 树更宽松，维护成本更低。

缺点：

查询性能略逊：由于红黑树不如 AVL 树严格平衡，查询性能可能略低于 AVL 树（但差异不大）。
实现复杂：红黑树的插入和删除涉及颜色调整和旋转，代码实现比 BST 和 AVL 树更复杂。

三者对比

特性	BST（二叉搜索树）	AVL 树	红黑树
平衡性	无平衡机制，可能退化为链表	严格平衡（高度差 ≤ 1）	近似平衡（最长路径 ≤ 2×最短路径）
时间复杂度	查找/插入/删除：O(log n) ~ O(n)	查找/插入/删除：O(log n)	查找/插入/删除：O(log n)
维护开销	低，无需平衡操作	高，频繁旋转	中等，旋转和颜色调整
查询性能	不稳定，取决于树形	最高，严格平衡	高，略逊于 AVL 树
插入/删除性能	较高（无平衡开销）	较低（频繁旋转）	高（较少旋转）
实现复杂度	简单	中等	复杂
典型应用	简单键值存储，静态数据	查询密集型应用（如数据库索引）	STL 容器，动态数据维护

什么情况下使用？

选择 BST：
- 数据量小，或者插入顺序随机（树形较平衡）。
- 实现简单，不需要复杂平衡机制。
- 例如：教学用途、原型开发、静态数据集的简单查询。
选择 AVL 树：
- 查询远远多于插入/删除 的场景，因为 AVL 树的高度最优。
- 需要严格的 O(log n) 查询性能。
- 例如：数据库索引、实时系统中的键值查找。
选择红黑树：
- 插入和删除频繁，需要动态维护有序数据。
- 希望在查询和修改之间取得平衡。
- 例如：C++ STL 的 std::map 和 std::set、操作系统调度、文件系统元数据管理。

C++ 标准库中的使用

C++ STL 的 std::map 和 std::set 通常基于 红黑树 实现，因为红黑树在动态操作中表现均衡。
如果需要 AVL 树或普通 BST，需要自己实现或使用第三方库（如 Boost）。
实现建议：
- BST：适合初学者练习树结构。
- AVL 树：需要掌握旋转操作（单旋、双旋）。
- 红黑树：需要理解颜色调整和复杂情况，建议参考 STL 源码或成熟实现。

总结

BST：简单但不平衡，适合小规模或静态数据。
AVL 树：严格平衡，查询性能最佳，适合查询密集场景。
红黑树：近似平衡，插入/删除高效，适合动态数据维护，是实际应用中最常用的平衡树。