机器学习-08-时序数据分析预测

参考

时间序列预测模型比较分析：SARIMAX、RNN、LSTM、Prophet 及 Transformer

https://mp.weixin.qq.com/s/b4IE-y85zHoW1Ujuy9hDGg

"欣旺达"股价的时序预测（Tushare + Prophet）

时序数据与非时序数据的主要区别在于数据的结构和依赖关系。理解这两者的差异对于选择合适的数据处理方法和模型至关重要。

CICC科普栏目｜时间序列预测的常用方法优缺点对比分析

时序数据 vs 非时序数据的差异与算法选择

时序数据 vs 非时序数据

1. 数据结构

   • 时序数据：具有时间顺序，每个数据点都有一个明确的时间戳，且通常相邻的数据点之间存在相关性（即自相关性）。例如，股票价格、气象数据等。
   • 非时序数据：没有固有的时间顺序，数据点之间的关系不是基于时间的。例如，客户信息、图像分类中的像素值等。

2. 依赖关系

   • 时序数据：数据点之间可能存在时间上的依赖关系，这意味着当前时刻的状态可能受到过去状态的影响。这种特性要求模型能够捕捉到这些依赖关系。
   • 非时序数据：数据点之间通常是独立同分布（i.i.d），也就是说，每个样本都是独立于其他样本，并且来自相同的概率分布。

3. 特征工程

   • 时序数据：经常需要进行特定的特征提取或转换，如滑动窗口、滞后特征（lag features）、差分（differencing）以消除趋势和季节性成分等。
   • 非时序数据：特征工程更多关注于如何从原始数据中提取有意义的信息，比如PCA降维、特征选择等。

4. 预测目标

   • 时序数据：通常用于预测未来的值，这涉及到理解数据中的趋势、周期性和随机波动。
   • 非时序数据：主要用于分类或回归任务，不涉及未来预测的问题。

常见的时序算法

参考：CICC科普栏目｜时间序列预测的常用方法优缺点对比分析

时间序列预测是指利用获得的数据按时间顺序排成序列，分析其变化方向和程度，从而对未来若干时期可能达到的水平进行推测。时间序列预测的基本思想，就是将时间序列作为一个随机变量的一个样本，用概率统计的方法，从而尽可能减少偶然因素的影响。

当比较时间序列预测的常用方法时，可以考虑它们的优点和缺点，以便选择最适合的方法。

移动平均法（MA）：

优点：简单易懂，易于实现；能够平滑数据并捕捉数据的长期趋势；能够处理季节性变动。

缺点：只利用了过去的有限观测，忽略其他影响因素；对离群值敏感；未考虑数据非线性关系。

加权移动平均法（WMA）：

优点：能够更灵活地对过去值赋予不同的权重，以适应不同的数据情况；能够处理季节性变动。

缺点：对权重的选择敏感；对离群值敏感；未考虑数据的非线性关系。

指数平滑法（ES）：

优点：简单易懂易于实现；能够平滑数据并捕捉数据长期趋势；能够自动适应数据的时间变化。

缺点：只利用了过去的有限观测，忽略了其他影响因素；对初始值的选择敏感；未考虑数据的非线性关系。

季节性模型方法：

优点：能够处理季节性变动，捕捉周期性的影响；可以提供季节性调整后的预测结果。

缺点：需要对季节性的周期和幅度有一定的先验知识；对于非周期性的数据预测效果较差。

自回归滑动平均模型（ARMA）：

优点：能够自动捕捉时间序列数据的趋势和周期性；可以处理非平稳数据。

缺点：对模型参数的选择需借助自相关图（ACF）和偏自相关图（PACF），有一定主观性；对离群值敏感。

自回归积分滑动平均模型（ARIMA）：

优点：能够处理非平稳数据，对趋势和周期性进行建模；相对于ARMA模型，可以更好地处理非平稳数据。

缺点：对模型参数的选择需要通过查看自相关图和偏自相关图；对于长期的趋势和季节性变动不适用。

随机森林（Random Forest）：

优点：能够处理多个变量之间的非线性关系；对于大规模数据和高维数据具有较好的扩展性；能够提供特征重要性排序。

缺点：对于时间序列数据，可能需要进行一些预处理，如滑动窗口方法；参数选择较为复杂；模型解释性较差。

神经网络（Neural Network）：

优点：能够处理非线性关系和复杂的时间序列数据；适用于大规模数据的建模和预测；具有一定的自适应性。

缺点：模型参数调整较为困难；数据量和计算资源的要求较高；对于小样本数据可能会过拟合。

长短期记忆网络（LSTM）：

优点：适用于处理长期依赖关系和非线性关系；能够捕捉序列数据中的长期模式和短期波动；对于大规模数据和高维数据有较好的扩展性。

缺点：对于小样本数据可能会过拟合；模型参数的选择和调整较为复杂；对计算资源需求较高。

卷积神经网络（CNN）：

优点：适用于处理具有空间结构的时间序列数据，如图像、声音等；能够捕捉序列数据中的局部模式和特征；对于大规模数据和高维数据有较好的扩展性。

缺点：对于非平稳数据和长期依赖关系的建模相对不足；对于数据的前后关系可能不够充分。

支持向量回归（SVR）：

优点：能够处理非线性关系；对于小样本数据有较好的表现；通过核函数的选择可以适应不同的数据情况。

缺点：对于大规模数据和高维数据的处理较为困难；需要调整超参数，如选择合适的核函数和正则化参数；对离群值敏感。

强化学习：

优点：能够通过与环境的交互来优化预测策略，适用于动态环境的时间序列预测；对于复杂问题和非线性关系有潜力提供较好的解决方案。

缺点：需要大量的训练样本和计算资源；对于任务设定和奖励设计有一定的挑战；对模型的解释性较差。

集成方法：

优点：能够通过组合多个预测模型的结果来提高准确性和稳定性；能够综合不同模型的优势。

缺点：对于模型的选择和集成方式需要一定的经验和判断；对计算资源和训练时间的要求较高。

贝叶斯方法：

优点：能够估计预测的不确定性，提供可信度的区间估计；能够自动更新模型参数和先验概率。

缺点：计算复杂度较高，对于大规模数据可能不适用；对先验知识的依赖性较强；无法处理非线性关系和复杂模型。

随机游走模型：

优点：简单易懂，简单地假设未来值与当前值相等，适用于短期预测。

缺点：没有利用过去的信息，只能作为基准模型；对于长期预测效果较差；无法捕捉趋势和季节性的影响。

非线性时间序列模型：

优点：

能够处理复杂的非线性关系，适用于特定的非线性时间序列数据；有较好的灵活性和泛化能力。

缺点：建模复杂度较高，参数估计和模型解释较为困难；对数据量和计算资源的要求较高；需要充分的领域知识和经验去选择和调整模型。

因子分析：

优点：能够将复杂的时间序列数据分解为主要的共同模式和影响因子；提供有关数据生成过程的进一步理解。

缺点：对数据的先验假设和可解释性要求较高；需要充分的领域知识和经验来解释因子

使用传统集成学习算法预测时序数据的效果

传统的集成学习算法，如随机森林（Random Forest）、梯度提升树（Gradient Boosting Trees, GBM）、XGBoost等，在设计上主要是为了解决非时序数据问题。然而，它们也可以应用于时序数据分析，但效果可能会因以下原因而受限：

• 缺乏对时间序列特性的直接建模能力：这些算法本质上并不考虑输入特征之间的时间顺序，因此不能直接利用时序数据中的自相关性。

• 需要手动特征工程：为了使集成学习算法有效地处理时序数据，通常需要进行大量的预处理工作，包括创建滞后特征、移动平均值、滚动窗口统计量等。这样做可以部分地补偿模型在捕捉时间依赖性方面的不足。

• 性能限制：尽管通过适当的特征工程，集成学习算法可以在某些情况下表现良好，但对于高度动态或者复杂的时间序列（特别是那些包含长期依赖关系的情况），深度学习模型（如LSTM、GRU）或其他专门针对时序数据设计的方法（如ARIMA、Prophet）往往能提供更好的性能。

结论

虽然使用传统的集成学习算法来预测时序数据是可行的，但其效果可能不如专门为时序分析设计的方法好。对于较为简单的时间序列问题，经过恰当的特征工程后，集成学习算法仍能给出不错的预测结果；然而，面对复杂的时序模式，尤其是当数据表现出强烈的周期性或长程依赖时，采用更适合处理时序数据的技术将是更优的选择。

依赖库

依赖包statsmodels

安装依赖包statsmodels

pip install statsmodels==0.14.4

statsmodels` 是一个强大的 Python 库，主要用于统计建模和计量经济学分析。在时间序列分析中，它特别有用，主要功能包括：

1. 统计检验 ：
   • 如你代码中的 adfuller (ADF检验)，用于检验时间序列的平稳性
   • 其他假设检验（t检验、F检验等）
2. 时间序列分析 ：
   • 自相关函数（ACF）和偏自相关函数（PACF）计算
   • ARIMA、SARIMA等时间序列模型
   • 状态空间模型
3. 回归分析 ：
   • 线性回归
   • 广义线性模型
   • 稳健回归
4. 可视化工具 ：
   • 统计图形绘制（如你代码中的ACF/PACF图）

在你的时间序列分析场景中，statsmodels 提供了完整的工具链：从平稳性检验(ADF) → 自相关分析(ACF/PACF) → 建模(ARIMA等) → 预测。

依赖包torch

pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple

案例

时间序列预测根据过去的模式预测未来事件。我们的目标是找出最佳预测方法，因为不同的技术在特定条件下表现出色。

我们将探讨五种主要方法：

• SARIMAX：检测重复出现的模式并考虑各种外部影响。
• RNN： 分析顺序数据，适用于按时间顺序排列的信息。
• LSTM：通过长时间保留数据来增强 RNN。
• Prophet： 由 Facebook 开发，对数据缺口和重大趋势变化具有强大的抵抗能力。
• Transformer： 利用自我关注，有效识别复杂模式。

我们在不同类型的数据上对这些方法进行了测试：

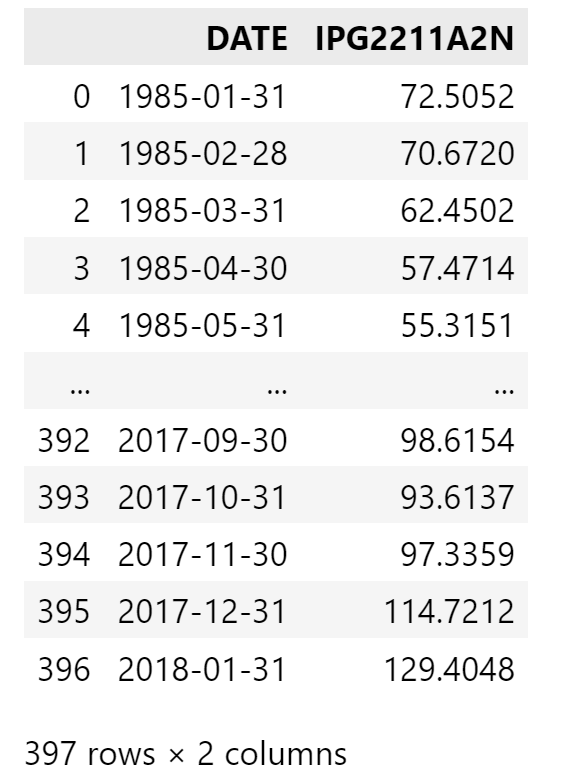
1\] [电力生产Kaggle 数据集](https://www.kaggle.com/datasets/shenba/time-series-datasets?select=Electric_Production.csv) Electric_Production.csv \[2\] [洗发水销售Kaggle 数据集](https://www.kaggle.com/datasets/redwankarimsony/shampoo-saled-dataset) shampoo_sales.csv #### **时序数据预测一般方法** > **数据审查：** > > 首先进行的是对数据趋势的初步评估，通过自相关函数（ACF）和部分自相关函数（PACF）的分析来识别其中的模式。这个步骤对于发现数据中的周期性规律至关重要，能够为后续模型的选择及其参数设定提供依据。 > **参数调优：** > > 根据所使用的算法以及特定的数据集特性，仔细调整参数以提升预测的精确度。这一过程是确保模型性能的关键步骤。 > **模型训练与验证：** > > 拆分数据集为训练集验证集和测试集，训练算法，检验模型的有效性和准确性。 > **效果评估：** > > 采用平均绝对百分比误差（MAPE）作为统一的评价标准，对所有验证数据的表现进行衡量，从而实现不同算法间的直接对比。 此方法不仅有助于深入理解各算法的特性和局限性，还能够指导我们在面对具体的时间序列预测问题时，做出更为明智的算法选择。 #### **电力数据-数据审查** 我们使用 "电力生产 "数据集探索时间序列识别。我们的目标是计算该数据的月平均值，从而发现准确预测所必需的关键趋势和模式。 下面的 Python 脚本将对月度数据汇总进行处理和可视化： import matplotlib.pyplot as plt import pandas as pd data = pd.read_csv("Electric_Production.csv") data.info() data 输出如下： >  转换数据类型 #把data的Date类型转换为datetime类型 data['DATE'] = pd.to_datetime(data['DATE']) # 设置日期为索引 data.set_index('DATE', inplace=True) data.info() data 输出如下： >  绘制电力数据分布 # data.IPG2211A2N的作用是将数据按照月为单位进行重采样，然后计算每个月的平均值。 # 最后，使用plot()函数将重采样后的数据绘制为折线图。 # ME表示月的结尾，即每个月的最后一天。 # 例如，如果数据的时间范围是2010年1月1日到2020年12月31日， # 那么重采样后的数据将包含2010年1月到2020年12月的每个月的平均值。 monthly_data = data.IPG2211A2N.resample('ME').mean() data.IPG2211A2N.resample('ME').mean().plot() plt.show() 输出如下： >  该图（图 1）揭示了电力生产的潜在季节性变化，这对预测工作至关重要。 为了评估数据集的静态性并探索自回归和移动平均成分，我们进行了统计测试和分析，如 Dickey-Fuller 检验、自相关函数 (ACF) 和偏自相关函数 (PACF)： from statsmodels.tsa.stattools import adfuller, acf, pacf # 假设 monthly_data 是你的时间序列数据 # Dickey-Fuller test 的意思是： # 1. 首先，我们需要对时间序列数据进行平稳性检验。 # 2. 平稳性检验的目的是判断时间序列数据是否具有单位根，即是否存在自相关性。 # 3. 单位根的存在意味着时间序列数据不是平稳的，即存在趋势或季节性。 # 4. 平稳性检验的方法是使用 Dickey-Fuller 检验。 # 5. Dickey-Fuller 检验的原理是： # 1. 首先，我们需要对时间序列数据进行差分。 # 2. 然后，我们需要对差分后的数据进行平稳性检验。平稳性检验的目的是判断时间序列数据是否具有单位根，即是否存在自相关性。 单位根的存在意味着时间序列数据不是平稳的，即存在趋势或季节性。 # 3. 如果差分后的数据是平稳的，那么原始时间序列数据也是平稳的。 # 4. 如果差分后的数据不是平稳的，那么原始时间序列数据也不是平稳的。 # 6. 因此，我们可以使用 Dickey-Fuller 检验来判断时间序列数据是否具有单位根。 # 7. 如果时间序列数据具有单位根，那么我们可以使用 ARIMA 模型来进行预测。 # 8. 如果时间序列数据不具有单位根，那么我们可以使用 ARMA 模型来进行预测。 """ ADF的中文含义是： ADF Statistic: -2.25699035004725 # 这个值越小，说明时间序列数据越平稳 p-value: 0.18621469116586592 # 这个值越小，说明时间序列数据越平稳 如果 ADF Statistic 小于临界值，并且 p-value 小于 0.05，那么我们可以认为时间序列数据是平稳的。 如果 ADF Statistic 大于临界值，并且 p-value 大于 0.05，那么我们可以认为时间序列数据不是平稳的。 """ result = adfuller(monthly_data) print(f'ADF Statistic: {result[0]}') print(f'p-value: {result[1]}') 输出如下： > ADF Statistic: -2.25699035004725 > > p-value: 0.18621469116586592 输出ACF和PACF # ACF and PACF acf_values = acf(monthly_data, nlags=20) pacf_values = pacf(monthly_data, nlags=20, method='ols') # print ACF and PACF print("ACF values:", acf_values) print("PACF values:", pacf_values) 输出如下 > ACF values: \[1. 0.86277906 0.63640377 0.52487459 0.61398953 0.8028675 0.88986545 0.78414523 0.58354441 0.488432 0.5944013 0.7975361 0.90427102 0.7819278 0.56651747 0.46030659 0.55354872 0.73918453 0.82055665 0.7169618 0.52063329

PACF values: [ 1. 0.87824247 -0.47155784 0.61231867 0.57390709 0.44843605 0.08025808 -0.07429707 -0.13776652 0.19178424 0.3639721 0.47006531 0.45728639 -0.32745944 -0.01895411 -0.13384899 0.169511 0.07304471 0.01284553 0.0627973 -0.04673421]

可视化ACF和PACF

# ACF and PACF
acf_values = acf(monthly_data, nlags=20)
pacf_values = pacf(monthly_data, nlags=20, method='ols')

# Visualization
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.plot(acf_values)
plt.title('Autocorrelation Function')
plt.subplot(122)
plt.plot(pacf_values)
plt.title('Partial Autocorrelation Function')
plt.tight_layout()
plt.show()

输出如下：

这些分析提供了以下结果：

• Dickey-Fuller 检验： 显示非平稳性，表明需要进行差分。
• ACF 和 PACF： 突显了自回归和移动平均成分的必要性，建议使用初始 ARIMA（1,1,0）模型。

这些发现使我们能够准确地准备和评估各种数据集，以便进行时间序列预测。

电力数据-预测技术

利用 SARIMAX 进行时间序列预测

确定数据集的 ARIMA 模型参数后，我们就可以使用 SARIMAX 进行预测了。SARIMAX 代表带有外生因素的季节性自回归整合移动平均模型，通过纳入季节周期和外部变量的潜在影响来增强 ARIMA。

下面是将 SARIMAX 应用于 "电力生产" 数据集的 Python 示例，其中保留了最近三个月的数据以进行验证：

import pandas as pd
from statsmodels.tsa.statespace.sarimax import SARIMAX
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.arima.model import ARIMA

data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

输出如下：

预测

from sklearn.metrics import mean_absolute_percentage_error
# 将数据分成训练集和测试集

train_data = monthly_data['IPG2211A2N'][:-3]
test_data = monthly_data['IPG2211A2N'][-3:]

# 拟合 ARIMA(1,1,1) 模型
model = ARIMA(train_data, order=(1,1,1))
model_fit = model.fit()

# 预测过去三个月
forecast = model_fit.forecast(steps=3)
# 计算实际值和预测值之间的 MAPE
mape = mean_absolute_percentage_error(test_data, forecast)
print(f"Forecast: {forecast}")
print(f"Actual: {test_data}")
print(f"MAPE: {mape}")

输出如下：

我们使用平均绝对百分比误差 (MAPE) 作为评估预测准确性的指标。同样的方法可应用于其他数据集，从而确保我们预测方法的一致性。

使用 ARIMA 修改为使用 SARIMAX

要将上述代码从使用 ARIMA 修改为使用 SARIMAX，需要对模型的定义和拟合部分进行调整。以下是修改后的代码：

from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.statespace.sarimax import SARIMAX

# 将数据分成训练集和测试集
train_data = monthly_data['IPG2211A2N'][:-3]
test_data = monthly_data['IPG2211A2N'][-3:]

# 拟合 SARIMAX(1,1,1) 模型
model = SARIMAX(train_data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))
model_fit = model.fit()

# 预测过去三个月
forecast = model_fit.forecast(steps=3)

# 计算实际值和预测值之间的 MAPE
mape = mean_absolute_percentage_error(test_data, forecast)
print(f"Forecast: {forecast}")
print(f"Actual: {test_data}")
print(f"MAPE: {mape}")

主要修改点：

1. 导入 SARIMAX ：从 statsmodels.tsa.statespace.sarimax 导入 SARIMAX。
2. 替换 ARIMA 为 SARIMAX ：将 ARIMA 替换为 SARIMAX。
   • order=(1, 1, 1) 表示非季节性部分的 (p, d, q) 参数。
   • seasonal_order=(0, 0, 0, 0) 表示没有季节性成分（如果需要季节性成分，可以调整这些参数）。
3. 保持其他逻辑不变：包括数据分割、预测和 MAPE 计算。

注意事项：

• 如果你的数据具有季节性模式，可以调整 seasonal_order 参数。例如，如果数据具有 12 个月的季节性周期，可以设置 seasonal_order=(1, 0, 1, 12)。
• SARIMAX 是 ARIMA 的扩展版本，支持更复杂的建模需求，如外生变量和季节性成分。

利用 RNN 进行时间序列预测

递归神经网络（RNN）在时间序列预测中表现突出，因为它能通过隐藏状态动态记忆过去的信息。这与 SARIMAX 的线性建模方法形成鲜明对比，因为 RNN 可以以非线性方式对数据进行建模，使其在理解和预测随时间变化的模式方面表现出色。

下面，我们使用 RNN 对 "电力生产" 数据集进行预测，特别是针对过去三个月的数据进行验证，以评估模型的预测性能。

导入库并加载数据

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

输出如下：

数据探索

查看数据的趋势

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

输出如下：

查看趋势 (Trend) 、季节性 (Seasonality) 和 残差 (Residual)。

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

输出如下：

seasonal_decompose() 是 statsmodels 中用于时间序列分解的工具，它将时间序列分解为三个主要成分：趋势 (Trend) 、季节性 (Seasonality) 和 残差 (Residual) 。通过调用 .plot() 方法，可以生成这些成分的可视化图表。

以下是分解图的解读方法：

---

1. 原始数据 (Observed)

• 这是输入的时间序列数据，表示实际观测值。
• 观察这部分可以帮助你了解数据的整体变化趋势和波动情况。
• 如果数据有明显的周期性或长期趋势，可以在这一部分初步观察到。

---

2. 趋势 (Trend)

• 趋势部分反映了时间序列中的长期变化模式。
• 它通常是通过平滑技术（如移动平均）提取出来的。
• 如何看：
  • 如果趋势线向上倾斜，说明数据有增长趋势。
  • 如果趋势线向下倾斜，说明数据有下降趋势。
  • 如果趋势线接近水平，说明数据没有明显的长期趋势。

---

3. 季节性 (Seasonality)

• 季节性部分反映了时间序列中的周期性波动。
• 它通常是通过从数据中去除趋势和残差后提取出来的。
• 如何看：
  • 如果季节性成分呈现周期性的波形（如正弦曲线），说明数据具有季节性模式。
  • 波动的周期长度可以反映季节性的时间跨度（例如，12个月的周期可能表示年度季节性）。
  • 如果季节性成分接近一条直线（没有明显波动），说明数据可能没有显著的季节性。

---

4. 残差 (Residual)

• 残差部分是原始数据减去趋势和季节性后的剩余部分。
• 它反映了模型无法解释的随机噪声或异常波动。
• 如何看：
  • 如果残差在零附近随机波动且幅度较小，说明模型对数据的拟合较好。
  • 如果残差中存在明显的模式（如趋势或周期性），说明模型可能没有完全捕捉到数据的趋势或季节性。
  • 如果残差的波动幅度较大，说明数据中可能存在更多的噪声或异常值。

---

示例解读

假设你有一个月度销售数据的时间序列，使用 seasonal_decompose().plot() 得到以下结果：

1. Observed: 数据整体呈上升趋势，并且每年的某些月份（如12月）有明显的高峰。
2. Trend: 趋势线显示销售数据逐年增长。
3. Seasonality: 季节性成分显示每年的12月有显著的高峰，而其他月份相对平稳。
4. Residual: 残差部分在零附近随机波动，但偶尔有一些较大的异常值，可能对应特殊事件（如促销活动）。

---

注意事项

1. 分解方法的选择：

   • seasonal_decompose() 默认使用加法分解 (model='additive')，即假设时间序列是由趋势、季节性和残差相加而成。

   • 如果数据的季节性波动随趋势增大而增大，可以选择乘法分解 (model='multiplicative')。

   • 代码示例：

     from statsmodels.tsa.seasonal import seasonal_decompose
     result = seasonal_decompose(data, model='multiplicative', period=12)
     result.plot()

2. 周期参数 (period)：

   • period 参数指定了季节性周期的长度。例如，月度数据通常设置为 12（一年12个月），每日数据可能设置为 7（一周7天）。
   • 如果未指定 period，可能会导致分解失败或结果不准确。

3. 残差分析：

   • 残差应该接近白噪声（随机分布）。如果残差中仍有模式，可能需要更复杂的模型（如 SARIMA）来捕捉剩余的结构。

---

通过以上步骤，你可以全面理解时间序列的特性，并为进一步建模（如 ARIMA 或 SARIMAX）提供依据。

数据处理

分解以去除季节性成分并查看

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

输出如下：

对数据进行归一化处理

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

输出如下：

将数据转换为序列

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

输出如下：

拆分数据集并转换数据

拆分训练集和测试集

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

输出如下：

(381, 12, 1) (3, 12, 1) (381, 1) (3, 1)

把数据转换为tensor

# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)

输出如下：

torch.Size([381, 12, 1]) torch.Size([381])

torch.Size([3, 12, 1]) torch.Size([3])

定义一个RNN模型

class SimpleRNN(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(SimpleRNN, self).__init__()
        self.hidden_layer_size = hidden_layer_size
        self.rnn = nn.RNN(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
        predictions = self.linear(rnn_out.view(len(input_seq), -1))
        return predictions[-1]

model = SimpleRNN()
criterion = nn.MSELoss()

optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

训练模型

# 训练模型
epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')

输出如下

评估模型

# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')

输出如下：

Predicted: 0.6018507480621338, Actual: 0.5403230786323547

Predicted: 0.6018507480621338, Actual: 0.5707471966743469

Predicted: 0.6018507480621338, Actual: 0.7388026118278503

计算MAPE的值

# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

输出如下:

MAPE: 2.1545194169134567%
以下是简化代码概述：

• 预处理： 调整季节性并规范化数据，为 RNN 做准备。
• 序列准备： 将数据转换为序列，用于 RNN 训练，模拟时间依赖关系。
• RNN 架构： 利用 RNN 层进行时间处理，利用线性层进行预测。
• 训练： 在历时上迭代以最小化损失，并通过反向传播更新模型。
• 预测： 应用所学模式预测测试集的未来值。
• 反变换： 将预测值调整回原始比例，以供评估。
• 准确度评估： 采用 MAPE 量化模型的预测准确性。

完整代码

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)


# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)


# define RNN
class SimpleRNN(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(SimpleRNN, self).__init__()
        self.hidden_layer_size = hidden_layer_size
        self.rnn = nn.RNN(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
        predictions = self.linear(rnn_out.view(len(input_seq), -1))
        return predictions[-1]

model = SimpleRNN()
criterion = nn.MSELoss()

optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

# 训练模型
epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')


# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')


# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

利用 LSTM 进行时间序列预测

长短期记忆（LSTM）网络旨在通过更好地管理长期依赖性和异常值来改进递归神经网络（RNN）。然而，LSTM 的真正功效因数据集而异，这凸显了经验验证的必要性。在即将对 "电力生产 "等数据集进行的研究中，我们的目标是对不同算法进行数据驱动的评估，纯粹关注经验结果而非理论预期。以下是为 LSTM 量身定制的 Python 代码示例：

定义LSTM模型

# 定义LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(LSTMModel, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1))
        predictions = self.linear(lstm_out.view(len(input_seq), -1))
        return predictions[-1]

model = LSTMModel()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 180

LSTM完整代码

import torch
import torch.nn as nn
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from statsmodels.tsa.seasonal import seasonal_decompose
from torch.utils.data import DataLoader, TensorDataset


data=pd.read_csv("Electric_Production.csv")
#把data的Date类型转换为datetime类型
data['DATE'] = pd.to_datetime(data['DATE'])
# 设置日期为索引
data.set_index('DATE', inplace=True)
monthly_data = data.IPG2211A2N.resample('ME').mean().reset_index()
monthly_data

# 假设 `monthly_data` 是包含时间序列列 'IPG2211A2N' 的 DataFrame
tmdata = monthly_data['IPG2211A2N'] 
tmdata.plot()

# 导入 seasonal_decompose 函数 参数分别为：
# 时间序列数据，分解模型，周期
from statsmodels.tsa.seasonal import seasonal_decompose
# 
result = seasonal_decompose(tmdata, model='additive', period=12)
result.plot()

# 分解以去除季节性成分
deseasonalized = tmdata - result.seasonal
deseasonalized.plot()

# 对数据进行归一化处理
scaler = MinMaxScaler(feature_range=(-1, 1))
data_normalized = scaler.fit_transform(deseasonalized.values.reshape(-1, 1))
data_normalized

# 将数据转换为序列
def create_sequences(data, seq_length):
    xs, ys = [], []
    for i in range(len(data)-seq_length-1):
        x = data[i:(i+seq_length)]
        y = data[i+seq_length]
        xs.append(x)
        ys.append(y)
    return np.array(xs), np.array(ys)

seq_length = 12
X, y = create_sequences(data_normalized, seq_length)
print(X.shape, y.shape) 
print(X[0:1],'\n', y[0:1])

# 拆分训练集和测试集
X_train, X_test = X[:-3], X[-3-seq_length:-seq_length]
y_train, y_test = y[:-3], y[-3:]
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)


# Convert to PyTorch tensors
X_train = torch.FloatTensor(X_train)
y_train = torch.FloatTensor(y_train).view(-1)
X_test = torch.FloatTensor(X_test)
y_test = torch.FloatTensor(y_test).view(-1)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)



# 定义LSTM模型
class LSTMModel(nn.Module):
    def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
        super(LSTMModel, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_layer_size)
        self.linear = nn.Linear(hidden_layer_size, output_size)
    
    def forward(self, input_seq):
        lstm_out, _ = self.lstm(input_seq.view(len(input_seq), 1, -1))
        predictions = self.linear(lstm_out.view(len(input_seq), -1))
        return predictions[-1]

model = LSTMModel()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
epochs = 180

# # define RNN
# class SimpleRNN(nn.Module):
#     def __init__(self, input_size=1, hidden_layer_size=100, output_size=1):
#         super(SimpleRNN, self).__init__()
#         self.hidden_layer_size = hidden_layer_size
#         self.rnn = nn.RNN(input_size, hidden_layer_size)
#         self.linear = nn.Linear(hidden_layer_size, output_size)
    
#     def forward(self, input_seq):
#         rnn_out, _ = self.rnn(input_seq.view(len(input_seq) ,1, -1))
#         predictions = self.linear(rnn_out.view(len(input_seq), -1))
#         return predictions[-1]

# model = SimpleRNN()
# criterion = nn.MSELoss()

# optimizer = torch.optim.Adam(model.parameters(), lr=0.018)

# # 训练模型
# epochs = 220
for i in range(epochs):
    # 遍历训练集的每个序列和对应的标签
    for seq, labels in zip(X_train, y_train):
        # 重置优化器的梯度
        optimizer.zero_grad()
        # model(seq) 是模型的前向传播，得到模型的输出
        y_pred = model(seq)
        # criterion(y_pred, labels.unsqueeze(-1)) 计算损失，其中 labels.unsqueeze(-1) 是标签的形状
        single_loss = criterion(y_pred, labels.unsqueeze(-1))
        # 反向传播和优化器更新
        single_loss.backward()
        optimizer.step()
    if i % 10 == 0:
        print(f'epoch: {i:3} loss: {single_loss.item():10.8f}')


# model.eval()  # 设置模型为评估模式，关闭 Dropout 和 Batch Normalization 等层的训练模式
# preds_list = []  # 用于存储预测值的列表
model.eval()
preds_list = []
# 遍历测试集，进行预测
with torch.no_grad():
    for i in range(len(X_test)):
        seq = X_test[i].view(-1, 1, 1)  # Reshape to (seq_len, batch_size=1, features=1)
        # model(seq) 前向传播，得到预测值
        pred = model(seq)
        # 将预测值添加到 preds_list 列表中
        preds_list.append(pred.item())
        # 打印预测值和真实值
        print(f'Predicted: {pred.item()}, Actual: {y_test[i].item()}')


# 将预测列表转换为用于反向缩放的 numpy 数组
preds_array = np.array(preds_list).reshape(-1, 1)
preds_inverse = scaler.inverse_transform(preds_array)

# 对实际测试标签进行反变换
y_test_inverse = scaler.inverse_transform(y_test.numpy().reshape(-1, 1))

# 计算 MAPE
mape = np.mean(np.abs((y_test_inverse - preds_inverse) / y_test_inverse)) * 100
print(f'MAPE: {mape}%')

输出如下：

还有类似的方法，就不再演示了，参考的区别如下

数据集：

1\] 电力生产Kaggle 数据集: *https://www.kaggle.com/datasets/shenba/time-series-datasets?select=Electric_Production.csv* Electric_Production.csv \[2\] 洗发水销售Kaggle 数据集: *https://www.kaggle.com/datasets/redwankarimsony/shampoo-saled-dataset* shampoo_sales.csv