一、概述
AdaBoost(Adaptive Boosting,自适应提升)是一种迭代式的集成学习算法,通过不断调整样本权重,提升弱学习器性能,最终集成为一个强学习器。它继承了 Boosting 的基本思想和关键机制,但在具体的实现中有着显著特点,成为具有一定特定性能和适用场景的集成学习算法。
二、算法过程
(1)设置初始样本权重
在算法开始时,为训练数据集中的每一个样本设定一个相同的权重。如对于样本集\(D=\left\{ (x_1,y_1),(x_2,y_2),...,(x_n,y_n) \right\}\),初始权重为\(w^{(1)}=\left( w_{1}^{(1)} ,w_{2}^{(1)},...,w_{n}^{(1)} \right)\) ,其中\(w_{i}^{(1)}=\frac{1}{n}\),即在第一轮训练时,每个样本在模型训练中的重要度是相同的。
(2)训练弱学习器
基于当前的权重分布,训练一个弱学习器。基于当前的权重分布,训练一个弱学习器。弱学习器是指一个性能仅略优于随机猜测的学习算法,例如决策树桩(一种简单的决策树,通常只有一层)。在训练过程中,弱学习器会根据样本的权重来调整学习的重点,更关注那些权重较高的样本。
(3) 计算弱学习器的权重
根据弱学习器在训练集上的分类错误率,计算该弱学习器的权重。错误率越低,说明该弱学习器的性能越好,其权重也就越大;反之,错误率越高的弱学习器权重越小。通常使用的计算公式为
\[\alpha=\frac{1}{2}ln\left( \frac{1-\varepsilon}{\varepsilon} \right) \]
其中\(\varepsilon\)是该弱学习器的错误率。
(4) 更新训练数据的权重分布
根据当前数据的权重和弱学习器的权重,更新训练数据的权重分布。具体的更新规则是,对于被正确分类的样本,降低其权重;对于被错误分类的样本,提高其权重。这样,在下一轮训练中,弱学习器会更加关注那些之前被错误分类的样本,从而有针对性地进行学习。公式为
\[\begin{equation} w_{i}^{(t+1)}=\frac{w_{i}^{(t)}}{Z_t}\cdot \begin{cases} e^{-\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)=y_i \\ e^{\alpha_t}, \hspace{0.5em} if \hspace{0.5em} h_t(x_i)\ne y_i \end{cases} \end{equation} \]
其中,\(w_{i}^{(t)}\)是第\(t\) 轮中第\(i\)个样本的权重,\(Z_t\)是归一化因子,确保更新后的样本权重之和为 1,\(h_t(x_i)\)是第\(t\)个弱学习器对第\(i\)个样本的预测结果。
(5) 重复以上步骤
不断重复训练弱学习器、计算弱学习器权重、更新数据权重分布的过程,直到达到预设的停止条件,如训练的弱学习器数量达到指定的上限,或者集成模型在验证集上的性能不再提升等。
(6)构建集成模型
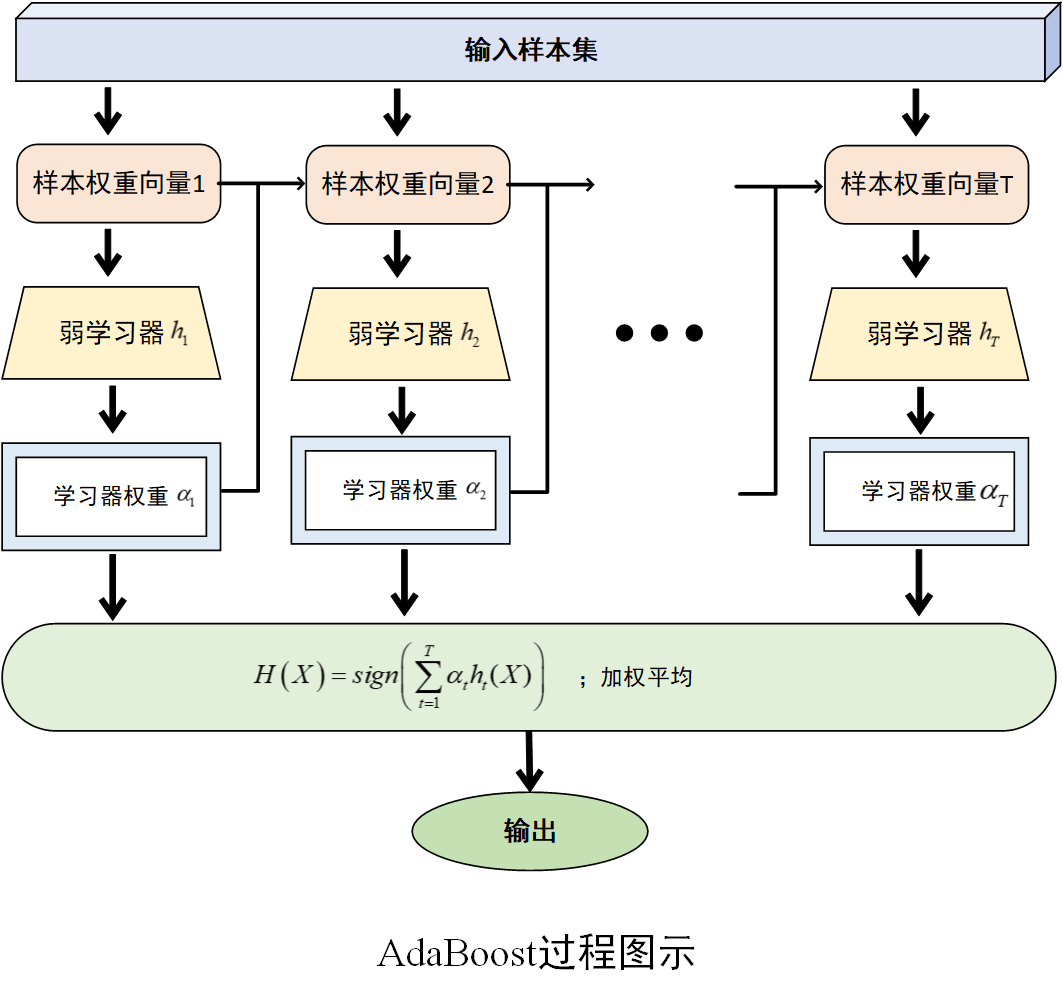
将训练好的所有弱学习器按照其权重进行组合,得到最终的集成模型。如训练得到一系列弱学习器\(h_1,h_2,...,h_T\)及其对应的权重\(\alpha_1,\alpha_2,...,\alpha_T\),最终的强学习器\(H(X)\)通过对这些弱学习器进行加权组合得到。对于分类问题,通常采用符号函数\(H\left( X \right)=sign\left( \sum_{t=1}^{T}{\alpha_th_t(X)} \right)\)输出;对于回归问题,则可采用加权平均的方式输出。
过程图示如下
三、算法特性与应用场景
优势:算法通过不断调整样本权重和组合多个弱学习器,能够有效提高预测的准确性;可以自适应地调整样本的学习重点,对于不同分布的数据集有较好的适应性;对数据的分布没有严格的假设,不需要事先知道关于数据的一些先验知识。
不足:如果训练数据中存在噪声或异常值,可能会过度拟合这些数据,导致在测试集上的泛化能力下降;每次迭代都需要重新计算样本权重和训练弱分类器,当训练数据量较大或迭代次数较多时,计算成本较高。
应用场景:在图像识别、语音识别、目标检测、文本分类、生物信息等方面有着广泛的应用。
四、Python实现
(环境:Python 3.11,scikit-learn 1.6.1)
分类情形
python
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score
# 生成一个二分类的数据集
X, y = make_classification(n_samples=1000, n_features=10,
n_informative=5, n_redundant=0,
random_state=42,n_classes=2)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 创建AdaBoost分类器实例
ada_classifier = AdaBoostClassifier(n_estimators=100, learning_rate=0.1, random_state=42)
# 训练模型
ada_classifier.fit(X_train, y_train)
# 进行预测
y_pred = ada_classifier.predict(X_test)
# 评估模型
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy}")
回归情形
python
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import mean_squared_error
# 生成模拟回归数据
X, y = make_regression(n_samples=1000, n_features=10, n_informative=5, noise=0.5, random_state=42)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建 AdaBoost 回归器
ada_reg = AdaBoostRegressor(n_estimators=100, random_state=42)
# 训练模型
ada_reg.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = ada_reg.predict(X_test)
# 计算均方误差评估模型性能
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差: {mse}")
End.