1. 同态滤波
同态滤波（Homomorphic Filtering）是一种经典的图像增强 方法，主要用于同时校正图像的 非均匀光照 和 增强细节对比度。
同态滤波的核心思想是将图像的光照分量 （低频）和反射分量（高频）分离，并分别进行调整，最终改善图像的对比度和细节。
2. 算法流程
2.1 图像模型
图像可表示为光照分量
和反射分量
的乘积：
其中：
-
：入射光照分量（illumination），通常变化平缓，包含低频信息。
-
：物体的反射分量（reflectance），变化剧烈，包含高频信息（细节、边缘）。
-
：观测到的图像。
2.2 对数变换
为了能够独立处理光照和反射，同态滤波的第一步是对图像的像素值取对数。因为在数学上，乘法运算在取对数后会变成加法运算。
此后，光照分量和反射分量在频域中更易于分离。
2.3 傅里叶变换
对取对数变换后的图像
进行傅里叶变换 ，转换到频域，得到频谱
。
这样做的目的是将图像分解为不同频率的成分。
2.4 设计滤波器
设计一个合适的滤波器函数
，并在频域中将频谱
与该滤波器相乘，得到滤波后的频谱
：
根据频率成分的特性进行增强或衰减。一个典型的同态滤波器会衰减低频成分（减少光照不均），并增强高频成分（增强细节和对比度）。
因此，滤波器函数
的设计是同态滤波的关键，不同的滤波器会产生不同的增强效果。
常见的同态滤波器形式包括：
-
高斯型同态滤波器: 增强高频，衰减低频。过渡平滑，无振铃效应。
-
巴特沃斯型同态滤波器: 具有更平滑的过渡带。阶数可调，灵活性高。
-
指数型同态滤波器: 过渡特性介于高斯和巴特沃斯之间。
-
理想高通同态滤波器: 低频完全抑制，高频完全保留。会导致严重振铃效应，实际应用较少。
这里，我们以高斯型同态滤波器为例，它是一种基于高斯函数设计的频域滤波器，结合同态滤波框架与高斯函数的频域特性，对图像的光照分量（低频）和反射分量（高频）进行差异化调整。我们用以下公式来表示高斯同态滤波器的传递函数：
其中，
-
: 低频增益（通常 <1，抑制光照不均）。
-
: 高频增益（通常 >1，增强细节）。
-
c : 控制滤波器陡峭程度的常数。
-
: 截止频率。
-
：频率点到中心的距离。
这个形式是一种 高斯型高通滤波器，嵌入到同态滤波的增益控制中，用来调节低频（光照分量）和高频（细节分量）的权重。
2.5 傅里叶逆变换
将滤波后的频谱
转换回空间域，得到滤波后的对数图像
：
2.6 指数运算
对图像
的每个像素值进行指数运算，得到最终的增强图像
：
这个步骤是为了恢复原始图像的尺度和亮度范围。由于第一步进行了对数运算，这里需要进行指数运算来还原。
总结一下整个算法的流程
原始图像 → 对数变换 → 傅里叶变换 → 同态滤波 → 逆傅里叶变换 → 指数变换 → 输出图像
3. 使用 OpenCV C++ 实现同态滤波
下面的例子，展示了如何基于上述的算法流程构建单通道同态滤波，以及如何构建高斯型高通同态滤波器。对于彩色图像而言，需要先分离出 B、G、R 通道，每个通道单独使用同态滤波，最后再合并回彩色图像。
go
#include <opencv2/opencv.hpp>
#include <iostream>
usingnamespace cv;
usingnamespacestd;
// 构造高斯型高通同态滤波器
Mat createHighPassFilter(Size size, float gammaH, float gammaL, float c, float D0) {
Mat H(size, CV_32F);
Point center = Point(size.width / 2, size.height / 2);
for (int u = 0; u < size.height; u++) {
for (int v = 0; v < size.width; v++) {
float D = sqrt(pow(u - center.y, 2) + pow(v - center.x, 2));
H.at<float>(u, v) = (gammaH - gammaL) * (1.0f - exp(-c * (D * D) / (D0 * D0))) + gammaL;
}
}
return H;
}
// 单通道同态滤波
Mat homomorphicFilter(const Mat& image, float gammaH, float gammaL, float c, float D0) {
Mat floatImg;
image.convertTo(floatImg, CV_32F); // 转换为 float 类型，方便后续计算
floatImg += 1; // 防止 log(0) 出现无穷大
log(floatImg, floatImg); // 对图像取对数：ln(f(x, y))
// 对图像扩展到最佳 DFT 尺寸
int m = cv::getOptimalDFTSize(image.rows);
int n = cv::getOptimalDFTSize(image.cols);
Mat padded;
copyMakeBorder(floatImg, padded, 0, m - image.rows, 0, n - image.cols, BORDER_CONSTANT, Scalar::all(0));
// 创建复数矩阵，实部为 padded，虚部为 0
Mat planes[] = { padded, Mat::zeros(padded.size(), CV_32F) };
Mat complexI;
merge(planes, 2, complexI);
// 进行傅里叶变换
dft(complexI, complexI);
// 创建高通同态滤波器，尺寸和 padded 一致
Mat H = createHighPassFilter(padded.size(), gammaH, gammaL, c, D0);
// 将频谱从笛卡尔坐标转换为极坐标（幅值和相位）
split(complexI, planes);
Mat mag, phase;
cartToPolar(planes[0], planes[1], mag, phase);
// 在频率域应用滤波器（只对幅值部分）
mag = mag.mul(H);
// 将极坐标转换回笛卡尔坐标
polarToCart(mag, phase, planes[0], planes[1]);
merge(planes, 2, complexI);
// 傅里叶逆变换，回到空域
idft(complexI, complexI);
// 提取实部，去掉填充部分
split(complexI, planes);
Mat realI = planes[0](Rect(0, 0, image.cols, image.rows));
// 归一化到 [0, 10]，避免指数溢出
normalize(realI, realI, 0, 10, NORM_MINMAX);
// 对结果取指数，还原到线性空间
Mat img_out;
exp(realI, img_out);
// 最后归一化到 [0, 255] 并转换为 8 位图像
double minVal, maxVal;
minMaxLoc(img_out, &minVal, &maxVal);
img_out.convertTo(img_out, CV_8U, 255.0 / (maxVal - minVal), -minVal * 255.0 / (maxVal - minVal));
return img_out;
}
int main() {
Mat src = imread(".../landscape.jpg", IMREAD_UNCHANGED);
if (src.empty()) {
cout << "无法加载图像" << endl;
return-1;
}
Mat result;
if (src.channels() == 1) {
// 灰度图像处理
result = homomorphicFilter(src, 1.5f, 0.5f, 1.0f, 30.0f);
} elseif (src.channels() == 3) {
// 彩色图像处理（逐通道）
vector<Mat> channels;
split(src, channels);
vector<Mat> resultChannels(3);
for (int i = 0; i < 3; ++i) {
resultChannels[i] = homomorphicFilter(channels[i], 1.5f, 0.5f, 1.0f, 30.0f);
}
merge(resultChannels, result);
} else {
cout << "不支持的图像通道数" << endl;
return-1;
}
imshow("src", src);
imshow("result", result);
waitKey(0);
return0;
}
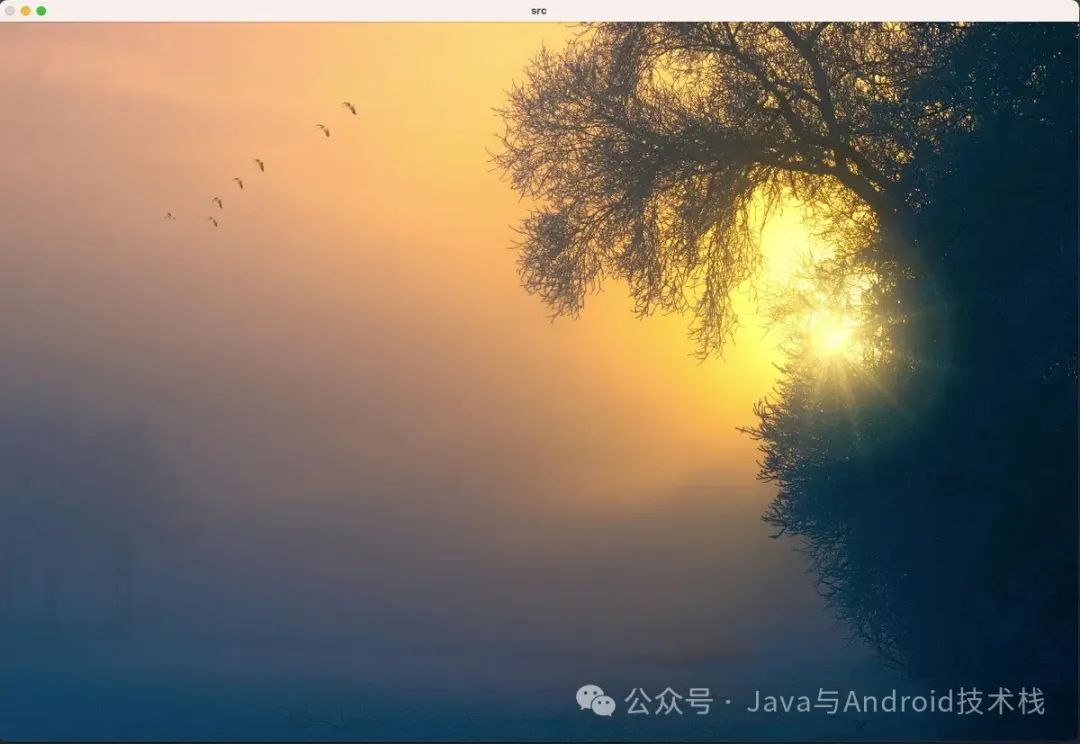原图.png 
同态滤波后的效果图.png
4. 总结
同态滤波是一种通过频域处理解决图像光照不均的关键技术，其作用在于分离并差异化调整图像的低频光照分量和高频反射分量，增强图像对比度和细节，从而提高图像的视觉质量和可分析性。这在光照条件复杂或需要突出局部特征的应用中具有重要意义。