知识点回顾:
- 推断簇含义的2个思路:先选特征和后选特征
- 通过可视化图形借助ai定义簇的含义
- 科研逻辑闭环:通过精度判断特征工程价值
**作业:**参考示例代码对心脏病数据集采取类似操作,并且评估特征工程后模型效果有无提升
python
# 先运行之前预处理好的代码
import pandas as pd
import pandas as pd #用于数据处理和分析,可处理表格数据。
import numpy as np #用于数值计算,提供了高效的数组操作。
import matplotlib.pyplot as plt #用于绘制各种类型的图表
import seaborn as sns #基于matplotlib的高级绘图库,能绘制更美观的统计图形。
import warnings
warnings.filterwarnings("ignore")
# 设置中文字体(解决中文显示问题)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
data = pd.read_csv('heart.csv') #读取数据
data.head() #查看数据的前五行
python
from sklearn.model_selection import train_test_split
X = data.drop(['target'], axis=1) # 特征,axis=1表示按列删除
y = data['target'] # 标签
# # 按照8:2划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 80%训练集,20%测试集
python
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import seaborn as sns
# 标准化数据(聚类前通常需要标准化)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled
python
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
import matplotlib.pyplot as plt
import seaborn as sns
# 评估不同 k 值下的指标
k_range = range(2, 11) # 测试 k 从 2 到 10
inertia_values = []
silhouette_scores = []
ch_scores = []
db_scores = []
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
inertia_values.append(kmeans.inertia_) # 惯性(肘部法则)
silhouette = silhouette_score(X_scaled, kmeans_labels) # 轮廓系数
silhouette_scores.append(silhouette)
ch = calinski_harabasz_score(X_scaled, kmeans_labels) # CH 指数
ch_scores.append(ch)
db = davies_bouldin_score(X_scaled, kmeans_labels) # DB 指数
db_scores.append(db)
print(f"k={k}, 惯性: {kmeans.inertia_:.2f}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")
# 绘制评估指标图
plt.figure(figsize=(15, 10))
# 肘部法则图(Inertia)
plt.subplot(2, 2, 1)
plt.plot(k_range, inertia_values, marker='o')
plt.title('肘部法则确定最优聚类数 k(惯性,越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('惯性')
plt.grid(True)
# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)
# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)
# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k(越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)
plt.tight_layout()
plt.show()
python
k=2, 惯性: 3331.64, 轮廓系数: 0.166, CH 指数: 54.87, DB 指数: 2.209
k=3, 惯性: 3087.69, 轮廓系数: 0.112, CH 指数: 41.36, DB 指数: 2.544
k=4, 惯性: 2892.52, 轮廓系数: 0.118, CH 指数: 36.06, DB 指数: 2.175
k=5, 惯性: 2814.65, 轮廓系数: 0.094, CH 指数: 29.76, DB 指数: 2.386
k=6, 惯性: 2673.22, 轮廓系数: 0.095, CH 指数: 28.13, DB 指数: 2.377
k=7, 惯性: 2596.68, 轮廓系数: 0.088, CH 指数: 25.50, DB 指数: 2.290
k=8, 惯性: 2464.39, 轮廓系数: 0.115, CH 指数: 25.22, DB 指数: 2.136
k=9, 惯性: 2415.63, 轮廓系数: 0.105, CH 指数: 23.18, DB 指数: 2.133
k=10, 惯性: 2337.41, 轮廓系数: 0.111, CH 指数: 22.31, DB 指数: 2.056
python
# 提示用户选择 k 值
selected_k = 4# 这里可以根据评估结果选择合适的 k 值
# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k, random_state=42)
kmeans_labels = kmeans.fit_predict(X_scaled)
X['KMeans_Cluster'] = kmeans_labels
# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()
# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(X[['KMeans_Cluster']].value_counts())
python
X.columns
python
Index(['age', 'sex', 'cp', 'trestbps', 'chol', 'fbs', 'restecg', 'thalach',
'exang', 'oldpeak', 'slope', 'ca', 'thal', 'KMeans_Cluster'],
dtype='object')
python
x1= X.drop('KMeans_Cluster',axis=1) # 删除聚类标签列
y1 = X['KMeans_Cluster']
# 构建随机森林,用shap重要性来筛选重要性
import shap
import numpy as np
from sklearn.ensemble import RandomForestClassifier # 随机森林分类器
model = RandomForestClassifier(n_estimators=100, random_state=42) # 随机森林模型
model.fit(x1, y1) # 训练模型,此时无需在意准确率 直接全部数据用来训练了
python
shap.initjs()
# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(x1) # 这个计算耗时
shap_values.shape # 第一维是样本数,第二维是特征数,第三维是类别数
# --- SHAP 特征重要性条形图 (Summary Plot - Bar) ---
print("--- 1. SHAP 特征重要性条形图 ---")
shap.summary_plot(shap_values[:, :, 0], x1, plot_type="bar",show=False) # 这里的show=False表示不直接显示图形,这样可以继续用plt来修改元素,不然就直接输出了
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()
python
# 此时判断一下这几个特征是离散型还是连续型
import pandas as pd
selected_features = ['sex', 'age',
'thalach', 'slope']
for feature in selected_features:
unique_count = X[feature].nunique() # 唯一值指的是在某一列或某个特征中,不重复出现的值
# 连续型变量通常有很多唯一值,而离散型变量的唯一值较少
print(f'{feature} 的唯一值数量: {unique_count}')
if unique_count < 10: # 这里 10 是一个经验阈值,可以根据实际情况调整
print(f'{feature} 可能是离散型变量')
else:
print(f'{feature} 可能是连续型变量')
python
sex 的唯一值数量: 2
sex 可能是离散型变量
age 的唯一值数量: 41
age 可能是连续型变量
thalach 的唯一值数量: 91
thalach 可能是连续型变量
slope 的唯一值数量: 3
slope 可能是离散型变量
python
import matplotlib.pyplot as plt
# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()
for i, feature in enumerate(selected_features):
axes[i].hist(X[feature], bins=20)
axes[i].set_title(f'Histogram of {feature}')
axes[i].set_xlabel(feature)
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
python
# 绘制出每个簇对应的这四个特征的分布图
X[['KMeans_Cluster']].value_counts()
# 分别筛选出每个簇的数据
X_cluster0 = X[X['KMeans_Cluster'] == 0]
X_cluster1 = X[X['KMeans_Cluster'] == 1]
X_cluster2 = X[X['KMeans_Cluster'] == 2]
python
# 先绘制簇0的分布图
import matplotlib.pyplot as plt
# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()
for i, feature in enumerate(selected_features):
axes[i].hist(X_cluster0[feature], bins=20)
axes[i].set_title(f'Histogram of {feature}')
axes[i].set_xlabel(feature)
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
python
# 先绘制簇1的分布图
import matplotlib.pyplot as plt
# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()
for i, feature in enumerate(selected_features):
axes[i].hist(X_cluster1[feature], bins=20)
axes[i].set_title(f'Histogram of {feature}')
axes[i].set_xlabel(feature)
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()
python
# 先绘制簇2的分布图
import matplotlib.pyplot as plt
# 总样本中的前四个重要性的特征分布图
fig, axes = plt.subplots(2, 2, figsize=(12, 8))
axes = axes.flatten()
for i, feature in enumerate(selected_features):
axes[i].hist(X_cluster2[feature], bins=20)
axes[i].set_title(f'Histogram of {feature}')
axes[i].set_xlabel(feature)
axes[i].set_ylabel('Frequency')
plt.tight_layout()
plt.show()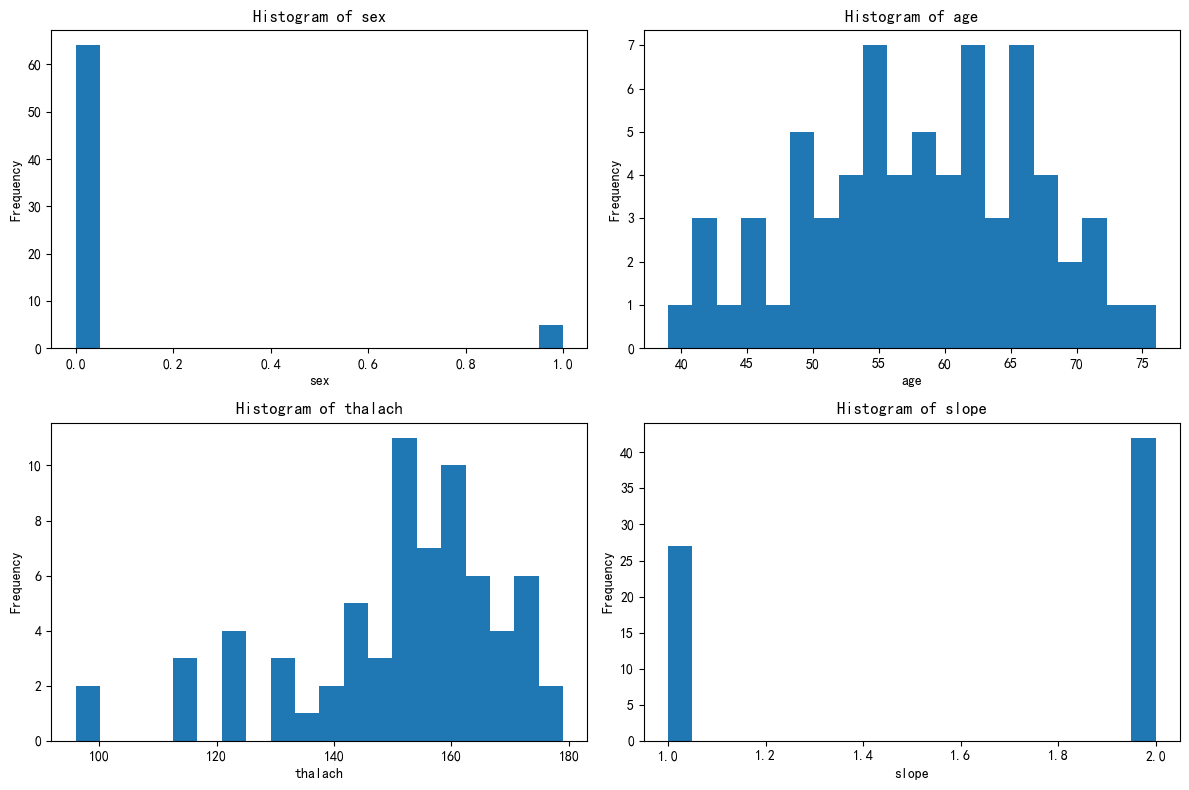
把这三个簇的图发给ai,让ai给你定义
Cluster 0
-
性别(sex):几乎全为1,说明该簇基本上全是男性。
-
年龄(age):集中在40--55岁之间,中年群体为主。
-
最大心率(thalach):主要集中在160--180之间,心率偏高。
-
斜率(slope):绝大多数为2(即 ST 段的下降趋势),这通常和心脏负荷能力减弱有关。
定义建议 :
中年男性高心率群体,可能代表存在明显心脏应激反应的亚群,需重点关注潜在心血管风险。
Cluster 1
-
性别(sex):男女比例相对较均衡,但仍以男性为主。
-
年龄(age):多集中在55--65岁之间,比 cluster 0 年长。
-
最大心率(thalach):显著低于 cluster 0,主要在100--140之间。
-
斜率(slope):绝大多数为1,表示 ST 段保持水平,为中性或轻度异常。
定义建议 :
老年中低心率群体,可能反映一种较稳定但功能性心脏下降的群体,潜在慢性病风险较高。
Cluster 2
-
性别(sex):几乎全为女性(sex = 0)。
-
年龄(age):主要在55--70岁,略偏老年。
-
最大心率(thalach):分布中等偏高(140--170),高于 cluster 1,低于 cluster 0。
-
斜率(slope):1 和 2 比例较均衡,部分存在 ST 段下降。
定义建议 :
老年女性中等心率群体,可能为具有一定心脏代偿能力但仍需随访的女性心血管亚群。
总结比较表:
| 特征 | Cluster 0 | Cluster 1 | Cluster 2 |
|---|---|---|---|
| 性别 | 几乎全为男性 | 多为男性 | 几乎全为女性 |
| 年龄 | 40--55岁 | 55--65岁 | 55--70岁 |
| 最大心率 | 160--180(较高) | 100--140(较低) | 140--170(中等) |
| ST斜率 | 大多为下降(2) | 多为水平(1) | 1和2均有 |