游戏引擎学习第273天:动画预览

回顾并为一天的内容定下基调

。目前我们正在编写角色的移动代码，实际上，我们已经在昨天完成了一个简单的角色跳跃的例子。所以今天的重点是，开始更广泛地讨论动画，因为我们希望对现有的动画进行调整，让它看起来更加令人满意。

目前角色的动画效果还比较简单，只是一个小角色在地面上跳跃。跳跃的动作虽然完成，但看起来很机械化，没有太多的细节和吸引力。角色的动作只是一个简单的抛物线跳跃，头部和身体的连接也没有表现出足够的连贯性，感觉像是两个部分分离了，而没有更自然的动画效果。因此，下一步的目标是使角色的动画更加生动和真实。

为了实现这个目标，我们需要对动画进行更多的调节和细化。头部和身体应该保持连接，并且在角色跳跃时，身体应当随着跳跃的弧线伸展，这样才能看起来更加自然。另外，现有的跳跃动画在运动过程中没有足够的细腻感，缺乏一些微妙的细节调整，因此，后续的工作将会专注于如何让动画看起来更流畅、更具生命力，而不仅仅是让角色简单地跳跃。

接下来，我们会深入讨论一些动画的基础知识，以帮助那些对动画了解不多的人更好地理解我们将要做的事情。这样做的目的是为了解决动画中的实际问题，并且从一个更高的层面来理解如何通过编程来改善和优化游戏中的角色动画。

我们将讨论动画的基本原理，尤其是在游戏开发中的应用。为了帮助大家更好地理解这些问题，我们会在黑板上做一些讲解，介绍一些重要的动画概念。这个过程可能需要一定时间，取决于我们深入讨论的程度。我们希望通过这些讨论，让大家能够清晰地理解如何从技术角度处理动画问题，并且理解每个动画调整背后的逻辑和思路。

黑板：动画

在讨论动画时，我们首先需要明确我们所说的"动画"到底是什么意思。显然，我们从一个非常基础的前提出发，特别是当涉及到计算机动画和游戏中的动画时。我们可以把动画想象成一条电影胶片，在这条胶片上，我们有多个帧：第0帧、第1帧、第2帧、第3帧等。我们可以画出这些帧之间的 perforations（孔洞），以模拟电影胶片的样子。

实际上，我们并没有显示所谓的"动画"，我们展示的仅仅是静态帧，而这些静态帧是希望观众看起来像是在显示动画、像是在展示运动。通常，我们的目标是让这些静止的画面看起来像是一个运动的过程，类似于我们拍摄电影或电视节目时的效果。原因是人们已经习惯于通过显示器观看电影或电视节目，这种模式也被广泛应用到游戏当中。

为了让这些静态帧看起来像是运动的，我们的任务是捕捉到运动的效果。假设我们正在模拟一个摄像机的过程，摄像机内部的胶片（即负片）正在不断流动。当胶片流动时，它会经过胶片卷轴，捕捉场景中的每一个瞬间。这个捕捉的过程是根据摄像机的设置来决定的，具体来说，摄像机内部有一个装置叫做"快门"或"光圈"，它的作用是决定在每一帧捕捉过程中，光线进入的量和时间。

每个人都看过摄像机的快门，它通常看起来像是一个旋转的物体，会从一个小的形状展开，逐渐变大，最终又收回。这个快门的大小和打开的时长决定了每一帧图像的曝光时间，也就是说，决定了每一帧能捕捉到多少信息。快门越大，曝光时间越长，进入的光线就越多，画面就越亮。相反，快门越小，曝光时间越短，画面就越暗。

我们不需要深入探讨快门的具体机制，但可以理解的是，快门的操作对动画效果有着非常大的影响，它决定了画面捕捉的精细程度。每一帧的拍摄，实际上都是对运动过程的一个截取，而这些帧按顺序播放，就给我们呈现出"动画"的效果。因此，在制作计算机动画时，我们的目标就是尽可能精确地模拟这种通过一系列静止帧来展示运动的过程。

黑板：曝光时间和时间间隔

在讨论动画时，特别是在计算机动画和游戏中的动画，我们需要理解一些基本概念，比如曝光时间和它对动画效果的影响。首先，曝光时间是指在拍摄过程中，摄像机的快门打开的时间，决定了光线进入的时间。这个时间段内，光子进入摄像机并照射到胶片上，从而曝光胶片。

对于动画来说，每一帧并不是一个瞬间，而是一个时间间隔。在动画中，我们并不关心物体在某一时刻的瞬间位置，而是关心物体在某个时间间隔内的移动。这个时间间隔与摄像机的曝光时间密切相关。当摄像机的快门打开时，光线进入并曝光胶片，直到快门关闭。通过控制快门速度，我们可以决定曝光的时间长度。比如，如果快门速度设置为1/60秒，那么每帧的曝光时间大约是16.6毫秒。曝光的时间越长，进入的光子数量就越多。

从更广泛的角度来看，计算机图形学中的动画实际上是在捕捉时间间隔内发生的运动。我们并不只是绘制单独的一帧图像，而是模拟一个物体在一段时间内的移动轨迹。这个时间间隔是我们所要模拟的内容，而不是仅仅捕捉瞬时位置。如果未来的计算能力达到极致，可能我们可以完美地模拟这种时间间隔内的运动，捕捉每个细节。

在现实中，尤其是在电影拍摄中，快门速度和曝光时间会产生运动模糊效果，这也是电影画面的一部分。如果一个物体在屏幕上快速移动，快门开启的时间段内，物体的多个位置会被捕捉到，从而产生模糊效果，观众的眼睛会看到一条流畅的运动轨迹，这种模糊传递了运动的感觉，使得画面显得更生动、更丰富。

然而，在计算机图形中，由于计算能力的限制，模拟这种运动模糊并不是那么容易。虽然可以通过一些近似方法来模拟运动模糊，但这些方法并不完美，通常会在一些地方做出妥协。很多时候，我们只能通过提高帧率来弥补运动模糊的不足，例如通过增加到60帧每秒，尽量减少因帧率过低而产生的不自然感觉。然而，即使如此，没有运动模糊的计算机图形效果与实际电影画面也会有所不同，尤其是在快速运动的场景中，比如快速行驶的汽车或飞驰的子弹等，这些快速运动的物体在没有运动模糊的情况下，画面会显得更加锐利和清晰。

理解这些概念对于制作更自然、流畅的动画非常重要，因为动画的真实感不仅仅依赖于单帧图像的绘制，还需要考虑时间间隔的表现，以及如何通过模拟自然的运动来提升动画的质量。

摄像机拍摄运动时的模糊效果和轨迹的底层物理原因可以追溯到光、传感器工作原理以及物体运动的交互。以下从物理角度详细解析：

1. 运动模糊的物理原因

光的传播与传感器曝光 ：
- 光子以恒定速度（约3×10⁸ m/s）传播，携带物体信息到达摄像机镜头。传感器通过光电效应将光子转化为电信号，记录图像。
- 曝光期间，传感器累积接收到的光子，形成图像。曝光时间（快门时间）决定了传感器累积光子的时间窗口。
物体运动的影响 ：
- 当物体在曝光时间内移动，其反射或发出的光子在传感器上的投影位置会发生变化。例如，一个移动的物体在时间 t 0 t_0 t0 到 t 1 t_1 t1 内从位置 A A A 移动到 B B B，其光子会在传感器上形成从 A ′ A' A′ 到 B ′ B' B′ 的连续投影。
- 传感器无法区分这些光子来自物体的不同位置，因此将所有光子信号叠加，表现为模糊。模糊的程度与物体在曝光时间内移动的距离成正比，数学上可表示为：
  模糊长度 ≈ v ⋅ t \text{模糊长度} \approx v \cdot t 模糊长度≈v⋅t
  其中 v v v 是物体在画面中的相对速度， t t t 是曝光时间。
光子统计与噪声 ：
- 在短曝光时间下，光子数量较少，信号可能受到光子散粒噪声（shot noise）的影响，导致图像细节丢失。在长曝光时间下，光子叠加导致运动模糊覆盖细节。

2. 轨迹效果的物理原因

长曝光与光子路径积分 ：
- 轨迹是运动模糊的极端情况，发生在曝光时间较长时。物体在曝光时间内移动的距离足够大，传感器记录的光子形成连续的路径。
- 物理上，传感器记录的是光子在时间 t t t 内的强度积分。对于一个明亮的移动物体（如车灯），其光子在传感器上形成高强度的连续轨迹，表现为光迹。
- 数学描述：假设物体以速度 v v v 移动，其光强为 I ( t ) I(t) I(t)，传感器记录的图像强度为：
  I image ( x ) = ∫ t 0 t 1 I ( t ) ⋅ δ ( x − v t ) d t I_{\text{image}}(x) = \int_{t_0}^{t_1} I(t) \cdot \delta(x - vt) \, dt Iimage(x)=∫t0t1I(t)⋅δ(x−vt)dt
  其中 δ \delta δ 表示光子在传感器上的投影位置，积分结果形成轨迹。
点扩散函数（PSF） ：
- 运动模糊和轨迹可以看作是点扩散函数（PSF）作用的结果。PSF描述了点光源在成像系统中的扩散形状。对于运动物体，PSF不再是点状，而是沿运动方向拉伸的线状，导致轨迹或模糊。

3. 滚转快门效应的物理原因

CMOS传感器逐行扫描 ：
- 许多摄像机使用CMOS传感器，采用滚转快门（rolling shutter）方式。传感器逐行曝光，从画面顶部到底部依次读取光电信号。
- 曝光时间差：假设传感器每行曝光时间为 Δ t \Delta t Δt，画面高度为 H H H，则画面底部比顶部晚 H ⋅ Δ t H \cdot \Delta t H⋅Δt 开始曝光。对于快速移动的物体，不同行捕捉到的物体位置不同，导致图像扭曲或轨迹状效果。
- 物理机制：物体在时间 t t t 内的位移 Δ x = v ⋅ t \Delta x = v \cdot t Δx=v⋅t 导致每行记录的物体位置偏移，表现为斜向轨迹或形变。
数学描述 ：
- 假设物体沿 x x x 轴以速度 v v v 移动，传感器行扫描速度为 s s s，则第 y y y 行的物体位置偏移为：
  x ( y ) = v ⋅ y s x(y) = v \cdot \frac{y}{s} x(y)=v⋅sy
  这种偏移在快速运动时形成明显的轨迹或扭曲。

4. 光学与镜头的影响

镜头焦距与视角 ：
- 焦距影响物体在传感器上的投影速度。长焦距镜头放大物体运动，导致相同的物理速度 v v v 在画面中表现为更大的位移，模糊或轨迹更明显。
- 数学上，画面中的速度 v image v_{\text{image}} vimage 与焦距 f f f 成正比：
  v image ∝ v ⋅ f d v_{\text{image}} \propto \frac{v \cdot f}{d} vimage∝dv⋅f
  其中 d d d 是物体到镜头的距离。
光圈与光量 ：
- 光圈大小（f值）影响进光量，间接影响快门速度选择。在低光环境下，需更长的曝光时间以收集足够光子，从而加剧模糊或轨迹。

5. 总结

运动模糊：光子在曝光时间内因物体运动而在传感器上形成连续投影，导致图像细节叠加丢失。
轨迹：长曝光下，光子路径积分形成连续光迹，表现为明亮轨迹。
滚转快门：CMOS传感器逐行曝光导致时间差，快速运动物体在不同行产生位置偏移，形成轨迹或扭曲。
光学因素：焦距、光圈等影响运动在画面中的表现。

黑板：瞬时动画

在游戏开发中，尤其是在处理角色动画时，我们通常会简化问题，专注于即时（瞬间）的问题。在这种情况下，我们假设帧率足够高，以至于我们不需要过多担心运动模糊，或者在某些情况下会将运动模糊作为"修补"效果加进去。比如，假设一个角色挥动剑时，剑的轨迹可能会有一些模糊效果，我们可以通过"黑客"手段来实现，但我们并不会尝试为所有的动画都做出完美的运动模糊处理。

1. 瞬间动画和"黑客"解决方案

当我们处理瞬间动画时，实际上是在模拟一个无穷快的快门，假设它能在极短的时间内迅速开启和关闭。在现实中，这是不可能做到的，因为没有足够的光子能在瞬间通过镜头并曝光到胶片上。因此，真实世界并没有类似于我们所说的"瞬间"的动画效果。尽管如此，在游戏开发中，我们可以采用一些"黑客"方式来解决这个问题，尤其是在需要快速、流畅的运动表现时。比如，快速移动的物体和角色可能不需要过多的运动模糊，游戏帧率足够高时，视觉效果往往不会受到太大影响。

2. 游戏中的动画采样

游戏中的动画处理通常依赖于采样，即在某个特定时刻（例如每一帧）获取世界的状态。在技术上，我们通过时间步长来推进动画的进程。例如，假设我们在时间点 T0 时获取物体的位置，并在下一帧的 T1 进行更新，时间步长通常是每秒 60 帧（1/60 秒）。这种方法让我们能够精确地控制每一帧的状态，从而确保角色的动画流畅运行。

更进一步，现代游戏不再限制于固定的帧率（如 60 帧），而是可以动态适应硬件的性能。例如，某些设备的帧率可能为 30 帧，或低于 60 帧，但为了保证游戏的可玩性，仍然可以保持流畅的表现。

3. 灵活的时间步长

为了让动画系统更加灵活，游戏开发通常会采用浮动时间步长的方式。这意味着我们不再固定每一帧的时间步长，而是可以根据实际的帧率动态调整时间步长。例如，若帧率较低（如 30 帧/秒），我们可能会调整每次更新的时间步长为更长时间。而在帧率较高的情况下，时间步长会变得更短，从而保证动画的流畅性。

这种方法的关键在于灵活性，允许开发者根据不同硬件性能进行调整，而不仅仅是依赖固定的帧率。理想情况下，游戏引擎应能支持任意的时间步长采样，例如，我们可以每次以 1/120 秒或 1/125 秒为单位进行时间更新。

4. 动画函数的设计

在游戏中，我们通常会将世界的状态视为一个函数，具体来说是关于时间的函数。每次更新时，我们会通过时间步长来调整状态。这个函数通常是由多个子函数组成的，每个子函数负责处理不同的动画或物体的状态。例如，一个函数可能负责更新角色的位置，另一个函数可能负责更新角色的头部运动。

游戏中的动画函数分为两种类型：

显式函数（Explicit Functions）：这些函数可以直接输出物体在某个时间点的位置，通常用于描述那些随时间变化的复杂动画，如角色跳跃的路径。
增量更新函数（Incremental Update Functions）：这类函数通常接受当前的位置和变化量（增量），然后根据这些信息计算下一个时间点的位置。例如，角色的移动可能是通过这种方式来更新的。

5. 基于时间的动画更新

在游戏引擎中，通常通过一个核心函数（例如 game_update 或 render）来更新世界状态。这个更新过程是递归的，基于每个时间步长进行迭代。在实际应用中，游戏世界的状态通常由多个小的函数组成，每个函数处理不同的物理或动画效果。通过这些函数的组合，我们能够模拟出游戏中的角色动作、物体移动等一系列效果。

综上所述，现代游戏中的动画通常依赖于灵活的时间步长采样和多函数的组合更新。尽管现实中的动画存在一些不可避免的物理限制，例如运动模糊，但在游戏中，我们可以通过合理的设计和技术手段弥补这些限制，实现流畅的角色和物体动画效果。

黑板：使用欧拉步长进行数值积分以计算瞬时动画

在游戏开发中，处理角色和物体的动画时，我们通常会使用两种类型的函数来计算位置和运动。

1. 显式函数与增量更新

显式函数：这种函数能够直接根据时间输出物体的精确位置。例如，角色的跳跃动画可以通过显式函数来精确计算，因为跳跃从开始到结束有明确的路径和时间，直接给出物体在每个时刻的位置。
增量更新函数：这类函数要求输入物体的前一个位置，并计算出当前位置。基本上，这类函数依赖于物体在某一时刻的"速度"或"加速度"信息，并通过数值积分的方式来更新位置。也就是说，它会计算物体当前速度的变化（即函数的导数），然后乘以时间步长，从而得出新的位置。

2. 数值积分：前向欧拉法

增量更新通常采用一种叫做"前向欧拉法"（Forward Euler）的方法。这种方法的核心思想是：我们知道物体当前位置和速度（即位置的导数），然后将速度乘以时间步长，从而更新物体的位置。这个过程相当于通过当前的状态（位置和速度）来预测下一时刻的位置。

公式：

New Position = Old Position + Velocity × Time Step \text{New Position} = \text{Old Position} + \text{Velocity} \times \text{Time Step} New Position=Old Position+Velocity×Time Step

这种方法是数值积分中的一种简单方式，但它并不十分精确，因为它忽略了速度和加速度的变化。然而，尽管这种方法很基础，它在大多数游戏中的应用并不会遇到太大问题，特别是在物理模拟比较简单的情况下。

3. 前向欧拉法的局限

前向欧拉法虽然简单且高效，但其准确性较差，尤其是在涉及复杂的物理模拟时。因为物体的速度和加速度是不断变化的，而欧拉法将这种变化忽略，导致在计算物体的下一位置时出现误差。

但对于许多游戏场景而言，这种误差并不明显，特别是在物理行为不复杂时。比如，大多数角色运动、简单的物体碰撞和跳跃等都能通过前向欧拉法来很好地模拟。而且，即便物理模型不完全准确，只要误差足够小，就能保持游戏的流畅性和可玩性。

4. 复杂动画的挑战

对于复杂的动画，像角色的跳跃、奔跑等，我们通常无法用简单的增量更新函数来表示物体的路径。跳跃的轨迹通常是一个精确的曲线，直接使用显式函数就能得到精确的轨迹，而不需要每一帧都进行增量计算。但对于一些实时计算的动画，像角色与环境的交互，涉及到多种力的作用（比如碰撞、重力等），这些物理过程是动态变化的，无法用一个简单的函数来表达，因此需要进行数值更新。

5. 实际应用中的问题

在实际游戏中，很多时候我们必须根据物体与环境的相互作用进行频繁的计算和更新，这使得我们无法直接使用显式的数学公式来描述角色或物体的所有运动轨迹。尤其是在角色与环境的互动中，物体的加速度和速度常常会发生剧烈变化（如突然跳跃、撞击等），因此我们需要使用数值方法来进行逐步的更新，而这些方法常常是近似的。

然而，即便如此，使用显式函数（如跳跃的轨迹函数）来精确描述某些特定动作仍然是非常理想的，它能带来非常高效且准确的动画效果。例如，当角色跳跃时，如果我们能事先计算好跳跃的路径，就不需要在每一帧都进行复杂的计算。

6. 总结

总结来说，游戏中的动画通常由两类函数组成：显式函数和增量更新函数。显式函数能精确计算物体在特定时刻的位置，而增量更新函数依赖于物体的当前状态（如位置、速度等），并通过数值积分方法更新位置。尽管前向欧拉法简单且高效，但它在处理复杂的物理和动画时并不总是精确，因此我们需要在实际开发中平衡精度与性能。对于简单的动画，显式函数非常有用，而对于更复杂的物理行为和动态交互，增量更新和数值方法则是更常见的选择。

黑板：许多关于时间 t 的函数

在处理游戏中的动画时，我们通常会遇到很多不同的时间变量（T）。这些时间变量代表了不同的动画部分，例如角色头部的上下摆动（head bobbing）或跳跃（hop），每个动画都有其自己的时间值。这些不同的时间变量通常会有不同的时间范围，它们分别控制着每个动画的变化过程。

1. 时间变量与动画

在理论上，我们可能会希望有一个统一的函数 F(T)，该函数接受时间 T 作为输入，输出整个世界的状态，包括所有角色和物体的精确位置。但实际上，这个理想化的函数并不存在。取而代之的是，游戏中通常会有多个不同的子函数，这些子函数分别对应不同的动画和动作，它们各自有各自的时间变量（如跳跃动画的 T_hop、头部摆动的 T_bob 等）。

2. 时间的传递与更新

在动画计算中，通常会使用一个"增量时间" (delta T) 来更新每一帧的状态。增量时间是当前帧与上一帧之间的时间差。我们用这个增量时间来更新所有动画中的时间变量。例如，在跳跃动画中，我们会将 delta T 加到当前的跳跃时间 T_hop 上，从而得到新的跳跃位置。

这种增量时间的处理方法会被广泛应用于游戏中的所有动画计算。无论是通过直接的时间更新（如在显式函数中计算位置），还是通过数值方法（如欧拉法）进行位置更新，delta T 都是核心驱动因素。

3. 欧拉法与数值更新

有些情况下，更新过程并不是直接通过计算位置来获得结果，而是通过类似欧拉法的数值步骤进行更新。在这种情况下，物体的当前位置是通过已知的速度和加速度计算的，而不是通过精确的数学公式得出的。即便如此，这种欧拉步进方法依然是有效的，尤其是在物理行为较为简单的情况下。

欧拉法的更新方式一般包括：

保存当前的位置。
计算物体的速度或加速度（如果有）。
通过乘以增量时间更新位置，即：

New Position = Old Position + Velocity × Delta T \text{New Position} = \text{Old Position} + \text{Velocity} \times \text{Delta T} New Position=Old Position+Velocity×Delta T

这种方法简单而高效，但它并不精确，尤其是在物理行为复杂时。对于大多数游戏来说，这种简单的数值更新是足够的，尤其是当物理行为并不涉及复杂的变化时。

4. 动画的分离与组合

虽然我们理想中可能希望有一个能一次性计算出所有物体位置的函数，但现实中我们通常会将不同的动画过程拆分成多个子函数，每个子函数负责更新某个特定的动画。每个动画部分都有自己的时间变量，所有这些子函数最终会在每一帧更新后，汇总出整个游戏世界的状态。

这些子函数可以是直接计算位置的显式函数（如跳跃轨迹的计算），也可以是通过增量更新的方式来进行物体位置更新（如使用欧拉法的物理更新）。

5. 总结

在实际的游戏开发中，动画的更新通常并不是通过一个单一的函数来实现的，而是通过多个函数和时间变量的组合。每个动画部分都有其独立的时间变量，这些时间变量在每一帧都会被更新，并且通过增量时间 delta T 驱动所有动画的进展。无论是通过显式函数还是数值积分方法，增量时间都是更新过程中的关键因素。通过这种方式，游戏能够实现复杂的动画效果，同时保持良好的性能和可玩性。

黑板：物理学与动画

在游戏开发中，通常会把根据时间来评估物体状态的过程分为两类：动画和物理。虽然这两者看似不同，但它们本质上都是对物体进行"动画化"或"物理模拟"。当我们有一个随时间变化的函数，这个函数能够给定某个时间 T 来输出物体的状态时，这个过程就被称为"动画"。例如，角色的动作、跳跃、走路等都可以通过这种方法来表示。

另一方面，当我们处理物体的运动，并根据某些规则（如速度、加速度、碰撞等）来推算物体的最终位置时，这个过程就叫做"物理"。这里我们通过给定增量时间（delta T）来计算物体的位置和速度变化。这种方式通常用来模拟更为真实的物理运动。

尽管在语义上动画和物理有所不同，但在高层次的统一概念下，它们可以看作是同一个过程。无论是动画还是物理，本质上都是在通过时间的推移，按照一定的规则来更新物体的位置和状态。因此，在代码实现中，这两者往往被认为是相似的，都是通过时间推移来控制物体运动的过程。

动画通常涉及到通过插值或关键帧来控制角色或物体的运动，这种方法由艺术家预先设计好，游戏引擎根据这些设计来计算角色的状态。
物理则通常是通过数值计算来模拟物体的运动，物体的位置和速度是通过物理引擎动态计算出来的，这些运动通常受真实物理规律的约束。

尽管两者看起来不同，但它们的核心目的都是让物体按照一定规则随时间变化，并在游戏世界中呈现出合理的动态效果。因此，动画和物理常常可以互相转换或融合，只是在不同的上下文中，我们更倾向于使用不同的术语来区分它们。

黑板：动画技术：B样条和欧拉角

在动画中，提到"F(T)"的概念时，实际上是在讨论通过时间来描述物体状态变化的函数。这种动画函数通常用来控制物体或角色在一段时间内如何变化。为了实现这一目标，常用的技术之一就是B样条（B-Splines）。B样条被广泛应用于动画制作中，尤其是在需要平滑过渡的情况下。

B样条的基本思想是通过一组控制点（也叫"句柄"）来定义曲线，这些控制点帮助我们创建平滑的路径。当我们在时间上给定一个T值时，物体就会沿着B样条曲线移动。具体来说，如果我们想让某个物体沿着一个特定的曲线或路径运动，通常会通过B样条来描述这个路径，然后根据时间T的变化来控制物体沿路径运动的过程。

例如，在角色的动画中，如果需要控制某个关节的旋转，可以使用B样条来控制这个关节的角度变化。类似地，B样条不仅用于位置的变化，也可以用来描述物体的旋转（如欧拉角）或其他属性的变化。通过B样条可以实现平滑的旋转过渡，使得角色的运动更为自然和流畅。

B样条的阶数决定了它的复杂度和形状：

零阶B样条：就是简单的点，表示静止不动的物体。
一阶B样条：表示一条直线，即物体以恒定的速度直线运动。
二阶B样条：表示一条抛物线，这种曲线通常用于物体的加速或减速运动。
三阶B样条：表示立方曲线，这种曲线可以更加灵活地控制物体的运动，通常用于复杂的动画。

B样条作为动画中的常用工具，其主要优势在于它们能提供平滑的过渡效果，使得物体或角色的运动看起来更自然，避免了明显的跳跃或不连贯的变化。在实际应用中，B样条曲线不仅用于角色的位移控制，还广泛应用于关节旋转、摄像机运动、路径跟踪等多种场景，成为动画系统中的重要组成部分。

黑板：B样条的阶数

我们现在讨论的是 B 样条（B-spline）曲线，它是一种在动画制作中被广泛使用的工具。在所有常见的动画软件中，B 样条几乎无处不在。它根据不同的阶数，表现出不同的曲线特性，用来控制动画中物体随时间 T 的状态变化。下面是对不同阶数 B 样条的详细说明和它们在动画中的意义：

1. 0阶 B 样条（Step Function）

0阶 B 样条表现为阶跃函数，意味着动画中没有平滑过渡，状态是"瞬间跳跃"的。

表现形式是"瞬移"。
在某一时间点，角色或物体在一个位置；一旦时间跨过某个阈值，它就"立刻"跳到另一个位置。
这类动画通常用于控制某些突变动作，如开关切换、状态翻转等。

2. 1阶 B 样条（线性插值）

1阶 B 样条即线性插值（Linear Interpolation, 简称 Lerp），是最基础的平滑过渡方式。

表现为直线，从一个关键帧平滑过渡到下一个关键帧。
T=0 时在起点，T=1 时在终点，中间点按照线性变化规律推进。
适合简单平移或匀速运动的动画控制。

3. 2阶 B 样条（抛物线）

2阶 B 样条引入了中间控制点，生成抛物线形状。

有起点、终点和一个中间控制点，控制物体在路径中呈现出一个弯曲过渡。
这是动画中最早出现曲线轨迹的形式，允许一定的加速度或减速变化。
曲线不会穿过中间控制点，但会受到其影响，路径变得更自然、柔和。

4. 3阶 B 样条（立方曲线）

3阶 B 样条允许两个控制点，可以更自由地控制曲线形状。

可以实现"来回弯曲"的路径，有两次方向变化。
允许制作复杂的运动曲线，例如摆动、缓入缓出、弹跳等。
是最常用于动画中的阶数，因其灵活性和控制力强，动画软件多数默认使用 Cubic B-Spline。

样条曲线的结构组成：

B 样条由关键帧 （Keyframes）和切线手柄（Tangent Handles）组成。

关键帧定义了动画在某个时间点的状态。
切线手柄控制从该关键帧出发或到达的曲线方向与速度。
美术人员可以通过拖动这些控制手柄来"雕刻"曲线，使动画效果更符合预期。

样条曲线的统一性与兼容性：

所有 B 样条实际上都可以通过三阶样条来实现，通过重复控制点（称为"节矩重复"）可以退化为低阶曲线（如线性或阶跃）。
因此一个完全使用三阶样条的动画系统就可以覆盖所有情况，具备极高的通用性和灵活性。

样条曲线不是唯一选择：

虽然 B 样条非常通用，但它并不是创建 F(T) 动画函数的唯一方式。
我们可以根据运动需求直接设定特定的数学函数，如前面讲的抛物线运动，可以通过设定初速度、加速度和时间求解出轨迹方程，而无需使用 B 样条构造。
动画的核心思想是构造一个函数 F(T)，输入时间 T 输出所需状态，不论这个函数是 B 样条、解析方程、噪声函数、或者其它任意方式。

总结：

动画的本质是构建"时间到状态"的映射函数 F(T)。
B 样条是一种广泛使用且直观易控的函数构造方式，适合美术和动画设计师直观地调节动画曲线。
但我们也完全可以脱离样条，使用任何数学函数只要它能根据 T 输出我们想要的动画状态即可。
B 样条之所以常见，是因为它通用、灵活且对非程序人员也友好。

这就是动画中 B 样条的完整结构与思维方式，既是强大工具也是一个思维框架。

黑板：参数空间、状态向量和广义坐标

现在我们已经明确了 F(T) 的概念，知道它是一个函数，输入时间 T T T，输出某种状态，但我们还没有具体讨论这些"状态"到底是什么。F(T) 本身只是一个抽象函数，它生成的是"状态"（state），但在没有明确状态的内容之前，它并没有实际含义。因此，我们需要具体定义我们要生成的状态类型。

游戏中我们关注的"状态"是什么？

在游戏中，我们通常关心的是角色、物体或环境随时间变化的表现状态。这些状态可能是位置、角度、尺寸、形变等，所有这些都可以被看作是某种参数空间（parameter space）中的变量。所谓的"骨骼动画系统"或"关键帧动画"只是这些状态建模方式的一种，不应被视为唯一的标准结构。

我们需要思考的是："我们要生成什么样的参数集合，它们能完整描述出动画中的某个实体？"这才是状态建模的核心。

动画状态的参数化：我们自由决定状态向量的形式

我们可以自由选择任何能够反映动画结果的参数组合。例如：

在之前的例子中，一个角色被建模成一个"地面点"和一个"头部高度"。
地面点是一个三维向量（X, Y, Z），它通过物理模拟获得（如使用 Forward Euler 积分法）。
头部高度是一个标量，由正弦函数控制（如 sin ⁡ ( T b o b ) \sin(T_{bob}) sin(Tbob)）。

这两部分组合在一起形成了一个状态向量（state vector），即：

复制代码

状态向量 = [地面 X, 地面 Y, 地面 Z, 头部高度]

这个四维向量就足够我们在每一帧中计算出角色的渲染位置了。

这不是骨骼动画系统 ------ 但功能上更高效

虽然这个状态也能用骨骼动画系统模拟出来，但那样就得人为建一个骨骼系统并分配一个"骨骼"来代表头部的位置，再去动画这个骨骼的 Y 值，反而复杂化。

而我们使用这个四维状态向量则不需要任何骨骼结构：

效率更高：因为我们知道头部只能在垂直方向上移动，我们只需要一个标量就可以控制它，而不是完整的三维空间位移。
状态更清晰：我们直接表达我们关心的变量，不必引入额外的结构去"绕弯子"实现。

状态向量是动画的核心

动画系统的本质就是：定义一个状态向量，然后编写 F(T) 来生成这些状态。

每一个时刻的动画状态，都是这个状态向量的一个实例。只要我们有一个良定义的 F(T) 函数，我们就可以持续生成这些状态，并传递给渲染系统做可视化。

重要的是：状态向量必须至少包含所有必要的信息，能让我们最终绘制出动画对象的样子。它可以是最简形式，也可以冗余一些，但不能缺失关键的"决定可视化"的信息。

动画系统如何使用状态向量？

初始化状态向量：确定对象在起始时间的状态。
使用 F(T) 生成状态：F(T) 可以是解析函数、数值积分、样条曲线或任何其他函数形式。
每帧更新 ：输入新的时间点 T T T，F(T) 输出新的状态向量。
渲染：根据当前状态向量，将对象正确绘制在场景中。

总结核心思维方式：

动画的本质是 F(T) → 状态向量。
状态向量自由设计，包含所有必须信息，用于渲染。
骨骼系统、关键帧系统等只是具体实现方式，本质都是对状态空间的不同封装。
状态不一定要通过传统方式实现，我们可以用更高效、定制化的方式组合状态变量。
所有动画系统最终都依赖于良定义的参数空间和随时间演化的 F(T) 函数。

掌握这些本质后，我们就能构建出灵活、精确且高效的动画系统，不再受限于传统框架的束缚。

黑板："位置向量"与"状态向量"

我们现在进一步明确动画系统中需要关心的两个关键要素：状态向量（State Vector） 和 位置向量（Position Vector）。它们在动画的更新与渲染过程中扮演着不同的角色，并具有清晰的职责划分。

状态向量与位置向量的区别与关系

状态向量（State Vector）

状态向量保存的是我们在每一帧中必须保留、并通过时间推进更新的数据，是动画系统"记忆"的内容。它包含能够完整推导出可视化数据所需的最小变量集合，具有时间上的连续性，适合被微分、积分等数值方法操作。

例如，在一个简单的例子中：

地面点位置 (gx, gy, gz)：通常通过物理仿真计算出来（如使用 Forward Euler）。
头部起伏参数 t_bob：通过动画函数（如 sin 函数）生成。

于是我们得到了一个状态向量：

复制代码

状态向量 = [gx, gy, gz, t_bob]

其中：

gx, gy, gz 随时间推进而更新，代表物体在世界空间中的运动。
t_bob 是一个控制头部起伏的时间参数，同样随时间线性增长。

位置向量（Position Vector）

位置向量是在当前状态向量的基础上，推导出来的用于最终渲染的世界空间坐标。它可以是状态向量的部分拷贝，也可以是状态向量的非线性函数。例如：

对于地面点位置，直接从状态向量中拷贝即可。
对于头部高度，可能是 sin(t_bob)，需要从状态向量中计算。

于是位置向量为：

复制代码

位置向量 = [gx, gy, gz, head_height]
head_height = sin(t_bob)

我们将状态向量推进一帧之后，根据其数值计算出位置向量，再传给渲染系统进行实际绘制。

动画的更新流程

保存状态向量

我们在内存中保存状态向量，它是动画系统运行的核心数据。
更新状态向量

每帧调用动画更新逻辑（如微分方程或正弦函数增长）对状态向量进行推进。
生成位置向量

从状态向量中，计算出实际要渲染的坐标，比如计算 head_height = sin(t_bob)。
渲染

将位置向量作为输入，交给渲染系统进行绘制。

补充概念：广义坐标（Generalized Coordinates）

从机器人学和动力学的角度来看，状态向量中的元素，也可以称作广义坐标（generalized coordinates）：

它们是描述系统自由度最小、最自然的一组参数。
在动画系统中，如果我们把"状态向量"看作是储存用来计算的状态，那么这些"广义坐标"其实就是它的本体，它们的变动决定了角色的姿态与行为。
不同于渲染向量，广义坐标不一定是可见的位置，而是产生可见状态的最本质参数（如角度、时间参数、速度等）。

命名上的小讨论

在实际实现中，这些数据结构的命名可能会有所不同，例如：

有人可能把 gx, gy, gz, t_bob 叫做 "State Vector"
把计算出来的 [gx, gy, gz, sin(t_bob)] 叫做 "Position Vector" 或 "Pose"
有人会使用机器人学中的 "Generalized Coordinates" 来称呼状态变量

虽然命名不同，但结构本质和逻辑是一致的。

总结

动画系统的核心就是：用状态向量模拟时间推进 → 用该状态生成渲染数据
状态向量保存的是动画所需的最小自由度集合，是动画函数 F(T) 的输入和演化核心。
位置向量是从状态向量派生出的可视化结果，用于渲染。
整个动画系统的更新循环就是围绕状态向量和位置向量不断运作的。
这一思路比传统"骨骼动画"更灵活、通用，可以适用于各种非传统动画结构。

掌握这个流程后，我们能更自由地设计与实现任何形式的动画系统，而不必受限于某种具体范式。

黑板：动画管线：存储 -> 渲染输入 -> 精灵列表

我们可以将动画系统的工作过程画成一个清晰的分层流程图，它包括三个主要阶段：存储数据 → 渲染输入 → 实际渲染结果。下面详细解释各个环节是如何运作的。

第一阶段：存储的数据（Stored Data）

这一部分是动画系统每一帧所保存的核心参数，也是整个动画逻辑的驱动源。这些数据构成了状态向量，用于描述动画中对象的最基本自由度和运动控制变量。

例如，在一个简单角色系统中，存储的数据包括：

地面位置 G = [gx, gy, gz]：角色所站立的地面点坐标。
动画参数 t_bob：控制角色头部上下浮动的时间变量（例如正弦曲线的参数）。

这些值是随着时间持续更新的，是我们用来计算动画状态的输入。

第二阶段：渲染输入（Render Input）

这一阶段是从状态向量中推导出的中间变量，用于生成物体的具体空间位置，是我们最终传递给渲染系统的关键参数。

例如：

地面位置 G = [gx, gy, gz]：可以直接从状态中拷贝。
头部高度 H = head_height = sin(t_bob)：由 t_bob 计算得出，表示头部在垂直方向的浮动量。

此时我们可以构造出一个渲染输入向量：

复制代码

RenderInput = [gx, gy, gz, head_height]

它提供了生成物体几何变换所需的全部空间信息。

第三阶段：渲染生成（Render Output）

在这一步，我们根据渲染输入的数据生成场景中的**具体可见对象（精灵、网格、实体等）**的世界空间位置。

例如，我们渲染的只是一个头部实体，这个头部在空间中的最终位置为：

复制代码

头部位置 = 地面位置 + 头部高度 * 向上单位向量
         = [gx, gy, gz] + head_height * [0, 0, 1]

这一步我们通过向 G 向量加上 head_height 沿 Z 轴的偏移，从而得到了头部在世界空间中准确的位置。

最终我们构造出一个**精灵列表（sprite list）**或其他稀疏渲染数据结构，包含：

头部的空间位置
可能还有姿态（如朝向）、缩放、材质等

总结：完整流程结构

复制代码

[Stored Data]
   ↓
   （状态更新，如微分、函数评估）
   ↓
[Render Input]
   ↓
   （位置计算，例如向上偏移等）
   ↓
[Render Output / Sprite List]

关键特性总结如下：

存储数据 是动画系统主动维护和推进的核心变量，控制所有动作。
渲染输入 是通过对状态向量求值得到的、用于构建空间姿态的中间数据。
渲染输出 是真正提交给图形引擎的最终数据，表示物体实际要出现的位置或姿态。

这个结构是一种高度通用的动画构造方式。通过拆分为多个阶段，我们可以：

灵活定义各种动画参数
精确控制渲染行为
更轻松地将动画与物理模拟、输入控制、AI逻辑等模块集成

它也是现代游戏与图形系统中通用的一种动画组织结构。

黑板："骨骼动画"

我们如果决定使用一个骨骼动画系统（skeletal animation system） ，本质上就是对动画系统中的状态建模进行结构化、标准化 。我们不是再允许状态向量任意扩展、任意定义，也不允许渲染数据由各种自由函数组合生成，而是采用一种统一的、固定的表达方式来描述动画状态。

骨骼系统的核心思想

我们将动画系统的"状态"标准化为一组骨骼（bones），每一个骨骼都拥有一组固定的属性，而不是为每个动画需求量身定制不同的参数结构。这样做的基本逻辑是：

所有动画对象都以相同结构表示
动画变换流程可以统一处理，易于通用化计算
渲染阶段也可以通过通用骨骼结构计算出最终位置

每个骨骼包含的标准属性

我们统一规定，一个骨骼（bone）至少包含以下几个字段：

平移向量（Translation）：
- tx、ty、tz ------ 空间位置偏移
旋转值（Rotation）：
- 在2D中，只需要一个角度值 θ 表示绕 Z 轴的旋转（2D 只需要绕一个轴旋转）
缩放因子（Scale）（可选）：
- 通常为一个或三个值，表示骨骼的大小缩放

换句话说，我们每一个骨骼状态就是一个包含固定维度的向量，例如：

复制代码

[tx, ty, tz, θ, sx, sy, sz]

而整个动画对象，就是这些骨骼向量的数组（list of bone vectors）。

系统的规范化 vs 灵活性的折衷

这种做法的好处是：

简化了动画流水线处理逻辑
统一了渲染系统的输入结构
可被多种工具链（如导出器、编辑器、运行时）通用支持

但是这种结构也带来了一定的局限性，尤其在 2D 动画开发中 显得格外突出：

很多时候我们希望通过某种奇异函数或特定逻辑控制动画中的某个部分（如复杂弹跳、抖动、随时间变化的高度等）
若使用骨骼系统，那我们必须以骨骼结构封装这些自定义逻辑
例如，若只需要一个数值控制一个点的上下浮动，在骨骼系统中却不得不为它创建一个完整骨骼（带 XYZ 位置、旋转、缩放），这就显得冗余

因此，在一些场景中，我们会觉得骨骼系统是"过于僵化"的，不利于表达灵活控制逻辑。

总结：骨骼系统在动画架构中的定位

我们可以把骨骼动画系统看作是在动画控制流程中插入的一个"模板化约束"层：

它用来简化和通用化渲染前的状态表达
但它限制了状态向量的结构自由度
如果不想使用骨骼系统的刚性结构，可以选择手动定义任意参数和函数来驱动状态演变和渲染逻辑

骨骼系统并不是动画系统的本质，而是一种用于工程简化和结构统一的策略。理解了这一点之后，就可以根据需求自由选择是否使用骨骼系统。

黑板：渲染动画

我们目前已经在做一些基础的动画系统，实现效果基本可行，因此我们也逐渐熟悉了它的运行方式。接下来，我们需要深入探讨渲染阶段的实现细节，因为这部分仍有不少值得改进的空间。

举例说明：角色跳跃的动画系统

以游戏中的主角为例，假设他在执行一个抛物线跳跃动作。在这个场景中，我们可以将角色的动作简化为以下几个元素：

抛物线轨迹 ：这是角色的移动路径，是通过一个随时间变化的函数 f(t) 来计算的
角色身体：可以表示为一个主干（躯干）
附属物体：例如披风，在角色移动时会随之摆动或飘动

我们已经实现了基础版本的 f(t)，让角色沿着抛物线轨迹跳跃，这种实现是最基础的状态转换控制。

基础动画 vs 专业级动画的差异

虽然这种方法能完成角色运动的核心功能，但从表现效果来看，这还远远不够。很多独立游戏确实也只做到这个程度，但我们希望能做到更高质量、专业级别的动画效果。

为了达成这一目标，需要引入更多传统动画的原则，尤其是：

预备动作（Anticipation）：
- 在主动作之前进行的"准备姿势"，例如角色在跳起之前先下蹲
- 预期动作能传达意图、增加真实感
延续动作与收尾（Follow-through）：
- 动作结束后仍有一部分身体（如头发、披风）继续运动，体现惯性
- 让动作显得更有质感、更自然

目前我们系统生成的轨迹函数只是简单地控制了"位移"，而没有体现任何预备或延续，导致动作虽然"可用"，却缺乏"表现力"。

改进方向

为了使动画系统更有表现力，我们将逐步完善以下几个方面：

添加额外参数控制：不仅控制位置，还控制速度、加速度、旋转角度、变形程度等
细化阶段划分：例如将跳跃分为下蹲准备、起跳、空中、落地等阶段
引入次级动画：例如披风、手臂、装备等附属结构也通过独立函数或物理仿真控制
提升函数设计质量：例如利用曲线插值、周期函数、缓动函数等手法制作更自然的运动轨迹

后续计划

由于渲染部分还没深入讨论，因此在接下来的内容中，将进一步介绍动画渲染的流程，同时也可能补充一些代码示例，用来展示这些状态是如何从函数生成，并最终驱动渲染的。

我们将以已有的 f(t) 函数为基础，拓展出动画表达力更强的版本，从而真正使角色在游戏中"活起来"。

网络：生命的幻觉：迪士尼动画1 《生命的幻象：迪斯尼动画造型设计》好像是叫这个

在动画系统开发过程中，虽然我们在编程上可以控制状态、函数、轨迹等内容，但如果想要真正理解动画的本质、提升动画质量，仅仅靠技术手段是不够的。

动画从业者必须掌握的基础知识

我们在这里要明确一点：任何参与动画系统开发的程序员都应该系统学习动画艺术的基本原理。如果没有深入学习相关理论，对动画效果的判断就会流于表面，不理解"目标"是什么，无法识别什么是好的动画、什么是糟糕的表现，做出来的东西可能技术上是"能跑的"，但艺术上完全不成立。

因此，有一本非常重要的经典书籍，每个动画相关的程序员都应该从头到尾仔细阅读，这是绝对必要的。这本书不仅涵盖了动画的基础原理和核心原则，还帮助我们建立判断标准，使我们在编码时具备清晰的目标感。

理解动画：不仅仅是代码问题

我们不会在此详细介绍动画背后的艺术动机，例如什么历史背景下诞生了某个动画原则，或是什么美学逻辑让动画看起来更自然------因为这是一个庞大且偏重美术的领域，需要系统地艺术训练与理解。

但即便如此，作为程序员，我们至少需要做到以下几点：

了解动画术语和概念

比如"缓入缓出"、"提前准备"、"拖拽"、"延续"、"关键帧"、"次级动作"、"重心"、"剪影"等等。这些概念对我们实现动画系统有直接影响。
知道动画的结构组成

包括帧率选择、时长安排、过渡处理、动作曲线建模等技术手段如何配合艺术需求。
理解动画的意图表达

明白动画并非纯粹的移动或变化，而是角色性格、情绪、意图的体现。

编程实现只是传达的手段

我们在之后的开发中，会继续展示各种动画原则的实现方式。但实现只是"怎么做"，真正的"为什么这么做"，必须建立在艺术理解的基础上。

我们将用编程的方式表达这些概念，用状态更新函数、插值函数、刚体模拟等方式去"编码"这些动画原则。我们不会去追溯某个动画原则的历史背景、也不会讨论它是如何从某位艺术家实践中诞生的，因为这不属于我们当前的任务范围。但我们会保留这些原则的名称，并尽可能忠实地用程序再现其效果。

小结

作为动画系统的开发人员，我们的目标不仅是"让物体动起来"，而是"让运动有生命、有表现力、有逻辑"。如果缺乏艺术理论支撑，那么再复杂的系统也只是僵硬的数据转换。因此，哪怕我们只做底层实现，也必须拥有基本的动画理解力，才能做出真正有意义的动画系统。

黑板：预期和跟随

在当前的跳跃动画实现中，角色的运动是直接按照一条抛物线进行的，没有任何缓入（ease-in）或缓出（ease-out）的处理，也缺乏"anticipation"（预备动作）和"follow-through"（延续动作）这两个经典动画原则的体现。

当前实现存在的问题

我们现在的动画系统是这样的：

一旦进入跳跃动作，就直接开始沿抛物线运动；
动作开始和结束时没有任何过渡；
起跳和落地都是"瞬间完成"的，缺乏现实中的惯性和动势；
实际看起来非常"机械"，没有"重量感"与"动感"。

虽然在物理意义上，物体一旦进入抛物运动，其速度变化确实只受到重力影响，不再存在加速度或减速度，这是正确的。但真正缺乏的是动作开始之前角色是如何获得上抛速度的那部分内容。

Anticipation（预备动作）

在现实中，如果我们想要跳起来，必须先下蹲蓄力，压缩身体，就像弹簧一样，然后才爆发出跳跃的动力。这一系列动作就是"anticipation"。

目前的系统完全跳过了这一步，角色就好像突然获得一个向上的初速度一样，显得非常突兀且不真实。

动画增强的需求

为了让动画更真实、有表现力，我们希望：

在正式跳起之前，有一段"预备阶段"，表现出角色蹲下的动作；
这段预备动作不应该影响跳跃轨迹的F(t)函数本身；
而是要在时间轴上"插入"一段额外的时间用来表现这个过程。

技术思路：时间窗口分区（T分段）

我们当前的跳跃轨迹F(t)是一个定义在 [0, 1] 区间上的函数：

T=0：跳跃开始；
T=1：跳跃结束。

如果我们要在跳跃开始之前插入一段 anticipation（例如 0 <= T < 0.1），那么：

原本跳跃运动应该从 T = 0.1 开始而不是 T = 0；
在 0 <= T < 0.1 这段时间里，角色应该保持在地面，并执行下蹲或身体压缩的预备动作；
这个段落并不改变抛物线函数本身，只是延长动画表现的时间。

实现策略

我们可以通过以下方式来实现时间分段：

定义总时间区间为 [0, 1]；
划分两个阶段：
- T ∈ [0.0, 0.1]：anticipation 阶段；
- T ∈ [0.1, 1.0]：主跳跃动作阶段；
在动画驱动函数中判断当前T所在的区段：
- 如果在anticipation阶段，角色保持地面位置，并播放"下蹲"动作；
- 如果在跳跃阶段，输入 t' = (T - 0.1) / 0.9 到 F(t') 中进行抛物运动；
  
  注意，这样做相当于将跳跃动作压缩进了 0.9 的时间区间中。

小结

我们通过对T时间轴进行分区，将跳跃动画的"准备"和"跳跃"两个阶段区分开来：

保持了F(t)函数作为跳跃轨迹函数的纯净性；
增强了动画表现力，让动作看起来更自然；
为后续加入follow-through（比如落地时身体震动）等阶段奠定了基础。

这种做法不仅适用于跳跃，也适用于几乎所有具有"阶段性"的动作动画，是构建高质量动画系统的基本方法。

黑板：使用"映射到范围"将动画阶段拆分

我们要实现一个更加自然、具有"anticipation（预备动作）---ballistic（主运动）---follow-through（后续动作）"结构的跳跃动画。为此，我们需要将原本简单的时间变量 T ∈ [0, 1] 映射成多个分段区间，分别用于不同的动画阶段。

为了完成这种动画的时间控制，我们需要进行"归一化区间映射（map into range normalized）"。该过程包括以下几个关键点：

动画阶段划分

我们将完整的 T ∈ [0, 1] 时间段划分为三部分：

预备阶段（Anticipation）：角色准备跳跃的阶段，可能是下蹲蓄力。
主运动阶段（Ballistic）：角色处于抛物线运动中的阶段。
后续阶段（Follow-through）：角色落地并收尾动作的阶段。

这些阶段被称为 launch（起跳）和 land（落地），例如：

T_jump = 0.3 起跳点
T_land = 0.8 落地点

对应分段T值生成

我们希望在每个阶段内部再创建一个局部的 T 值，也就是：

[0.0, T_jump] → 阶段0的 T 值 ∈ [0, 0.3]
[T_jump, T_land] → 阶段1的 T 值 ∈ [0.3, 0.8]
[T_land, 1.0] → 阶段2的 T 值 ∈ [0.8, 1]

所以，我们的目标是：

通过一个全局 T 值（例如 T = 0.35）判断当前处于哪个阶段；
然后将该 T 映射到该阶段的本地 T ∈ [0, 1] 范围内；
同时记录当前阶段编号（phase index：0, 1, 2）。

实现方式

我们已实现了一个数学函数，可以进行这个归一化映射：

c 复制代码

float MapIntoRangeClamped(float t, float t_min, float t_max)
{
    return Clamp01((t - t_min) / (t_max - t_min));
}

该函数作用是把全局 T 值归一化到指定区间 [t_min, t_max] 中，再压缩到 [0, 1] 的范围。

在使用时，只需写出：

c 复制代码

float local_t = MapIntoRangeClamped(T, T_jump, T_land);

就可以把 T 映射到 T_jump 到 T_land 的范围内，并返回 [0, 1] 的值供该阶段使用。

应用场景

这个归一化分段是实现复杂动画（如自然跳跃动作）的基础。通过这种方法，我们可以在每个阶段内部定义不同的动画曲线，例如：

阶段0 使用 ease-in 曲线模拟下蹲；
阶段1 使用标准抛物线；
阶段2 使用 ease-out 曲线模拟落地缓冲。

后续优化

虽然目前代码中是手动书写这些分段和映射逻辑，但后续可以考虑构建一个通用动画阶段系统，使阶段划分和局部 T 值生成更加模块化和可复用。

这种对动画时间的精细化管理，是让动画从"能动"变成"动得漂亮"的关键所在。通过为每个阶段单独设计表现和节奏，动画将更具生命力和艺术表现力。

game_world_mode.cpp：将这些阶段添加到身体的跳跃动画中

我们在跳跃动画中，为了实现自然的运动过渡和阶段控制，需要对时间变量 T 进行精细化的分段处理。我们将跳跃过程拆分为三个阶段：起跳阶段（Jump） 、抛物阶段（Ballistic） 和 落地阶段（Landing） 。这三段分别对应角色跳跃准备、空中飞行和着陆缓冲的动作。为了驱动这三段动画，我们需要判断当前 T 值处于哪个阶段，并对其进行归一化映射和逻辑处理。

动作阶段判定逻辑

在更新跳跃状态时，我们根据当前全局 T 值进行判断：

如果 T < T_jump，说明当前处于起跳阶段。
如果 T < T_land，说明处于抛物阶段。
否则，进入落地阶段。

这样就能在动画逻辑中明确分支处理每个阶段：

c 复制代码

if (T < T_jump) {
    // 起跳阶段
} else if (T < T_land) {
    // 抛物阶段
} else {
    // 落地阶段
}

抛物阶段中的 T 映射与动作实现

当处于抛物阶段 时，需要将当前全局 T 映射到 [T_jump, T_land] 范围内，并压缩为 [0,1] 的局部 T 值，方便用于动画函数：

c 复制代码

float t_mapped = MapIntoRangeClamped(T, T_jump, T_land);

这个局部的 t_mapped 会被用于抛物线轨迹函数，例如：

c 复制代码

position.y = Parabola(t_mapped);

此外，水平速度（DP）在这类动画中不需要处理，因此设置为 0。

起跳与落地阶段的处理与补充

虽然抛物运动在物理上是连续的，但我们在落地点 T_land 可能不会精确命中（因为帧率离散导致跳过），所以需要在检测到 T 进入落地阶段时，强制将角色定位在最终位置，防止出现悬浮或穿地：

c 复制代码

if (T >= T_land) {
    position = final_landing_position;
}

这一修正可以避免角色跳跃后在最后位置偏移或不准确落地的问题。

调试反馈与现象观察

实际运行时观察动画效果，角色的跳跃虽然看起来"飞"了出去，但实际上没有完整地落地，问题出在：

T 没有恰好等于 T_land 时进入判断；
因为跳跃速度较快，跳过了 T_land，直接进入了落地阶段；
所以没有执行完整的抛物线终点。

为了解决这个问题，我们在进入落地阶段时，手动补上最终位置设定，确保视觉上跳跃动作闭环。

小结：完整动画时间分段处理流程

设定时间点：T_jump 和 T_land
用 T 判断当前阶段（起跳 / 抛物 / 落地）
使用 MapIntoRangeClamped() 映射局部 T ∈ [0, 1]
在抛物阶段使用轨迹函数生成位置
落地阶段补充终点位置，避免跳跃脱节

通过这些处理，跳跃动画变得分阶段、可控、自然，并具备一定的艺术表现力。接下来可以继续拓展 easing 曲线或动作衔接逻辑，让整体动作更加丰富流畅。

运行游戏并查看跳跃

我们现在已经完成了对跳跃动画的时间窗口分割（windowing），将整个跳跃过程拆分为起跳、抛物、落地三个阶段，并正确实现了 T 值的映射，使得每个阶段都拥有独立的局部时间范围。然而，当前仅仅完成了时间划分，并没有在这些阶段中实际加入不同的动画处理逻辑。接下来我们可以进一步扩展，思考如何在每个阶段中实现更具表现力和真实感的动画效果。

阶段内可以实现的细节动画（可扩展方向）

起跳阶段（Anticipation）
- 模拟人物下蹲蓄力的动作。
- 缩放身体比例（例如 Y 缩短，X 稍微放大）来表现"压缩"感。
- 加入抖动或缓冲效果，例如使用非线性插值（ease-in）模拟准备起跳的过程。
抛物阶段（Ballistic）
- 使用完整的抛物轨迹函数控制位置变化。
- 可以对角色进行倾斜旋转，例如空中翻转等视觉效果。
- 根据飞行进度调整身体姿势，比如空中拉伸、手脚摆动。
落地阶段（Follow-through）
- 落地时增加惯性动作，比如身体下沉、腿部缓冲。
- 使用 ease-out 曲线使动作渐缓结束。
- 加入落地尘土或震动反馈等细节效果。

动画控制方式建议

为了实现上面这些效果，可以通过以下几种方式控制动画：

使用 插值函数（Interpolation） 控制每个阶段的具体动作强度与速度，如线性插值、三次贝塞尔曲线、ease-in/ease-out 等；
结合 骨骼动画 或 帧动画 切换不同姿态；
对局部属性如位置、缩放、角度进行动态修改。

动作阶段逻辑结构可以这样组织：

c 复制代码

if (T < T_jump) {
    float t_local = MapIntoRangeClamped(T, 0.0, T_jump);
    DoAnticipationAnimation(t_local);
}
else if (T < T_land) {
    float t_local = MapIntoRangeClamped(T, T_jump, T_land);
    DoBallisticAnimation(t_local);
}
else {
    float t_local = MapIntoRangeClamped(T, T_land, 1.0);
    DoLandingAnimation(t_local);
}

这样我们可以根据局部 t 值，在每个阶段中自由添加动画逻辑，而不仅仅是位置移动。

小结

目前的系统虽然已经实现了跳跃动作的结构性时间分段处理，但暂未在各个阶段中添加具体的动画表现。接下来，我们完全可以利用这套时间窗口机制，在不同阶段中引入更加细致、物理真实和视觉吸引力的动画内容。这样不仅提升角色动作的流畅度和表现力，也为后续支持更多动作样式（如翻滚、滑铲、二段跳等）提供良好的扩展基础。

game_world_mode.cpp：给身体一些弹性

我们目前并没有任何机制来表示披风距离身体的高度，也就是说，系统中没有明确体现披风在跳跃过程中的垂直偏移。因此，我们需要一种方式来动态控制这个高度。为了解决这个问题，我们计划使用 t_bob 参数来驱动披风的上下起伏动作，尤其是在起跳阶段的动画中使用该值来体现自然的披风反应。

披风上下运动的目标

我们希望披风在角色起跳的初期阶段能表现出自然的晃动感，即在角色下蹲起跳的过程中，披风向下拉伸，然后在角色跃起的同时向上飘起。因此，披风的运动需要先向下，然后回到正常位置，呈现出一种周期性振动的感觉。这种效果可以用正弦波来近似模拟。

正弦函数的基本想法

正弦函数在区间 [0, π] 内呈现出"先下再上"的变化趋势，完美契合我们对披风动作的期望：

sin(0) = 0：初始位置；
sin(π/2) = 1：最下沉；
sin(π) = 0：回到正常高度。

因此，我们可以用 t_bob 作为正弦函数的输入，控制披风的偏移程度。

动态生成 t_bob 值的方式

我们需要将跳跃的时间区间 [T=0, T_jump] 映射为 [0, π]，从而将线性时间进度转换为正弦值：

c 复制代码

float t_local = MapIntoRangeClamped(T, 0.0, T_jump); // 映射到 [0, 1]
float t_bob = sin(t_local * PI); // 映射到 [0, π] 后求正弦

然后将 t_bob 应用到披风的垂直位移中，例如：

c 复制代码

cape_offset_y = base_offset + t_bob * bob_amplitude;

其中 bob_amplitude 是我们设定的最大偏移量。

小结

通过引入 t_bob 并结合正弦函数，我们为披风提供了一个动态变化的高度参数，使其在起跳动画的阶段表现出更真实的惯性晃动效果。这种处理不仅能提升视觉表现力，还能增强动画的物理合理性和动作层次感。这个参数还可以在其他动作中复用，比如落地或跑步，增强整体角色的动态感。

黑板：使用正弦曲线计算动画曲线

我们在实现披风动画时，为了模拟自然的上下摆动效果，决定利用正弦函数的特点来生成一个"从0上升再回到0"的值，用来驱动披风在跳跃过程中的垂直偏移。

正弦函数的应用逻辑

我们需要让披风的垂直偏移在跳跃初期呈现一个"上下回弹"的动态，即先下沉再回升到正常位置。我们利用正弦函数在区间 [0, π] 上的行为实现这一点：

sin(0) = 0，跳跃开始时披风在正常位置；
sin(π/2) = 1，跳跃中段披风达到最大下沉；
sin(π) = 0，跳跃结束时披风回到正常位置。

为了将动画的时间参数 T（范围为 0 到 1）映射到正弦输入区间 [0, π]，我们用公式：

c 复制代码

t_bob = sin(T * PI);

这个公式将时间线性转换为一个带有回弹感的浮动值，完美用于模拟披风在跳跃中下垂并回弹的自然状态。

将 t_bob 应用于披风垂直偏移

计算出 t_bob 后，我们用它来调整披风的垂直位置。例如：

c 复制代码

cape_offset_y = base_offset + t_bob * amplitude;

其中：

base_offset 是披风的默认垂直位置；
amplitude 是偏移的最大幅度（决定披风晃动的剧烈程度）。

图形渲染中的集成

为了在视觉上看到实际效果，我们将该偏移应用到披风的绘制逻辑中。在绘制披风的位置时加入垂直偏移量：

c 复制代码

draw_cape(y_position - cape_offset_y);

我们尝试了负方向的偏移，也许想让披风"上飘"而非"下垂"，可以根据实际视觉调整方向。

为了更好观察效果：放慢动画速度

当前动画速度太快，肉眼难以观察披风的变化细节。因此我们将整体动画时间放慢为原来的六分之一，以便清晰看到披风在跳跃初期的动态：

c 复制代码

delta_time *= 0.166f; // 原速的 1/6

这让我们能更容易调试、微调 t_bob 的生成逻辑与动画表现。

小结

我们通过 sin(T * PI) 公式，实现了跳跃初期披风自然的上下晃动效果，形成了一个带有物理弹性的视觉反馈。结合动画速度控制，这一系统将更具表现力与真实感，是细节动画中非常有效的一个技巧。

运行游戏并查看弹性效果

我们目前已经基本实现了披风在跳跃过程中的回弹动画，从效果上来看，哪怕只做了非常简单的处理，也已经能够带来明显的视觉改进，让动作更具"跳跃感"。

披风绘制的层级问题

我们希望披风绘制在角色身体之上，因此需要确保绘制顺序正确。目前资源的排序似乎存在问题，美术资源被堆叠在一起，导致披风可能被挡住。为了临时解决这个问题，我们先手动设置一个偏移值让披风绘制时向上挪动一小段，以便在视觉上处于身体之上。不过这只是权宜之计，未来仍需使用更合理的图层系统或深度排序逻辑。

效果初显：披风动态提升了整体动画质感

即使只加入了一个简单的基于正弦曲线的垂直摆动（t_bob），也可以很明显地感受到人物在跳跃时的动势更自然、更有弹性：

披风在起跳瞬间有"被动下垂"的反馈；
中途自然回弹；
末尾回到初始位置，完成完整动态循环。

这提升了动画的表现力，使得跳跃更具生命力，而不是"死板地沿抛物线移动"。

资源位置的临时修正与隐患

目前为了让披风在画面上正确显示，我们使用了硬编码的偏移量将其上移，这种做法虽然短期内有效，但会带来以下问题：

披风和角色其他部分之间的位置关系容易失调；
不同分辨率或缩放下表现不一致；
在后续加新动作或角色变化时容易出错。

因此我们后面需要引入更规范的图层控制方式，比如设置绘制排序权重或使用Z轴坐标模拟深度感。

后续计划

虽然初步效果达到了预期，但当前实现方式仍不完善，我们需要进一步优化：

完善披风与身体之间的相对绑定逻辑；
改进图层排序方式，彻底解决"谁在上面"的问题；
在更多动作中复用 t_bob 或类似控制参数，形成一致的物理反馈系统。

小结

即使是极其简单的一段正弦动态，加上一点绘制顺序上的调整，也能显著改善角色动作的表现力。披风的自然摆动，使得整个跳跃动作更加可信，整体动势更加饱满。接下来需要从结构上解决资源层级问题，并逐步完善披风系统的通用性。

game_world_mode.cpp：为弹道阶段做动画

在此阶段，目标是让跳跃过程中披风的动态更加自然，并且能够更好地衔接各个阶段的运动。例如，在跳跃的 T_jump 阶段，披风的动作应当与角色的动作相协调，并且能够体现出连续性。具体来说，期望让披风的摆动更加流畅，避免突然的静止或停滞感。

目标：让动态更加连贯

为了实现这一点，需要让披风在跳跃的不同阶段都能有适当的运动。例如在 T_jump 阶段，披风应该随着角色的起跳进行一系列自然的摆动，类似于物理上的"惯性"效果，即使在进入弹道阶段时，披风也不应突然停止，而是应当继续自然摆动。为此，需要将运动的整个时间范围（如 T_jump 到 T_land）映射到一个更大的运动周期中，让披风的动态能够覆盖整个 tau 范围。

时间窗口的重叠

在实现这一点时，考虑到不同的运动阶段（跳跃、弹道、着陆），需要确保这些阶段之间能够重叠进行。具体来说，可以通过将 T 值映射到一个更大的时间范围，允许跳跃阶段和弹道阶段的运动相互交替，保证披风的动态表现出更强的连贯性。

例如，可以使用如下逻辑：

当 T 小于 T_mid（跳跃阶段和弹道阶段的中间点）时，披风的动态应当呈现出跳跃的自然弯曲；
在 T_mid 到 T_land 的阶段，披风的运动应当平滑过渡，继续按照预定的轨迹完成摆动。

处理重叠时的逻辑问题

在实现过程中，需要注意不能直接重写 T 值，因为如果直接修改 T，会导致运动阶段的划分出错。因此需要确保时间映射是严格的，并且保证每个阶段的运动都有正确的时间控制。如果要让各个阶段的动态能够同时生效，就必须避免直接覆盖 T 值，而是通过适当的时间映射来实现这一目标。

总结

为了让角色的跳跃和披风动态更加自然，需要对跳跃过程中的每个阶段进行精细控制。通过合理的时间映射和运动重叠，可以确保披风的运动从起始到着陆始终保持流畅与连贯。这要求在编程时要特别注意时间值的映射和阶段重叠的处理，避免直接修改时间值，确保每个阶段的动态都能正确地反映出来。

运行游戏并检查跳跃效果

通过加入之前提到的动态调整，现在的跳跃看起来明显更自然了。虽然我们还没有做很多修改，仅仅是增加了披风的动态变化，就让整个动作变得更加生动和逼真。这种改变使得跳跃的过程显得更有层次感，类似于实际跳跃中角色身体和披风的反应。

接下来，着陆阶段也需要进行类似的处理。在着陆时，可以考虑将披风的动态与角色的动作进行结合。例如，随着角色的着陆，披风的摆动应该逐渐减缓，最终稳定下来。这样，披风的运动就能与角色的动态流畅地衔接，确保动作的连贯性和自然感。

总的来说，通过对跳跃和着陆阶段披风动态的精细调整，整个动画的表现会更加真实和具有表现力。

game_world_mode.cpp：给落地动画添加跟随效果

我们采用了与跳跃起始阶段相同的处理方式来优化落地阶段的披风动态。具体做法是从着陆时间点 T_land 开始，一直到动画的结束时间，对披风的运动轨迹进行控制。这个处理逻辑非常直接，没有特别复杂的内容，只是将之前的技术应用在新的时间窗口上。

为了实现这一点，我们依然使用了映射函数，将全局的时间 T 映射到局部的 0 到 1 区间内，并基于这个局部时间值生成披风的运动幅度。在这个阶段，我们让披风的运动呈现一个"冲击---回弹"的小幅度动态，用来模拟角色落地时的惯性反馈。

但不同于起跳时的完整振荡（也就是从 0 上升到 1 再回到 0），在落地阶段我们只需要半个振荡周期，这样披风只会从静止状态上升至一个峰值，随后恢复，而不是继续波动下去。这样可以避免落地动作显得"太跳跃"或失真。

这个微小的变化让落地的反馈更加克制和自然，同时保持了视觉上的节奏感与动画连贯性。最终，角色的整个跳跃动作，无论是起跳、腾空还是落地，都通过披风的细节动画被连贯地整合起来。整体动画因此更具动势、真实感和表现力。

运行游戏并检查跳跃

我们接下来还应该考虑的一件重要事情是跳跃动作的衔接优化，尤其是当角色落地后立即再次起跳的情况。

当前的设计中，披风的上下浮动效果（即 t-bob 的振荡）在起跳阶段和落地阶段分别有各自的运动轨迹：起跳时完整的正弦波动，落地时半个波动。如果角色连续跳跃，也就是说在刚落地时又马上跳起，这样披风在时间轴上会产生重叠的两个振荡区间，从而导致"二次振荡"的现象，使得动画显得不连贯甚至"抖动"。

为了解决这个问题，我们希望能够对这种连续跳跃的情况进行"对齐"处理。也就是说，当落地之后立即跳起时，不应该重新从零开始披风的振荡，而是让新的振荡从前一个运动的自然延续处接上，这样就不会出现重复或突兀的跳跃波形。

实现这个目标的方式是：在检测到角色将要进行连续跳跃时，不重新初始化 t-bob，而是根据当前振荡的位置，计算出合理的起始点，使波形平滑过渡。换句话说，我们要把多个跳跃之间的 t-bob 动态合并成一个连续的波形，从而提升动画整体的流畅性和自然性。

由于时间关系，目前还没有进行这个处理，但这是下一步需要实现的重要内容。通过这种优化，我们可以让动作更加连贯，角色表现更具动势，进一步增强整体的观感。

game_world_mode.cpp：加速跳跃并查看效果

我们尝试将跳跃的速度调快一些，观察其动画表现。同时也发现了一个问题：目前角色似乎可以跳出预定的范围，我们还没有调查具体原因。这部分逻辑还没细看，但从整体表现来看，现在的跳跃已经更接近真实、自然的运动效果。

目前跳跃速度略显偏快，因此后续可能需要对其进行调整。一个思路是把部分跳跃前的动画处理逻辑提前放到"预运动"的阶段执行，也就是说在角色准备起跳的瞬间，头部等部分先做出收缩、压缩的动作，模拟蓄力准备跳跃的感觉。这样，跳跃动作就不是直接开始，而是先有一个动态收缩再弹射的过程，更符合自然运动规律。

如果这么处理，那么我们可能就不再需要做太多基于时间的窗口划分处理，而是让不同的动画状态自然过渡。虽然这部分现在还没实现，但我们先展示了如何通过 T 值分段和窗口映射来完成跳跃动画的初步处理和效果优化。

game_world_mode.cpp：设置 Entity->FacingDirection

接下来我们还需要做的是"Cizek"，不过这里提到的具体内容似乎没有进一步展开。我们可能是要探讨某种差异或需要明确某些操作的不同之处。

在动画或运动处理的上下文中，可能存在着多个技术或方法上的区别，比如不同的动画曲线、不同的状态切换、或是如何在不同阶段进行平滑过渡等。处理这些差异或改进的点，通常会直接影响最终的动画效果和表现。

具体来说，如果是要在跳跃动画中应用某种新的控制方式或是优化现有的代码逻辑，我们可能需要通过更精细的调整、例如在跳跃和落地之间加入新的动态效果，或者通过调整时间步长来获得更自然的运动表现。

通过这种方式，能够使角色的动作更具表现力和真实性，同时也能够解决之前提到的速度过快或是运动范围异常的问题。

B样条和贝塞尔曲线有什么区别？

B样条曲线（B-splines）和贝塞尔曲线（Bezier curves）是计算机图形学和建模中常用的曲线类型。它们都广泛应用于计算机动画、3D建模、图形设计以及工程设计中，具有平滑的性质和灵活的控制能力。接下来详细介绍这两者的特点和使用方式。

贝塞尔曲线（Bezier Curves）

贝塞尔曲线是一类参数化曲线，通常由一组控制点定义。最常见的贝塞尔曲线是二次和三次贝塞尔曲线。

二次贝塞尔曲线：由三个控制点定义，曲线是这些控制点的加权组合。控制点的线性组合形成了曲线的轨迹。
- 二次贝塞尔曲线的公式为：
  
  B ( t ) = ( 1 − t ) 2 P 0 + 2 ( 1 − t ) t P 1 + t 2 P 2 B(t) = (1 - t)^2 P_0 + 2(1 - t) t P_1 + t^2 P_2 B(t)=(1−t)2P0+2(1−t)tP1+t2P2
  
  其中 P 0 , P 1 , P 2 P_0, P_1, P_2 P0,P1,P2 是控制点， t t t 是参数，取值范围从0到1。
三次贝塞尔曲线：由四个控制点定义，具有更高的灵活性，能够表示更加复杂的曲线形状。
- 三次贝塞尔曲线的公式为：
  
  B ( t ) = ( 1 − t ) 3 P 0 + 3 ( 1 − t ) 2 t P 1 + 3 ( 1 − t ) t 2 P 2 + t 3 P 3 B(t) = (1 - t)^3 P_0 + 3(1 - t)^2 t P_1 + 3(1 - t) t^2 P_2 + t^3 P_3 B(t)=(1−t)3P0+3(1−t)2tP1+3(1−t)t2P2+t3P3
  
  其中 P 0 , P 1 , P 2 , P 3 P_0, P_1, P_2, P_3 P0,P1,P2,P3 是控制点， t t t 同样是参数。

贝塞尔曲线的优点是控制点少且直观，适合用来做路径动画和形状建模。贝塞尔曲线具有局部性，即移动一个控制点不会影响曲线的其他部分。

B样条曲线（B-splines）

B样条曲线是贝塞尔曲线的一种扩展，它可以通过多个控制点来定义，具有更强的灵活性。B样条曲线的一个重要特点是它不是由固定数量的控制点定义的，而是由一组控制点和一个节点向量（knot vector）来确定。

控制点：与贝塞尔曲线类似，B样条曲线也有一组控制点，通过这些控制点计算曲线的轨迹。
节点向量：节点向量是一个递增的数列，决定了控制点对曲线的影响范围。通过调整节点向量，可以改变曲线的形状。
局部控制：B样条曲线的一个优势是局部控制。通过调整某个控制点，可以只影响曲线的部分区域，而不会影响整个曲线的形状。
曲线的阶数：B样条曲线的阶数由控制点的数量和节点向量的设置决定。常见的B样条曲线包括二次B样条、三次B样条等。

B样条曲线在建模中非常有用，特别是在需要平滑过渡和灵活控制的情况下。B样条曲线常用于3D建模和CAD系统中，能够表示非常复杂的形状。

比较

贝塞尔曲线适合用少量控制点表示简单的曲线，通常用于图形设计和路径动画。
B样条曲线更适合复杂的建模和需要高自由度的应用，因为它能够通过多个控制点和节点向量提供更大的灵活性和更高的平滑度。

这两种曲线都有广泛的应用，各自有其优缺点，选择哪种曲线取决于具体的需求和使用场景。

二阶贝塞尔.py

py 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib

# 设置 matplotlib 使用非交互式后端以保存动画
matplotlib.use('Agg')

# 配置中文字体
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['SimSun', 'Microsoft YaHei', 'Noto Sans CJK SC', 'Arial']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

def quadratic_bezier(t, P0, P1, P2):
    """计算参数 t 处的二次贝塞尔曲线点"""
    return (1-t)**2 * P0 + 2*(1-t)*t * P1 + t**2 * P2

# 控制点
P0 = np.array([0, 0])
P1 = np.array([1, 2])
P2 = np.array([2, 0])

# 设置图形和坐标轴
fig, ax = plt.subplots(figsize=(8, 6))
ax.set_xlim(-0.5, 2.5)
ax.set_ylim(-0.5, 2.5)
ax.set_xlabel('X轴')
ax.set_ylabel('Y轴')
ax.set_title('二次贝塞尔曲线动画与插值连线')
ax.grid(True)

# 绘制控制点和连线
control_points, = ax.plot([P0[0], P1[0], P2[0]], [P0[1], P1[1], P2[1]], 'ro-', label='控制点')
curve, = ax.plot([], [], 'b-', label='贝塞尔曲线', linewidth=2)
interp_line1, = ax.plot([], [], 'g--', label='控制线')
interp_line2, = ax.plot([], [], 'g--')
interp_point1, = ax.plot([], [], 'go', label='插值点')
interp_point2, = ax.plot([], [], 'go')
interp_connect, = ax.plot([], [], 'm-', label='插值连线', linewidth=1.5)  # 新增连线
moving_point, = ax.plot([], [], 'mo', label='移动点', markersize=10)
ax.legend()

# 曲线数据
t_values = np.linspace(0, 1, 100)
curve_points = np.array([quadratic_bezier(t, P0, P1, P2) for t in t_values])
curve_x, curve_y = [], []

def init():
    """初始化动画"""
    curve.set_data([], [])
    interp_line1.set_data([], [])
    interp_line2.set_data([], [])
    interp_point1.set_data([], [])
    interp_point2.set_data([], [])
    interp_connect.set_data([], [])  # 初始化新增连线
    moving_point.set_data([], [])
    return curve, interp_line1, interp_line2, interp_point1, interp_point2, interp_connect, moving_point

def animate(i):
    """更新第 i 帧的动画"""
    t = t_values[i]
    
    # 更新曲线
    curve_x.append(curve_points[i][0])
    curve_y.append(curve_points[i][1])
    curve.set_data(curve_x, curve_y)
    
    # 计算插值点
    Q0 = (1-t) * P0 + t * P1  # P0 和 P1 之间
    Q1 = (1-t) * P1 + t * P2  # P1 和 P2 之间
    B = quadratic_bezier(t, P0, P1, P2)  # 曲线上的点
    
    # 更新控制线
    interp_line1.set_data([P0[0], P1[0]], [P0[1], P1[1]])
    interp_line2.set_data([P1[0], P2[0]], [P1[1], P2[1]])
    
    # 更新插值点
    interp_point1.set_data([Q0[0]], [Q0[1]])
    interp_point2.set_data([Q1[0]], [Q1[1]])
    
    # 更新插值点之间的连线
    interp_connect.set_data([Q0[0], Q1[0]], [Q0[1], Q1[1]])
    
    # 更新曲线上的移动点
    moving_point.set_data([B[0]], [B[1]])
    
    return curve, interp_line1, interp_line2, interp_point1, interp_point2, interp_connect, moving_point

# 创建动画
ani = FuncAnimation(fig, animate, init_func=init, frames=len(t_values), interval=50, blit=True)

# 保存动画为 GIF
ani.save('bezier_animation_with_interp_line.gif', writer='pillow', fps=20)

# 关闭图形以防止内存问题
plt.close()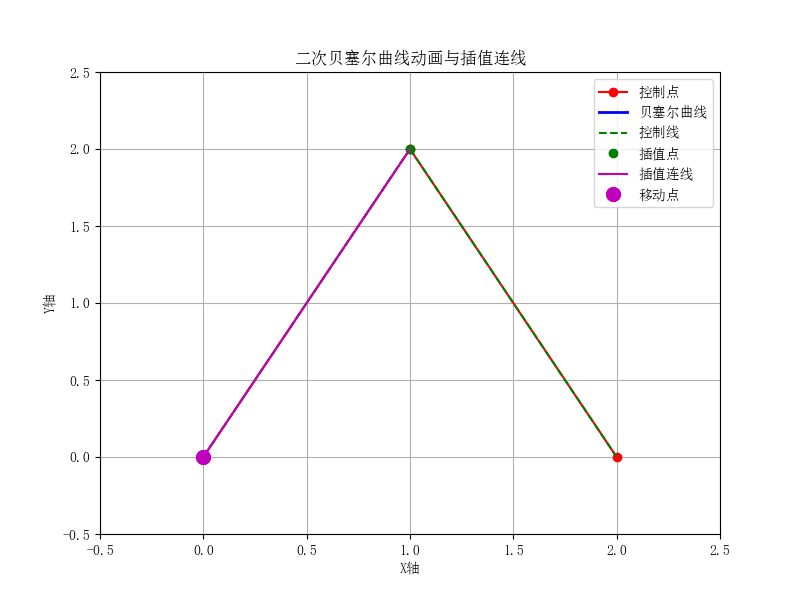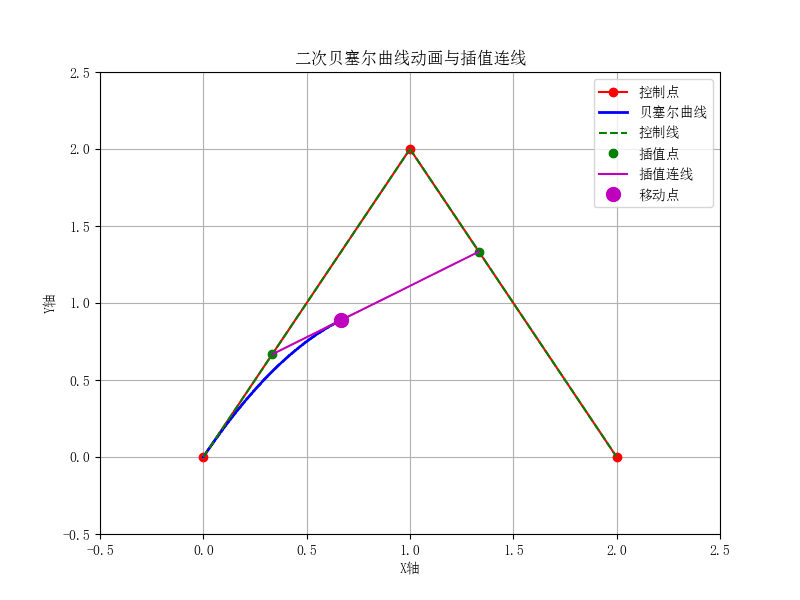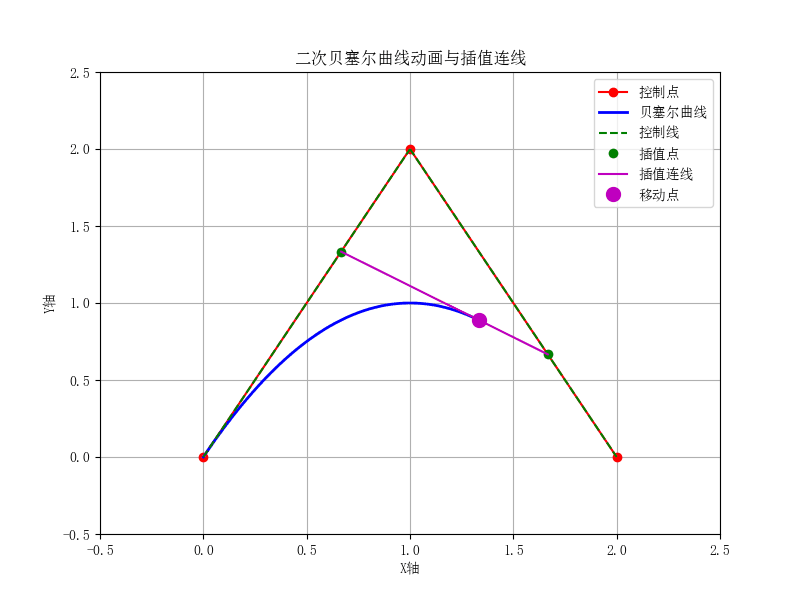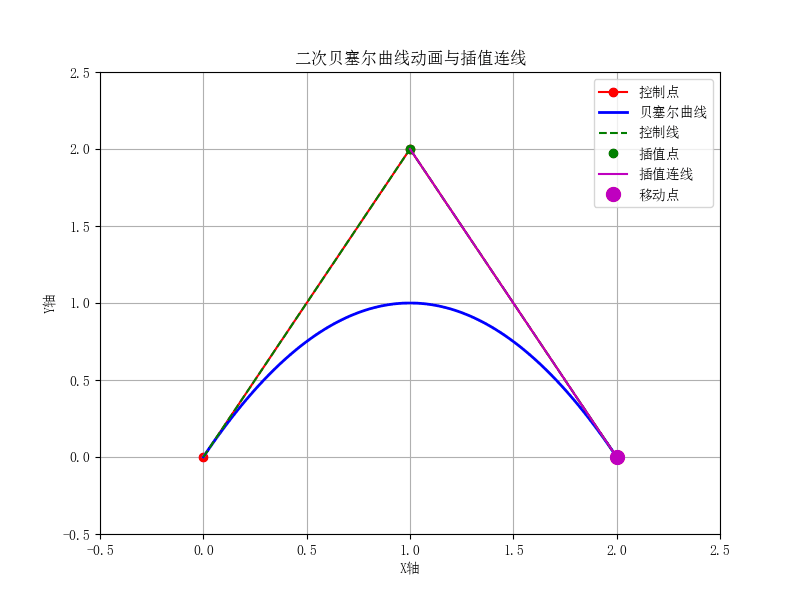

三阶贝塞尔.py

py 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib

# 设置 matplotlib 使用非交互式后端以保存动画
matplotlib.use('Agg')

# 配置中文字体
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['SimSun', 'Microsoft YaHei', 'Noto Sans CJK SC', 'Arial']
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

def cubic_bezier(t, P0, P1, P2, P3):
    """计算参数 t 处的三次贝塞尔曲线点"""
    return (1-t)**3 * P0 + 3*(1-t)**2 * t * P1 + 3*(1-t) * t**2 * P2 + t**3 * P3

# 控制点
P0 = np.array([0, 0])
P1 = np.array([1, 2])
P2 = np.array([2, 0])
P3 = np.array([3, 1])

# 设置图形和坐标轴
fig, ax = plt.subplots(figsize=(8, 6))
ax.set_xlim(-0.5, 3.5)
ax.set_ylim(-0.5, 2.5)
ax.set_xlabel('X轴')
ax.set_ylabel('Y轴')
ax.set_title('三次贝塞尔曲线动画与插值连线')
ax.grid(True)

# 绘制控制点和连线
control_points, = ax.plot([P0[0], P1[0], P2[0], P3[0]], [P0[1], P1[1], P2[1], P3[1]], 'ro-', label='控制点')
curve, = ax.plot([], [], 'b-', label='贝塞尔曲线', linewidth=2)
interp_line1, = ax.plot([], [], 'g--', label='控制线')
interp_line2, = ax.plot([], [], 'g--')
interp_line3, = ax.plot([], [], 'g--')
interp_point1, = ax.plot([], [], 'go', label='一级插值点')
interp_point2, = ax.plot([], [], 'go')
interp_point3, = ax.plot([], [], 'go')
interp_connect1, = ax.plot([], [], 'm-', label='二级插值连线', linewidth=1.5)
interp_connect2, = ax.plot([], [], 'm-', linewidth=1.5)
tertiary_connect, = ax.plot([], [], 'm-', label='三级插值连线', linewidth=1.5)
moving_point, = ax.plot([], [], 'mo', label='移动点', markersize=10)
ax.legend()

# 曲线数据
t_values = np.linspace(0, 1, 100)
curve_points = np.array([cubic_bezier(t, P0, P1, P2, P3) for t in t_values])
curve_x, curve_y = [], []

def init():
    """初始化动画"""
    curve.set_data([], [])
    interp_line1.set_data([], [])
    interp_line2.set_data([], [])
    interp_line3.set_data([], [])
    interp_point1.set_data([], [])
    interp_point2.set_data([], [])
    interp_point3.set_data([], [])
    interp_connect1.set_data([], [])
    interp_connect2.set_data([], [])
    tertiary_connect.set_data([], [])
    moving_point.set_data([], [])
    return curve, interp_line1, interp_line2, interp_line3, interp_point1, interp_point2, interp_point3, interp_connect1, interp_connect2, tertiary_connect, moving_point

def animate(i):
    """更新第 i 帧的动画"""
    t = t_values[i]
    
    # 更新曲线
    curve_x.append(curve_points[i][0])
    curve_y.append(curve_points[i][1])
    curve.set_data(curve_x, curve_y)
    
    # 计算一级插值点
    Q0 = (1-t) * P0 + t * P1  # P0 和 P1 之间
    Q1 = (1-t) * P1 + t * P2  # P1 和 P2 之间
    Q2 = (1-t) * P2 + t * P3  # P2 和 P3 之间
    
    # 计算二级插值点
    R0 = (1-t) * Q0 + t * Q1  # Q0 和 Q1 之间
    R1 = (1-t) * Q1 + t * Q2  # Q1 和 Q2 之间
    
    # 计算曲线上的点
    B = cubic_bezier(t, P0, P1, P2, P3)
    
    # 更新控制线
    interp_line1.set_data([P0[0], P1[0]], [P0[1], P1[1]])
    interp_line2.set_data([P1[0], P2[0]], [P1[1], P2[1]])
    interp_line3.set_data([P2[0], P3[0]], [P2[1], P3[1]])
    
    # 更新一级插值点
    interp_point1.set_data([Q0[0]], [Q0[1]])
    interp_point2.set_data([Q1[0]], [Q1[1]])
    interp_point3.set_data([Q2[0]], [Q2[1]])
    
    # 更新二级插值连线
    interp_connect1.set_data([Q0[0], Q1[0]], [Q0[1], Q1[1]])
    interp_connect2.set_data([Q1[0], Q2[0]], [Q1[1], Q2[1]])
    
    # 更新三级插值连线（仅最新）
    tertiary_connect.set_data([R0[0], R1[0]], [R0[1], R1[1]])
    
    # 更新曲线上的移动点
    moving_point.set_data([B[0]], [B[1]])
    
    return curve, interp_line1, interp_line2, interp_line3, interp_point1, interp_point2, interp_point3, interp_connect1, interp_connect2, tertiary_connect, moving_point

# 创建动画
ani = FuncAnimation(fig, animate, init_func=init, frames=len(t_values), interval=50, blit=True)

# 保存动画为 GIF
ani.save('cubic_bezier_animation.gif', writer='pillow', fps=20)

# 关闭图形以防止内存问题
plt.close()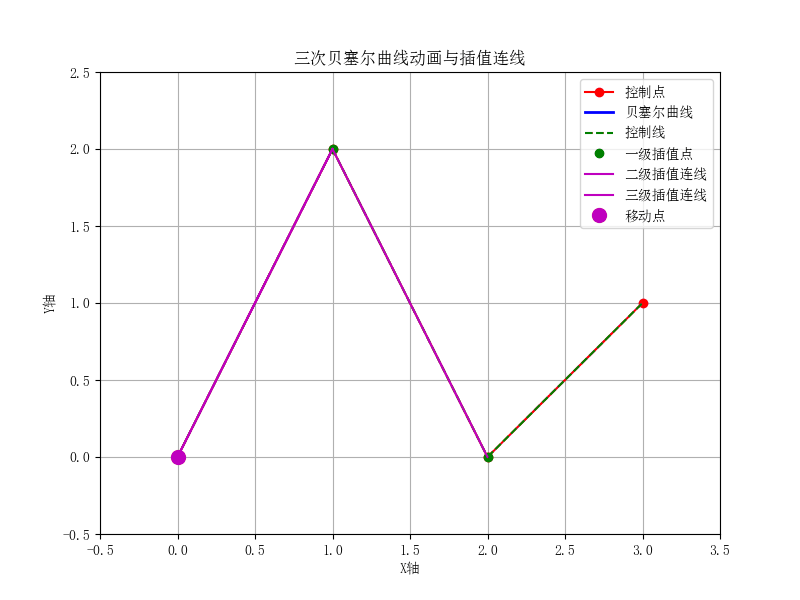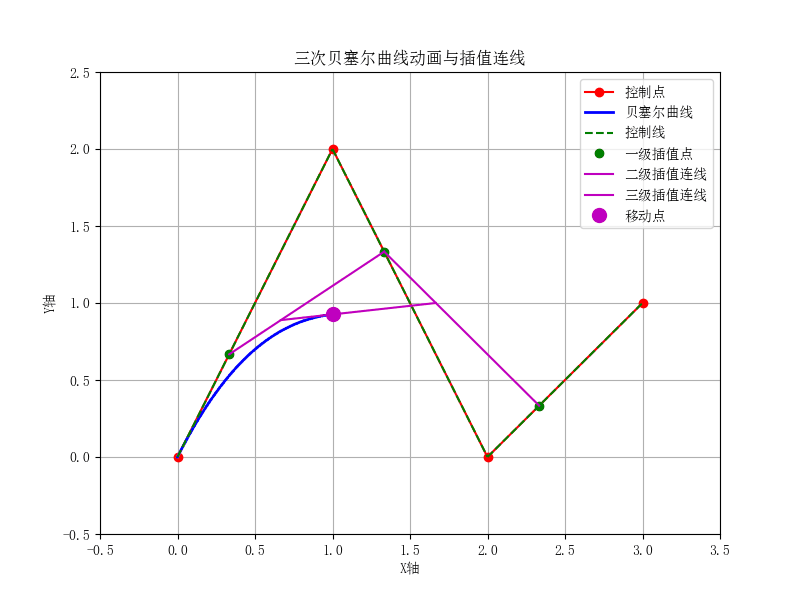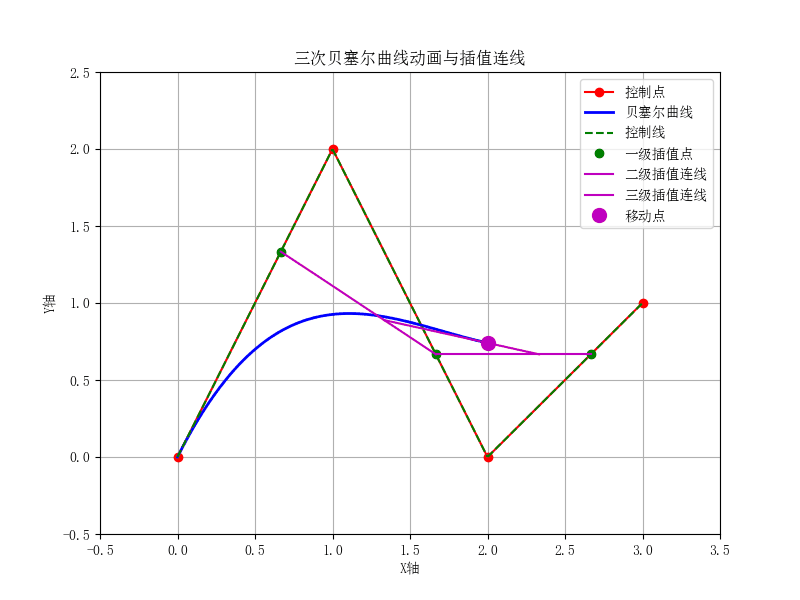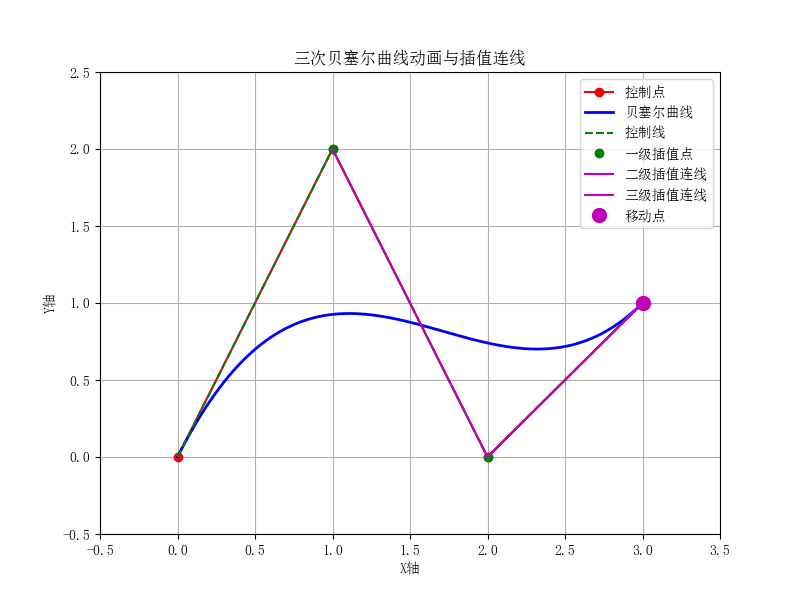

黑板：贝塞尔曲线与B样条曲线

贝塞尔曲线（Bezier curves）和B样条曲线（B-splines）实际上可以产生相同的曲线，二者的主要区别在于"节点"或"控制点"的使用方式。尽管这两种曲线在形式上没有差别，但它们在如何组织和定义控制点方面有所不同，尤其是在节点（knots）和控制点（control points）的表示方法上。

贝塞尔曲线（Bezier Curves）与B样条曲线（B-Splines）的区别：

控制点和节点的关系：
- 贝塞尔曲线：在贝塞尔曲线中，控制点直接定义了曲线的形状。每个控制点都对应着曲线上的一个位置，且整个曲线由控制点的组合生成。贝塞尔曲线的控制点是顺序排列的，曲线的形状依赖于这些点的排列和个数。
- B样条曲线：在B样条曲线中，"节点"与控制点是分开的。节点定义了曲线中控制点影响的区域。节点向量控制着每个控制点如何影响曲线的不同部分，而控制点本身决定曲线的形状和位置。B样条曲线通过调整节点向量来提供更多的灵活性。
节点与控制点的定义：
- 贝塞尔曲线的控制点和"t值"（即节点）之间是直接相关的，节点实际上代表了控制点在曲线上的位置。贝塞尔曲线没有单独的节点向量，只有一组控制点，曲线的形状由这些控制点的排列决定。
- B样条曲线则通过节点向量来调整控制点的影响范围。节点向量通常是递增的，它决定了哪些控制点在曲线的不同区域中起作用。节点的选择对曲线的形状和光滑度有很大影响。
平滑度和局部控制：
- 贝塞尔曲线的平滑度较低，尤其是控制点较少时，它适合简单的曲线表示，但在复杂曲线建模时，贝塞尔曲线可能不如B样条灵活。
- B样条曲线通过控制节点向量和多个控制点的组合，能够提供更高的平滑度和灵活性。它支持局部控制，即改变一个控制点只影响曲线的一部分，而不会影响整个曲线。
曲线阶数：
- 贝塞尔曲线的阶数通常是固定的，常见的有二次和三次贝塞尔曲线。
- B样条曲线的阶数可以根据控制点和节点的数量灵活调整，可以是二次、三次甚至更高阶的。

总结：

虽然贝塞尔曲线和B样条曲线在数学上可以产生相同的曲线形状，二者的区别主要体现在如何定义和使用控制点和节点。贝塞尔曲线将控制点直接与曲线相关联，而B样条曲线则通过节点向量灵活地控制曲线的形状和光滑度。两者的选择取决于具体应用的需要，比如贝塞尔曲线适合简单的路径或形状表示，而B样条曲线更适合复杂建模和需要高灵活度的情况。

黑板：贝塞尔曲线

当我们讨论贝塞尔曲线（Bezier curves）与B样条曲线（B-splines）时，关键的区别在于它们如何处理控制点和曲线的连续性。我们以一个例子来说明贝塞尔曲线的工作原理。

贝塞尔曲线和B样条曲线的区别：

贝塞尔曲线：贝塞尔曲线的一个重要特点是它是一个固定的曲线，控制点的数量等于曲线阶数加一。例如，对于一个三阶贝塞尔曲线（通常使用），它有四个控制点。每个贝塞尔曲线段的控制点数是固定的，且与阶数密切相关。对于一个三阶贝塞尔曲线，控制点是4个，分别对应曲线的起始点、结束点和两个控制点。通过调整这些控制点，可以改变曲线的形状。
多个贝塞尔曲线连接：当需要将多个贝塞尔曲线连接成一个连续的曲线时，我们需要确保连接点的切线（即控制点）是对齐的。为了实现这一点：
- 连接两条贝塞尔曲线时，控制点之间必须满足对称关系。具体来说，连接点前一个控制点的切线控制点应当与下一条贝塞尔曲线起始点的控制点相对，并且二者的长度应该相同。
- 数学上，假设有三个点 A、B、C，则 A-B 与 C-B 的向量必须是对称的，即 A-B = -(C-B)，这意味着它们的方向是相反的，且长度相等。
连续性要求：要保证贝塞尔曲线在连接处是平滑的（即连续的），必须遵守上述规则。如果不遵守这些规则，连接处就会出现折线（kink）或者不平滑的转折。为了避免这种情况，在画图软件中，通常可以锁定控制点的切线方向，防止它们被不适当地调整，从而破坏曲线的平滑性。
曲线的加速度和方向：
- 如果连接两条贝塞尔曲线时，两个控制点的方向一致，但加速度不同，那么连接点处的曲线仍然是平滑的，但会出现一些二阶变化。这意味着曲线的方向是平滑变化的，但它的弯曲速度（即加速度）有所不同，表现为曲线的弯曲程度不同。

总结：

贝塞尔曲线是通过一系列的控制点来定义的，每个控制点都影响曲线的一部分。为了使多条贝塞尔曲线连接成一个平滑的曲线，我们需要确保它们的连接点的切线是对称且等长的。贝塞尔曲线适合用于简单的、逐段连接的曲线建模，但需要小心控制点之间的关系，以保持曲线的平滑性和连续性。

黑板：B样条曲线

B样条（B-spline）和贝塞尔曲线（Bezier curve）在数学上产生的曲线是相同的，但它们的控制方式和操作过程有所不同。下面详细解释两者的差异：

贝塞尔曲线和B样条的对比：

贝塞尔曲线：
- 贝塞尔曲线是固定的曲线，其控制点的数量等于曲线的阶数加一。例如，对于一个三阶贝塞尔曲线（常见的类型），有四个控制点。
- 在贝塞尔曲线中，曲线是从第一个控制点到最后一个控制点的直线段，经过所有控制点并且最终落在最后一个控制点上。
- 如果想要将多个贝塞尔曲线连接起来，必须确保相邻曲线的连接点切线方向相同且长度相等。否则，曲线连接处会出现不平滑的拐角。
B样条曲线：
- 与贝塞尔曲线不同，B样条曲线不要求每个控制点都被曲线经过。B样条是一种更加灵活的曲线，它可以通过控制点的集合来确定曲线的形状，但曲线本身不会直接穿过这些控制点，除非在曲线的端点。
- 在B样条中，控制点影响的是曲线的形状，而不是直接决定曲线的路径。B样条曲线更像是"滑动"通过所有控制点，曲线只会在最后的控制点上与其相交。
- 通过增加控制点的数量，B样条可以产生一个复杂的曲线，而不会因为添加更多控制点而使得每个控制点都被曲线所通过。
B样条的计算：
- B样条曲线通过事先解决控制点和节点的问题来生成曲线。它使用了一种类似贝塞尔曲线的数学结构，但不同之处在于，B样条会在每个时间段内依次使用不同的控制点来计算曲线，而不直接固定在一个控制点上。这种方式确保了曲线在经过每一段时不断调整，直到最终到达最后一个控制点。
- B样条的优点是，它可以处理更多的控制点，并且保持曲线的平滑性和连续性，不会像贝塞尔曲线那样受到控制点过多的影响。
相同的曲线表达：
- 虽然贝塞尔曲线和B样条曲线的定义不同，但它们生成的曲线是相同的。两者实际上是相同的数学方程，只是处理和控制曲线的方式不同。通过合适的控制点设置，贝塞尔曲线和B样条曲线可以生成完全相同的曲线。
- 也就是说，虽然控制点的方式不同，但通过合理选择控制点，可以使得贝塞尔曲线和B样条曲线产生相同的效果。

总结：

贝塞尔曲线和B样条曲线的主要区别在于它们如何使用控制点和如何计算曲线。贝塞尔曲线通过直接控制曲线的路径并要求曲线经过所有控制点，而B样条曲线则通过控制点来影响曲线的形状，但不会直接经过这些控制点，直到最后的一个控制点。尽管两者的控制方式不同，但它们所生成的曲线是相同的。

从初学者的角度来看，在软件渲染中，保持"每帧毫秒数"在一定控制范围内在程序员的掌控之中（取决于代码质量和性能导向）。进入硬件渲染（包括驱动程序）时会变得更困难吗？还是相反？

从初学者的角度来看，在软件渲染中，保持每帧的毫秒数在一个受控的范围内，通常是依赖于程序的代码质量和性能优化。当切换到硬件渲染时，是否会变得更加困难，特别是在驱动程序层面的问题，实际上两者的难度是相似的。

软件渲染的挑战：
- 在软件渲染中，程序员需要在不同的CPU上进行优化。由于不同的CPU具有不同的性能和架构，无法预测程序在所有系统上都能表现一致。这使得确保每帧的渲染时间控制在一定范围内变得更加困难。
硬件渲染的挑战：
- 在硬件渲染中，挑战同样存在，因为不同的GPU也具有不同的架构和性能。有些GPU的性能可能较差，或者驱动程序的优化不够好，这会导致在某些硬件上渲染效果无法控制或不稳定。
- 由于硬件和驱动程序的差异，开发者无法确定程序在每一台机器上都会有相同的表现，这给硬件渲染带来了不小的挑战。
硬件一致性的优势（如控制台）：
- 在游戏开发中，许多人喜欢开发主机游戏，因为主机通常只有一个固定的硬件配置。这意味着，开发者知道硬件的具体性能和特点，可以根据这些信息来优化代码，确保性能和表现的一致性。相较于PC，主机上的硬件和驱动程序配置不会变化，因此开发者无需担心在不同硬件或驱动上遇到不确定的性能问题。

总的来说，无论是软件渲染还是硬件渲染，都面临着不同硬件配置带来的挑战，尤其是在PC上，由于硬件种类繁多，开发者很难做到在所有机器上都达到理想的表现。这也是为什么开发者更倾向于在主机上开发，因为硬件环境更加可控。

我们会对图像进行压缩，还是只是移动躯干？

在处理图像时，可能需要对画面进行压缩，或者只是调整躯干的运动。为了让披风能够准确地覆盖到头部，必须将披风拉伸至两倍长度。这个操作是不可避免的，因为披风需要适应躯干的运动和位置变化，从而保持自然的效果。

什么样的游戏设计决策需要使用跳跃/瓷砖跳跃，而不是之前的英雄移动方式？

关于游戏设计的讨论没有被涉及，因此选择跳过了这一部分内容。

是否可以创建像《乐一通》那样的动画，在静止的画面中可以看到多个头部、四肢或极度夸张和扭曲的特征？尽管如此，运动中看起来依然正常。我查到"拖尾动画"这一术语

可以通过使用多个静态帧来创建像《乐一通》那样的动画，尽管其中的头部、四肢或其他特征可能会极度夸张和扭曲，但在运动中依然看起来很自然。这样的效果通常被称为"拖影动画"（Smear Animation）。这种技术的核心是通过快速绘制多个帧，使得角色或物体的动作看起来更加生动、富有表现力，并且能传达夸张的动作感。

关于选择使用Java还是C语言的问题，虽然没有深入探讨，但在某些情况下，C语言可能更适合，因为它的执行效率更高，尤其是在需要进行低级操作或对性能要求较高的项目中。而Java则通常用于跨平台应用和更高层次的抽象。

为什么不使用Java，而是C语言？

在专业的3D游戏引擎中，几乎没有使用Java编写的。举例来说，像Frostbite、Unreal、Unity、Destiny等知名引擎都是使用C++或其他语言编写的，而不是Java。所以，如果目标是进入游戏引擎编程领域并希望在一个引擎团队工作，仅掌握Java编程语言是无法胜任的。

虽然可以用Java编写一些小型游戏，或者进行游戏原型开发，但对于高端游戏引擎编程，Java并不适合。甚至很多游戏（包括《Minecraft》）虽然使用了Java，但由于性能较差，因此不被视为高端的游戏开发选择。大多数现代游戏更倾向于使用C#，特别是在使用Unity引擎时，C#几乎是唯一的编程语言选择。

对于游戏编程，如果打算在引擎开发和性能优化方面有所成就，C#和C++更为常见和受欢迎。而Java的使用范围主要局限在Android移动游戏等平台，因为Android本身是基于Java的。但即使如此，Java并不适用于开发高性能的游戏引擎。

总之，Java并不是游戏引擎编程的首选语言，也不是行业中的主流。

Jmonkey 和 LWJGL 是一些用Java编写的专业开源库，仅举几个例子

Java并不是主流的游戏引擎开发语言，许多游戏引擎都没有使用Java。尽管有一些使用Java的游戏引擎，但它们通常是小型或实验性的引擎，而不是真正的高性能游戏引擎。即使是一些在Steam上排名前50的游戏，其使用的引擎也绝对不是用Java编写的。如果目标是进入一家游戏公司从事引擎开发工作，使用Java的机会几乎是不存在的。

Java游戏引擎更多地被视为"玩具级"工具，而非用于制作大型游戏的工具。例如，一些小型游戏公司或开发者可能使用Java开发游戏，但这些游戏通常不属于主流或高性能游戏。相比之下，C#在游戏开发中更为常见，尤其是在Unity引擎中，C#是主要的编程语言。此外，还有一些游戏曾使用过XNA框架（如《Bastion》和《Fez》），但这些框架也并不是Java。

总的来说，如果想从事游戏引擎开发，Java并不是一个实用的选择，而C++和C#才是更为常见的主流语言。

为了将身体拉伸到头部，我们是否会在SE中实现剪切变换？

理想的游戏编程通常包括几项关键特点：

高效性：游戏编程需要确保代码执行高效，能够处理复杂的游戏逻辑和图形渲染，特别是在硬件性能不同的设备上。
模块化和可扩展性：理想的游戏编程会重视模块化的设计，这样可以使得游戏的各个部分能够独立开发和更新，便于后期的扩展和维护。
流畅的动画和物理模拟：游戏中的动画和物理效果需要做到流畅和真实，这涉及到复杂的计算和精细的控制，确保游戏在视觉上吸引人。
跨平台兼容性：理想的编程应该确保游戏可以在多个平台上运行，如PC、主机、手机等，尽量减少平台间的差异。
易于调试和测试：理想的编程还需要方便调试，能够在开发过程中快速检测并修复bug。
与团队协作：游戏开发是一个团队合作的过程，因此理想的游戏编程方式应该支持多人协作开发，代码管理工具（如Git）和良好的文档化是必须的。

这些特点帮助游戏程序员在开发过程中解决技术难题，同时保持游戏的稳定性和玩家体验。

你理想中的游戏编程语言是什么样的？

关于语言和元编程，这些语言通常是非常注重元编程特性的。元编程指的是能够编写能操控代码本身的程序代码。这种编程方式允许开发者通过程序动态地创建、修改或优化代码结构。它为开发人员提供了极大的灵活性，使得某些复杂的任务可以通过代码自动化处理，而不是手动编写大量重复的代码。

在元编程中，程序能够读取、分析、生成或修改自身的代码，这使得它能够在运行时作出更复杂的决策或自我优化。许多现代编程语言都支持某种形式的元编程，但某些语言在这方面更为强大或灵活，例如Lisp和Ruby。

你看过关于Ubi的Rayman 2D动画编辑器的视频吗？

提到的Rayman 2D动画编辑器似乎是一个功能非常复杂的工具，可能包含很多按钮和选项，需要花时间去熟悉和掌握。虽然一开始看起来有点令人困惑，但如果深入了解它的功能和使用方式，应该能够更加得心应手。这样的编辑器可能包含了许多动画编辑的功能，比如帧管理、时间轴控制、插值等，可以帮助制作流畅且富有表现力的2D动画。

对于刚接触的人来说，面对复杂的界面和众多的按钮可能会感觉有些困难，但是通过逐步的学习和实践，应该能够掌握并且发挥它的强大功能。

动画功能最终会被移出来，让其他实体也能使用吗？

最终目标是让其他实体也能使用这些功能。这意味着系统或功能会被设计成可复用的，使得不同的实体可以方便地调用和利用这些功能。这种设计方式不仅提高了效率，还确保了代码的模块化和可维护性。通过将功能模块化，其他部分的代码可以在需要时直接访问这些功能，而不需要重新实现或复制相同的逻辑，从而减少了冗余和错误的发生。

将矢量图和光栅图结合在游戏中使用，是否推荐？

是否在游戏中混合使用矢量图形和光栅图形取决于具体的情况。虽然没有理由不能将两者结合使用，但是否适合要根据具体的需求和情况来决定。矢量图形通常适合需要缩放和清晰度保持一致的场景，而光栅图形则更适合具有复杂细节的静态或动态图像。因此，选择是否混合使用这两种图形技术，需要综合考虑游戏的风格、性能要求和艺术设计目标等因素。

David Rosen 在Wolfire的GDC演讲中谈到了程序化动画。你看过吗？如果看过，有什么想法？ $$见资源：Wolfire Blog]

在关于"页面动画"的GDC讲座中，内容总体来说是不错的。不过，在观察到的《Overgrowth》中的动画效果时，感觉它的表现有些问题。尽管讲者提到了一些技术和方法，但从实际效果来看，我认为动画应该比展示的效果更好。可能的原因是使用的动画采样不够充分，导致动画的流畅性和细节表现不足。

具体来说，可能是对速度的处理不够精确，导致动画的加速度或变化不够平滑，表现出一些不连续性，特别是在二阶导数的变化上。这种不平滑的过渡使得动画看起来不够自然。因此，虽然讲者描述的技术原理听起来很好，但在实现过程中似乎遇到了一些问题，导致实际效果没有达到预期。

当然，《Overgrowth》这款游戏还没有正式发布，可能开发团队对这些问题已经有所意识，并计划在后续更新中修复这些问题，因此这些问题可能在最终版本中得到解决。

人类距离编程出我们的宇宙的仿真有多远？

这个问题涉及到人类与编程效果的关系以及如何理解宇宙的主导作用。可以从编程的角度来看待：编程是创建和控制数字世界的一种工具，类似于人类在探索和创造虚拟世界中的"主导力量"。然而，宇宙本身的"编程"或"主导"则更为复杂，它涉及到自然法则、物理定律等不可人为控制的因素。

从编程效果的角度来看，编程是通过语言和逻辑控制计算机的行为，类似于对某些过程的编制和操控。人类通过编程探索虚拟世界，并赋予它们生命。然而，与宇宙的广阔无垠和复杂性相比，编程只能在有限的规则和框架内进行创造。宇宙的运行和规律不是由单一的指令或逻辑控制的，而是由深层次的物理规律和自然力量主导的，这些力量超越了人类的能力范畴。

简而言之，人类的编程和宇宙的运作各自有其不同的性质，一个是人为设计的系统，而另一个是自然的、无法完全控制的宏大系统。

对于那些认为Java在某些情况下比C++更快的研究者，你怎么看？

有些研究人员声称，Java在某些情况下可能比C++更快。针对这种说法，经过深入分析后发现，通常他们的结论是不正确的。即使这些研究者提供了一些数据，仔细研究后，发现他们的方法和结论都是不合理的，因为从技术角度来看，Java不可能在性能上超过C++。许多时候，这些研究者其实并不是在说Java在整体上比C++更快，而是说如果你以某种特定方式编写程序，并使用Java的特定构造，而C++使用不同的构造，那么在这种特定场景下，Java可能会比C++更快。然而，这种情况实际上是没有实际意义的，因为任何开发者都可以使用C++以更高效的方式来实现相同的功能，而不需要依赖于特定的编程构造。

有时，Java的编译器可能会针对某些特定情况进行优化，而C++可能会有一些性能瓶颈。例如，LLVM（低级虚拟机）在某些方面可能会表现得较慢，导致C++在某些任务上的性能不如Java，但这并不是Java整体优于C++的证据。总的来说，这类说法的实质问题在于它们通常无法证明Java在更广泛的应用场景中会比C++更快。

很棒，另外，关于元编程，你看过Per Vognsen的btree元编程吗？显然它复制了Jeff Roberts的AVL树可配置性方案

没有，我们还没有看到相关内容。

Runescape 是一款基于浏览器的MMO

我们提到RuneScape是一个图形化的浏览器游戏，客户端是用Java编写的。这可能听起来不错，但它并不被认为是"严肃"的游戏类型。事实上，这个游戏最近刚刚发布了一个C++版本的客户端，也就是说他们选择用更高性能的语言替代了Java实现，说明原本的Java客户端已经不再满足需求。

从这个例子来看，如果我们想开发高性能的游戏，尤其是专业级别的引擎或大型3D游戏，Java并不是一个合适的选择。即使是像Minecraft这样广为人知的游戏，其Java实现在性能方面也一直饱受批评。因此，如果目标是进入专业游戏开发行业，特别是从事游戏引擎开发，掌握C++是几乎必不可少的。

当然，如果只是想做一些简单的游戏原型或是非商业的爱好项目，使用Java或者其他任何语言都没问题，但它们在游戏行业中的应用范围和深度非常有限。选择编程语言时应该考虑目标平台、性能需求、行业通用性以及可获得的开发资源等因素。

问：我以为Minecraft已经移植到C++了

我们讨论是否有将某个项目（可能是指Minecraft）移植到C++的问题。虽然有人建议它已经被移植了，但我们对此表示怀疑。如果真的已经完成了这样重要的移植，按理来说应该有公开的官方宣布才对。或许是微软完成了移植，但目前没有确凿的信息可以证明这一点，因此我们认为暂时还没有看到明确的证据说明该项目已经被完整移植到C++。

Win10版是C++

目前曾使用 Java 开发的一些著名游戏，已经被重新用 C++ 重写或移植。例如，Minecraft 最初是使用 Java 编写的，但后来推出了使用 C++ 开发的版本，即所谓的基岩版（Bedrock Edition），以更好地在多平台（尤其是主机和移动设备）上运行。Runescape 也经历了类似的过程，早期版本使用 Java 实现，但后来为了性能优化和更好的平台支持，也被移植到了 C++ 实现的客户端。

这些变化反映出一个趋势：虽然 Java 曾被用于某些游戏开发，但在追求更高性能、更广泛平台兼容性和更低层系统控制的需求下，最终这些项目都选择转向了 C++。这种转变说明了 Java 在高性能游戏开发中的局限性，以及 C++ 在底层资源控制和优化方面的优势。最终结果是，那些原本用 Java 开发的知名游戏，如今主流版本都是用 C++ 重写的。

游戏引擎学习第273天:动画预览

回顾并为一天的内容定下基调

黑板：动画

黑板：曝光时间和时间间隔

1. 运动模糊的物理原因

2. 轨迹效果的物理原因

3. 滚转快门效应的物理原因

4. 光学与镜头的影响

5. 总结

黑板：瞬时动画

1. 瞬间动画和"黑客"解决方案

2. 游戏中的动画采样

3. 灵活的时间步长

4. 动画函数的设计

5. 基于时间的动画更新

黑板：使用欧拉步长进行数值积分以计算瞬时动画

1. 显式函数与增量更新

2. 数值积分：前向欧拉法

3. 前向欧拉法的局限

4. 复杂动画的挑战

5. 实际应用中的问题

6. 总结

黑板：许多关于时间 t 的函数

1. 时间变量与动画

2. 时间的传递与更新

3. 欧拉法与数值更新

4. 动画的分离与组合

5. 总结

黑板：物理学与动画

黑板：动画技术：B样条和欧拉角

黑板：B样条的阶数

1. 0阶 B 样条（Step Function）

2. 1阶 B 样条（线性插值）

3. 2阶 B 样条（抛物线）

4. 3阶 B 样条（立方曲线）

样条曲线的结构组成：

样条曲线的统一性与兼容性：

样条曲线不是唯一选择：

总结：

黑板：参数空间、状态向量和广义坐标

游戏中我们关注的"状态"是什么？

动画状态的参数化：我们自由决定状态向量的形式

这不是骨骼动画系统 ------ 但功能上更高效

状态向量是动画的核心

动画系统如何使用状态向量？

总结核心思维方式：

黑板："位置向量"与"状态向量"

状态向量与位置向量的区别与关系

状态向量（State Vector）

位置向量（Position Vector）

动画的更新流程

补充概念：广义坐标（Generalized Coordinates）

命名上的小讨论

总结

黑板：动画管线：存储 -> 渲染输入 -> 精灵列表

第一阶段：存储的数据（Stored Data）

第二阶段：渲染输入（Render Input）

第三阶段：渲染生成（Render Output）

总结：完整流程结构

黑板："骨骼动画"

骨骼系统的核心思想

每个骨骼包含的标准属性

系统的规范化 vs 灵活性的折衷

总结：骨骼系统在动画架构中的定位

黑板：渲染动画

举例说明：角色跳跃的动画系统

基础动画 vs 专业级动画的差异

改进方向

后续计划

网络：生命的幻觉：迪士尼动画1 《生命的幻象：迪斯尼动画造型设计》 好像是叫这个

动画从业者必须掌握的基础知识

理解动画：不仅仅是代码问题

编程实现只是传达的手段

小结

黑板：预期和跟随

当前实现存在的问题

Anticipation（预备动作）

动画增强的需求

技术思路：时间窗口分区（T分段）

实现策略

网络：生命的幻觉：迪士尼动画1 《生命的幻象：迪斯尼动画造型设计》好像是叫这个